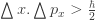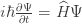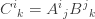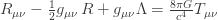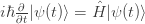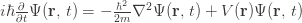Nguyễn Phương Văn's Blog, page 10

Hội An, Kẻ Chàm, Nước Mặn

(Bài này chỉ là một bản tóm tắt theo dòng thời gian một vài tư liệu chính, còn các văn bản gốc, tức ảnh chụp từ lưu trữ văn khố bên Nhà Mẹ ở Rome, thực ra rất khó đọc, khó đoán, nhất là các văn bản viết tay chữ lí nhí, mờ tịt, câu văn thì không có chấm phảy như tiếng Việt hiện nay, đọc cũng rất khó hiểu).

Hội An (Hải Phố) thời đầu những năm 1600, nói theo ngôn ngữ bây giờ, là một đặc khu cả về hành chính lẫn kinh tế của nước Đàng Trong. “Phố Biển” này là một thương cảng rất quan trọng để kết nối Macau, Nagasaki (Nhật) và Malacca.

Chúa Tiên Nguyễn Hoàng thành lập dinh trấn Quảng Nam vào khoảng năm 1602 và cử hoàng tử thứ sáu là Nguyễn Phúc Nguyên làm trấn thủ dinh này. Khi Nguyễn Phúc Nguyên lên ngôi “Chúa”, ông cử con trai mình là Nguyễn Phúc Kỳ làm trấn thủ dinh Quảng Nam. Như vậy, với nước Đàng Trong khi ấy, Quảng Nam chắc chắn có vai trò cực kỳ quan trọng, tương đương vai trò của Sài Gòn với Việt Nam bây giờ.

Đặc khu Hội An có hai khu phố buôn, của người Nhật (phố Nhật), và của người Hoa (phố Khách). Chúa Nguyễn giao quyền cai trị (trưởng phố) khu người Nhật cho một thương gia Nhật, và trao khu người Hoa cho một thương gia Hoa. Các thương gia Bồ Đào Nha, Hà Lan, Tây Ban Nha cũng được giao cho người Nhật quản lý.

Kém quan trọng hơn Hội An một chút là thương cảng Cửa Hàn và Nước Mặn.

*

Cuối những năm 1500, các dòng Phan Sinh (Franciscan), dòng Đa Minh (Dominican), và dòng Âu Tinh (Augustine) đã vào Đàng Trong thông qua các cửa biển Cần Cạo (Hà Tiên), Cửa Hàn (Đà Nẵng). Họ đến Hà Tiên chỉ để đi qua đất Cambodia, hoặc đến Cửa Hàn để phục vụ thương nhân ngoại quốc ở Đàng Trong. Giai đoạn này họ chưa quan tâm nhiều đến việc truyền giáo cho người bản xứ.

Khoảng năm 1614, ở Nhật bắt đầu cấm đạo và bế quan, thương gia và dân có đạo ở Nhật chuyển đến Hội An. Các linh mục truyền giáo của Dòng Tên, bắt đầu di chuyển qua lại giữa Macao/Malacca, Hội An và Nhật Bản. Do tuyến đường đi từ Malacca (nơi Dòng Tên, do vua Bồ Đào Nha bảo trợ, đặt trụ sở để phục vụ truyền giáo tới Nhật Bản) bị Nhật kiểm soát chặt chẽ.

Linh mục Francesco Buzomi, sinh năm 1576 ở Napoli, bị trục xuất khỏi Nhật, về Tỉnh dòng của Dòng Tên đặt ở Macao (Áo Môn) làm giáo sư thần học, rồi được cử đến Hội An năm 1615. Sứ vụ của ông ở vùng này (Quảng Nam và Quy Nhơn) bất ngờ có những tiến triển tích cực, nên Tỉnh Dòng cử thêm linh mục Francisco de Pina sang trợ giúp.

Linh mục Pina là người đặt viên móng đầu tiên cho việc thiết kế và tạo tác chữ quốc ngữ, mà chúng ta đang dùng ngày nay: ông là người đưa các ký tự abc vào trong tiếng Việt.

*

Francisco de Pina, sinh 1585 ở Bồ Đào Nha, tới Đàng Trong năm 1617, ở Hội An năm 1618. Năm 1623 ông đến Kẻ Chàm (tức Thanh Chiêm)  là thủ phủ của Quảng Nam. Ông chết đuối trên biển ở đây năm 1625.

Những năm này, trong các linh mục Dòng Tên đến Hội An còn có các linh mục người Nhật. Trong đó có Pedro Marques (1575-1670), bố người Bồ Đào Nha, mẹ người Nhật. Linh mục Marques không chỉ tham gia truyền giáo tới người Việt ở Đàng Trong mà còn làm sứ vụ này ở đảo Hải Nam. Ngoài ra còn có các thầy tu người Nhật đi cùng, mà không rõ tên thật, tài liệu chỉ chép tên thánh là Joseph và Paulus Saito. Thầy Saito sau đi ra Đàng Ngoài cùng linh mục Gaspar d’Amaral quãng năm 1629-1630.

Các linh mục và thầy tu người Nhật là cầu nối rất quan trọng để các linh mục Dòng Tên hội nhập vào cộng đồng thương gia Nhật ở Hội An, mở rộng quan hệ qua quan chức của chúa Nguyễn, học tiếng Việt và tìm hiểu văn hóa Việt Nam.

Chúa Nguyễn Hoàng trong thập niên đầu tiên của 1600 có quan hệ tốt với Nhật. Ông có trao đổi thư từ với Tokugawa trong nhiều năm. Ông nhận phái viên thương mại của Tokugawa là Hunamoto làm con nuôi. Khi hoàng tử Nguyễn Phúc Nguyên lên thay Chúa Nguyễn Hoàng, ông gả nghĩa nữ (con gái nuôi) cho thương gia kiêm trưởng phố Nhật là Araki Sotaro, qua đó nhận vị Nhật kiều gốc gác samurai này vào hoàng tộc nhà Nguyễn. Buzomi và Pina có quan hệ rất tốt với quan trấn thủ Quảng Nam lúc đó là hoàng tử Nguyễn Phúc Kỳ, và từ đây và ở đây chữ quốc ngữ ra đời.

Linh mục Pina là người giỏi (nói) tiếng Việt nhất, hiểu người Việt nhất và quảng giao nhất. Nhờ vậy ông kết thân được với giới thượng lưu ở Quảng Nam.

Để giảng đạo cho người bản xứ, Pina soạn sách giáo lý theo tiếng Việt, hồi đó họ gọi là tiếng Đàng Trong, rồi dùng ký tự Latin để viết thành bài giảng theo âm đọc tiếng Việt. Các linh mục chép tay cuốn sách này rồi cầm lên đọc lúc giảng kinh. Cách viết ấy, đại khái giống như cách ta viết âm tiếng Anh kiểu báo Nhân Dân: hê-lô, đô-la, uôn-cúp, đô-nan-trum. Các sách này cũng được chép qua chữ nôm để dùng cho giáo dân.

[image error]

(Ai thuộc kinh Lạy Cha, có thể đoán được đoạn ký tự rắc rối, vốn là chữ quốc ngữ sơ khai ở trên. Ví dụ hai câu đầu: Cha chúng tôi ở trên trời [tlên blời] chúng tôi nguyện danh Cha cả sáng. Nước Cha trị đến. Hoặc hai câu cuối: Chẳng được để chúng tôi sa cám dỗ. Bèn cứu chúng tôi trước sự dữ”). 

Việc dùng ký tự Latin để ký âm tiếng địa phương theo cách này, không quá xa lạ với các nhà truyền giáo, nhất là khi họ được các linh mục gốc Nhật vốn có kinh nghiệm trong việc la tinh hóa tiếng Nhật và tiếng Hoa.

Cho tới quãng 1620, Dòng Tên ở Đàng Trong đã có hai cơ sở (họ gọi là cư sở) rất vững chắc ở Nước Mặn (Quy Nhơn) và Kẻ Chàm (Quảng Nam).

*

Các báo cáo của các linh mục Dòng Tên từ Nước Mặn và Kẻ Chàm được gửi về Tỉnh Dòng Nhật (ở Macao) rồi gửi về Nhà Mẹ của Dòng ở Rome. Báo cáo năm 1621, do João Roiz  viết bằng tiếng Bồ Đào Nha, có các mục “Residencia de Faifo na Provincia de Cacham: Cư sở Hội An ở tỉnh Kẻ Chàm” hay “Residencia de Nuocman na provinia de Pulo Cambi: Cư sở Nước Mặn ở Quy Nhơn” đã nhắc đến các địa danh tiếng Việt: Sinoa (Thuận Hóa), Cacham (Kẻ Chàm/Dinh Thanh Chiêm/Dinh Chàm), Nuocman (Nước Mặn), Ungue (Ông Nghè), Unsai (ông Sãi), Bafu (Bà Phủ).

Cũng năm này, linh mục Gaspar Luis cũng viết báo cáo tương tự về Đàng Trong, rồi cũng gửi về Nhà Mẹ ở Rome, chỉ có một điều khác là báo cáo này viết bằng tiếng Latin, một số từ tiếng Việt trong đó có khác một chút về chính tả.

*

Có thể Pina là người giỏi tiếng Việt nhất. Nhưng hẳn là sự hỗ trợ của các linh mục gốc Nhật đã giúp ông rất nhiều trong việc học tiếng Việt, làm quen với chữ Hán, chữ Nôm. Cũng nhờ vào kinh nghiệm chế tác chữ viết để phục vụ truyền giáo bằng tiếng bản xứ ở khắp thế giới, nhất là ở Nhật, các linh mục Dòng Tên ở Kẻ Chàm và Nước Mặn, tìm ra cách sử dụng chữ cái Latin để ký âm tiếng Việt chuẩn xác nhất có thể. Cho đến nay, tuy có rất nhiều thay đổi, nhưng vẫn có thể đoán được rằng chữ quốc ngữ về gốc gác đã được thiết kế khoa học và tinh xảo.

Việc này đòi hỏi người chế tác phải có trình độ khoa học thuộc hàng cao thủ. Rất có thể có một người tham gia khá nhiều vào việc này, đó là Cristoforo Borri. Ông này sinh ở Milan năm 1583, vào Dòng Tên năm 1601, rồi đến Hội An năm 1618. Borri rất giỏi toán, thiên văn và hàng hải. Ông viết nhiều sách về Hàng Hải, Thiên Văn bằng tiếng Bồ Đào Nna và tiếng Latin. Cuộc sống linh đạo của ông khá rắc rối. Sau khi bỏ Đàng Trong về Bồ Đào Nha, ông dạy toán ở Đại học Coimbra (một đại học rất lâu đời, thành lập từ năm 1290). Ở đó ông nổi danh đến mức được vua Tây Ban Nha mời qua làm việc ở Madrid. Ông bỏ Dòng Tên, theo một hai dòng khác, nhưng đều không ở được lâu.

Cuốn sách của Borri về Đàng Trong được xuất bản lần đầu năm 1621 bằng tiếng Ý. Sau đó được dịch ra tiếng Pháp, tiếng Latin, tiếng Hà Lan, tiếng Đức và tiếng Anh. Trong đó xuất hiện nhiều từ và câu tiếng Việt đơn sơ:  Tunchim (Tonkin, Đông Kinh, Bắc Kỳ), Kemoi (Kẻ Mọi, Tây nguyên ngày nay), Quamguya (Quảng Nghĩa), Dàdèn Lùt (Đã đến lụt, lụt đã đến), scin mocaij (xin một cái), Da an het (đã ăn hết), Tuijciam biet (tui chẳng biết); hoặc có những câu như “Muon bau dau christiam chiam: Muốn vào đạo Christian chăng”.

*

Sau chừng chục năm ở Đàng Trong, các linh mục phương tây bắt đầu quen thuộc với các thanh sắc trong tiếng Việt. Trong thư từ gửi về Rome, họ đã bắt đầu viết tiếng Việt có bỏ dấu. Quãng năm 1624, Pina lúc này đã thành cha bề trên ở cư sở Kẻ Chàm. Ông là người dạy tiếng Việt cho các linh mục Dòng Tên đến sau, trong đó có Antonio de Fontes người Bồ Đào Nha, và Alexandre de Rhodes người Pháp.

Năm 1626, de Fontes viết thư bằng tiếng Bồ Đào Nha, gửi về Rome. Trong đó bắt đầu có những từ tiếng Việt có dấu: Bến Đá, Ondedóc (Ông đề đốc ), Nhít la Khấu (Nhất là không),

Cũng năm này, Buzomi gửi thư viết bằng tiếng Ý về Rome. Trong đó có chữ “thien chũ”, tức là Thiên Chủ (nay gọi là Thiên Chúa). Buzomi là người phát hiện ra nếu dịch Đức Kitô là Thượng Đế sẽ bị lẫn với tôn giáo bản địa lúc đó, đang bị ảnh hưởng của người Hoa, người dân sẽ hiểu Thượng Đế (ông viết là “xán tí”, theo âm tiếng Hoa là “thượng đế:) đồng nhất với Ngọc Hoàng (ông viết là “ngaoc huan”). Ông cũng đề cập đến chùa Ngọc Hoàng ở Đàng Trong (có lẽ chính là chùa mà Obama đã đến thăm): “pagoda por nome, ngaoc huan”.

*

Mười năm sau, năm 1636, Alexandre de Rhodes (tên Việt là Đắc Lộ) đã tương đối khá tiếng Việt, ông viết một cuốn sách bằng tiếng Latin, rồi sau đó tự mình dịch ra tiếng Pháp. Trong cuốn sách này xuất hiện các từ tiếng Việt được viết y như bây giờ: Annam, Chúacanh (Chúa Canh, chúa Cao Bằng, tức nhà Mạc), Chúa Bàng (Chúa Bằng, tức Bình An Vương Trịnh Tùng), Chúa thanh do (Chúa Thanh Đô, tức Trịnh Tráng), cai xã, cai huyen (cai huyện), cai phu (cai phủ), giô (giỗ)

Cùng quãng này, linh mục Amaral đã ra Đàng Ngoài và tài liệu do ông viết tay đã được bỏ dấu (tài liệu viết tay quan trọng ở chỗ các linh mục bỏ dấu được, trong khi sách các vị viết, đem in ở Rome thì bị mất dấu). Tài liệu viết năm 1636 của Amaral có nhiều từ bỏ dấu gần giống ngày nay: nhà ti, nhà hién (nhà ti, nhà hiến), nhà phũ, nhà huyẹn (nhà phủ, nhà huyện), đàng ngoày (đàng ngoài), tế kì đạo (tên một lễ gì đó), đức vương (tức Trịnh Tráng), Chuá cả (tức Trịnh Tạc), Kẻ Chợ, yêu nhău (yêu nhau), thầi (thầy), chặp (tháng chạp), Đình (đình làng), Nghệ An, Bố Chính, …

*

Hai linh mục Dòng Tên người Bồ Đào Nha là Gaspar Amaral và Antonio Barbosa (sinh 1594) lúc này truyền giáo ở Đàng Ngoài, và chắc chắn là giỏi tiếng Việt và giỏi cách dùng ký tự latin để ký âm tiếng Việt (giỏi hơn Alexandre de Rhodes). Amaral soạn từ điến Việt-Bồ-La (Diccionário Anamita-Português-Latin), còn Barbosa soạn từ điển Bồ-Việt (Diccionário Português- Anamita). Cả hai bản thảo chưa được in và đều thất lạc một cách bí ẩn. Trong cuốn từ điển mang tính lịch sử của mình, xuất bản năm 1651, Alexandre Rhodes có nói ông sử dụng hai cuốn từ điển của Amaral và Barbosa.

Đến đây ta có thể hiểu được phần nào, tại sao cách đánh vần tiếng Việt bằng chữ quốc ngữ lại khá giống tiếng Bồ Đào Nha và (hình như, nếu không nhớ nhầm) một phần của cách đánh vần này có tham khảo cách đánh vần ở vùng Catalonia.

[Ở thế kỷ 15, hai cường quốc hàng hải là Bồ Đào Nha và Tây Ban Nha hai thế lực bành trướng và làm bá chủ thương mại thế giới. Tòa thánh ở Rome cho hai nước này bảo trợ việc truyền giáo luôn cho tiện. Khi xích mích giữa hai cường quốc quá căng thẳng, năm 1493 Giáo hoàng Alexandre VI vạch một đường từ Bắc Cực đến Nam Cực, đi qua quần đảo Acores, phía Tây  đường này là vùng của Tây Ban Nha, phía Đông là Bồ Đào Nha. Vậy nên châu Á thuộc vùng khai phá của Bồ Đào Nha. Vua Bồ Đào Nha đặt một phó vương ở Goa (Ấn Độ) để cai trị phía Đông. Ở Goa vì vậy có một tòa tổng giám mục, dưới tòa này là hai tòa giám mục đặt ở Malacca và Macao. Tòa Malacca phụ trách Đàng Trong, Tòa Macao phụ trách Đàng Ngoài. Việc truyền giáo, bản chất cũng rất cạnh tranh. Các dòng cạnh tranh nhau, các tòa cạnh tranh nhau. Đồng thời có hai thế lực hải quân mới nổi lên là Hà Lan và Anh. Hai nước này, không phải Công giáo La Mã, họ không phải tuân theo mệnh lệnh Tòa thánh ở Rome. họ cứ thế mà chinh phục Châu Á. Rồi quãng 1640, chính vua Bồ Đào Nha lại thất thế trước vua Tây Ban Nha.

Hai cuốn từ điển của Amaral và Barbosa được lưu trữ ở Văn khố Tỉnh dòng, Dòng tên, ở Macao.

Từ 1758, Bồ Đào Nha rồi đến Pháp bắt đầu trục suất Dòng Tên ra khỏi đất của mình. Văn khố ở Macao phải chuyển về Dòng Tên ở Manila (thuộc Tây Ban Nha). Nhưng ở đó cũng không yên, vì đến năm 1767, đến lượt triều đình Tây Ban Nha cũng đàn áp Dòng Tên và tịch thu toàn bộ tài liệu ở đây rồi mang về Madrid năm 1770. Có thể bản thảo của Amaral và Barbosa, nếu không bị thất lạc, thì đang nằm ở Madrid.

Vào giai đoạn Dòng Tên bị Giáo hoàng bắt đóng cửa (1773), Dòng Tên đã để mất cả Đàng Trong lẫn Dàng Ngoài vào các dòng truyền giáo khác.]

*

Alexandre de Rhodes, gốc Do Thái,  sinh ở Pháp năm 1593, nhập Dòng Tên năm 1612, đi Châu Á truyền giáo từ Bồ Đào Nha, qua Goa, rồi đến Macao. Ông muốn đi Nhật Bản, nhưng cuối cùng lại được giao đi Đàng Ngoài. Nhưng trước tiên, ông tới Đàng Trong để học tiếng Việt ở cư sở Kẻ Chàm. May mắn cho ông, khi tới nơi, Kẻ Chàm đã có hai linh mục rất giỏi tiếng Việt là Borri và Pina. Pina trực tiếp dạy tiếng Việt cho de Rhodes. Ông còn học thêm tiếng Việt với một em bé 13 tuổi. Hai người học thông qua tiếng Bồ. Em bé này lớn lên lấy tên là Raphael Rhodes, tham gia truyền giáo ở Lào, rồi quay về Đàng Ngoài, lấy vợ và trở thành một thương gia giàu có  nhờ buôn bán hàng xuất nhập khẩu giữa Thăng Long và Phố Hiến.

Bị trục xuất khỏi Đàng Trong năm 1645, ông quay về Châu Âu, rồi đến Rome. Năm 1651, sau hơn một năm ở Rome, Rhodes xin Dòng Tên chi tiền xuất bản hai cuốn sách quốc ngữ đầu tiên: cuốn “Từ điển Việt Bồ La” và cuốn “Phép giảng tám ngày”.

Khoảng 10 năm sau, năm 1660,  ông qua đời ở Iran.

*

Ở Nhà mẹ Dòng Tên ở Rome người ta còn lưu trữ một số tài liệu liên quan đến giai đoạn Dòng Tên truyền giáo ở Đàng Trong và Dòng Ngoài. Trong đó có những lá thư viết tay, bằng chữ quốc ngữ, không phải do các linh mục nước ngoài viết, mà là các thầy giảng (nay gọi là giáo lý viên) người Việt Nam. Trong đó có một lá thư của thầy Bento Thiện, viết năm 1659. Bức thư này được gọi là “Lịch sử nước Annam”.

Thư bắt đầu:

“Thuở ấy có một Vua là Triệu Vũ Hoàng sang đánh Vua An Dương Vương. An Dương Vương lấy nỏ mà bắn thì giặc liền chết. Mà Vua An Dương Vương sinh ra được một con gái tên là Mi Chu. Vua Triệu Vũ Hoàng thì có con trai tên là Trọng Thỉ.”

Trong thư có kể nhiều chuyện, ví dụ chuyện Táo quân:

“Bếp thì thờ Táo quân, gọi là Vua bếp. Nó lấy chồng trước thì sa vào lửa mà chết, nó lại lấy chồng sau mà lòng con thương nghĩa chồng trước, thì chồng sau đi xem nơi lỗ xưa, thì mình cũng sa xuống mà chết. Chồng sau thấy vợ chết, thì cũng gieo mình xuống mà chết, thì ba người vào một lỗ ấy, thì người ta nói bày đặt rằng: ấy là Vua bếp. thì phải cậy cho làm mọi việc nên.”

*

Sau Alexandre de Rhodes, khoảng hơn 100 năm sau, khoảng năm 177x, Pigneau de Behaine (Bá Đa Lộc) viết từ điển Việt-Latinh (Dictionarium Anamitico-Latinum). Tiếng Việt trong từ điển này không khác nhiều với tiếng Việt chúng ta đang dùng. Rồi thêm gần 100 năm nữa, đến năm 1865, tờ báo in bằng chữ quốc ngữ là Gia Định Báo, ra đời ở Sài Gòn.

Còn về Dòng Tên, vì là một dòng đề cao trí thức nên một số quốc gia như Đức và Nga vẫn cho Dòng Tên tồn tại trên đất mình. Năm 1814 Giáo hoàng cho tái lập dòng. Dòng Tên không quay lại Việt Nam vì cơ sở của họ đã mất hết, những người theo Dòng Tên nếu còn sống thì cũng đã già. Mãi đến 1957 họ mới quay trở lại được miền Nam. Theo một nghĩa nào đó, họ đến Việt Nam, để lại chữ Quốc Ngữ, rồi rút đi trước khi Pháp (nói đúng hơn là liên quân Pháp Tây Ban Nha) xâm lược Nam Kỳ. Rồi họ quay lại, sau khi Pháp đã rút đi.

PS: Nếu ai tinh ý, sẽ thấy trong đoạn kinh Lạy Cha ở phía trên có chữ “Coác”. Có thể đây chính là chữ “Quấc”, mà nay được viết “Quốc”. Cuốn từ điển của Huỳnh Tịnh Paulus Của, tên là “Đại nam quấc âm tự vị”. Khi còn ở Pháp, Nguyễn Ái Quốc viết tên mình là “Ái Quấc”.

[image error]

[image error]

 

 

 

 

 

 

Ai yêu ai ư?

Điều thú vị là cuộc tranh cãi cấp độ phát rồ ở tầm vóc quốc gia vừa rồi lại xảy ra hoàn toàn trên mạng, nơi người ta tranh luận bằng cách bấm bàn phím (cả phím vật lý và phím ảo).

Tức là một cuộc tranh luận hoàn toàn bằng text, hoàn toàn không có chút phát âm nào ra đằng mồm. Một cuộc tranh luận của người Việt trên internet về cách đánh vần, về cách phát âm, một cuộc tranh luận ồn ào đến phát điên trong …sự yên tĩnh gần như tuyệt đối (ngoại trừ âm thanh bàn phím và tiếng chửi thề chuyên vần “ồn” hay vần “uồi” của vài người gõ phím).

Trong cuộc tranh cãi ấy, chẳng mấy người tham gia biết được rằng tiếng ta có bao nhiêu nguyên âm, bao nhiêu phụ âm. Chẳng mấy ai biết rằng câu hỏi, ví dụ,  “ai yêu ai ư” toàn là nguyên âm. (nguyên âm đôi “ai”, nguyên âm ba “yêu”).

Và không biết thì có làm sao. Tất cả chúng ta đều lớn lên được, đều đi làm, đều lấy vợ lấy chồng, đều có internet, đều có smartphone, có laptop, để cãi nhau, về cách đánh vần.

Đánh vần không có gì khó. Tất cả chúng ta đều có thể đánh vần câu sau:

A-nh Th-ức Đ-ang T-uyệt Th-ực!

Học thêm một ngôn ngữ!

Ngày nay có lẽ ai cũng hiểu việc biết thêm một ngôn ngữ khác tiếng mẹ đẻ của mình sẽ có ích lợi thế nào trong cuộc sống.

Ngày xưa các cụ ai biết chữ Hán thì oai hơn những người xung quanh hẳn mấy bậc. Gần đây hơn là những trí thức biết tiếng Pháp, rồi tiếng Anh. Hiện nay, trong công việc và đời sống thường ngày, những ai biết các thứ tiếng, Trung, Nhật, Đức, … đều có chút lợi thế hơn những người không biết.

*

Trong thế giới số hiện nay, nơi mà xu hướng trí tuệ nhân tạo đang manh nha xuất hiện ở mọi nơi, còn nền kinh tế chuyển dần sang 4.0, rất có thể hai ngôn ngữ sau đây sẽ đóng vai trò quan trọng trong cuộc sống thường ngày. Một là ngôn ngữ toán nói chung và ngôn ngữ đại số tuyến tính nói riêng. Hai là ngôn ngữ lập trình cho trí tuệ nhân tạo, ví dụ như ngôn ngữ Python.

Có nghĩa là nếu ai biết hai ngôn ngữ nói trên sẽ có thêm một chút lợi thế trong cuộc sống.

*

Biết hai ngôn ngữ nói trên, không có nghĩa là phải thông thạo chúng. Ta chỉ cần biết chúng ở mức đọc hiểu. Cũng giống như học ngoại ngữ, ví dụ tiếng Anh, nếu giỏi đến mức viết được tiểu luận hay hùng biện bằng tiếng Anh được thì tốt, còn không thì chỉ cần đọc hiểu là được: đọc được báo tiếng Anh, đọc phụ đề phim tiếng Anh, và cũng nhất thiết phải hiểu 100% những gì họ viết.

*

Toán là một thứ ngôn ngữ. Chỉ có điều nó không phải là ngôn ngữ tự nhiên, nó là ngôn ngữ do con người chủ ý tạo ra và được hoàn thiện dần theo thời gian.

Quãng năm 1557, có một nhà toán học xứ Wales tên là Robert Recorde. Ông này phát chán với việc làm toán mà cứ phải viết cái này bằng với cái này, ông nghĩ ra cách thay cụm từ “bằng với” bằng dấu “=”. Từ đó dấu “=” xuất hiện trong các công thức toán.

Hoặc trước đó, vào năm 1525, nhà toán học người Đức Christoph Rudolff thấy cứ phải viết chữ căn (root) của số nào đó mãi cũng chán, ông ấy biến chữ r (ký tự đầu của chữ “root”) thành dấu căn “ √ ”, và từ đó chúng ta có dấu căn trong toán học.

Ông René Descartes còn lười hơn nữa. Không chỉ nghĩ thêm từ vựng cho toán, ông ấy đặt thêm cả ngữ pháp. Khoảng năm 1637, thay vì viết phép nhân nhiều lần cùng số “x”, ví dụ “x.x.x.x” rất dài dòng và mệt, thì ông ấy viết “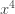”. Descartes cũng là người quy ước dùng các số ở cuối bảng chữ cái “x,y,z” để chỉ các biến số “chưa biết, cần phải tìm”.

Ông Gottfried Leibniz thì nghĩ ra cách viết các dấu vi phân “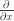”  và dấu tích phân ““. Euler thì nghĩ ra các ký hiệu nay rất quen thuộc: “e,  i, f(x), ”.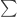

*

Nếu ta biết tiếng Anh căn bản, ta có thể tra từ điển để đọc một tờ hướng dẫn sử dụng thiết bị được viết bằng tiếng Anh. Cũng vậy, nếu biết một chút từ vựng và ngữ pháp của toán, ta sẽ biết cách tra “từ điển” để tìm nghĩa của từ và ngữ pháp trong các công thức toán học mà ta phải tự đọc hoặc tự tìm hiểu cho công việc của mình, hoặc để mở mang kiến thức.

Ví dụ 1. Trong cơ học lượng tử, các nhà vật lý luôn quan tâm đến việc xác định vị trí và vận tốc (hay động lượng) của một hạt (ví dụ electron) trong không gian. Vị trí của hạt ở một thời điểm bất kỳ được xác định bằng các tọa độ x,y và z.

Theo kiến thức vật lý phổ thông, chúng ta ai cũng biết công thức (trong đó “p” là động lượng của hạt, bằng khối lượng của hạt là “m” nhân vận tốc của hạt là “”). Giờ giả sử chúng ta biết thêm một phép toán (toán tử) nữa, có tên gọi là toán tử giao hoán, được ký hiệu bằng dấu [x,y].

Nếu toán tử giao hoán này bằng không,  , nghĩa là hai đại lượng “x” và “y” có khả năng giao hoán. Ý nghĩa vật lý của nó là ta có thể đồng thời xác định được cả “x” và “y” (tức là ta có thể đồng thời đo được chính xác tọa độ trục x và tọa độ trục y của hạt).

Nếu toán tử giao hoán này khác không, , nghĩa là x và p không có khả năng giao hoán. Ý nghĩa vật lý của nó là nếu ta biết (đo được) chính xác vị trí “x”, thì không thể đo được chính xác giá trị của động lượng “p”.

Nếu viết chính xác hơn, ta có . Đây chính là Nguyên lý bất định Heisenberg. Nguyên lý này phát biểu bằng lời như sau:  “Ta không thể đồng thời xác định chính xác được cả vị trí lẫn vận tốc (xung lượng) của một hạt. Nếu ta biết càng chính xác đại lượng này, thì ta biết kém chính xác đại lượng kia”. Nếu phát biểu bằng  toán học, nguyên lý này được viết ngắn gọn như sau:

 

*

Ví dụ 2. Giả sử ta quên hết kiến thức toán, và cũng không hiểu gì về hàm sóng trong cơ lượng tử; nhưng ta vẫn nhớ một quy tắc cơ bản của ngữ pháp trong ngôn ngữ toán học: cần chặt chẽ và logic trong suy luận. Giờ chúng ta cùng nhìn vào phương trình sóng của Schrödinger:

Được cho biết (toán tử năng lượng Hamilton) là số thực,  (hằng số Planck rút gọn) là số thực, i là số ảo (), ta có thể suy luận như sau: nếu   mà là số thực, thì hai vế của phương trình sẽ mâu thuẫn nhau, vế phải là số thực, vế trái là số phức (do có chứa thành phần là số ảo i). Để không mâu thuẫn, hàm sóng   buộc phải là số phức. Nhưng hàm sóng mà là số phức (có thành phần là số ảo i), thì không thể đo lường bằng thực nghiệm (mọi đại lượng muốn đo lường được thì phải là số thực).

Chính tác giả của phương trình sóng nói trên, nhà vật lý Schrödinger, cũng bí và không biết giải thích hàm sóng này là gì. Sau đó nhà vật lý Max Born mới đề xuất một ý tưởng, ông lấy bình phương hàm sóng, , và sau khi bình phương nó  trở thành số thực, và tỷ lệ với xác suất tìm thấy một hạt ở một điểm cho trước trong không gian (xác suất là một đại lượng ta có thể đo được). Đề xuất này đã mang đến cho Max Born một giải Nobel Vật lý.

*

Trong Ví dụ 2 ta thấy một khái niệm rất khó hiểu trong vật lý lượng tử, rất khó diễn đạt bằng lời, nhưng khi diễn đạt bằng ngôn ngữ toán học lại dễ hiểu, ngắn gọn và chính xác. Ngay cả khi ta quên gần hết kiến thức toán, chỉ nhìn vào công thức và được giải thích thêm một chút là ta hiểu.

Nói rộng ra, nếu ta biết từ vựng và quy tắc ngữ pháp của toán, ta sẽ dễ dàng đọc hiểu những gì người khác diễn đạt bằng ngôn ngữ toán:

Ví dụ 3: Nhìn vào phương trình (x – a)2 + (y – b)2 = R2 ta sẽ hiểu ngay đây phương trình biểu diễn một đường tròn trên mặt phẳng, trong hệ tọa độ hai trục x và y. Đường tròn này có bán kính R và  tâm là điểm có tọa độ trên trục x là “a” và trục y là “b”.

Ví dụ 4: Đây là phương trình Fisher: . Trong đó i là lãi suất danh nghĩa, r là lãi suất thực, là lạm phát kỳ vọng. Để đơn giản hóa, người ta tính xấp xỉ phương trình này: . Tức là nếu ta muốn biết lãi suất thực mà ngân hàng trả cho các khoản tiền gửi tiết kiệm, ta chỉ cần lấy lãi suất danh nghĩa (tức lãi suất ngân hàng công bố) trừ đi lạm phát.

*

Ngôn ngữ toán học cũng chính là ngôn ngữ mà trí tuệ nhân tạo (AI) giao tiếp với thế giới bên ngoài để  tự học hỏi và dần trở nên hiểu biết và thông minh hơn. Nó dùng ngôn ngữ toán để tiếp thu thông tin từ thế giới xung quanh (thông qua các cảm biến và camera) và từ dữ liệu trên internet.

Tên gọi “trí tuệ nhân tạo” tự nó đã có nghĩa là một loại “trí tuệ” do con người tạo ra. Con người tạo ra trí tuệ ấy bằng cách lập trình. Để lập trình được, họ dùng “ngôn ngữ lập trình”, là một ngôn ngữ cũng do con người tạo ra để nói chuyện với máy móc. Ngôn ngữ lập trình cũng có sự tiến hóa riêng của nó, và càng ngày nó càng giống ngôn ngữ tự nhiên của chúng ta, cụ thể là nó rất giống tiếng Anh giao tiếp.

Ví dụ 5. Giả sử ta muốn bảo “máy” tính tổng của hai số bất kỳ (do ta tùy ý nhập vào máy). Phần Source Code thể hiện các dòng lệnh “input” cho phép ta nhập số liệu và hiển thị câu chỉ dẫn để nhập liệu “Enter first number”. Phần Output thể hiện chương trình khi được “run” (có nghĩa là “chạy” chương trình). Trong ví dụ này, người chạy chương trình nhập số thứ nhất (number 1) là 1.5 và số thứ hai (number 2) là 6.3. Kết quả cho biết tổng (sum) là 7.8.

Nếu đọc từng dòng lệnh, ta thấy ngôn ngữ lập trình dùng để điều khiển máy tính không khác gì ngôn ngữ (ở đây là tiếng Anh) được sử dụng hằng ngày.

[image error]

Ví dụ 6: Giả sử ta muốn lập một chương trình mà ta có thể nhập vào ba con số rồi bắt chương trình ấy tìm ra số lớn nhất. Đọc kỹ từng dòng lệnh, ta sẽ thấy phần so sánh các con số sử dụng ngôn ngữ rất gần gũi với con người: nếu (if) và (and) thì (elif), còn nếu không thì (else). Phần kết quả (ouput) cho ta biết số lớn nhất trong ba con số được nhập vào.

[image error]

(Hai ví dụ về lập trình ở trên là ví dụ của trang dạy lập trình Programiz, cả hai ví dụ này đều sử dụng ngôn ngữ lập trình Python.)

*

Học để thành thạo và giỏi hai ngôn ngữ “toán học” và “lập trình” chắc là rất khó. Nhưng học để biết hai ngôn ngữ này, để sẵn sàng đón nhận kỷ nguyên của AI và IoT (Vạn vật trên Internet – Internet of things), thì không quá khó. Chỉ cần bỏ thời gian và chăm chỉ học. Ngôn ngữ lập trình ngày càng gần gũi với tiếng Anh giao tiếp; còn đại số tuyến tính, là loại toán được sử dụng nhiều trong AI, thực ra cũng chỉ khó vừa vừa, bởi nó chỉ xoay quanh (và đi xa hơn một chút) các phép toán cộng, trừ, nhân, chia thông thường.

Nói cách khác, hai ngôn ngữ này có thể sẽ có vai trò quan trọng trong tương lai gần. Ai cũng nên học, nhất là những người trẻ tuổi, bởi họ sẽ phải sống phần lớn cuộc đời mình trong thế giới của AI. Rất có thể trong tương lai, mọi người thay vì nói chuyện với nhau bằng tiếng Việt, Trung, Pháp Anh … họ sẽ nói với nhau bằng ngôn ngữ lập trình. Thậm chí họ có thể còn phải nói với “máy móc”.

Có thể một ngày nào đó họ sẽ quen thuộc với việc ra lệnh bằng ngôn ngữ lập trình. Buổi sáng thức dậy, họ bảo cái máy hút bụi có gắn chip AI và kết nối internet trong nhà mình: “Mày ra ngoài phố mua cho tao tờ báo giấy!”

*

Hai nhà vật lý hàng đầu thế kỷ 20 là Einstein và Dirac cũng đóng góp rất nhiều vào từ vựng và ngữ pháp của toán. Vì lười nên Einstein gét cách viết tổng . Ông viết ngắn gọn: , trong đó i không phải là lũy thừa bậc i, mà là chỉ số trên hoặc dưới, cứ có 2 chỉ số thế này, nghĩa là phép tổng với i chạy từ 1 đến 3. Trong phương trình trường của Thuyết tương đối, i chạy từ 0 đến 4.

Tích Cik của ma trận Aij  (i hàng, j cột) với ma trận cột Bjk (j hàng, k cột) nhìn phức tạp thế này:

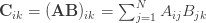
nhưng nếu dùng cách viết tổng của Einstein sẽ chỉ còn ngắn gọn thế này:

Dirac thì nghĩ ra ký hiệu Bra-Ket. Vector Ket, , là vector trạng thái, thực chất là ma trận cột. Vector Bra, , bản chất là số phức liên hợp của Ket, và là ma trận hàng.

Nhờ các cách viết của Einstein và Dirac mà các phép tính nhân ma trận (và cũng là nhân vector) trở nên gọn gàng đơn giản. Phương trình Einstein (thuyết tương đối) và phương trình Schrödinger (hàm sóng) có dạng ngắn gọn như sau:

Phương trình Einstein:

Phương trình Schrödinger:

Mọi người có thể so sánh với cách viết bình thường phương trình Schrödinger cho hạt trong hệ tọa độ 3 chiều:

 

Trong phương trình trên, ta thấy ký hiệu  (napla bình phương). Đây cũng là một “cú pháp” do ông Laplace người Pháp nghĩ ra (chắc cũng vì lười). Bởi vậy nó có tên là toán tử vi phân Laplace. Thay vì viết “tổng các đạo hàm bậc hai theo 3 trục tọa độ x, y, z:  “, ta có thể viết ngắn gọn thế này: “” là xong.

*

Một phần của bài viết trên đã đăng trên TTCT (tuần báo), số ra tuần này. Còn bài viết dưới đây là về sự kiện anh Đàm Thanh Sơn được giải Dirac, bài cũng đã đăng trên TT (nhật báo) số ra ngày hôm nay. Báo TT ngày hôm nay này dành 2 trang đăng các bài viết về anh Sơn, có bài của anh Ái Việt nữa.

GS Đàm Thanh Sơn nhận giải Dirac

Giải thưởng Dirac 2018 (Dirac Medal 2018) mới được trao cho ba nhà vật lý lý thuyết xuất sắc Subir Sachdev (Đại học Harvard), Đàm Thanh Sơn (Đại học Chicago) và Xiao-Gang Wen (Học viện công nghê Massachusetts – MIT)— vì các nghiên cứu độc lập của ba nhà vật lý này đã góp phần mang đến những hiểu biết sâu sắc và mới mẻ cho vật lý lý thuyết. Các nghiên cứu của ba nhà vật lý nhận giải Dirac năm nay đã đưa ra các kỹ thuật mới và độc đáo trong hệ đa –thể (many-body system).

Các nghiên cứu của ba nhà vật lý nói trên liên quan đến các hiệu ứng của cơ học lượng tử tác động lên hệ đa thể quy mô lớn (hệ đa-thể là một nhóm các hạt vi mô).

Trong cuộc sống thường ngày chúng ta quen thuộc với ba dạng (pha) của vật chất là rắn, lỏng, khí. Tuy nhiên trong vật lý lượng tử hiện đại, khi ta thay đổi thật chậm các tham số bên ngoài như nhiệt độ và áp suất, vật chất sẽ “chuyển pha” và do đó đột sinh các đặc tính mới.

Các nhà vật lý từ lâu đã có hiểu biết sâu sắc về việc các định luật của cơ học lượng tử tác động lên một nhóm nhỏ các hạt. Nhưng như chúng ta cũng biết, các đối tượng vật chất thường ngày chứa các nhóm hạt vi mô có số lượng cực kỳ lớn. Số lượng hạt trong nhóm là rất lớn, ngay cả so với trí tưởng tượng thông thường gần tới 1023 (một con số có tới 23 con số 0 đứng sau, nếu ta so với số đếm là tỷ, chỉ có 9 con số 0 đứng sau). Trong một hệ có hằng hà vô số hạt vi mô như vậy, sẽ có vô vàn cách thức để các hạt tương tác với nhau. Hệ quả là để áp dụng cơ học lượng tử lên hệ đa-thể này là cực kỳ phức tạp về mặt toán học.

Chìa khóa để hiểu các đặc tính của hệ đa-thể là phải sử dụng hình thái toán học số phức của liên đới lượng tử (quantum entanglement) để tìm hiểu các đặc tính của vật chất. Các công trình của ba nhà vật lý Đàm Thanh Sơn, Subir Sachdev, Xiao-Gang Wen đã đóng góp những ý tưởng và phương pháp cực kỳ mới mẻ giúp làm sáng tỏ các hình thái của liên đới lượng tử electron có thể tạo ra các đặc tính mới của vật chất như thế nào.

Những hiểu biết mới về tính chất vật lý của hệ đa-thể, nhờ vào công trình của ba nhà vật lý được giải Dirac năm nay, sẽ giúp thế giới khoa học hiểu được các đặc tính khác nhau của vật liệu, từ đó có thể thiết kế các vật liệu mới dùng trong các ứng dụng như các thiết bị siêu dẫn hay tính toán lượng tử.

Giáo sư Đàm Thanh Sơn là cựu học sinh Chuyên toán Đại học tổng hợp Hà Nội. Anh đoạt huy chương vàng toán quốc tế (IMO) với số điểm tuyệt đối 42/42 năm 1984 khi mới 15 tuổi.

Giáo sư Đàm Thanh Sơn là nhà vật lý lý thuyết đầu tiên sử dụng các hiểu biết vật lý của lưỡng tính trường chuẩn/trọng trường (gauge/gravity duality) để nghiên cứu các vấn đề tương tác trong hệ đa-thể, từ pha của nhiệt độ cực thấp là các hạt nguyên tử bị bẫy đông lạnh (cold trapped atom) đến pha của nhiệt độ cực cao là plasma của các hạt quark-gluon.

Giáo sư Đàm Thanh Sơn có những công trình quan trọng giúp thúc đẩy sự phát triển sự hiểu biết của lý thuyết trường chuẩn (gauge theory). Đây là  một lý thuyết rất quan trọng trong vật lý hiện đại. Công trình của Giáo sư Đàm Thanh Sơn liên quan đến Thống kê Fermi-Dirac và Phương trình Dirac (một trong những phương trình được bình chọn là đẹp nhất của vật lý lý thuyết, vì phương trình này tiên đoán được hạt “phản vật chất” và là phương trình đầu tiên kết hợp được lý thuyết cơ học lượng tử là Thuyết tương đối hẹp của Einstein.)

Các lĩnh vực nghiên cứu của Giáo sư Đàm Thanh Sơn bao gồm: Lý thuyết dây, Vật lý hạt nhân, Vật lý vật chất mật độ cao, Vật lý nguyên tử.

Công trình được giải Dirac năm nay của Giáo sư Đàm Thanh Sơn nằm trong lĩnh vực Vật lý nguyên tử.

Giáo sư Đàm Thanh Sơn là viện sĩ Viện Hàn lâm Khoa học tự nhiên và Khoa học Xã hội Hoa Kỳ (American Academy of Arts & Sciences), và viện sĩ Viện Hàn lâm Khoa học quốc gia Hoa Kỳ (National Academy of Sciences ).

Giải thưởng Dirac được trao hằng năm vào ngày 8 tháng 8, là ngày sinh của Dirac.

 

 

Thằng gánh nước Deschamps

Eric Catona khi ở thời đỉnh cao của mình đã gọi Deschamps bằng nickname có tính coi thường: thằng gánh nước của đội tuyển. Ý nói nhiệm vụ của Deschamps là thu hồi bóng rồi trả bóng ra xung quanh cho các đồng đội biết cách xử lý tiếp với trái bóng.

Đội Pháp của Deschamps ở chung kết World Cup năm nay đá cực kỳ giống Juventus thời đỉnh cao.

Đội Juvetus đá thế này. Nó đá nhì nhằng cả trận, nhìn cứ như rập rình ở cửa dưới, sắp sửa dính bàn thua đến nơi. Thế mà không có cách gì ăn được nó. Hóa ra nó vừa đá vừa toan tính rất kỹ. Rồi mỗi khi có cơ hội bé tí, nó chuyển sang tấn công, như một đợt bùng phát mãnh liệt, rất nguy hiểm. Nhưng chỉ được chừng chưa đến một phút là nó lại quay lại đá nhì nhằng, xem rất chán và sốt ruột. Thế nhưng, cả trận tẻ nhạt như thế, đến phút 80 tỷ số là 0-0, đến phút 90 thì Juventus thắng 2-0. Thế mới tài.

Để đá được như thế chất lượng cầu thủ phải rất tốt: vừa vững kỹ thuật, vừa thạo chiến thuật, lại cực kỳ tuân thủ nghiêm túc kỷ luật chiến thuật, không ai có cái tôi cao hơn đội bóng. Đội tuyển quốc gia thường có chất lượng cầu thủ khó mà bằng câu lạc bộ nhà giàu, lý do là đội tuyển quốc gia không thể vung tiền ra mua các ngôi sao mình muốn và phù hợp với lối chơi của đội. Nhưng năm nay đội Pháp thì khác, hơi nhiều sao.

Lưu ý là Pháp của Deschamps ở World Cup lần trước bị loại vì thua Đức, sau đó bạn Đức này vô địch. Còn ở Euro cách đây 2 năm, Pháp của Deschamps vào đến chung kết và thua Bồ.

Croatia cũng không phải tay vừa. Nước bé tí, chưa đến 5 triệu dân. Tách ra thành nước độc lập năm 1991, thế mà năm 1998 đã lần đầu vào chung kết World Cup. Đội lúc đó có 2 ngôi sao. Một là Boban, các fan của AC Milan ở Hà Nội lúc bấy giờ rất đông và đều biết anh này. Hai là Suker, đá cho Real. Cả hai anh này đều có cúp C1. Trong trận gặp Pháp, Suker ghi bàn trước. Pháp gỡ 2 bàn nhờ Thuram, cầu thủ cả đời không ghi bàn cho đội tuyển. Sau trận này thì Pháp vào chung kết và vô địch, còn Croatia tranh 3-4 và đoạt giải 3.

Năm nay Croatia có Modrik, bỏ túi mấy cái C1 với Real. Bên Pháp có Varane số 4, còn trẻ cũng nhiều C1 như Modrik, do cũng đá ở Real.

Nhưng quan trọng nhất, đó là giống Zidane, Deschamps rất có thể có chân mệnh thiên tử. Ở Pháp chỉ có một câu lạc bộ duy nhất dành cúp C1, được nhõn 1 lần, là OM,  thì lúc đó đội hình OM có Deschamps.  Sau đó OM dính bê bối và phải xuống hạng, Deschamps qua đá cho Juventus và làm thêm cái C1 nữa. Ở đội tuyển quốc gia anh này làm đội trưởng đội tuyển Pháp vô địch World Cup, rồi 2 năm sau vô địch Châu ÂU.

Đội Juventus cũng dính scandal và phải xuống hạng (đời anh Deschamps này dính vào 2 câu lạc bộ xuống hạng vì bị phạt), Deschamps quay lại làm huấn luyện viên và đưa Juventus thăng hạng. Nhìn vào cách bố trí hàng tiền vệ tới 5 người của Deschamps ở tuyển Pháp hiện nay, rất dễ dàng nhận ra sự tương đồng với hàng tiền vệ 5 người của huấn luyện viên Conte ở Juventus.

(Anh Conte đá 5 tiền vệ với Pirlo là nhân vật chính, ở dưới là 3 hậu vệ, còn Deschamps vẫn dùng 2 trung vệ + 2 hậu vệ, mà hậu vệ cánh thì chỉ có Pavard là lên tấn công. Trung vệ Umiti toàn đứng dưới mỗi khi đội nhà đá phạt, có mỗi hôm vừa rồi tự nhiên lao lên, thế là đánh đầu ghi được 1 bàn duy nhất, đưa Pháp vào vòng trong, khá giống vụ Thuram. Griezmann và Mbappé tuy trên danh nghĩa là forwarder nhưng đá như tiền vệ. Chỉ có anh Giroud là tiền đạo. Anh Giroud này có một ưu điểm cực kỳ lớn đó là chân gỗ. Vì chân gỗ nên anh ta không có cái tôi, và tinh thần của anh là phục vụ đồng đội. Anh di chuyển rất rộng và làm tường rất tốt.)

Cho đến trước trận chung kết cuối tuần này, Croatia đã tung hết sức (ba trận liền đá hiệp phụ) và có lẽ là cũng đã tung hết bài. Còn Pháp chả có bài gì ngoài bài đá nhì nhằng, và đó là bài chẳng có ai bắt được. Chưa kể trận cuối cùng ở vòng bảng, Pháp đã bỏ đi cái kiểu kiêu hãnh và sĩ diện hão, để chơi một trận bóng tẻ nhạt nhất giải, cốt để giữ sức, giữ chân, giữ tay.

Những cầu thủ ngày xưa gọi là match maker, kiểu như Zidane, ngày càng hiếm dần trong bóng đá hiện đại. Không phải vì chất lượng cầu thủ kém đi, mà vai trò match maker nằm ngoài sân, đó là Conte, là Mourinho, Simeone, Klopp, và cả Zidane nữa khi anh này làm HLV cho Real Madrid. Trận tới đây của Modrik và Rakitic, những người vẫn còn phải làm match maker cho đội tuyển của mình, sẽ không phải là đá với ai trên sân, mà đá với người ngoài sân như thế nào, đấy mới là chuyện xoắn não. Trong sân các cầu thủ Pháp cứ nhì nhằng mà đá, còn việc nặng nhất là gánh nước, đã có Deschamps lo.

Giải World Cup năm nay cũng cho thấy vai trò của quản trị ngày càng lớn. Cuộc đấu giữa các đội tuyển là đấu phong cách và trình độ quản trị với nhau. Do khoảng cách trình độ quản trị của các đội ngày càng thu hẹp và chuẩn hóa, nên tính đa dạng của World Cup mất dần, các đội đá như Châu Âu cả, kể cả đội khá kém là Hàn. Đồng thời thắng thua không còn dễ đoán như trước. Nhiều trận kết thúc với tỷ số chênh lệch 1 bàn là vậy.

Bài viết trên là để câu view cho cuốn sách sau, mọi người có thể đọc cuốn sách này (https://5xublog.wordpress.com/2018/05/01/tai-ban-bau-troi-chieu-an-giau-ebook/) trong lúc chờ đến chung kết.

Tái bản: Bầu trời chiều ẩn giấu (ebook)

Anh ngồi, viết những mẩu giấy nhỏ

Chưa bao giờ em biết

Vì anh chẳng gửi đi 

Lời bài hát “Lại một bài tình ca nữa” của nhóm Gạt Tàn Đầy –

Hát cho những tháng ngày khó khăn, em biết đi tìm thức ăn, cho cả anh 

Em lại gần đây anh hát cho nghe, hát cho những đêm đông khó khăn

Em đến bên ai đắp chăn mà ngủ quên

Lời bài hát “Cho” của nhóm Ngọt –

 

Tôi mới “tái bản”, “có sửa chữa và bổ sung”, cuốn Bầu trời chiều ẩn giấu. Các bạn có thể download (miễn phí): bản để đọc trên thiết bị di động ở đây, và bản để in ra giấy ở đây. Cám ơn Long Trần một lần nữa gia công ebook này.

Để tiện cho những bạn đã đọc phiên bản trước, tôi list ra dưới đây các bổ sung và số trang kèm theo.

Lúc đầu tôi chỉ định sửa chữa các sai sót của cuốn sách. Nhưng rồi lỡ tay viết thêm có hai câu ngắn về năm diệu kỳ của Einstein, nên thành ra phải bổ sung thêm khá nhiều đoạn vào nhiều chỗ khác nhau trong cuốn sách.

Đó là năm 1905, Einstein lúc này mới 26 tuổi, đăng liền tù tì 4 bài báo khoa học. Ba trong 4 bài này đều xứng đáng đoạt khoảng 30 giải Nobel Vật lý (và triết học, nếu có giải Nobel như vậy).

Bài đầu tiên là công trình nghiên cứu của Einstein về hiệu ứng quang điện. Bài này góp phần đặt nền tảng cho vật lý lượng tử, và là công trình mang lại cho Einstein giải Nobel. Bài thứ ba là thuyết tương đối hẹp (đến nay vẫn là thuyết khó hiểu nhất của Einstein). Bài thứ tư là quan hệ vật chất khối lượng với phương trình E=mc2 nổi tiếng. (Xem trang: cuối 13 và đầu 14.)

Từ đoạn bổ sung ngắn ngắn này, đâm ra phải viết thêm vài đoạn nữa. Xin liệt kê dưới đây để bạn những bạn đã đọc edition cũ nhanh chóng dò tìm những đoạn được bổ sung.

+ Đoạn về Minkowski, thầy giáo hồi đại học của Eintstein. Minkowski là người hoàn thiện thuyết tương đối hẹp vào năm 1908 (nay được biết với tên “không gian Minkowski”). Trong đoạn này có nói đến Null Geodesics, một khái niệm quan trọng của spacetime. (Trang 41 và 42.)

+ Một đoạn dài về de Broglie, người sử dụng hiệu ứng quang điện và thuyết tương đối hẹp để phát triển lý thuyết lượng tử của mình, trong đó có công trình đoạt giải Nobel, và một công trình về sau được David Bohm tiếp nối. (Xem trang 20 và 21.)

+ de Broglie liên quan đến thí nghiệm khe hẹp với photon đơn và giao thoa electron, nên vài thông tin về hai thí nghiệm này cũng đã được thêm vào.

+ Do thuyết Broglie-Bohm liên quan đến John Bell, một siêu nhân được các bạn đam mê Phật pháp quan tâm, nên có bổ sung một đoạn ngắn về John Bell và thực nghiệm của Alan Aspect (là lý thuyết và thực nghiệm chứng minh lượng tử là phi định xứ). (Xem trang 21.)

+ Rồi tính phi định xứ sau này lại bị một số nhà vật lý, ví dụ Leonard Susskind, bác bỏ bằng chứng minh toán học, trong lúc các nhà vật lý khác, như Roger Penrose vẫn thấy ok. Các quan điểm khác nhau này đều được thêm vào rải rác trong cuốn sách. (Xem trang 21.)

+ Phần phi định xứ (nonlocality) này cũng được thêm vào phần ER=EPR trong bài về Hawking. Bài này được đưa vào sách thành một chương riêng (Chương 5). Chương này tất nhiên có liên quan đến phần lượng tử của Heisenberg ở Chương 2. (Hơi tiếc là lẽ ra nói đến Heisenberg thì phải thêm một chút về khai triển Fourier, và nói đến Schrödinger thì phải thêm một chút về phương trình Klein-Gordon. Nhưng có lẽ để phiên bản sau.) (Chương 5 này bắt đầu từ trang 40.)

+ Ở Chương 2, tôi có đưa vào một đoạn rất ngắn, giải thích nôm na về phương trình Schrödinger, cả dạng tường minh và dạng trừu tượng (và do đó có nhắc đến ket vector và bra vector của Dirac). (Xem trang 16.)

+ Trước đó tôi có thêm một chút về Max Born và việc ông này mãi mới được giải Nobel (dù ông có công đặt nền tảng cơ lượng tử cùng Heisenberg). (Xem cuối trang 14.)

+ Tôi cũng thêm một đoạn ngắn về phương trình trường Einstein (thuyết tương đối tổng quát) với các giải thích nôm na về ý nghĩa hai vế của phương trình. (Xem trang 25.)

Nhưng hơi tiếc là trong phiên bản này tôi chưa nói được về phương trình Friedmann, và qua đó nói thêm về sự tiếc nuối của các nhà vật lý rằng lẽ ra Newton phải phát hiện được vũ trụ giãn nở, thay vì tĩnh tại, và nếu Newton làm được như thế (thay vì đi đầu tư chứng và mất tiền) thì vật lý nói chung và vũ trũ học nói riêng chả cần đợi đến tận thời của Hubble). (Tuy nhiên có thể xem thêm ở cuối bài này)

+ Tuy vậy, ở phần trước khi nói đến phương trình Einstein, tôi có phải thêm một đoạn ngắn khác viết về tính bất ổn định của nghiệm Friedmann. (Xem trang 12.)

+ Mà đã nói về Friedmann, lại phải thêm một đoạn ngắn về George Lemaitre, vị linh mục dòng Tên kiêm nhà vật lý lý thuyết, người đề xuất, và là cha đẻ của thuyết Big Bang, mà trong đó vũ trụ đang giãn nở. Đoạn này góp phần làm dễ hiểu hơn về ý nghĩa các phát hiện của Hubble, của hằng số vũ trụ lambda, ý nghĩa của “năng lượng tối”. (Xem trang 12.)

+ Bởi vì phần “năng lượng tối” được bổ sung, nên “phần vật chất tối” cũng được thêm một ít.

+ Vì cuốn sách này nói nhiều đến thuyết dây nên lần này hai thuyết khác cạnh tranh với thuyết dây cũng được bổ sung thông tin, đó là quantum gravity và twistor theory. (Xem trang 39.)

+ Mà đã nói đến twistor theory và mô hình vũ trụ luân hồi (cả hai đều của Roger Penrose) nên tôi cũng có một chút bổ sung các ý tưởng kỳ lạ của nhà vật lý lão thành và kỳ lạ này.

+ Cuối cùng phần viết về nền khoa học tự nhiên của thế giới Ả rập, tôi có bổ sung thêm chữ “giải thuật” là từ tên của nhà khoa học Arap, ông ông al-Khwārizmī, cũng như chữ “đại số – algebra” là tên một cuốn sách của ông này, cuốn al-jabr. (Xem trang 8.)

Ở phần Lưỡng Hà tôi cũng thêm phần tại sao trong tiếng Việt thì Sunday lại là Chủ nhật. (Xem trang 10.)

Tôi cũng đã upload phiên bản mới vào đường link trong entry giới thiệu phiên bản trước của cuốn sách này.

Hy vọng Bầu trời chiều ẩn giấu, Edition 2018 vẫn tiếp tục được bạn đọc yêu thích, bằng hoặc hơn phiên bản cũ.

Xu béo

Pháp quyền, pháp trị, pháp gì?

Trên trang Luật Khoa tạp chí có một bài dài tìm hiểu về cách dịch khái nhiệm rule of law và rule by law sang tiếng Việt như thế nào mới là đúng. Tên bài là “Rule of Law, không phải ‘pháp quyền’ cũng chả phải ‘pháp trị’.”

Hóa ra vấn đề dịch thuật ngữ này rất lằng nhằng, nhiều học giả cãi nhau như mổ bò, và ngại nhất là các lý luận của họ đôi chỗ rối như canh hẹ. Chưa hết, bài viết này cho ta biết hóa ra bên Tàu họ cũng gặp các vấn đề tương tự.

Mọi người có thể đọc bài ấy ở đây.

*

Hồi bé tôi có đọc một cuốn sách về các nhà sáng chế. Sách kể chuyện về các nhân vật lừng danh kiểu như Thomas Edison. Những sách kiểu này ngày xưa chủ yếu là dịch hoặc phóng tác từ các sách khoa học phổ thông, sách danh nhân của Pháp, rồi sau này là sách Nga.

Trong sách có nói đến ông Benjamin Franklin. Ông này nghiên cứu hiện tượng sét đánh bằng cách thả các con diều lên trời. Nhờ đó ông ấy sáng chế ra cái cột thu lôi. Đến bây giờ tôi vẫn còn nhớ sách nói rằng cái sáng chế ấy thành công đến mức trở thành thời thượng, các quý ông đỏm dáng ở Paris tay cầm ô, đầu đội mũ chóp, đều gắn một cái que kim loại giống như cột thu lôi. Sách cũng nói ông Franklin còn làm đại sứ Mỹ ở Paris.

*

Trong Tuyên ngôn độc lập 1945, người sáng lập nước Việt Nam Dân Chủ Cộng Hòa (founder hoặc founding father của nhà nước Việt Nam hiện nay, theo cách gọi của một số người), có trích dẫn một câu từ Tuyên ngôn độc lập của Mỹ. Tuyên ngôn nổi tiếng của Mỹ này do Thomas Jefferson viết. (Có thể đọc bài về việc ấy ở đây).

Có một nhóm nhỏ vài người Mỹ lãnh đạo cuộc đấu tranh đưa nước Mỹ từ thuộc địa của Anh trở thành quốc gia độc lập, họ cùng nhau ký vào Tuyên ngôn độc lập, cùng nhau ký vào Hiến pháp Mỹ. Họ được dân Mỹ gọi là những người lập quốc (founder), rồi sau này nâng lên là các cha già lập quốc (founding fathers). Trong số đó có Thomas Jefferson, người thành tổng thống thứ ba của Hoa Kỳ. Còn ông Benjamin Franklin nghĩ ra cột thu lôi làm tổng thống thứ sáu.

*

Tôi có xem giáo sư Leonard Susskind giảng về thuyết tương đối hẹp và thuyết trường cổ điển. Phần thuyết trường điện từ Maxwell kết hợp với thuyết tương đối hẹp, ắt hẳn phải nói đến định lý Gauss (phương trình liên tục). Phương trình ngắn gọn này bao gồm hai đại lượng là mật độ điện tích và mật độ dòng điện. Ký hiệu là ρ (đọc là rho) và j. Susskind nói hai ký hiệu toán học này là do Benjamin Franklin đặt ra.

Quả thật, Benjamin Franklin là người đề xuất ý tưởng về định luật bảo toàn điện tích từ rất sớm (quãng năm 1747) và phải gần 100 năm sau nhà vật lý thuộc loại vĩ đại nhất lịch sử loài người là Michael Fraday mới chứng minh bằng toán học thành công (năm 1843).

Franklin cũng là người đặt ra khái niệm tiện tích âm và điện tích dương, ứng với cách viết có dấu ‘-’ và dấu ‘+’ để thể hiện các điện tích này. Cách viết này đến ngày nay vẫn được sử dụng.

Đến đây lại nhắc lại một chút, Benjamin Franklin là một trong những người lập quốc của Mỹ. Giai đoạn nước Mỹ giành độc lập, và Hiến pháp Mỹ ra đời, tương đương với giai đoạn Chúa Tây Sơn bắt đầu manh nha hình thành và khuếch trương lực lượng. Năm Mỹ độc lập là năm Tây Sơn bắt đầu đánh Gia Định (1776). Cùng quãng năm Hiến Pháp Mỹ thông qua (1787) thì Tây Sơn đánh trận Rạch Gầm Xoài Mút (1785) và đại phá quân Thanh (1789).

*

Sau ngày 2-9-1945, nước Việt Nam mới ra đời. Tên là Việt Nam Dân Chủ Cộng Hòa.

Dân Chủ và Cộng Hòa cũng là hai trụ cột chính trong tư tưởng của Thomas Jefferson, người viết Tuyên ngôn độc lập và tham gia vào soạn Hiến pháp Mỹ.

Dân chủ, một khái niệm có từ khoảng 600 năm trước công nguyên (cách ngày nay 2700 năm), hình thành ở Hy Lạp. Ở đó mọi người dân (đúng hơn: mọi đàn ông có của cải) có quyền cùng nhau tham gia thảo luận và bỏ phiếu thông qua các quyết định lớn của thành bang (thị quốc) nơi mình đang sinh sống. Dân chủ Hy Lạp thậm chí còn được luật hóa. Năm 594 trước công nguyên, Solon đã viết luật (sau mang tên ông), tuyên bố rằng mọi người dân phải tự quyết định các vấn đề của thành bang.

Cộng hòa, một thể chế xuất hiện ở Rome (Lã Mã) sau thời gian Dân chủ xuất hiện ở Hy Lạp một chút. Sau khi ông vua thứ 7 của La Mã là Tarquin Kiêu Ngạo bị ám sát (năm 495 trước công nguyên), dân thành Rome phát chán mấy ông vua. Họ bầu ra các viên quan chấp chính, có nhiệm kỳ một năm, giống như bầu CEO ngày nay, để cai quản thành phố. Lúc đầu chỉ có một ông quan, thường có xuất thân nhà giàu, hoặc quý tộc giàu có. Nhưng dân Rome không hài lòng với một ông tổng quản nhà giàu, họ đấu tranh, mất cả thế kỷ, để hệ thống này bầu lên hai ông quan cùng điều hành đất nước, một ông từ giới thượng lưu, một ông từ giới bình dân. Hai ông quan do dân bầu lên, một ông đại diện cho dân có của cải, một ông đại diện cho dân nghèo, thay mặt nhân dân vận hành đất nước. Vậy là chế độ cộng hòa, lưỡng viện, ra đời. Ngày nay xem thủ tướng Anh đến Hạ Viện cãi nhau, chỗ cãi nhau của Hạ Viện, là đại diện của giới bình dân, vẫn giữ nếp nghèo túng: rất chật chội và nội thất khiêm tốn (tuy vẫn rất đẹp so với tiêu chuẩn học làm sang Việt Nam).

Như vậy dân chủ và cộng hòa có lịch sử là khá lâu đời. Giai đoạn hình thành Dân chủ ở Hy Lạp, và Cộng Hòa ở La Mã, thì ở nước ta đang là thời vua Hùng.

Khoảng 200 năm sau khi Hy Lạp và La Mã có thể chế dân chủ và cộng hòa, thì ở miền bắc Việt Nam bây giờ mới hình thành nhà nước Âu Lạc (quãng năm 258 trước công nguyên)

Người châu Âu và Mỹ có hàng ngàn năm để làm quen, tiếp thu, vận hành và phát triển các thể chế dân chủ, cộng hòa. Còn ở ta thì mới có vỏn vẹn chưa được một thế kỷ. Đã thế còn chưa được thực hành cho ra đầu ra đũa. Câu nói “đời còn dài” hóa ra không phải là câu nói đùa cho có. Vì thế, không phải vô cớ mà dân ta tuy miệng thì đề cao các thể chế nặng về lý tính như cộng hòa, dân chủ, nhưng thâm âm thích thú đến mê muội các thứ cảm tính như nhân trị, đức trị, kỳ vọng mong mỏi một đấng minh quân, một lãnh đạo nhân từ, một quan chức liêm khiết.

Ngay cả những người lý trí hơn, cũng chỉ dừng ở mức “pháp trị”, kiểu “quân pháp bất vị thân”. Nhưng cái pháp trị ấy vẫn chỉ là cái vỏ, vì trong cái ruột người ta vẫn phải dựa vào “nhân trị”, tức là cái ông quan ngồi vận dụng luật để phán xử ấy, phải là một ông quan “thiết diện vô tư” kiểu Bao Công. Mà cái con người (nhân) cai trị đất nước ấy sử dụng công cụ là “luật” để trị con người. “Nhân trị” (tức “đức trị“) hay “pháp trị“, xét cho cùng, chỉ là hai mặt của một thể chế phi cộng hòa, phi dân chủ, và không có quyền con người. Quyền con người sẽ được đề cập  ở phần sau. Và đã nói đến “quyền“, thì hẳn “pháp quyền” là lựa chọn dễ chịu hơn.

Cái “bất vị thân” nói trên đi vào sâu trong tâm khảm nhân dân, là do hàng ngàn năm nước ta chịu chi phối của pháp luật của Trung Hoa. Sau khi thoát khỏi bắc thuộc, đến thời Lý (Lý Thái Tông, 1042) ta mới có luật riêng của mình. Nhưng có lẽ bộ luật đầu tiên này, cũng như các bộ luật cuối cùng (Gia Long, 1815) cũng đều là bắt chước bên Trung Hoa.

Luật của Tàu vào nước ta, có lẽ từ thời Mã Viện (năm 43). Cùng với luật cứng, là luật mềm ngụy trang dưới vỏ Khổng Lão (đạo của hiền nhân quân tử, một kiểu triết học chi phối hành vi cá nhân, kiểm soát xã hội, thay vì chỉ dùng luật cứng, trong đó dân phải thần phục vua, con nghe lời cha, vợ nép dưới bụng chồng, người nay thì phải nghe lời người xưa, nói chung là triệt tiêu phản biện và tiến hóa). Hai cái yếu tố này chi phối xã hội nước ta hàng ngàn năm, có lẽ cho đến tận ngày nay.

*

Trên đây là vài nét về các rào cản lớn nhất cho việc nhập khẩu “rule of law” vào đất nước này, mà ngay cả việc dịch thuật ngữ này cũng đã rất phức tạp. Thế còn việc tuân thủ pháp luật thì sao.

Ở nước ta, vì luật pháp được thực thi nghiêm ngặt ở chủ yếu dưới thời Bắc Thuộc và Pháp thuộc, cho nên trong tâm thức người dân thì việc bất chấp luật pháp có cái gì đó mang tính phản kháng, chống đè nén áp bức, chống cường quyền, bất công.

Cũng như với các khái niệm dân chủ, cộng hòa, người dân phương tây cũng có cả ngàn năm quen sống tuân thủ pháp luật. Bộ luật thành văn đầu tiên được biết đến là Luật Hammurabi. Hammurabi là ông vua Babylon, sống cách nay độ 3700 năm. Để tiện so sánh, lúc đó chúng ta còn chưa đến thời vua Hùng, có lẽ còn đang là các bộ lạc.

Ở thời dân chủ của Hy Lạp, họ cũng có những bộ luật rất khắc nghiệt như luật Draco, ai đọc Harry Potter sẽ nhận ra tên nhân vật này. Thời cộng hòa của La Mã họ khắc luôn bộ luật lên các tấm bia đồng dựng ở những nơi công cộng. Đế chế La Mã rộng lớn được cai trị hoàn hảo bằng luật, trong đó có các sắc thuế. Công dân La Mã tuân thủ luật cực kỳ nghiêm túc.

Ngày nay, khi bạn nghe tổng thống Trump nói “Law and Order”, đó chính là tinh thần của đế chế La Mã.

Khi đế chế La Mã sụp đổ vì quá rộng lớn, vị vua cuối cùng là hoàng đế Đông La Mã, tên là Justinian, đã cố gắng sưu tầm luật La Mã cổ và tập hợp thành Bộ luật Justinian. Đó là quãng năm 527 sau công nguyên. Luật Justinian là tiền thân của các bộ luật hiện đại sau này.

Vào quãng thời gian này ở ta có cuộc khởi nghĩa của Lý Bí (Lý Bôn) chống lại triều đình phương bắc.

*

Đến đây cần phải quay lại với Franklin, nhà lập quốc của nước Mỹ này là người có tư tưởng ủng hộ quyền tự do ngôn luận. Đây là một quyền mà nước Mỹ xếp vào quyền con người (ngôn luận, báo chí, hội họp, tín ngưỡng, tài sản…) mà James Madison, một nhà lập quốc khác của Mỹ, soạn ra thành luật tên là Tuyên ngôn nhân quyền.

Cùng với Dân chủ, Cộng hòa, thì Quyền con người (nhân quyền và xã hội dân sự) là trụ cột thứ ba của nước Mỹ.

Khác với Dân chủ, Cộng hòa, có từ tám đời (hay còn gọi là cái thời cổ hy la), Quyền con người ra đời khá muộn. Nó bắt đầu manh nha xuất hiện cùng với sự hình thành đô thị hiện đại, cụ thể là ở Florence.

Vào quãng năm 1400 thì thành phố này trở nên giàu có, người dân thành phố có tài sản riêng, có sự tự do nhất định mà không còn phải quy phục vào đám vua chúa, quý tộc này nọ. Họ tự do được chọn học cái mình thích, nghiên cứu cái mình quan tâm, và làm nghề mình phù hợp. Khoa học nghệ thuật phát triển. Họ mở màn cho cái mà sau này gọi là thời kỳ Phục Hưng. Ở đó xuất một nhà khoa học và sáng chế lớn là Leonardo Da Vinci, rồi xuất hiện Nicolaus Copernicus và Galilei Galileo. Ở đó cũng xuất hiện một đại gia giàu đến mức khuynh đảo chính trị là gia đình Medici. Rồi nhờ gia đình này mà xuất hiện một nhân vật nữa, ông này tên là Machiavelli, ông viết hai tác phẩm lớn là The  Prince và The Discourses. Hai tác phẩm này sẽ quay lại ở gần cuối bài.

Cùng giai đoạn này, nước ta cực kỳ giàu có phát triển. Đó là thời kỳ nhà Lê, sau chiến tranh chống giặc Minh (năm 1428). Nhà Lê phát triển mạnh về quân sự, kinh tế (sản xuất) và ngoại thương (buôn bán sôi nổi với Châu Âu). Nhưng cũng như thời kỷ đổi mới gần đây, giai đoạn cường thịnh của nhà Lê chủ yếu là kiếm chác làm giàu, khi làm giàu rồi thì bỏ tiền ra mua các giá trị trọc phú thay vì giải phóng con người; thay vì tìm mô hình trị quốc mới thì họ lại quay sang sao chép từ kẻ thù của mình là Trung Hoa. Nên thời kỳ vàng son của nhà Lê không kéo dài được lâu, nó chấm dứt khi nhà Mạc nổi lên tiếm ngôi (năm 1527). Từ đây nảy nòi ra hai ông họ Trịnh và Nguyễn, rồi năm 1558 nhà Nguyễn vào Nam. Xem thêm ở đây.

Tinh thần tự do cá nhân của cư dân thành phố Florence thế kỷ 15 không chỉ thúc đẩy khoa học tự nhiên, khám phá thế giới thiên nhiên, phát triển công nghệ, sáng tạo nghệ thuật, mà nó còn tạo ra một giai cấp mới, những người sống bằng nghề nghiệp, sức lao động của mình, tích lũy tài sản cá nhân cho riêng mình, có lương tâm riêng, tri kiến riêng, tự mình suy xét vấn đề và hành động dựa trên các suy xét cá nhân ấy.

Tinh thần này lan dần vào các phong trào tôn giáo và xã hội sau này. Trong đó có Kháng cách, một nhánh mới của Kito giáo, cổ súy mỗi cá nhân đi theo tiếng gọi lương tâm cá nhân của mình, không phải tuân phục các thể chế tập quyền, tự mình phải bươn chải và chăm chỉ lao động để kiếm sống.

Tinh thần tự do nơi đô thị hiện đại và triết lý mới mẻ của Kháng Cách bắt rễ và sinh sôi nảy nở ở Châu Âu một cách không dễ dàng và không rẻ. Những thay đổi lớn lao này trong nhận thức cá nhân đã dẫn đến các xung đột quyền lợi, chính trị và tôn giáo. Tiếp đó là các cuộc chiến đẫm máu kéo dài hàng chục năm trên khắp Châu Âu. Lòng người toàn là hận thù, cuộc sống thì khổ đau. Từ đó mới nảy ra phong trào Khai Minh (Khai Sáng). Những nhà tư tưởng của Khai Minh rất dũng cảm, mọi phát biểu của họ đều biến họ trở thành lề trái và ngay lập tức có thể bị an ninh tư tưởng tóm cổ. Nhưng họ không hề sợ. Trong những năm 1700, những nhà tư tưởng của phong trào Khai Minh cho rằng theo con người cần sống có lý có lẽ cá nhân, những lý lẽ thông thường trong xã hội mà số đông có thể cùng chấp nhận; trong xã hội đó mỗi cá nhân đều được đối xử bình đẳng, các khác biệt về tôn giáo, quan điểm cá nhân cần được khoan dung, con người cần có nhân phẩm, và nhân phẩm của ai cũng cần phải được tôn trọng và được bảo vệ.

Khoan dung và tôn trọng người khác, tự nhận thức được ai cũng bình đẳng như ai, không phải là chuyện dễ dàng. Cùng giai đoạn Khai Minh ở Châu Âu, ở nước ta là thời kỳ Trịnh Nguyễn phân tranh, các cuộc khởi nghĩa nông dân ở miền bắc, và cuối cùng là khởi nghĩa Tây Sơn ở miền trung. Còn hôm nay là ngày 30-4, đến hôm nay nhiều người nhận ra rằng hòa giải bằng mồm rất dễ, còn khoan dung thực sự, từ tất cả các phía, và tôn trọng nhân phẩm của nhau, nhất là tôn trọng bên thất trận, ở nước ta là một việc khó đến mức gần như hoang đường.

Kháng cách và Khai minh dẫn đến một phong trào xã hội có tên rất hấp dẫn trong tiếng Việt là phong trào Lãng mạn, hình thành sau Cách mạng tư sản Pháp. Lãng mạn không giới hạn trong nghệ thuật mà nó đi vào chính trị và thực hành chính trị ở Paris: Chủ nghĩa lãng mạn đã kết liễu nền quân chủ ở Pháp bằng cuộc cách mạng 1830; cũng là lúc nó đúc kết và cổ súy thành công một trụ cột mới của xã hội (bên cạnh dân chủ và cộng hòa): tự do cá nhân và quyền con người (nhân quyền).

Vào quãng 18xx này nước ta đang ở dưới thời Minh Mạng. Và khoảng 30 năm sau thì Pháp chiếm Nam Kỳ. Thật cũng có lý khi Nguyễn Gia Kiểng có nói một câu đại khái: người Pháp còng tay dân tộc Việt Nam và dẫn vào thế giới văn minh.

Tất nhiên cách làm đó đã thất bại. Lẽ ra người Pháp cần hiểu dân chúng ta vừa lười học vừa lười lao động, thích ăn may, mê đỏ đen, thiếu lý lẽ, thừa cảm tính, ít sáng tạo, nghèo ý tưởng, vậy mà lại thích cãi cọ và hiếu thắng, tính cách thường thì dát chết nhưng động đến quyền lợi cá nhân bé tí thì hung hăng đến kinh người.

Phong trào Lãng mạn Pháp, thông qua còng tay, cuối cùng cũng đến được với các sinh viên thành thị đầu thế kỷ 20. Họ viết văn, làm báo, họ đấu tranh. Nhờ đó chúng ta có nền báo chí tự do cho đến trước 1954 và di sản của nó tồn tại đến 1976. Nhờ đó chúng ta có những câu chuyện thú vị, như nhà thơ lãng mạn Huy Cận đi bắt vua Bảo Đại xuống ngôi. Hay nữ cách mạng lãng mạn Minh Khai thoát ly gia đình đi yêu giai đẹp, toàn anh thuộc loại hải đăng (soái ca) hội kín. Những những cuộc phiêu lưu, cả chính trị và tính ái này đưa nàng ra pháp trường. Và sản phẩm phái sinh từ những mối tình ấy là bậc thang danh vọng của một vị danh tướng.

*

Mới đây Nguyễn Anh Tuấn, viết một bài về Củi và Lửa. Có thể đọc trên Danluan ở link này.

Dân chủ và Cộng hòa không được thực hành liên tục ở Châu Âu, mà bị gián đoạn khá dài. Đến thời kỳ phục hung của thành Florence, các giá trị Hy Lạp và La Mã cổ đại mới được vun trồng trở lại. Để tiến thân, Machiavelli viết một cuốn sách tên là The Prince. Cuốn sách này nói về các kỹ năng và mưu lược để chiếm, giữ và củng cố quyền lực chính trị.

Nhưng như Bertrand Russell nói, The Prince mới chỉ là một phần của học thuyết chính trị của Machiavelli, để hiểu trọn vẹn học thuyết của ông, cần phải đọc nốt cuốn The Discourses.

Trong The Discourses, Machiavelli đã mang trở về phương thức kiểm soát quyền lực kinh điển: nhà nước cộng hòa có ‘check and balance’. Ông cho rằng quyền lực chính danh là quyền lực đoạt được bằng các kỹ năng chính trị, trong một cuộc cạnh tranh công bằng. Các chính phủ được người dân kiểm soát thông qua bầu cử hành pháp và tư pháp sẽ ít độc ác, ít vô đạo đức, ít tiền hậu bất nhất hơn chính phủ độc tài. Ông viết hẳn một chương về các nguyên tắc ‘check and balance’ cần được hiến định: tam quyền phân lập, ba quyền lực kiểm soát nhau sao cho cân bằng. Các viện dẫn minh họa của ông chính là luật Solon (mà ông cho là quá dân chủ, thiếu hiệu quả), chế độ cộng hòa La Mã với các nguyên lão (chính là Senate, thượng nghị sĩ ngày nay) rất tốt, vì các nghị sĩ sẽ luôn mâu thuẫn với nhau, và mô hình tốt nhất là hiến pháp Sparta của Lycurgus. Sparta, ai ở Việt Nam cũng biết, với trận đánh Thermopylae và bộ phim 300.

Quay lại với bài Củi Lửa của Nguyễn Anh Tuấn, có vẻ như ở VN cho đến nay, cái quan trọng và được quan tâm hơn cả là cách giành và vun đắp quyền lực. Còn kiểm tra và và cân bằng quyền lực là cái rất ít được quan tâm, ngay cả từ trong gốc rễ là hiến pháp.

Vậy nên cho đến nay, kể từ ngày Ngô Đình Nhu giới thiệu The Prince (Quân Vương) vào giới tinh anh của Việt Nam (xem link này), cuốn sách này đã có tới 3 hoặc 4 phiên bản, mà gần đây nhất là bản của Nhã Nam và Đông A (bản của Đông A cực đẹp). Còn The Discourses thì tiếc thay, chưa có bản dịch nào, kể cả dịch chơi trên mạng.

*

Ngành vật lý thiên văn có gốc rễ từ thời Ai Cập và Lưỡng Hà cổ đại, tức là khoảng hơn 2000 năm trước. Thế nhưng nó mới chỉ có những bước tiến triển đột biến khoảng hơn nửa thế kỷ gần đây, sau khi Einstein giới thiệu thuyết tương đối rộng, sau khi Hubble tìm ra vũ trụ đang giãn nở (khoảng 1930), và khi chụp được ảnh bức xạ viba nền của vũ trụ (1964). Thế nhưng, ngày nay khi ngồi nhìn lại những gì đã trải qua, các nhà khoa học giật mình vì ngay từ thời Newton, với kiến thức và trí óc của Newton, ông ấy thừa sức tìm ra phương trình vũ trụ (phương trình do Friedmann tìm ra năm 1922), trong đó vũ trụ không tĩnh mà giãn nở. Thậm chí Newton có thể tìm ra được một hằng số Hubble ở pha vật chất nắm vai trò chủ đạo không gian (khoảng 168x).

Tôi xem giáo sư Leonard Susskind giảng môn Cosmology, đến phần phương trình Friedmann, ông bảo không biết sao Newton lại không khám phá ra điều này, có lẽ là do ông ấy bỏ quá nhiều thời gian vào việc đầu tư vốn kiếm lời, và nghiên cứu giả kim thuật để làm vàng.

Rất có thể vài trăm năm nữa, có những nhà nghiên cứu nhìn lại Việt Nam ngày nay và hỏi, sao lúc đó Việt Nam không thế này thế kia, để trưởng thành nhanh hơn, tiến bộ nhanh hơn, văn minh hơn. Câu trả lời có lẽ là vì giới tinh anh của Việt nam lúc đó cũng mải kiếm chác, đầu tư có lãi thật nhanh, hay đắm mình vào các thuật giả kim thời internet.

Cờ người (tiếp theo)

Mọi người đọc bài này của Lê Hồng Hiệp: http://nghiencuuquocte.org/2018/04/26....

Rồi đợi xem thế nào!

Rất có khả năng một con mã sắp qua sông cùng lúc một con xe nhập thành!

Vở kịch “Gió một chiều” khả năng cao có thêm chiều mới.

 

 

 

Kakistocracy

Hôm qua cần phải tra từ nguyên của từ “catacomb”. Đang tra online thì thấy từ điển nó báo ở phần trending tìm hiểu từ nguyên, đứng ở vị trí số một là từ  “Kakistocracy”.

Lúc sau xem twitter của Washington Post, nó tweet là “Từ kakistocracy, có tuổi đời 374 năm, có nghĩa là “goverment by the worst”, vừa nhoi lên trong từ điển”.

Giật mình, tưởng Washinton Post nói đến vụ đánh thuế “trú thân” ở nước mình.

Ngày xưa vua đánh thuế thân

Ngày nay kakis đánh chỗ trú thân dân mình

 

Bức xạ của Hawking

Bài viết cho Tuổi Trẻ Cuối Tuần, để vĩnh biệt Hawking. Đọc trên bản in dễ chịu và dễ hiểu hơn vì layout diễn đạt được các phần khác nhau. Các bạn nên mua …báo in.

*

Phát kiến “Lỗ đen không đen hoàn toàn” và nhiều hiểu biết vật lý sâu sắc khác của Stephen Hawking đã tạo ra các đột phá trong vật lý vũ trụ.

*

**

Stephen Hawking bắt đầu học vật lý ở đại học Oxford khi mới 17 tuổi, trẻ hơn hầu hết các sinh viên cùng khóa. Nhờ trí óc vượt trội, tính trung bình anh chỉ học khoảng một giờ một ngày trong suốt thời gian học đại học. Vào năm cuối cùng ở đại học, anh có triệu chứng của một người già vụng về, hay bị ngã khi đi cầu thang. Đi khám bệnh, bác sĩ chẩn đoán là do uống bia, yêu cầu anh phải ngừng nhậu nhẹt.

Năm 21 tuổi, sau khi tốt nghiệp hạng ưu và chuyển qua làm nghiên cứu sinh, các bác sĩ chẩn đoán Hawking mắc chứng bệnh nan y: xơ cứng teo cơ. Họ dự đoán anh chỉ còn hai năm để sống.

Người thanh niên trẻ trung, có khiếu hài hước và đặc biệt thông minh ấy bắt đầu sống từng ngày của hai năm cuối cùng của cuộc đời trong sự lạnh lẽo tối tăm không hạnh phúc, không niềm vui của chứng trầm cảm. Tình cờ anh gặp Jane Wilde trong một tiệc năm mới. Họ yêu nhau. Tình yêu của Jane kéo Stephen lên khỏi vực sâu trầm cảm và đặt anh trở lại công việc nghiên cứu khoa học.

Thế rồi họ lấy nhau, họ cần tiền để sống, và sự nghiệp khoa học của Stephen Hawking bắt đầu rẽ sang hướng khác.

*

**

Ngành vũ trụ học hiện đại ra đời sau khi Einstein công bố thuyết tương đối tổng quát năm 1915. Đến cuối những năm 1950, ngành này vẫn còn chập chững, và hiểu biết của các nhà vật lý, cả lý thuyết lẫn thực nghiệm vẫn còn khá giới hạn. Qua thập niên 1960, các nhà vật lý bắt đầu có những bước tiến mới nhưng họ chưa đạt được đồng thuận về nhiều vấn đề.

Mặc dù nghiệm Big Bang của phương trình thuyết tương đối Einstein đã được nhà vật lý xô viết Alexander Friedmann tìm ra trong quãng thời gian 1922-1924 nhưng nhiều nhà vật lý, nhất là các nhà vật lý xô viết, vẫn tìm cách từ chối hoặc né tránh thuyết Big Bang, tức là không công nhận vũ trụ và thời gian có điểm khởi đầu (quan niệm vật lý truyền thống cho rằng thời gian không có khởi đầu và không có kết thúc, vô thủy vô chung).

Tương tự như vậy, nghiệm lỗ đen được nhà thiên văn học người Đức Karl Schwarzschild tìm ra năm 1916 bằng cách giải hệ phương trình của Einstein, và cũng có khá nhiều nhà vật lý công bố các công trình nghiên cứu về lỗ đen từ trước khi chiến tranh thế giới thứ hai nổ ra, nhưng rất nhiều nhà vật lý châu Âu cho đến tận đầu những năm 1970 vẫn không tin vào sự tồn tại của lỗ đen.

Nghiệm lỗ đen của Karl Schwarzschild

Năm 1916 , Karl Schwarzschild đã giải hệ phương trình của Einstein và tìm ra một nghiệm kỳ lạ. Theo nghiệm này, xung các ngôi sao có khối lượng cực lớn có một không quyển kỳ ảo (magical sphere). Tất cả mọi thứ, kể cả ánh sáng, khi đi vào không quyển này sẽ bị hút vào ngôi sao khổng lồ và không có cách nào thoát ra được. Schwarzschild còn tính toán được bán kính của không quyển kỳ ảo này. Không quyển ma quái mà Schwarzschild tìm ra, ngày nay được gọi là “event horizon: chân trời sự kiện” hàm ý đấy là nơi xa nhất mà  tầm mắt của người quan sát có thể với tới (sau chân trời là lỗ đen, nơi mà ánh sáng nếu vươn tới sẽ bị nuốt vào và không bao giờ trở ra được).

[image error]

*

Hình vẽ mô tả nghiên cứu về lỗ đen của nhà vật lý trẻ người Mỹ Robert Oppenheimer năm 1939. Do thế chiến thứ hai nổ ra, Oppenheimer đi làm bom nguyên tử, công trình này đi vào quên lãng cho đến thập niên 1960 mới được lục ra.

[image error]

Hình vẽ này sử dụng giản đồ không gian Minkowski để mô tả không – thời gian, trong đó trục thẳng đứng là trục thời gian, trục ngang là không gian.

Khi ngôi sao sụp đổ vào bên trong, trường hấp dẫn ở bề mặt ngôi sao ngày càng mạnh, các nón ánh sáng bị bẻ cong vào trong, và các tia sáng khó thoát ra khỏi ngôi sao hơn. Đến một thời điểm cụ thể, ánh sáng không còn thoát ra được nữa. Lúc này hình thành một vùng không-thời gian mà tất cả những gì trong đó, kể cả ánh sáng, không thể thoát ra ngoài và đến được với người quan sát. Vùng không – thời gian này được gọi là lỗ đen, đường biên của vùng này được gọi là chân trời sự kiện.

 

Trong cuốn Lược sử thời gian, bản cập nhật sau 10 năm phát hành, Hawking đã kể lại giai đoạn đặc biệt này. Nó đặc biệt ở chỗ cuộc sống cá nhân của Hawking thay đổi, sự nghiệp khoa học thay đổi, và qua đó làm thay đổi toàn bộ ngành vật lý vũ trụ hiện đại.

*

**

Năm 1965, một nhà vật lý người Anh tên là Roger Penrose chứng minh được rằng khi một ngôi sao có khối lượng khổng lồ bị đổ sụp vào trong do lực hấp dẫn của chính nó, toàn bộ vật chất của ngôi sao sẽ bị nhốt trong một vùng mà kích thước bề mặt của vùng này sẽ bị co về bằng không. Vì bề mặt có kích thước bằng không nên thể tích cũng bằng không.Toàn bộ vật chất của ngôi sao bị nén vào một thể tích bằng không, thì mật độ vật chất và độ cong của không-thời gian trở nên vô hạn và vô cực. Đây chính là cái được các nhà vật lý gọi là một điểm kỳ dị (singularity). Điểm kỳ dị này được chứa ở bên trong một vùng không gian kỳ ảo mà ngày nay quen thuộc với tên gọi lỗ đen. Tên gọi lỗ đen (black hole) do nhà vật lý người Mỹ John Wheeler đặt năm 1969.

Vào thời điểm này, Hawking đã sống hết hai năm kể từ ngày chẩn đoán được căn bệnh, mà sức khỏe chưa yếu đi nhiều lắm. Anh đang tìm đề tài làm luận văn tiến sỹ. Quan trọng hơn, anh chuẩn bị lấy vợ.

*

**

“Để cưới Jane, tôi cần phải có việc làm, để có việc làm, tôi cần bằng tiến sỹ.”

“Tôi đọc định lý của Penrose, định lý chứng minh rằng bất cứ vật thể nào bị suy sụp vào bên trong do lực hấp dẫn cũng sẽ hình thành một điểm kỳ dị. Tôi nhanh chóng nhận ra rằng nếu ta đảo ngược hướng của thời gian trong định lý của Penrose thì việc sụp đổ vào trong sẽ trở thành nở tung ra bên ngoài, các điều kiện (vật lý) của Penrose vẫn đúng, nó cho thấy một vũ trụ khá giống mô hình vũ trụ Friedmann (tức Big Bang).

“Định lý của Penrose đã chứng minh được bất cứ ngôi sao nào bị suy sụp vào trong sẽ phải tạo thành một điểm kỳ dị; lập luận ngược lại sẽ chứng minh được bất cứ vũ trụ đang giãn nở nào mà giống như mô hình Friedmann cũng phải bắt đầu từ một điểm kỳ dị.”

*

**

Với cảm hứng từ định lý của Roger Penrose về một điểm kỳ dị không-thời-gian nằm ở trung tâm một lỗ đen, Hawking đã hoàn thành bản luận văn xuất sắc của mình. Anh áp dụng định lý của Penrose vào kích cỡ lớn hơn: toàn bộ vũ trụ. Qua năm 1966, bản luận văn “Các điểm kỳ dị và hình học của không-thời-gian” của Hawking đã đoạt giải Adam dành cho các nhà toán học trẻ.

Trong ba năm cuối của thập niên 1970, Stephen và Jane sinh đứa con đầu lòng là con trai (1967); kết hợp với người đồng nghiệp lớn tuổi hơn và cũng là người thầy, nhà vật lý Roger Penrose, anh hoàn thành “định lý điểm kỳ dị Penrose -Hawking” (1968), và tiếp tục cùng Jane sinh đứa con thứ hai, lần này là con gái Lucy.

Công trình chung của Penrose và Hawking, cho thấy thuyết tương đối của Einstein áp dụng rất tốt ở các kích cỡ cực lớn như hệ mặt trời, ngân hà, hay toàn bộ vũ trụ lại bộc lộ khiếm khuyết lớn ở các điểm kỳ dị như Big Bang hay lỗ đen. Từ đó trong nghiên cứu tiếp theo của mình, Hawking đã sử dụng vật lý lượng tử, vốn chỉ áp dụng ở các kích cỡ cực nhỏ, vào việc nghiên cứu lỗ đen đã tạo ra được những đột phá lớn trong vật lý vũ trụ và lý thuyết hấp dẫn lượng tử.

Giả thuyết Kiểm duyệt vũ trụ

Penrose phát triển giả thuyết có tên gọi “kiểm duyệt của vũ trụ”. Ở phương tây thời đó, các đoạn bị kiểm duyệt bỏ trên các bài báo in sẽ bị bôi đen, bạn đọc biết đó là đoạn bị kiểm duyệt nhưng chịu không biết nội dung bị kiểm duyệt là gì. Các chỗ bị kiểm duyệt bị bôi đen như vậy thường là bộ phận nhạy cảm trên các hình ảnh cơ thể con người. Giả thuyết của Penrose được Hawking tóm tắt một cách hài hước: “Chúa không thích điểm kỳ dị khỏa thân.” Tức là điểm kỳ dị hình thành do suy sụp vì lực hấp dẫn chỉ xuất hiện bên trong những nơi như lỗ đen, là nơi mà các điểm kì dị bị giấu kín khỏi sự quan sát của những ai nằm bên ngoài đường chân trời sự kiện.”

*

**

Sau khi sinh Lucy, bệnh của Hawking nặng dần. Ngay cả việc leo lên giường để ngủ cũng mất rất nhiều thời gian. Trong một lần mãi mới leo được lên giường ấy, Hawking đã phát hiện ra một điều quan trọng. Anh gọi điện ngay cho Penrose và Penrose đồng ý với ý tưởng này.

*

**

Sau này, lúc đã rất già, mỗi khi Penrose đi giảng bài ông vẫn thường bị khán giả hỏi về Hawking. Ông giải thích rằng hồi đó hai người phải làm việc với nhau qua điện thoại. Giọng Hawking rất khó nghe, nếu nói về vật lý thì Penrose còn hiểu, khi nói về chuyện khác thì Penrose chịu, chả hiểu gì. Penrose cũng hay nói đùa là có hai Hawking, một Hawking trẻ luôn cứng cỏi bảo vệ lập trường của mình, rằng thông tin rơi vào lỗ đen sẽ biến mất; một Hawking già thì buông xuôi, đầu hàng trước sức ép của các nhà vật lý trẻ, và thay đổi lập trường của mình, rằng thông tin không bị mất trong lỗ đen mà được lưu trữ hoặc trả ngược ra bằng cách nào đó.

Có lẽ các nhà vật lý trẻ mà Penrose nói là ám chỉ đến Leonard Susskind và John Presskill. Susskind viết hẳn một cuốn sách tên Cuộc chiến lỗ đen về cuộc tranh luận dai dẳng này. Còn Presskill là người tham gia vụ cá cược nổi tiếng mà sau rất nhiều năm giằng co thì cuối cùng Hawking đã nhận thua Preskill. Preskill khi còn là sinh viên đã nổi tiếng với công trình về đơn cực từ của vũ trụ, là cái về sau dẫn đến thuyết “vũ trụ lạm phát” của Alan Guth. Hiện nay Preskill rất nổi với lý thuyết “thông tin lượng tử” và “tính toán lượng tử”. Một người khác cũng tham gia vụ cá cược này, ông đứng cùng phía với Hawking nhưng không chịu thua cược, đó là nhà vật lý Kip Thorne, người rất nổi tiếng qua bộ phim Interstellar và mới đoạt giải Nobel nhờ góp phần phát hiện ra sóng hấp dẫn.

*

**

Ý tưởng lóe lên trong đầu trong lúc leo lên giường đã dẫn Hawking đến việc anh áp dụng vật lý lượng tử vào nghiên cứu lỗ đen. Công trình này mang tên “Định luật hai của nhiệt động lực học lỗ đen”.

Nhiệt động lực học và entropy

Xuất hiện từ cuối thế kỷ 19, “định luật hai của nhiệt động lựchọc” phát biểu rằng entropy của một hệ cô lập sẽ luôn luôn tăng. Entropy là một đại lượng vật lý rất đặc biệt. Entropy được tính bằng công thức do Ludwig Boltzmann phát triển từ cuối thế kỷ 19 và được Max Planck hoàn thiện đầu thế kỷ 20 (tuy vẫn gọi là Boltzmann equation):

[image error]

trong đó S là entropy, kB là hằng số Boltzmann , ln là logarithm tự nhiên (trong hình là log) và V (trong hình là W) là thể tích. Tức là entropy tỷ lệ với thể tích (không gian 3 chiều) của hệ.

Đơn giản về toán học nhưng ý nghĩa vật lý của entropy rất sâu sắc và khó nắm bắt. Hawking viết “entropy là đại lượng vật lý đo cấp độ mất trật tự của một hệ”. Nếu một hệ bị bỏ mặc cho chính nó, entropy của nó luôn tăng, tức là càng ngày nó càng mất trật tự hơn.”

Hawking ví von entropy giống như bàn làm việc lúc đầu thì ngăn nắp, nhưng sau một hồi thì nó lộn xộn hết cả lên. Nếu ta sắp xếp cho nó gọn lại, trật tự hơn, thì cần tiêu tốn năng lượng và nỗ lực của bản thân, và việc tiêu tốn này làm giảm mức độ trật tự của năng lượng.

Hawking lập luận rằng mọi vật chất và năng lượng đi qua đường chân trời sự kiện của lỗ đen sẽ bị lỗ đen nuốt chửng, và diện tích bề mặt lỗ đen sẽ lớn dần lên.  Nếu một lượng vật chất có entropy lớn bị lỗ đen nuốt vào, tổng entropy bên ngoài lỗ đen sẽ giảm xuống, còn entropy bên trong lỗ đen sẽ tăng lên.

Từ đây, Hawking và một nghiên cứu sinh ở Princeton tên là Jacob Bekenstein đã tính được entropy của lỗ đen. Công thức này ngắn gọn như sau (SBH là entropy của lỗ đen, A là diện tích của bề mặt nằm trong có đường biên là chân trời sự kiện, k là hằng số Boltzmann).

[image error]

(c là tốc độ ánh sáng, h là hằng số Planck, là quantum, G là hằng số hấp dẫn, là gravity, ghép lại ta sẽ thấy trong một equation có cả có cả lượng tử và hấp dẫn, tức là quantum gravity: hấp dẫn lượng tử.)

Nếu chia h cho 2π, ta có ħ, công thức sẽ viết thành

[image error]

(về mặt hình thức, đây mới là equation được biết đến nhiều nhất của Hawking).

Công thức sẽ xuất hiện độ dài Planck nếu ta thay độ dài plank (lP) vào công thức

[image error]

[image error]

Trên đây là công thức nổi tiếng nhất của Hawking, nó có tên “công thức Bekenstein – Hawking”.

Trong công thức này ta thấy entropy của lỗ đen thay vì tỷ lệ với thể tích sẽ tỉ lệ với diện tích (mặt hai chiều) của bề mặt có đường biên là chân trời sự kiện của lỗ đen.

Nhưng nếu lỗ đen có entropy, Hawking lập luận tiếp, thì nó phải có nhiệt độ. Nếu nó có nhiệt độ, nó phải phát ra bức xạ. Lỗ đen phải phát xạ ra các hạt. Đến năm 1973 thì Hawking tính ra được nhiệt độ của lỗ đen. Phát kiến này của Hawking khi được công bố đã gây choáng cho giới vật lý đương đại. Hố Đen hóa ra không đen lắm.

*

**

Nhưng làm sao lỗ đen vốn chỉ nuốt tất cả mọi thứ, lại có thể nhả ra bên ngoài các hạt bức xạ. Hay nói cách khác, bằng cách nào các hạt ấy thoát ra khỏi lực hấp dẫn khổng lồ của lỗ đen.

Lời giải thích đến từ “phương trình Einstein E = mc2 và “nguyên lý bất định Heisenberg” trong cơ học lượng tử.

Khoảng chân không bên ngoài đường chân trời của lỗ đen không thực sự là “trống rỗng”. Nó vẫn có thể có trường hấp dẫn và trường điện từ. Trường này có cường độ và có tốc độ biến đổi cường độ. Cường độ và tốc độ biến đổi của trường tương đương với vị trí và vận tốc của một hạt. Và theo nguyên lý bất định Heisenberg, ta không thể nào xác định được chính xác đồng thời cả vị trí lẫn vận tốc của hạt. Tức là cường độ và tốc độ biến đổi của trường không thể cùng lúc bằng không. Nó sẽ phải khác không, tức là có thể sẽ có các thăng giáng lượng tử trong cái gọi là “chân không” này. Từ các thăng giáng này sẽ xuất hiện hiện các cặp hạt và phản hạt. Các cặp hạt – phản hạt này này trong vật lý được gọi là “ảo”, vì tồn tại rất nhanh, chúng sinh ra rồi lại hủy lẫn nhau (ví dụ hạt và phản hạt của ánh sáng hoặc trường hấp dẫn).

Vì cần phải có năng lượng để sinh ra các cặp hạt, nên trong mỗi cặp hạt và phản hạt sẽ có một hạt mang năng lượng dương, một hạt mang năng lượng âm. Sau khi được sinh ra, chúng tìm gặp nhau để tự hủy.

[image error]

Do lực hấp dẫn của lỗ đen cực kỳ lớn, chúng có thể hút một hạt ảo có năng lượng âm vào bên trong. Ngay khi vào bên trong, hạt ảo này trở thành hạt thực. Đối tác mang năng lượng dương của nó bơ vơ bên ngoài, không còn nhu cầu tự hủy và thoát khỏi vùng lân cận lỗ đen và đi vào nơi vô cực. Với người quan sát từ xa nhìn vào, các hạt thoát ra khỏi vùng lân cận của lỗ đen này giống như bức xạ do lỗ đen phát ra.

Ngày nay phát kiến này, được công bố hoàn chỉnh vào năm 1974, được biết đến với tên gọi “bức xạ Hawking”.

*

**

Giả thuyết ER=EPR

Bức xạ Hawking do sự hình thành của cặp hạt và phản hạt, trong đó một hạt bị hút vào trong lỗ đen, hạt còn lại bức xạ về nơi vô cực là tiền đề để gần đây Juan Maldacena và Leonard Susskind phát triển giả thuyết gây xôn xao giới vật lý lý thuyết: ER = EPR.

EPR, viết tắt của “nghịch lý Einstein–Podolsky–Rosen”, đề cập đến một hiện tượng bí ẩn bậc nhất của lượng tử: liên đới  lượng tử (hoặc còn được dịch là dính líu lượng tử). Trong đó hai hạt sinh đôi, ví dụ hạt ánh sáng sinh đôi, mỗi hạt sau khi ra đời bay theo một hướng khác nhau, thậm chí ngược nhau. Khi hai hạt ở rất xa nhau rồi, nếu ta đo lường một hạt và biết trạng thái lượng tử của nó, thì ngay lập tức ta biết trạng thái lượng tử của hạt kia. Cứ như là thông tin được truyền từ hạt này qua hạt kia ngay lập tức, tức là truyền nhanh hơn tốc độ ánh sáng. Mà theo thuyết tương đối của Einstein tốc độ ánh sáng vốn là bất biến, và không có gì có thể chạy nhanh hơn tốc độ này.

ER là viết tắt của “cầu Einstein–Rosen”.. Bằng cách sử dụng nghiệm của một lỗ đen tiêu chuẩn hình bình cổ dài với cổ bình bị cắt ngang và sáp nhập với một lỗ đen giống như thế nhưng đã bị xoay ngược lại. Ý tưởng này của Einstein và Rosen ngày nay được các nhà vũ trụ học hình dung như một cổng để kết nối hai vũ trụ khác nhau trong không-thời-gian. Ý tưởng này có tên gọi “cầu Einstein-Rosen” hay còn được biết với tên “lỗ sâu đục”. 

[image error]

Giả thuyết ER = EPR cho rằng liên đới lượng tử tồn tại được là nhờ hình thành một lỗ sâu đục giữa hai hạt của một cặp hạt, trong đó một hạt rơi vào lỗ đen, hạt kia đi về vô cực.

*

**

Vật chất và năng lượng là hai đại lượng vật lý có thể chuyển đổi qua lại với nhau, nhờ công thức của Einstein: E = mc2, trong đó E là năng lượng, m là khối lượng, c là tốc độ ánh sáng. Khi lỗ đen hút năng lượng âm vào bên trong, khối lượng của nó giảm đi, diện tích bề mặt lỗ đen nhỏ lại, entropy của lỗ đen giảm xuống (để bù vào entropy mà bức xạ mang đi). Hawking chứng minh được rằng khi khối lượng lỗ đen giảm xuống thì nhiệt độ tốc độ bức xạ tăng lên. Hiện tượng này ngày nay chúng ta gọi là “sự bay hơi của lỗ đen”. Lỗ đen bay hơi đến một lúc nào đó thì khối lượng của nó còn rất nhỏ. Cái gì sẽ xảy ra ở thời điểm đó thì chưa ai rõ, nhưng Hawking cho rằng lỗ đen sẽ kết thúc bằng một vụ phát nổ bức xạ (nay được gọi là “vụ nổ Hawking”), tương đương nổ một quả bom khinh khí (tức là rất nhỏ với quy mô của vũ trụ).

Một lỗ đen có khối lượng gấp vài lần khối lượng mặt trời sẽ có nhiệt độ khoảng 1 phần 10 triệu độ trên độ không tuyệt đối (tức là 0 độ Kelvin). Nhiệt độ bức xạ nền của vũ trụ khoảng 2,7 độ Kelvin, cao hơn nhiệt độ lỗ đen khá nhiều. Vậy nên lỗ đen sẽ hút vào nhiều hơn bức xạ ra. Nhưng do vũ trụ giãn nở nên nhiệt độ nền của vũ trụ sẽ giảm dần xuống, đến một lúc nào đó sự bay hơi của lỗ đen sẽ xảy ra. Sẽ cần một khoảng thời gian rất dài, hàng rất nhiều triệu triệu năm (1064 năm hoặc lâu hơn nữa), thì lỗ đen mới bay hơi hoàn toàn.

Giả thuyết Mô hình vũ trụ chu kỳ bảo giác (CCC)

Roger Penrose gọi quãng thời gian này là “kỷ nguyên nhàm chán”. Từ đây Penrose đề xuất một giả thuyết khá là điên rồ. Mỗi lần nói về thuyết này ông phải rào trước đón sau, rằng các nhà vật lý khác khi nghe đến thuyết này đều bảo rằng ông Penrose này già và lẩm cẩm quá rồi. Thuyết của Penrose có tên gọi “Mô hình vũ trụ học chu kỳ bảo giác (conformal cyclic cosmology, viết tắt là CCC). Theo đó vũ trụ có cuộc sống luân hồi. Vũ trụ như hiện nay sẽ trưởng thành và đến một lúc nào đó toàn bộ vật vật chất hiện đang rải rác khắp vũ trụ sẽ co cụm vào các lỗ đen. Lúc này entropy vũ trụ tăng đến cực đại và được chứa trong các lỗ đen (lỗ đen là nơi có entropy cực kỳ cao). Sau “kỷ nguyên dài nhàm chán”, các lỗ đen lần lượt bay hơi hết. Lúc đó vũ trụ chỉ toàn hạt ánh sáng, nó kết thúc để rồi tái sinh qua một điểm kỳ dị của Big Bang tiếp theo. Rồi cứ thế lặp lại. Mỗi một cuộc đời vũ trụ như vậy, Penrose gọi là một aeon.

[image error]

 

*

**

Trước khi có công trình đột phá của Hawking và Bekenstein, các nghiên cứu về lỗ đen chỉ giới hạn trong cơ sở của thuyết tương đối.Trong công thức tính entropy của lỗ đen, Hawking và Bekenstein sử dụng công cụ của vật lý lượng tử, trong đó diện tích bề mặt lỗ đen tính theo đơn vị độ dài Planck. Đây là đơn vị đo của lượng tử mà các nhà lý thuyết dây và hấp dẫn lượng tử cho là khoảng cách bé nhất của không gian, không thể chia cắt nhỏ hơn được nữa. Diện tích Planck rất nhỏ, một “Plank vuông” chỉ bằng 10-66 một xăng ti mét vuông.

Nếu vật chất rơi vào lỗ đen là một “trạng thái lượng tử” thì cũng có nghĩa đó là một lượng thông tin lượng tử rơi vào lỗ đen. Khi đã rơi vào bên trong lỗ đen, thông tin này sẽ bị hút về phía điểm kỳ dị. Khi chạm vào điểm kỳ dị, thông tin sẽ bị cuốn phăng về vô cực của thời gian. Thông tin sẽ bị mất vĩnh viễn. Điều này mâu thuẫn với quan điểm của vật lý lượng tử: thông tin luôn được bảo toàn, không thể nào phá hủy được bit thông tin. Đây chính là “nghịch lý thông tin lỗ đen”, hoặc còn được gọi là “nghịch lý Hawking”. Nghịch lý này dẫn đến vụ đánh cược nổi tiếng, cá cược từ năm 1991 mà đến năm 2004 Hawking mới nhận mình thua.

Giả thuyết  Vũ trụ toàn ảnh

Những người ủng hộ phe thắng cược phần nhiều là các nhà vật lý lý thuyết dây. Họ phát triển công trình của Hawking Bekenstein thêm một bước nữa. Năm 1997, nhà vật lý trẻ người Argentina tên là Joan Maldacena lần đầu tiên đưa ra “mô tả toàn ảnh của một vật thể có nhiều hơn ba chiều không gian (trong vật lý, do lỗ đen nằm trong không – thời gian nên các nghiên cứu lỗ đen phải làm việc với không gian bốn chiều hoặc nhiều hơn).

Những nhà theo “nguyên lý toàn ảnh” cho rằng toàn bộ thông tin (tức entropy) bên trong lỗ đen được mã hóa lên diện tích bề mặt lỗ đen. Giống như nếu ta chia nhỏ không gian trong một khán phòng hòa nhạc ra thành đơn vị thể tích Planck, thì tất cả các đơn vị này đều có thể được mã hóa lên mặt ngoài các bức tường của khán phòng. Mã hóa này làm bề mặt tường trở thành gồ ghề nhỏ li ti, và nếu biết cách ta có thể sử dụng nó như một tấm phim toàn ảnh (hologram). Hologram là một tấm phim phẳng (hai chiều) có bề mặt được chứa các thông tin đã mã hóa trong các rãnh gồ ghề rất nhỏ, nếu chiếu ánh sáng vào tấm phim này ta sẽ nhìn thấy hình ảnh khối (ba chiều) hiện ra. Hologram rất quen thuộc với chúng ta ở các tem chống hàng giả. Tức là nếu đứng bên ngoài khán phòng và chiếu ánh sáng phù hợp lên tường, ta sẽ thấy hình ảnh 3D của cả khán phòng bên trong. Hơn nữa, nếu các thông tin bên trong được quét giống như máy cộng hưởng từ quét não người, thì hình ảnh 3D hiện ra kia không chỉ là hình ảnh cái vỏ bên ngoài, mà chứa đựng cả nội dung bên trong.

Từ đó Leonard Susskind đưa ra các tính toán chi tiết hơn về một thế giới toàn ảnh (holographic world). Theo ông, do vũ trụ giãn nở liên tục, vũ trụ càng ở xa ta thì giãn xa với vận tốc càng cao. Ở một khoảng cách đủ xa, vũ trụ giãn nở nhanh hơn tốc độ ánh sáng, và bởi vậy ánh sáng từ đó không có cách nào chạy đến được với chúng ta. Như vậy khi ta nhìn ra vũ trụ xung quanh, nhìn xa hết cỡ cũng chỉ có thể quan sát tối đa được tới được một đường biên hình tròn gọi là chân trời vũ trụ. Ngoài đường tròn đó là một lượng thông tin khổng lồ, lượng thông tin ấy được mã hóa lên mặt phẳng bên trong đường tròn. Và thế giới mà ta đang sống chỉ là hình ảnh holographic hiện ra từ mặt phẳng ấy.

*

**

Trong những người ở phe không đồng ý với việc Hawking nhận thua cược có Sir Roger Penrose. Penrose có nhiều lập luận để biện minh cho việc thông tin bị mất hẳn khi rơi vào lỗ đen sẽ không vi phạm tính đơn nhất của vật lý lượng tử (tổng xác suất của mọi kết quả khả dĩ của hệ lượng tử đang tiến hóa phải luôn bằng một.) Đây cũng là một trong những lập luận cơ bản để Penrose xây dựng mô hình vũ trụ CCC kỳ lạ của mình.

Giả thuyết Tường lửa hố đen

Một nhà vật lý khác, Joseph Polchinski, người mới qua đời đầu năm nay ở tuối 63, đã khảo sát lại nghịch lý thông tin một lần nữa vào năm 2012. Khảo sát của Polchinski cho rằng bao quanh đường chân trời sự kiện là một bức tường lửa có nhiệt độ cực kỳ cao. Các lập luận và tính toán để đi đến kết luận này của Polchinski có những lập luận làm lung lay chiến thắng của phe thắng cược.  

*

**

Hawking kể rằng năm 1981 ông qua Moscow để dự một hội thảo về hấp dẫn lượng tử. Lúc này giọng nói của ông đã gần như không còn ai hiểu được nữa. Chỉ có người thân mới hiểu ông nói gì. Các bài giảng của ông được chuẩn bị trước và có người đọc lại. Khi tới Moscow ông mới nhận ra là chưa chuẩn bị trước. Vậy nên ông phải nói trực tiếp và một nghiên cứu sinh của ông nhắc lại cho khán giả hiểu. Cách làm này vô tình khiến ông có cảm xúc trong việc tương tác với thính giả. Có lẽ đây là cảm hứng để ông viết cuốn sách dành cho bạn đọc phổ  thông mà sau này cực kỳ nổi tiếng, cuốn Lược sử thời gian. Trong chuyến đi tới Moscow này, Hawking đã “phát hiện” được một nhà vật lý trẻ người Nga, Andre Linde, người sau này chuyển sang Mỹ làm việc và thành công với mô hình vũ trụ lạm phát (cùng với Alan Guth).

Giả thuyết Vũ trụ không mặt biên

Hai năm sau, năm 1983, Hawking và James Hartle đề xuất giả thuyết “Hàm sóng của vũ trụ” theo đó ở vũ trụ không có mặt biên. Vũ trụ là một điểm kỳ dị trong không – thời gian ngay trước Big Bang, về mặt toán học nó không có đường biên (bề mặt, bao bọc bên ngoài) của cả thời gian lẫn không gian. Thời gian như ta nhận thức được hiện nay, chỉ đột ngột sinh ra sau khi vũ trụ kết thúc kỷ nguyên “thời gian Planck”. (Thời gian Plank là khoảng thời gian ngắn nhất theo vật lý lượng tử và không thể chia cắt nhỏ hơn nữa.) Theo giả thuyết này, vũ trụ hiện nay giống như bề mặt của của một quả bóng bay đang được bơm căng dần lên. Các thiên hà nằm trên bề mặt quả bóng và do quả bóng đang căng lên các thiên hà cũng sẽ giãn xa nhau ra.

Hai năm sau nữa, năm 1985, sau một ca phẫu thuật, Hawking mất giọng nói hoàn toàn và phải dùng máy tính để trợ giúp.

*

**

Stephen Hawking sinh ngày 8 tháng Giêng năm 1942, đúng vào ngày mà trước đó 300 năm Galile Galileo qua đời. Hawking khá thích chi tiết này và có nhắc đến trong cuốn sách nổi tiếng của mình.

Ngày 14 tháng 3 năm nay, đúng vào ngày của số Pi (Pi Day), và là sinh nhật lần thứ 139 của Einstein, nhà vật lý lỗ đen Stephen Hawking đã bay hơi về nơi vô tận. Nhưng chắc chắn các bức xạ vật lý của ông sẽ không bao giờ bị mất, nó sẽ tồn tại mãi trong kiến thức của vũ trụ học hiện đại và trong những trang sách giáo khoa. Đây có lẽ là lý do mà Hawking cuối cùng đã chịu phần thua trong vụ cá cược dai dẳng và nổi tiếng khắp thế giới.

 

Hawking nói về thuyết lượng tử

 “Tôi không đòi hỏi một lý thuyết phù hợp với thế giới thực vì tôi không biết lý thuyết đó là gì. Thế giới thực không phải là một đại lượng mà ta có thể kiểm tra bằng mấy mấu giấy quỳ tím. Tất cả những gì tôi quan tâm là một lý thuyết có thể dự báo kết quả của các phép đo.”

Miếng ăn

Hôm nay trên mạng lan truyền một cái ảnh, không rõ thật hay fake, chụp các đồng chí anh nuôi bày bếp dầu nấu ăn trên boong chiến hạm, dưới đít tên lửa.

Miếng ăn, là miếng tồi tàn. Miếng ăn, là miếng nhục. Không phải tự nhiên các cụ nói vậy.

Dân mình, thấy miếng ăn ở khắp mọi nơi.

Các sự kiện quan trọng nhất trong đời một con người, vui hay buồn, đều phải có ăn: ăn cưới, ăn sinh nhật, ăn đám ma, ăn giỗ.

Các lễ lạt trong năm, có tính chu kỳ, năm nào cũng có và cũng ăn: ăn rằm, ăn Tết.

Ngày xưa ra đường làng gặp nhau, thay câu chào, là câu hỏi: ăn chưa, cơm nước gì chưa?

Nói chuyện liên quan đến mồm, có ăn đã đành: ăn nói. Mặc quần áo cũng phải dính đến ăn: ăn mặc. Học hành cũng phải ăn: ăn học. Thậm chí chuyện chịch nhau cũng phải có ăn: ăn nằm.

Làm chính trị đỉnh cao, quan trọng là kiến quốc, thì hóa ra cũng cốt ở cái ăn: Giữ chùa thờ phật ăn …oản.

Đi làm thì không nghĩ đến rèn luyện chuyên môn, đạo đức nghề nghiệp, đầu chỉ nghĩ đến ăn: thợ may ăn vải, thợ vãi ăn hồ.

Nhà chùa, sư sãi, lẽ ra phải nhịn ăn, nhưng ăn rất khiếp.

Những nghề lẽ ra phải tránh ăn, như giáo viên, bác sĩ, cũng lăn vào mà ăn.

Miếng ăn nặng thế, triều đình tranh ăn của nhau, công lực ăn của dân, làm nghề nào ăn nghề ấy. Đến cái tàu chiến tối tân cũng thành cái bếp để nấu cỗ để ăn.

Khi nào dân mình hết thèm cái ăn, không còn nhăm nhăm nghĩ đến cái ăn, miếng ăn trở thành miếng bình thường chứ không phải miếng tồi tàn, có lẽ lúc đó nước mình mới khá được.

Cám ơn các đồng chí anh nuôi, dép tổ ong, trên tàu tên lửa, đã làm V.Rohto làm sáng mắt rất nhiều dân đen, như bọn chúng em.

Chú thích: Cái bếp trong hình của nhà hàng tiệc cưới hộ vệ tên lửa không phải bếp gas, mà là bếp dầu đun kiểu gas. Bếp này rất phổ biến ở các quán ăn bình dân trong nam, nhất là quán lớn, xào nấu nhiều, hoặc ở các nhà chuyên nấu tiệc. Nguyên lý hoạt động của bếp này là bơm dầu (thể lỏng) vào bình chứa có áp suất cao (giống cái bình gas). Từ bình, dầu đi qua ống hóa khí, đi vào cốc phun sương, rồi cháy vào bếp. Bếp kiểu này hơn bếp dầu kiểu cũ là hiệu suất nhiên liệu cao, không bị muội, nhiệt độ cháy cũng rất cao, cỡ 1300 độ C (lửa màu xanh, bếp kiểu cũ chắc chỉ vài trăm độ, lửa màu đỏ, ai biết quang phổ màu sẽ ước lượng được). Cám ơn các đồng chí anh nuôi đi dép tổ ong, đã promote sản phẩm này. Bếp dầu hitech đun đít tên lửa hitech. Hy vọng bếp của các đồng chí không phải hàng tàu.