Scott H. Young's Blog, page 21

How Do We Learn Complex Skills? Understanding ACT-R Theory

How do we learn to perform complex skills like programming, physics, or piloting a plane? What changes in our brain allow us to perform these skills? How much does learning one thing help us learn something else?

These are hard questions. Most experiments only attempt to address narrow slices of the problem. How does the schedule of studying impact memory? Is it better to re-read or retrieve? Should you practice a whole skill, or build up to it from its parts? These don’t directly address the big questions.

This is what makes John Anderson’s ACT-R theory so ambitious.1 It’s an attempt to synthesize a huge amount of work in psychology to form a broad picture of how we learn complicated skills. Even if the theory turns out not to be the whole story, it helps illuminate our understanding of the problem.

First, A Note on Scientific Paradigms

Before I get to explaining ACT-R, I need to step back and talk about how to think about scientific theories, in general.

All scientific theories are built on paradigms. A paradigm is an example that you take as central for describing a phenomenon. Newton had falling apples and orbiting planets. Darwin had the beaks of finches. Obviously, Newton didn’t restrict his theory to tumbling fruit, nor Darwin to a few island-dwelling birds. Yet, these were the examples they used to lay the foundations for their broader theories.

Nowadays, we take for granted that mechanics and evolution are Science, and thus their original paradigm cases are largely historical footnotes.2 We can ignore their origins and simply focus on applying the theory.

Theories of the mind aren’t like this. Nobody believes we’ve found some unified theory that fully explains how the mind works. Yet we know a lot more than nothing. Scientists have collected mountains of evidence that sharply constrain any valid theory of the mind. But minds are complicated, and there are still a lot of possible theories that could fit.

With this in mind, what does ACT-R take to be its paradigm case for cognitive skill? ACT-R focuses on problem-solving, particularly in well-defined domains like algebra or programming. Specifically, its focus is on intellectual skills. ACT-R does not account for how we move our bodies nor how we transform input from our eyes and ears to make sense of the problem.

This paradigm might not seem very representative. Certainly, most of human experience isn’t like programming LISP. Yet a good paradigm doesn’t need to be prototypical of the phenomena it tries to model. In fact, often the opposite is true, with the best paradigms being unusual because they lack the messiness of more typical situations. Newtonian mechanics had to overcome the fact that we’re immersed in an atmosphere where friction is ubiquitous, and most objects eventually come to rest. Darwin needed the peculiar environment of the Galapagos where finches would adapt to unique niches in relative isolation.

Within this paradigm, ACT-R makes some impressive predictions and manages to account for a huge body of psychological data. Therefore, I think it’s worth understanding seriously if we want a better picture of how we learn things.

ACT-R Basics: Declarative and Procedural Memory Systems

ACT-R argues that we have two different memory systems: declarative and procedural.

The declarative system includes all your memories of events, facts, ideas and experiences. Everything you consciously experience is part of this system. It contains both your direct sensory experience and your knowledge of abstract concepts.

The procedural system consists of everything you can do. It includes both motor skills, like tying a shoelace or typing on a keyboard, and mental skills, like adding up numbers or writing an email.

ACT-R explains complex skills as an ongoing interaction between these two systems. The declarative system represents the outside world, your inner thoughts and intentions. The procedural system acts on those representations to make overt actions or internal adjustments that move you closer to your goals.

Why two separate systems? A single system would be simpler. But there’s an impressive range of evidence arguing that these systems are distinct in the brain:

Amnesiacs can learn through the procedural system, but not the declarative system. They can learn to perform new tasks, but afterward, they have no memory of having been taught.Priming experiments only work with the declarative system, and not the procedural. For example, presenting the word “computer” speeds up how quickly people can access computer-related memories. Still, it does not make them any faster at using a computer.Procedural memory is unidirectional. This is why saying the alphabet forward is so much easier than saying it backward. To go backward you need to produce the letters going forward, rehearse them in your head so that a declarative representation is active, and finally manipulate them to reverse the order.Declarative memory shows fan effects. In declarative memory, links between nodes go both ways, and either node can access the other. However, a node with many outgoing links doesn’t link to any particular one of them strongly. For example, a picture of a beagle makes it easy to recall “dog,” but the word “dog” likely won’t cause you to recall the picture of a specific beagle.Neuroscientific studies suggest different locations for the two systems. The hippocampus and associational cortices play pivotal roles in declarative memory. In contrast, the procedural system seems to rely on subcortical structures such as the basal ganglia and dopamine networks.The Declarative System

The basic unit of declarative memory is the chunk. This is a structure that binds approximately three pieces of information. The exact contents will vary depending on the chunk, but they’re assumed to be simple. “Seventeen is a number” might be an English description of a chunk that has three elements: [17][IS A][NUMBER].

Since chunks are so rudimentary, how do we understand anything complicated? The idea is that, through experience, we connect these chunks into elaborate networks. We can then traverse these networks to get information as we need it.

The declarative memory structure is vast, but only a few chunks are active at any one time. This reflects the distinction between conscious awareness and memory. When we need to remember something, we search through the network. For practiced memories, this is relatively easy as most related ideas will only be a step or two away. For new ideas, this is much harder since they’re less well integrated into our other knowledge and therefore require more effortful search processes.

How do nodes get activated? There are three sources:

First, you perceive things from the outside world that automatically activate nodes in memory. (Perhaps you see a dog, and some set of dog-related nodes get activated.)Second, you can rehearse things internally to maintain them in memory. Think of trying to remember someone’s phone number to write it down. You might repeat it to yourself to “refresh” the auditory experience that is no longer present.Third, nodes can activate connected nodes. This is what happens when one thought leads to another. The exact details of this spreading activation mechanism is not entirely clear in ACT-R. But Anderson assumes that which chunks tend to be active is related to their likely usefulness in the situation.

The declarative system, with its vast hidden network of long-term memory and briefly active nodes corresponding to our conscious awareness is impressive. In order to solve problems, we use this system to make decisions about what to do next. But, according to ACT-R, it’s also inert. Something else must transform it into action. That’s where the procedural system comes in.

The Procedural System

The basic unit of the procedural system is the production. This is an IF -> THEN pattern. To illustrate, a production might be “IF my goal is to solve for x, and I have the equation ax = b, THEN rewrite the equation as x = b/a.”

Think of productions like the atomic thinking steps involved in solving a problem. Whenever you need to take an action or make a decision, ACT-R models this as a production activating.

Unlike the sprawling, interlinked declarative memory, productions are modular. Each one acts as an isolated unit that is learned and strengthened independently. Solving complex problems involves more productions than simple puzzles, but the basic ingredients are the same.

For each active representation in declarative memory, many different productions compete to find the best match for the current situation. When a production matches an active representation in declarative memory, and the expected value from executing this production exceeds the expected cost of either taking a different action or waiting, it triggers. The action is taken, the state of the world (or your internal mental state) changes and then the process repeats itself.

If you repeat a sequence of actions many times, this sequence can be consolidated into a single production. Thus, only one production has to be activated to execute the entire series of mental steps from start to finish. While this is faster, it is also less flexible. With time, this can result in skills that are less transferable to new situations as you’ve automated specific solutions for specific problems, rather than implementing the general procedure from scratch each time.

How ACT-R Claims You Solve Problems

Let’s summarize the overall process of reasoning presented here:

You form a representation of the problem in your declarative system. This representation combines your current sensory experience with long-term memory and short-term rehearsal buffers.Productions compete with each other based on this current representation. Which one wins depends on how well it matches with an active chunk in declarative memory and the benefit you expect from taking that action.As each production is executed, it changes your present state. You either take action in the outside world, which will change your declarative representation via sensory channels, or the production changes your internal state.The process repeats itself until the problem is solved.How Do We Acquire Skills?

In the ACT-R theory, learning skills is thought to be a process of acquiring and strengthening productions.

Initially, productions are learned via analogy. We search our long-term declarative memories for a similar problem. Then we try to match this to our current representation of the problem. When we have a match, we create a production.

ACT-R argues that we don’t learn by explicit instruction, only by example. When we appear to learn via instruction, we first generate an example based on the instruction and then use this example to create a new production.

Once created, productions are strengthened through use. Every time a production is used to solve a problem, it becomes more likely to be chosen again in similar circumstances. The strengthening process is incredibly slow. This is why it can take so much practice to be good at complicated skills. Getting all of the productions to fire fluently requires enormous repetition and fine-tuning.

According to ACT-R, the only thing that matters for solving a problem is reaching the solution, not how you got there. Mistakes in the process waste time and do not contribute to learning. Thus Anderson advocates for intelligent tutors who immediately correct mistakes in the process of solving a problem.

Transfer of Learning

ACT-R makes robust predictions about learning and transfer that are supported by quite a bit of data.

A key prediction is that the amount of transfer we predict between two different skills will depend on the number of productions they share in common. How well does it do?

The following graph is reproduced from Anderson’s Rules of the Mind. The prediction is that transfer should be linear in the number of productions. This is exactly what we see.3 To my mind, this is some of the best evidence that ACT-R, or something like it, accounts for the transfer of cognitive skills.

However, transfer is somewhat better than ACT-R predicts. The fit is linear, but it starts around 26%. If skills truly had no shared productions, the theory suggests the fit should start at 0%. Anderson argues that this is probably because their model of skills omitted some productions. For instance, there may be some productions involved in using the computer that transfer between every task that uses the same system.

What about more complicated skills? ACT-R argues that more abstract, higher-level skills should transfer better between situations because the underlying productions are preserved. So the skill of designing an algorithm should transfer between different programming languages because the algorithm is the same in each case, even if the skill of writing the syntax to code the algorithm won’t.

What about knowledge and understanding? ACT-R has less to say here. The types of puzzles used to test ACT-R theory tend not to require a lot of background knowledge. Since the declarative part of learning is relatively quick in the demonstrations studied, it doesn’t dominate the transfer situation. For knowledge-rich domains like law or medicine, there may be different patterns of transfer as properly activating the declarative memory system becomes the most time-consuming part of acquiring a skill.

Over a century ago, Edward Thorndike proposed that the only transfer we could expect between skills was due to them containing identical elements. ACT-R is essentially a revised version of this theory, arguing that the elements Thorndike sought are productions.

Implications of ACT-R

Nearly a year ago, I started digging into research on transfer. It turned out to be a much deeper and more interesting question than I had initially realized. Understanding what knowledge transfers depends critically on the answer to the question, “what is actually learned through experience?”

ACT-R makes a bold claim regarding this central question: The basic units of skill are productions. Practice generates new productions and strengthens old ones. Skills transfer to the degree to which these productions overlap.

There are a few general implications we can tease out:

Most skills will be highly specific. Chess strategy doesn’t transfer to business strategy because they have almost no productions in common. A microscopic analysis of any two skills should, in principle, tell us how much transfer is possible.Transfer should look smaller on tests of problem solving than on tests of future learning. To solve a problem you need all of the productions. Possessing half of the productions doesn’t help because you’re missing steps needed to move forward. However, having half of the productions will make learning twice as fast, because you don’t have as many new ones to acquire. School frequently fails to teach all of the skills needed for real-world performance. This can be embarrassing when you measure people’s proficiency on problems. But the result needn’t be gloomy: with further training, those people would likely quickly learn skills that use the same components.Practice makes perfect, but many types of practice can be wasteful. Anderson favors intelligent tutoring systems that immediately correct students when they make a mistake. Whether computers are up for this task is an open question, but human tutors are one of the most effective instructional interventions known.Complicated skills have simple learning mechanisms. Although the description of a production system may look complicated, it’s dead simple compared to the diversity of skills we regularly perform. Positing simple mechanisms suggests that even the most complex performances can, in theory, be broken down into learnable parts. The only difficulty is investing all the time needed to learn them.

In the next essay, I will examine Walter Kintsch’s Construction-Integration model. Whereas ACT-R uses defined problem-solving as its central example, CI delves into the process we use for comprehending text as its paradigm. Both models have considerable overlap, which is reassuring in light of the volume of psychological data. Still, they have some interesting contrasts as well.

The post How Do We Learn Complex Skills? Understanding ACT-R Theory appeared first on Scott H Young.

Life of Focus Is Now Open

Life of Focus, the three-month training program I co-instruct with Cal Newport, is now open for a new session. We will be holding registration until Friday, February 11th, 2022. Check it out here:

https://www.life-of-focus-course.com

This course aims to help you achieve greater levels of depth in your work and life. How would it feel to have more time and energy for the things that really matter to you?

We split the course into three, one-month challenges. Each challenge is a guided effort to help you establish and test new routines, alongside specific lessons to deal with issues you might face. Those challenges are:

Establishing deep work hours. We all know we could get a lot more done with less stress if we had more time for deep work, but actually achieving this regularly can be tricky. The first month focuses on finding and making the subtle changes you need to get in more deep work—without working overtime.Conducting a digital declutter. Technology can be great, but it can also make us miserable. Having endless distraction within arms reach, it’s hard to engage in meaningful hobbies and have deeper interactions with our friends and family. This month helps you cultivate a more deliberate attitude to the digital tools in your personal life.Taking on a deep project. In the final month, we’ll reinvest the time we’ve created at work and at home in a project that engages you in something meaningful. This can be learning something new or actually creating something instead of just passively consuming. Lessons will help you learn how to integrate deep hobbies into your busy life.

Life of Focus may be the most popular course we’ve run—and one in which students have reported some of the strongest results. This is because Life of Focus is action oriented—not just consuming information, but making sure you form lasting changes to your life.

Registration is open now. If you’re interested, click below. Registration is only open until this Friday:

https://www.life-of-focus-course.com

The post Life of Focus Is Now Open appeared first on Scott H Young.

The Structured Pursuit of Depth

This is a guest lesson from my Life of Focus co-instructor, Cal Newport. In anticipation of a new session of our popular course, he decided to share some of his experiences building a deep life. Enjoy!

Early in the pandemic, driven by the dislocation that characterized the moment, I began writing about a topic I quickly came to call “the deep life.” Though the name was new, the underlying idea was not, as few impulses are more ancient than the pursuit of a richer existence.

The instinct when talking about this topic is to resort to the lyrical: tell motivating stories, or present scenes that spark inspiration. This instinct makes sense. The deep life is nuanced and complicated. It cannot be fully reduced to practical suggestions or a step-by-step program.

And yet, this is exactly what I attempted.

Less than a month after my original post on the topic, I introduced a “30-day plan” in which you focus on four main areas in your life, identifying for each one habit to “amplify” and one behavior to “reduce.” I even presented a sample table to demonstrate the plan in action:

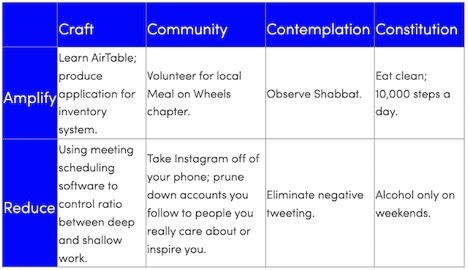
Later that spring, on my podcast, I elaborated this idea into something I called the “deep life bucket strategy,” which presented a two-stage process for systematically overhauling your life.

Then, over that summer, Scott Young and I completed a new online course called Life of Focus (which, I should probably mention, opens again next week to new students), that included a major module on engineering more depth into your regular routine.

To explain my contrarian shift toward the pragmatic in my treatment of this topic, I should first note that I agree that the deep life cannot be fully reduced to a system. But I’ve also come to believe that systems still have a role to play in this context, as they can help you understand this goal better fleeting moments of inspiration. This idea is familiar in theological circles. Many religions believe that although the concept of God cannot fully be understood by the human mind, and that certain ritual practices, such as daily prayers, can spark intimations of the divine that cannot be captured in third-person description.

Something similar (though less grandiose) is at play with systematic attempts to pursue the deep life. Identifying buckets, or amplifying habits, cannot by themselves guarantee a life well-lived. But they do require you to take focused action toward this objective, and it’s in this action — including the missteps and surprises — that you gain access to a richer comprehension of what this goal means to you, and what you need to achieve it.

The deep life cannot be reduced to concrete steps. But without concrete steps, you’ll never get closer to this goal.

===

Scott here. Next week, Cal and I will be reopening Life of Focus for a new session. Life of Focus is a dedicated, three-month training program for improving your depth at work and at home, letting you spend more time on the things that really matter. We hope to see you there!

The post The Structured Pursuit of Depth appeared first on Scott H Young.

Why Don’t We Use the Math We Learn in School?

How much of the math you’ve learned in school do you use in everyday life? For the majority of people, the answer is surprisingly little.

This question is at the heart of the problem of transfer of learning—how we apply what we’ve learned to new problems and situations. As readers will note, I’ve spent the better part of the last year digging into the research surrounding this topic. Why we fail to use the math we’ve learned may seem trivial, but it reveals fundamental principles of learning.

Before I get into the explanations, let’s start by examining the evidence for my assertion that most people don’t use the math they’ve learned in school.

Evidence for the Failure to Use Math

Casual observation tells us that most people don’t use math beyond simple arithmetic in everyday life. Few people make use of fractions, trigonometry, or multi-digit division algorithms they use in school. More advanced tools like algebra or calculus are even less likely to be brought out to solve everyday problems.

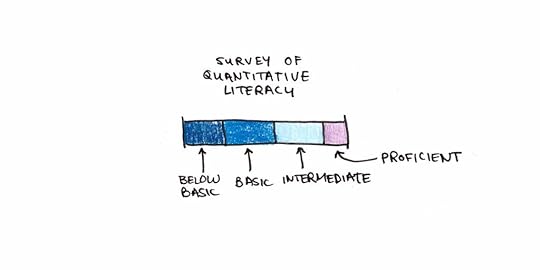
Research on the overall population’s use of math bears this out. A 2003 survey of 18,000 randomly selected Americans gave a battery of questions that embedded mathematics problems into situations they might encounter.1 The survey authors created the following scale to rank Americans’ quantitative abilities:

Below Basic – Add up two numbers to complete an ATM deposit.Basic – Calculate the cost of a sandwich and salad using prices from a menu.Intermediate – Calculate the total cost of ordering office supplies using a page from an office supplies catalog and an order form.Proficient – Calculate an employee’s share of health insurance costs for a year using a table that shows how the employee’s monthly cost varies with income and family size.

Only 13% of Americans scored as “proficient,” while over half were “basic” or “below basic.”

Anthropological studies support the observation that most people fail to use higher math. Jean Lave conducted fieldwork observing the mathematics people used in everyday life. She found that people often performed reasonably well in real-life settings, but their performance dropped when the same problems were expressed in the form of a test.2

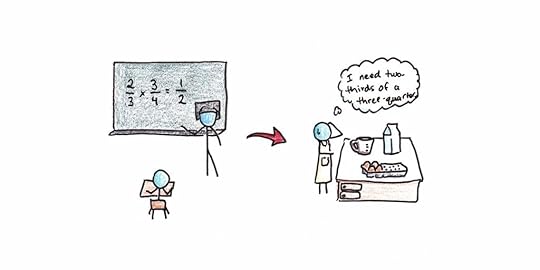
In one frequently cited episode, an individual was trying to calculate 2/3rds of 3/4 cups of cottage cheese. Instead of applying learned math (multiplying fractions would give the easily-measurable answer of 1/2 cup), the person scooped out 2/3rds of a cup, made a rough circle on the table, and cut out a quarter.

My argument is not that nobody learns math or that math is useless. Clearly, some people learn math very well and apply it in everyday problem-solving settings. People in professions that rely on math are more likely to apply it both in and outside of work. The question is why most people don’t, in spite of spending many years practicing it.

Why Do People Fail to Use Math

I see three explanations for the failure to use math in everyday life:

Most people don’t learn math well enough to use it effortlessly.We learn school math but fail to translate real problems into a format where we can apply our math knowledge.Most higher math isn’t useful for everyday problems.Explanation #1: Most People Don’t Learn Math Well Enough to Use It

The first argument would allege a failure of education. People don’t use math because they were never taught it thoroughly enough to use it properly.

There’s a lot in favor of this argument. One of the major barriers to using a skill in real life is automaticity. We tend to find the least-effort solution to our problem. If struggling through a math problem is hard for you, you’ll find a different way to solve it that doesn’t rely on math.

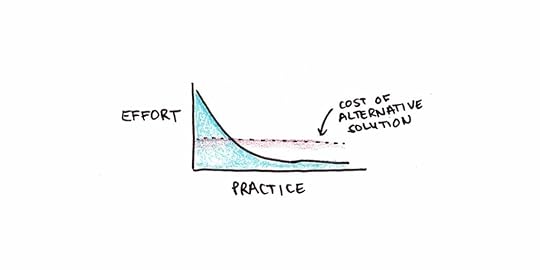
This seems the best explanation for the cottage cheese incident earlier. Suppose the person was fluent with basic fraction facts. In that case, the mental answer of “2/3 x 3/4 = 6/12 = 1/2” is much less work than scooping out cottage cheese and manipulating it manually.

A lack of automaticity may explain the difficulty people had with the quantitative questions in the survey. Their math wasn’t easily accessible, which led them to make mistakes in the reasoning tasks.

Explanation #2: Most People Don’t Know How to Translate Real-Life Situations into Math Problems

The second argument is a little different. It argues that people may develop competence in math classes, but they struggle to translate real-life problems into a format where they can use their mathematics knowledge.

This seems most apparent in the case of applying algebra. Students struggle with algebra, but they particularly struggle with word problems. Yet, the equivalent real-life problems are typically much harder than word problems.

Every word problem takes place in an algebra class, so you know that algebra will be part of the solution. Further, teachers rarely give impossible problems, so you know that your prior knowledge should be sufficient to solve it. Finally, word problems end up being stereotyped formats (trains leaving various cities) which you can use as a cue to identify which type of problem it is. Extracting an algebraic representation of real-life problem situations is typically much harder.

I can recall an example of this in our business. Where we’re located, sales tax gets added to the stated purchase price. So if we had a $10 product with 10% sales tax, you’d charge the customer $11 and set aside $1 for the government. However, our software at the time couldn’t add the sales taxes, so we had to calculate how much to send the government afterward.

Without thinking much about it, the person I was working with said we need to remit 10% of our sales. Except that isn’t right. If he had applied algebra, the problem would have been: amount collected = actual sales + actual sales * 10%. Taxes owed would then be the amount collected divided by 1.1 multiplied by 10%. For $10, that would be $0.91.

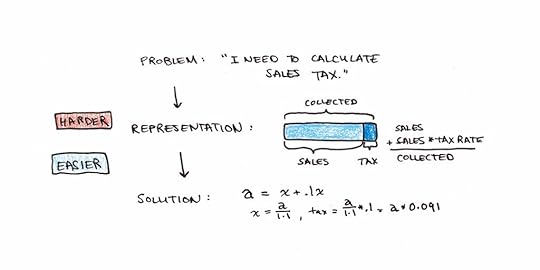
Stated as an algebra equation, the person immediately saw the correct answer. Even telling him the basic idea, that the tax amount needs to be 10% bigger than the amount leftover, got the right solution immediately. The trick was recognizing that algebra needed to be applied.

From this perspective, what people struggle with is not doing math, but recognizing where and how to apply math to real problems.

Explanation #3: Math Isn’t That Useful for Everyday Problems

A third explanation is that math is overrated as a solution strategy for problems outside of exacting, quantitative disciplines. The person measuring cottage cheese managed to get the correct answer without multiplying fractions.

There’s an interesting split in perspective on this issue when I’ve asked people about it. People who are good at math point out that it’s obviously useful and the only way to get correct answers to quantitative problems. People who are bad at math tend to discount math’s relevance to everyday life.

The math-supporters would argue that people’s failure to see the relevance of math to everyday life is due to their inability to use it. Knowledge determines what solution strategies are available to you. If knowledge is missing (as in explanation #2) or is insufficiently effortless (as in explanation #1), then you tend to view using it as expensive and unnecessary.

The math-detractors would argue that there’s a sunk-cost bias on behalf of the math experts. They’ve invested a lot of effort into learning math well. Thus, they naturally see it as the “correct” way to solve most problems, even if many problems can be solved in other ways.

Everyone values knowledge they have mastered, and tends to dismiss knowledge they haven’t as irrelevant. There’s probably bias on both sides.

I tend to lean in favor of the first group, but that might be my bias from having learned a lot of math!

How Can We Make Math More Useful?

Setting aside explanation #3 for a moment, let’s argue that the math-supporters are indeed correct about its general utility. What could we do to make math easier to apply?

There seem to be a few options:

More drill and practice with math. More time spent drilling and practicing math makes it more available for effortless calculations. Failure to sufficiently master academic subjects results in a lot of knowledge that is inert for practical purposes.More practice with interpreting problem situations. Many students are only taught math as symbol manipulation. Less instruction is focused on identifying situations where it might be useful. We need to give students more training in noticing and converting everyday situations into the math problems they know how to solve.Give real-life challenges that require math. Ultimately, skills and knowledge are sustained by usage. If you don’t have any genuine problems that require a skill, you begin to forget it. The reason people in STEM professions maintain sharp math skills is because they need them to be sharp.

Mathematics can be a stand-in for nearly any academic subject. In all cases, to have useful skills, you need a combination of automatic skill, problem identification and interpretation, and sustaining real-world usage. Anything less and knowledge learned fails to leave the classroom.

The post Why Don’t We Use the Math We Learn in School? appeared first on Scott H Young.

New Research Shows I Was Right About Watching Lectures Faster

A new paper argues that watching video lectures at 2x the speed has minimal costs to comprehension. From the abstract:

“We presented participants with lecture videos at different speeds and tested immediate and delayed (1 week) comprehension. Results revealed minimal costs incurred by increasing video speed from 1x to 1.5x, or 2x speed, but performance declined beyond 2x speed. … increasing the speed of videos (up to 2x) may be an efficient strategy, especially if students use the time saved for additional studying or rewatching the videos…”

When I was doing the MIT Challenge, people often scoffed at my strategy of watching lectures at 2x (or even 3x speed). This enabled me to watch all the lectures for a full-semester class in as little as two days. Yet, I frequently heard from onlookers that this would make comprehension impossible.

However, now that podcasts are popular, it’s become common knowledge that you can listen at an accelerated pace without suffering significant comprehension losses. Still, it was nice to see research addressing this question with academic materials.

Speculations on Why This Strategy Works

Speeding up lectures doesn’t seem to severely impact comprehension, yet speed reading probably doesn’t work. What’s the difference?

For starters, lectures proceed at a fixed pace. Reading has always been variable speed—you speed up when your comprehension is high and slow down when it is low. Speed reading advocates claim that you can force the pace higher than feels comfortable, but this involves a comprehension trade-off. The higher speed might be beneficial when you only need the gist, but in those cases it’s better to call it skimming rather than reading.

For speaking, however, our ability to comprehend is generally much faster than a comfortable speaking pace. Additionally, generating speech is probably more demanding than listening. The public speaking advice to speak slower is generally true: if you speak slower, you can be more articulate and careful in your choice of words which makes you sound smarter. But take a recording of that speech, and you can probably speed it up with minimal consequences.

Why Do Hard Classes Feel Too Fast?

If this is true, why did so many people balk at my original suggestion? I think the issue with hard classes isn’t the rate of speech but the amount of background you need to already have to get a full understanding. Hard classes are hard because the speaker glosses over elements that are important for understanding, creating inferential gaps. Knowledgeable students keep pace without problem, but poorer students get lost.

Unfortunately, if there are inferential gaps, simply slowing down the rate of speech may not help much. If you don’t understand, you need more explanation, not the same patchy explanation done more slowly.1

The irony is that, without a good explanation, chances are you would need the lecture much slower than normal speed to understand. The Feynman Technique is a tool that can help fill in gaps, but this is generally only useful when the gaps are minimal. If you have no understanding whatsoever, it’s usually more efficient to seek alternate explanations of the same idea.

Still, more than ten years after the MIT Challenge, I’m pleased to see research bear out something that I felt intuitively had to be right.

The post New Research Shows I Was Right About Watching Lectures Faster appeared first on Scott H Young.

The Science of Achievement: 7 Research-Backed Tips to Set Better Goals

Setting goals can transform your life. Goals can help you get in shape, improve your finances, learn a new language, or finally launch that business.

But goal-setting can also leave you miserable. Burnout, stress and disillusionment are high on the list of potential side effects.

The crucial difference between success and burnout often comes down to how your goals are designed. Done wisely, setting goals can be a positive experience—not just successful, but life-affirming. Here are seven research-based suggestions to help you design better ones.

1. Aim for Hard, but Believable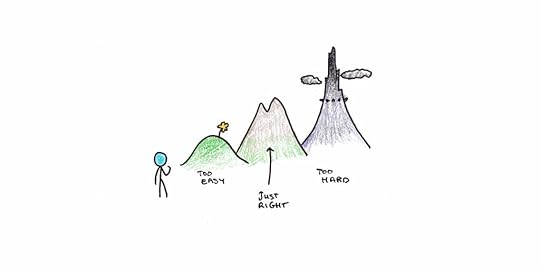

For over four decades, psychologist Edwin Locke has been central in research on goal-setting. His research has three consistent findings:

Setting goals improves performance.Hard goals improve performance more than easy ones.Specific targets work better than simply trying to “do your best.”

Early research on goal-setting found that there is an inverted U-shaped relationship between difficulty and performance.1 This means that easy goals lead to weak efforts, but so do goals that are too hard. The key factor here seems to be that goals need to be challenging, but also believable to be effective. If you don’t think you can actually reach a goal, you won’t.

Thus the best goals to set are those that demand effort from you, but you’re confident you can achieve if you put in the effort.

2. Use the 80% Rule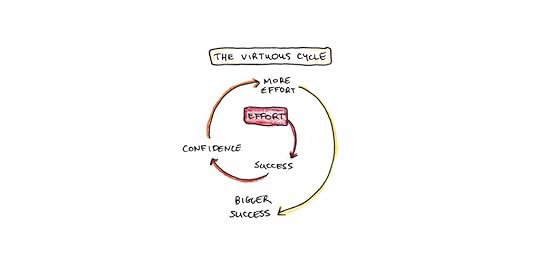

How do we build motivation to pursue our goals? Psychologist Albert Bandura developed the concept of self-efficacy to explain why some people eagerly face challenges while others shrink. If you don’t feel you’ll be successful, why bother?

The danger is that self-efficacy can create either a vicious or a virtuous cycle. If you don’t feel you’ll be successful, you don’t put effort into your goals. This leads to failure and seemingly confirms your inability. The reverse is also true: you can pick successful goals, achieve them and steadily boost your confidence.

One way to build confidence is the 80% rule. Psychologist Barak Rosenshine, in his review of successful teaching, found that this was approximately the success rate students should experience while in school. Too much success, and you’re likely not picking hard enough goals. Too little, and you can fall into the confidence trap.

One way to calibrate this is to set smaller goals (think 30 days) and track your success rate. If you’re under 80%, try setting a more achievable target. If you’re over 80%, try something a little more ambitious.

3. Deadlines Are Poison for Creative Problem-Solving

A significant exception to the power of specific, challenging goals involves creative problem-solving. In tasks that require complex thinking, such as learning, problem-solving or creative work, goal-setting can backfire.

Why is this? It’s because these activities require the full use of your working memory. Working memory is a psychological concept that corresponds roughly to mental bandwidth. It’s been known for several decades that the amount of things we can keep in mind at one time is limited—and often less than we think.

A stressful deadline to come up with a creative solution can hurt. The goal itself occupies so much space in your working memory that you have little left to try out new possible solutions. In these cases, you’re better off in a relaxed state with minimal distractions.

Of course, here we have a conflict. Goal-setting works by marshaling motivation and energy to reach a goal. Without goals, we often fail to put in the effort needed to achieve. However, if we are thinking about the goal while we’re working, we lose that mental bandwidth to develop creative solutions. How do we fix this?

One way is to set goals to work on a creative problem for a chunk of time without interruption or expectation of results. This allows you to focus on the task and gives your mind more space to think of solutions.

4. Visualize Failure

A common suggestion for goal-setting is to visualize success. But visualizing failure might work even better.

Psychologist Peter Gollwitzer suggests a key ingredient to the success of your goals is what he calls implementation intentions. These are when you visualize difficulties that might come up in pursuing your goal and decide in advance how you will handle them.

Many goals get derailed by events that are unexpected but not unimaginable. You get sick two weeks into an exercise program. Your exam gets rescheduled. You were ready to start your business, but the permits are delayed.

Imagining obstacles in advance and deciding your response can make those responses more effective when the time comes. Since your motivation is usually highest when setting the goal, this planning can keep you from abandoning your goal when things get difficult.

5. Keep it to Yourself (At Least to Start)

Should you tell other people about your goals? Surprisingly the answer is sometimes no.

In addition to implementation intentions, Peter Gollwitzer also studied the effects of telling people about the goals you want to achieve. Interestingly, his research found that telling people about your goals can substitute for actually taking action. Why is this?

Gollwitzer explains the results in terms of his theory of symbolic self-completion. According to this theory, we all want to maintain our image in the eyes of others. To do that, we display signals of our self-identity. Announcing our goals can make us feel like we have sent that signal, and our motivation to achieve the actual goal can go down.

This suggests we should focus first on taking action, not talking about it.

6. Break it Down and Make Yourself Accountable

Why do we procrastinate? The common perception is that procrastination is caused by perfectionism. People who need to do everything perfectly waste time getting started.

Except research doesn’t bear this out. In a comprehensive review, psychologist Piers Steel found perfectionism didn’t predict procrastination. What did? Unpleasant tasks and impulsive personalities.

One difficulty with setting goals is that our motivational hardwiring doesn’t cope well with the future. When a deadline is far off, and the immediate work isn’t always fun, we’re likely to slack. This persists until shortly before the deadline when the fear of failure spurs us to action. Unfortunately, as we discussed in point 3, these last-minute efforts aren’t ideal for complex work.

The key is to break down your goals into smaller, daily actions. If you know what needs to be done today, you’re in a much better position to act on it.

It is even better is if you can create a compelling incentive to stick to the daily plan. A powerful tool for overcoming procrastination is precommitment. Telling a friend or spouse that you’ll give them money for each day you miss your plan is a surefire strategy to stay committed.

Less extreme solutions can also include following a “don’t break the chain” strategy. Once you’ve set your daily plan, keep a tally of how many days in a row you’ve followed it. The goal is not to miss a day. If you do, reset your tally and start over.

For goals that don’t break down into simple, daily habits, you can still focus on daily actions. Break the goal into smaller milestones that have short-term deadlines. The closer you can move your goals to the present, the more successfully they will guide your behavior.

7. Set Goals You Want to Achieve (Not Just Those You Feel You Should)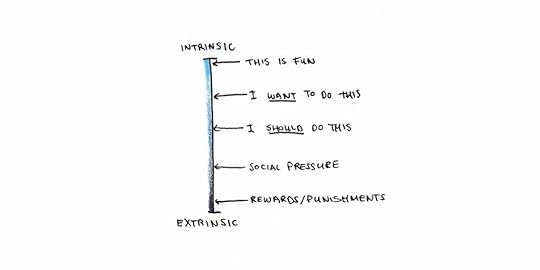

Much of the stress and disillusionment people experience with goals comes from setting ones that aren’t truly their own. When we work on the goals of other people, goals we feel pressure to achieve but don’t actually want, the result is often misery.

Self-determination theory was developed by psychologists Edward Ryan and Richard Deci. They found that external incentives, such as paying someone to complete an otherwise interesting puzzle, could crowd out internal motivation. People would play the puzzle while being paid to, but they would play less when the rewards stopped.

They argue that many of the goals we pursue are only partially our own. We chase them because we feel we should, but they are somewhat “alien” to our deeper selves. Since these goals mainly just fulfill social expectations, they are harder to motivate ourselves toward consistently.

I suspect that the prevalence of these goals is why many have soured on goal-setting altogether. They have too many goals that aren’t truly their own. As a result, they are poorly motivated to achieve them, often fail to put in adequate effort, and experience stress and burnout.

For goal-setting to be life-affirming, the goals pursued have to feel deeply meaningful to you. Getting in touch with what you really want out of life, and separating out the things you merely think you “should” want, is perhaps the most essential part of goal-setting. A good life isn’t measured by the sum of your achievements, but by the meaning you attach to them. Choose wisely.

The post The Science of Achievement: 7 Research-Backed Tips to Set Better Goals appeared first on Scott H Young.

Cognitive Load Theory and its Applications for Learning

Why is learning effortful? Why do we struggle to learn calculus but easily learn our mother tongue? How can we make hard skills easier to learn? Cognitive load theory is a powerful framework from psychology for making sense of these questions.

Cognitive load theory, developed in the 1980s by psychologist John Sweller, has become a dominant paradigm for the design of teaching materials. In this essay, I explain the theory, some of its key predictions, and potential applications for your learning.

Why is Most Learning Hard?

The central concept in cognitive load theory is that we have limited mental bandwidth for dealing with new information, but no such limitations when dealing with previously mastered material.

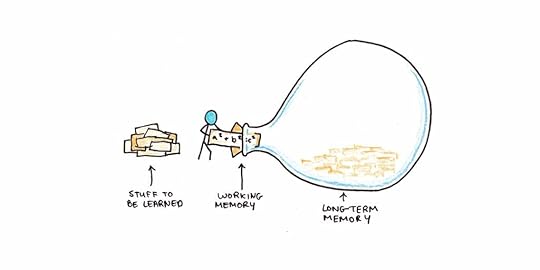
For example, the first time you saw an algebraic expression (e.g., 4 + x = 7), you might have been a bit confused by the “x.” The idea of moving statements probably seemed strange—before that, you just had to calculate what was on the other side of the equals sign.

However, notice what wasn’t confusing: You already knew the numbers. You knew what “+” meant. These things probably didn’t stand out at all since you already understood them. Imagine how much harder it would be to understand algebra if you didn’t already know these things.

This phenomenon explains why we can struggle with challenging classes. Suppose we are missing foundational patterns in long-term memory. In that case, instruction may require us to juggle too many new pieces of information simultaneously. These will slip out of working memory, and we’ll fail to learn.

Why are Some Subjects Learned Effortlessly?

The working memory system is a form of conscious learning. But not all learning is conscious. Psychologists have long marveled at children’s ability to acquire perfect pronunciation in their first language or recognize faces. People socialize into cultures without always being able to articulate those cultures’ rules.

Cognitive load theorists argue that we’re evolutionarily predisposed to learn certain patterns of information. Some of these skills and subjects are acquired without effortful cognitive processing.1

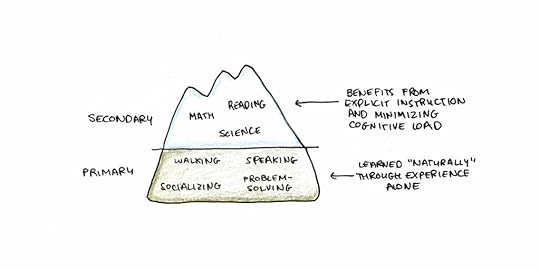
Other skills (such as literacy and numeracy) have not been around long enough for us to have innate learning mechanisms. Instead, we learn these skills by relying on other, innate learning mechanisms (letter recognition seems to co-opt parts of the brain designed for recognizing faces) and more general-purpose learning mechanisms that involve conscious processing.2

This distinction helps explain why we learn some things effortlessly, while other subjects require years of specialized training.

Three Types of Cognitive Load

Cognitive load theory separates three different demands that learning puts on our limited working memory capacity:

Intrinsic load. The combined attention that’s necessary to learn the pattern that will be put into long-term memory.Extraneous load. Unnecessary load distracts from learning the pattern. Obvious distractions that eat up working memory, such as television in the background, make learning harder. But extraneous load also includes mental work needed to learn a subject that isn’t necessary. Poorly organized study materials can increase cognitive load. Examples of this include having to flip between pages to understand a diagram, or making students figure out a pattern that could be taught explicitly.Germane load. Efforts that improve learning outcomes but are not strictly necessary to learn the pattern. Some forms of germane load include self-explanations and retrieval practice, both of which are effortful but increase the ability to recall a pattern later.34

Initially, I found germane load confusing. If excessive cognitive load impedes learning, isn’t the category of “germane” load just a sneaky way of saying sometimes it doesn’t?

Not quite. Working memory has a fixed capacity. If the intrinsic load fills the entire available space, any additional load will be harmful. However, if intrinsic load is not near the maximum, the “spare” capacity can be used for activities that deepen learning.

Consider variable practice, the idea of practicing a skill with an increased range of problems and in different contexts. It’s harder than practice which occurs in only a narrow range of problems. Yet, there’s evidence that variable practice leads to better learning and transfer.5

However, the learning benefit of variable practice only occurs when cognitive load isn’t overwhelmed. If it is, then simpler forms of practice become preferable.6

Key Experiments in Cognitive Load Theory

Over the past few decades, cognitive load theory has amassed a lot of interesting experimental effects with catchy-sounding names. Here are a few:

1. The Worked-Example Effect

Traditionally, math education has focused on having students solve problems to get good at math. Sweller and Cooper pushed back against this idea, showing that studying worked examples (problems, along with detailed solutions) is often more efficient.7

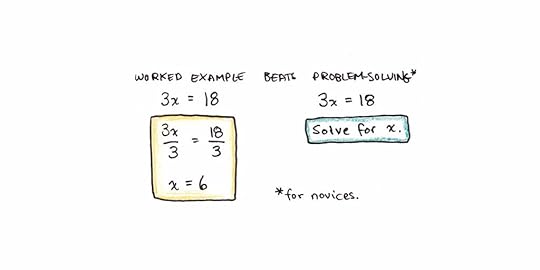
Worked examples have since been shown to be powerful tools in many domains. The rationale is that problem solving is a cognitively demanding activity. This creates a lot of extraneous load, making it harder to abstract what the general solution procedure involves.

Sweller and Cooper, of course, agree that practice is helpful. But they argue in favor of presenting lots of examples first. In their model, practice should start with access to examples so students can emulate the pattern. Finally, practice without the solutions available becomes helpful when the material is learned well enough that retrieval efforts are germane load rather than just too much.

2. The Goal-Free Effect

One reason problem solving is difficult is that it requires you to keep in mind the goal you’re trying to reach, how far you are from the goal, and potential operations to move forward. This creates a lot of cognitive load that makes it harder to identify the solution procedure.

Removing an explicit goal can also reduce cognitive load. For example, a classic trigonometry problem might ask a student to find a particular angle. A “goal-free” way to present this would be to ask students to find as many angles as possible.

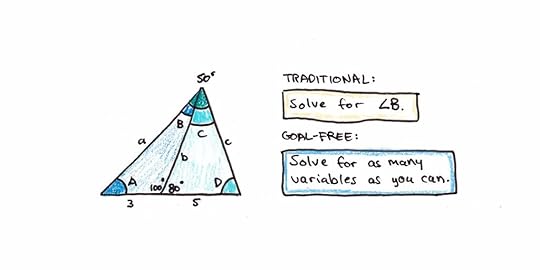
Research shows that early, goal-free problems result in greater learning, consistent with cognitive load theory.8

The downside of goal-free practice, however, is that if there are too many possible actions, most of those explored will be useless. Solving a trigonometry puzzle with several unknowns is helpful. But learning to program by randomly typing in commands is not. Worked examples tend to be a more general tool, since they enable useful patterns to be learned rather than guessed at.

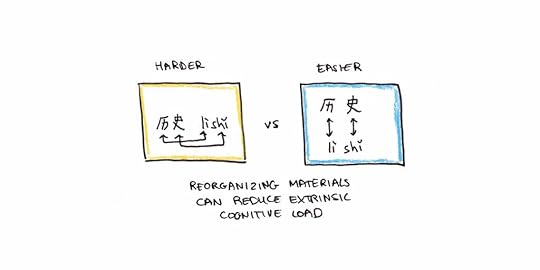
3. The Split-Attention Effect

Cognitive load isn’t just found in problem solving. Badly designed instructional materials can increase cognitive load by requiring learners to move their attention around to understand them.9

Consider these two flashcards for learning Chinese characters. The first creates extra cognitive load since the pairing between sound and character requires more spatial manipulation. Learning is enhanced when instructional materials are organized so that information doesn’t require any manipulation to be understood.

4. The Expertise-Reversal Effect

Cognitive load theory predicts that for novices exposed to information for the first time, worked examples are better than problem solving. But, interestingly, this effect reverses as you gain more experience.10

One explanation for this is in terms of redundancy. If the solution pattern is already stored in your long-term memory, making sense of a worked example doesn’t help much. In this case, it is better to retrieve the answer directly from memory without distracting yourself with the example.

Another explanation is that if the problems are reasonably easy to solve, worked examples may not provoke deep enough processing. Solving a problem yourself is a kind of germane load akin to retrieval practice.

Applying Cognitive Load Theory to Your Studies

Cognitive load theory’s principal applications are in instructional design. How should a subject be taught so that students will efficiently master the patterns of knowledge it contains? Cognitive load theory favors direct instruction, quick feedback and plenty of practice.

However, as learners, we’re often just given instructional materials. What can we do to optimize cognitive load, given that perfect explanations and studying resources aren’t always available?

Here are a few suggestions:

1. Study examples before solving problems.

While some amount of “figuring things out” is often the only path available, this can make it harder to grasp the key concepts. There are a few tools you can apply, as a learner, to make this easier:

Look for examples online. Khan Academy and many other websites offer detailed instructions and worked examples for common problems.Look for problem sets with solutions. This was a big part of my MIT Challenge. Copious problem sets with solutions let you shift between studying the steps of a worked solution and practicing it yourself. This approach tends to beat instructions that only talk about problem solving at a general level (and omit the specifics of a worked example). It also allows you to shift to solving problems yourself once you’ve gotten a good grasp of the material.Self-explain your homework when given feedback. In a traditional class, solutions often aren’t provided until long after the homework assignment. In this case, after you get the solutions, spend the time to thoroughly explain to yourself the solution to problems you found difficult. Self-explanations are a germane load that ensures your homework feedback is put to good use.

This approach applies to non-technical subjects as well. When learning to paint, I made heavy use of video tutorials where I worked on the same painting as the instructor. I’d usually watch the video through once, then work alongside the instructor on a second pass.

2. If a class confuses you, slow it down early.

In my experience, the Feynman Technique mainly works by slowing things down. A concept can be confusing in a lecture because critical assumptions aren’t made explicit or intervening steps are skipped. Walking through the explanation yourself lets you figure out exactly where you get lost.

A difficult class is one where cognitive load is near your maximum. Sometimes it will go too far, and you’ll get lost. Catching these moments early and fixing them is a big part of staying on top of your studies. Since omitted knowledge is often reused in later parts of the class, failing to understand something important in an early lecture can mean the rest of the class time is wasted.

3. Build your prerequisite knowledge and procedural fluency.

Cognitive load theory is most important in domains where there is great element interactivity. This means that many different pieces of information all need to be in place before you can understand the problem. In contrast, a subject might have extensive difficulty. In this case, there may be a large body of information to learn, but you rarely need all of it at once.

Math and science tend to have high element interactivity, which is why mastery of them is seen as a sign of intelligence. Working memory is associated with intelligence, and those with slightly more working memory can handle slightly greater element interactivity. While this creates only a modest advantage in the short term, greater ease in learning basic concepts can accumulate into a considerable advantage in the long run.

If you’re struggling in a subject with high element interactivity, the key is to go back and invest in more practice in the underlying skills. Doing this will make you more fluent in the component knowledge, which frees up more working memory for handling the new topics.

My Changing Views on Cognitive Load

I’ll confess, I didn’t fully appreciate cognitive load theory when I first encountered it. I tended to equate “problem solving” with “practice.” Since practice is essential for learning, I reasoned that problem solving must be equally important. Real life involves a lot of problem solving, so why shouldn’t you practice it?

There seem to be two good answers to my misconception:

Problem solving isn’t a skill. The way we get good at solving problems is by having (a) knowledge that assists in solving the problem and (b) automatic procedural components that help in solving problems. There are probably no general problem solving methods that work for every domain. Heuristics for problem solving within a domain might exist. Still, the significance of these is overwhelmed by the power of having tons of learned patterns in memory. This explains why transfer is elusive and why expertise tends to be specific.Practice improves fluency, but it’s most efficient to have the right method first. It is critical for complex skills with many interacting parts. Figuring out what works through trial and error is inefficient. Worked examples, clear instructions, and background knowledge all help to put practice on the right tracks.

When I discussed these revelations with a friend, he asked how they might have changed my previous learning projects. I can think of a few places where I made mistakes:

During my portrait drawing challenge, I initially focused on getting lots of practice with feedback. However, taking the class with Vitruvian Studios made the most significant difference. A good method can save countless hours of practice.Cognitive load theory helps me make sense of the optimal time to start immersion when learning a language. For Vat and I, the ~50 hours we spent on Spanish was enough to get going relatively smoothly. Yet even 100 hours in Chinese was still a bit of a grind for me when we first arrived. For Korean, we ended up doing most of the preparatory work in Seoul, which was a somewhat wasted opportunity. Cognitive load theory helps explain how the design choices Vat and I made on the trip made some parts more successful than others. (For instance, Google Translate was a great way to alleviate cognitive load in speaking situations that otherwise would have been above our level.)The cognitive load was too high in my quantum mechanics project. Part of this was the several-year gap I had since using calculus and differential equations. The components weren’t as fresh, so I was relearning a little too much. But a bigger part was that I didn’t have as many problem sets with solutions as I would have liked. If I had more, I could have used the first batch as worked examples rather than needing to use them sparingly. In the future, I’d probably do some warm-up to refresh my prerequisite skills and seek out a textbook with tons of sample problems and solutions so I could study with a tighter feedback loop.

Even after fifteen years of obsessing about the topic, I’m always working to refine my learning process. As always, I’ll continue to share what I find with you.

The post Cognitive Load Theory and its Applications for Learning appeared first on Scott H Young.

The Best Essays of 2021

As the year ends, I thought I’d revisit some of my favorite entries from the past twelve months:

The Productivity Frontier: Can You Get More Done Without Making Sacrifices? – How much more productivity can you squeeze out of your day? Is such a squeeze sustainable? Productivity enthusiasts like me often talk about systems to maximize the amount you can do. But sometimes, it’s more helpful to look at trade-offs and make decisions about what to prioritize.Is Life Better When You’re Busy? – Research suggests we prefer activity to idleness, sometimes to the point that we busy ourselves unnecessarily. Is there a sweet spot for busyness that keeps up engaged but not overwhelmed?Is Modernity a Myth? – My review/explainer of Bruno Latour’s fascinating (and confusing) book We Have Never Been Modern. While postmodern philosophy always walks a line between profundity and nonsense, Latour’s writing kept me thinking for weeks—a sign of a good book!Digging the Well – We spend years digging deep wells of expertise to sustain our professional lives. But what do you do when the water runs dry?How I Do Research – Some thoughts on the research process from a non-expert researcher. How do you make sense of topics you’re unfamiliar with? How do you reach sound conclusions on issues that matter? Research is a lot of work, but it seems to be a skill worth learning.My 10 Favorite Free Online Courses – This list proved to be (by far) my most popular work of 2021. If you’re interested in learning something new in 2022, here’s a great place to start.The Craft is the End – Why do we strive to be successful? What if we never get the respect we feel we’re due? Some meditations on C. S. Lewis’s famous speech, “The Inner Ring,” and the goal of finding work we can be proud of.

I’ll be back next week with new writing. Happy holidays!

The post The Best Essays of 2021 appeared first on Scott H Young.

Digging into How We Teach and Learn: 7 Books That Have Challenged and Shaped My Thinking

In my quest to understand the nuts-and-bolts process of how we learn complex, valuable skills, I’ve read quite a few books on learning, teaching and skill acquisition.

This batch of books challenged my thinking and changed my mind on quite a few things. I read these books to further investigate learning by doing and the problem of transfer. Transfer of learning (when you learn one thing and apply it to something else) has been a notorious problem in education, something that piqued my interest when writing Ultralearning.

Below are seven books that influenced me the most.

1. The Power of Explicit Teaching and Direct Instruction by Greg Ashman

Ashman is a fierce critic of giving students complex, open-ended problems as a tool for learning. Instead, he argues, the material needs to be broken down into digestible chunks. Everything we want students to learn needs to be spelled out explicitly, much more explicitly than many teachers realize.

Ashman draws on two bodies of evidence to support his views. The first is the original research on Direct Instruction. These studies were among the most extensive educational experiments in history. They showed that Direct Instruction beat many alternatives that gave less guidance.

The second body of evidence Ashman draws on is from Cognitive Load Theory (CLT). CLT argues that working memory is limited, but patterns stored in long-term memory aren’t. Therefore, the goal of learning is to move patterns from working memory into long-term memory. Give too much information at once, and students fail to learn.

I quite enjoyed this book, even as it forced me to make serious revisions to my previous beliefs.

2. Theory of Instruction by Siegfried Engelmann and Douglas Carnine

After Ashman’s introduction, I decided to go to the source. Siegfried Engelmann and colleagues developed Direct Instruction in the 1960s with the specific aim of teaching disadvantaged students. Theory of Instruction is Engelmann’s magnum opus, fully articulating how the theory could potentially teach any skill.

How does it work? The basic idea of Direct Instruction is to reduce the material down to a minimal set of concepts, procedures, and actions and then to build those up into increasingly complex performances.

Describing the entire system is impossible in the few paragraphs I have here. But the central ideas in the system are:

The aim of teaching is flawless communication. Instead of assuming failure lies with the student, assume the problem is one of communication. Most teaching is incomplete, and thus leads to gaps in understanding by students. While bright and knowledgeable students can easily fill those gaps, those who can’t are left behind.Students learn through examples. Both examples of a quality and similar non-examples are essential because otherwise you can’t know the full range of application of a new idea.Students can learn skills by breaking them down into parts.Short bursts of instruction need to be accompanied by immediate practice and feedback.

The advantage of Direct Instruction is that, given a well-tested curriculum, it can be a superior method for learning complex skills like reading or arithmetic. The disadvantage is that designing, executing and testing such a curriculum isn’t easy.

Many teachers’ hostility to Direct Instruction may be the same as craft autoworkers’ hostility to early assembly line plants. Once a craft executed only by skilled mechanics, modern cars are made using assembly-line production. By seeming to reduce the role of the teacher to following a lesson plan in lockstep, the craft elements that draw people to the profession might be lost.

3. Constructivist Education: Success or Failure? Edited by Sigmund Tobias and Thomas Duffy

Constructivists argue that the student must create knowledge for it to be meaningful. Explicit instruction advocates argue that discovery learning, championed by constructivists, is inefficient and wasteful. If something is important for students to know, why not just teach it to them directly?

This book was compiled in response to a 2006 paper by Sweller, Kirschner and Clark. Their article argued that constructivist approaches to education fail because they do not fit into what we know about how human memory works. Prominent researchers from both sides of the debate contributed essays sharing their perspectives, agreement and disagreement between the schools of thought.

The major conclusion I gathered from this book is that both sides agree that guidance is helpful for learning. However, explicit instruction advocates prefer giving students everything needed to solve a problem up front. Constructivists suggest that letting students come up with solutions themselves leads to deeper learning. This latter belief is intuitively appealing, but there is good evidence against it.

In the end, I felt like the advocates of explicit instruction had the upper hand in terms of evidence. While good constructivist education might be achievable by excellent teachers with bright students, Direct Instruction seems a more reasonable approach for wide-scale public education.

4. Learning and Memory by John Anderson

Anderson’s textbook, Learning and Memory, was fascinating as a discussion of experimental evidence for learning and its history within psychology. Anderson began in the behaviorist learning tradition and shifted into cognitive research on memory. Today, he’s most famous for his ambitious ACT-R theory, which attempts to provide a model for human cognition.

One tidbit I appreciated was his explanation of the difference between conditioning and learning curves. In a conditioning experiment, an animal is given rewards to shape behavior. But, given the non-human participants, no instructions are provided. In a learning experiment, a human is usually given explicit instructions, and their performance is monitored. Conditioning curves are s-shaped showing that they are slow to improve in the beginning, and learning curves shoot up immediately.

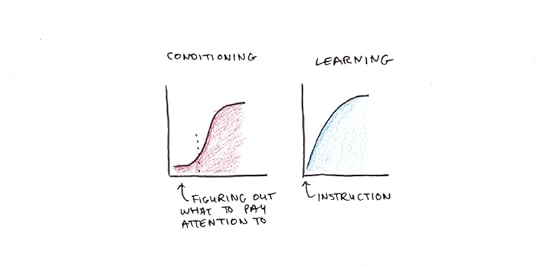
The difference seems to be that the animal has to “figure out” which aspects of its behavior are being rewarded in a conditioning experiment. In contrast, humans can be told where to pay attention so learning begins almost immediately. This subtle effect shows some of the influence of instruction on learning.

5. Ten Steps to Complex Learning by Jeroen van Merrienboer and Paul Kirschner

One major criticism of Direct Instruction is that stripping knowledge away from its useful context can make it difficult to understand the big picture. This is part of the constructivist critique of traditional schooling. While the solutions proposed have their flaws, the issues of meaningless learning are valid.

Ten Steps to Complex Learning is an attempt at a different solution to the same problem: how do you teach complex skills without overwhelming students?

The basic strategy outlined is to organize the curriculum based on real-world task categories. Tasks proceed from easiest to hardest. Within each category, instructors provide structured guidance that lessens over time until the student can perform the full range of tasks without problems.

The authors recommend students learn essential background knowledge ahead of time and that teachers give instructions alongside practice. The whole process is designed to minimize cognitive load during learning. Drills on procedural components are only used for a minority of fixed routines. In addition, students are given help with developing self-directed learning skills. The hope is that when students leave the program, they are equipped with tools to continue their training independently.

6. Learning and Instruction by Richard Mayer

I found this book’s discussion of the best way to teach basic skills such as reading, comprehension, and math, fascinating.

Mayer argues that children who struggle with aspects of a complex skill can improve with instruction and practice targeted on the components of the skill where they are weak. Examples include helping students recognize the sound components inside spoken words through rhyming exercises, decoding the sounds of written words through phonics training and helping students construct diagrams to assist with word problems in math. Skills are complicated, and a failure to learn is usually a breakdown of one of the essential components needed for performance.

7. The Mind is Flat by Nick Chater

Chater presents a radical view of the mind: The mind is what you’re currently experiencing. There are no hidden, unconscious depths, no beliefs and motives. Instead, he argues, we infer these things the same way we would the beliefs and motives of fictional characters—from the context cues surrounding them.

In this model, our minds are constantly engaged in a “grand illusion” that gives us the impression there is more going on than is really there. We imagine an entire visual scene presented before us, but in reality, we only have a tiny cone of detailed perception. The illusion of broader perception is sustained because we can flick our eyes and look at something as soon as we want to.

This grand illusion goes beyond visual perception. Chater argues our internal states, moods, and beliefs are assembled as we think about them. Mentality, then, is a constant process of inference, not just about the external world but about the details of our own lives.

On My Reading List

Some books I have lined up to read next include:

How Learning Happens by Paul Kirschner and Carl HenrickRules of the Mind by John AndersonApprentice to Genius by Robert KanigelEducation and Mind in the Knowledge Age by Carl BeretierGenius and the Mind Edited by Andrew Steptoe

As I read more, I’ll share my more interesting findings with you!

The post Digging into How We Teach and Learn: 7 Books That Have Challenged and Shaped My Thinking appeared first on Scott H Young.

How Much Do You Need to Know Before Getting Started?

Say you need to learn a complicated skill: physics, French or computer programming. How much time should you spend building your background knowledge before you start practicing the actual skill?

Consider machine learning. One way to learn this field would be to master first the underlying math. Then, when you encountered the programming commands for certain mathematical functions, you’d know what they are doing behind the scenes.

Another way to approach this field would be to make machine learning models for things that interest you. You could get reasonably far with this without knowing calculus and linear algebra. Perhaps then the math is best saved for later?

The question of how much prerequisite work is necessary before attempting the real task occurs in many spaces. How much time should you spend in school before doing real-world work? How long should you study a language before trying to speak it? How many books should you read before starting a business?

Let’s look at some of the cognitive science for some guidance.

What are the Prerequisites to Learning a Skill?

Obviously, if specific concepts are used to teach a subject, you need to learn those concepts first.

When I took MIT’s economics classes, they were taught using calculus. Not knowing calculus would have made solving the problems for the exam impossible. It also would have made many of the conceptual explanations harder to grok, since they were framed in terms of calculus.

However, this answer isn’t too satisfying because subjects can be taught at different levels of depth. For instance, when I took economics in my alma mater, they didn’t use calculus.

I feel like I understood economics better the MIT way. But that’s a bit of a silly argument because, of course, it’s easier to understand something when you have a deeper presentation. The question is whether it makes sense to ask everyone who wants to learn economics to first study calculus.

Cognitive Skill Acquisition

At a basic level, we can contrast two ways of learning. One way is to memorize, by rote, the answer to every possible question in a domain. The other way is to learn a process for generating solutions in the domain.

Consider basic addition. The memorizing approach would involve memorizing all pairs of one-digit addition facts by heart (e.g., 7+4=11, 3+6=9, etc.). The procedural approach might involve counting: Pick the bigger number, then count up by one the number of times equal to the lower number (e.g., 7 + 4 = 8… 9… 10… 11!).

Interestingly, children seem to do exactly this when learning arithmetic.1 They begin with a procedure, like counting. As they gain experience, they memorize more and more of the exact answers. Eventually, they are able to solve most arithmetic problems through recall alone, and the procedure of counting fades away.

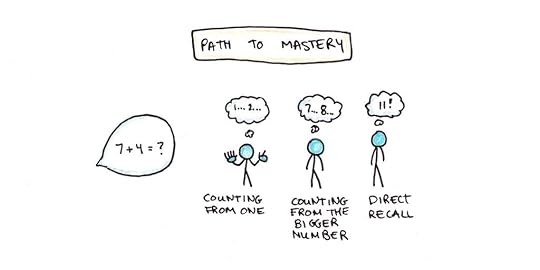
Four things are worth noting here:

Eventually, many answers are memorized. This results in fast, reliable access and helps us perform complicated skills smoothly. You won’t perform well if you need to reason from first principles in everyday situations.The procedure of counting is more compact than an array of memorized facts. Thus the method is learned first, with fluently recalled answers coming only after much more experience.The counting procedure can act as a backup. Say you haven’t memorized 24 + 3. The counting procedure is slow, but it can help you answer the question (25… 26… 27!). If you have memorized other facts, you may use a different ad-hoc procedure (4+3 = 7, add 20).2The choice to use memorization or a procedure to find an answer depends on the effort needed to perform the procedure, the reliability of the procedure, and incentives surrounding accuracy. Children tend to choose low-effort tools like guessing and retrieval unless they are required to use a more effortful procedure.

When performing skills, we use a variety of methods, from following a procedure to retrieving an answer from memory. With increased practice, the memory component becomes dominant for routine situations. Even when we can’t get the exact solution from memory, we may find parts of the answer which we can use to solve the problem faster.

This suggests that digging deeper has two benefits:

It can provide a strategy to obtain the correct answer when memory fails. This backup is essential in the early phases of learning when many patterns haven’t been stored yet.It can assist in non-routine situations where no answer is known.

However, this analysis also shows a limit to background knowledge. Since fluent performance of a skill is mostly driven by recalling direct experiences and examples, deeper and deeper knowledge mostly helps in cases where direct experience is missing or insufficient. This becomes more and more important as you reach increasing levels of expertise, but it may not be helpful for routine performance.

Should You Dig Deep or Dive Right In?

The evidence from skill acquisition paints a mixed picture. On the one hand, methods that directly assist with learning a domain are necessary prerequisites. Even if a brute-force approach might work, good methods are more reliable than trial-and-error.

On the other hand, routine performance is largely handled by drawing on direct experience—not working from first principles. Thus, if the principles don’t actually lay out the actions needed for routine situations, then they are mainly helpful in non-routine cases. These principles will probably only be relevant as your experience within a field grows.

What are your experiences? Do you prefer to step back and dig deep before trying to practice a skill? Or do you prefer diving in and practicing directly? I’m interested to hear your thoughts.

The post How Much Do You Need to Know Before Getting Started? appeared first on Scott H Young.