Holly Tucker's Blog, page 44

The Simply Complex Cipher: Chaocipher

By Hamza Patel (Guest Contributor)

“She was an open book to me, All of it in Code,” Jocko Benolt, Flickr (CC)

Imagine a cipher machine so simple that it could fit inside a cigar box. Now imagine that this same cipher was so complex that it remained unsolved for a half century. In fact, it could only be solved after the family of the inventor revealed the logistics of the simple machine. John F. Byrne accomplished this exact feat with the Chaocipher system he invented in 1918.

John Byrne was born in Ireland in 1880, and he was an extremely close friend of the famous writer, James Joyce. He moved to New York in 1910, and took up a position as a writer. In the year of 1918, Chaocipher was nothing more than an idea in John Byrne’s head. But from 1920 onward, chaocipher would become Byrne’s sole passion (Rubin 2011).

Byrne tried multiple times in the years between 1918 and 1953 to bring his “indecipherable” cipher to the attention of the United States government. He tried approaching people in the U.S. cryptanalyst department and even the Navy, but he was turned down multiple times. The main reason for this rejection was that Byrne was not a cryptanalyst, so he did not understand certain implications when asked to disclose information about specific bits of the cipher, including multiple copies of plaintext and ciphertext. He refused to send the full details of his chaocipher system with several plaintexts and ciphertexts, replying that his system was truly indecipherable (Rubin 2011).

It was not until Byrne published his autobiography, Silent Years, in 1953 that the Chaocipher was finally available to the public. One of the main reasons John published his novel was to disclose the information about this cipher. He included examples of enciphered texts such as the Declaration of Independence and the Gettysburg Address to give the reader examples of ciphertext and plaintext pairs (Rubin 2011). The real challenge presented in the novel was to figure out the chaocipher system itself and decipher the challenge ciphertext.

There were many failed attempts at solving the Chaocipher from the time of the autobiography to the time of its disclosure. David Kahn incorrectly assumed that the cipher was an autokey cipher, which is a cipher that includes parts of the plaintext in the key itself. This means that the plaintext being enciphered creates parts of the key as it is being enciphered.

In the latter half of the 1970s, members of the American Cryptogram Association unsuccesfully tried to contact Byrne’s son in the hopes of convincing him to disclose information regarding the cipher. Byrne’s son did not want the machine his father worked so hard on to be revealed so easily to the general public. He did, however, reveal several hints as to how the chaocipher system worked several years later. But people were still stumped.

As late as 2009, cryptanalysts were still trying to figure out the workings of the chaocipher system. In 2010, the chaocipher was finally revealed to Rubin by Patricia Byrnes, John Byrne’s son’s widow. Then on June 2, Rubin published the first full disclosure of the chaocipher system, revealing its inner mechanism (Rubin 2011).

The Inner Mechanism of the Chaocipher

The basic model of Byrne’s machine consists of two wheels, each with the entire alphabet on removable tabs around its periphery (Cowan 2010). The alphabets are arranged in a clockwise manner on the right disk and an anticlockwise manner on the left one. The right disk consists of the plaintext letters while the left disk consists of the ciphertext letters.

Let’s say we are trying to encipher the letter “L.” We will rotate the right wheel so that this letter is at the top of the wheel. Since the wheels are connected like gears, turning the right wheel also turns the left. For simplicity, let’s assume that that turning the left wheel also results in the letter “L” and that the wheels are in alphabetical order. So in this case, the letter “L” would be enciphered as the letter “L.”

Now the alphabets on both disks must be permuted in order to encipher the next letter. For the left disk, we must extract the letter to the left of the letter that was just used to encipher the plaintext letter. Then shift all the letters to the left of the extracted letter up to the bottom letter of the disk to the right to fill up the space of the extracted letter. Finally, insert the extracted letter into the space that is now empty at the bottom of the disk (Rubin 2010).

In our example with the letter “L,” the letter “M” would be extracted, and all of the letters up to the letter “Y” will be moved to the right in order to fill the space that the extracted “M” left. Finally, the letter “M” will be placed at the bottom position of the disk in the position that “Y” had previously. This process is repeated for every new encipherment of every new letter. The sequence of letters would go from this:

To this:

Next, we must permute the right disk. The permutation of the right disk is slightly different from that of the left disk. After the first letter is enciphered, the disk is rotated by itself one more position to the left. Now, the letter that is two letters to the right of the letter that is currently at the top is extracted. Then, all of the letters to the right of that letter up to the bottom letter of the circular disk are shifted to the left in order to cover up the space that is left by the extracted letter (Rubin 2010).

In our example with the letter “L,” the disk will first be rotated to the left so that “M” is at the top. Then the letter two letters to the left of “M,” “O,” will be extracted. Then every letter up to the letter “Z,” which is at the bottom of the disk, will be shifted to the left. Finally “O” will be placed at the bottom of the disk. This permutation process is repeated with every new encipherment. This repetition causes the entire alphabet on both wheels to quickly permute into an entirely different sequence of letters. The sequence of letters would go from this:

To this:

Once the entire process is revealed, the Chaocipher becomes very simple (Rubin 2010). How then did it remain unsolved for so long? There are several reasons. No one knew how the cipher was constructed, so no one conceived of the way John Byrne used the alphabet disks. The only information given was the ciphertext and the plaintext. But now, how does one go about deciphering a message encrypted by this Chaocipher process? Deciphering the Chaocipher is similar to enciphering. The only difference is that the cipherer must locate the ciphertext on the left disk and find the corresponding letter on the right disk. Permuting the disks is the exact same as it is for the process of enciphering (Rubin 2011). It is a forward and reverse process in and of itself.

The cipher violates Kerkchoff’s principle, the principle that states that the strength of the system is determined by how strong the cipher is assuming that the enemy has full information as to how the cipher was constructed. Once the process was revealed, cracking the cipher becomes very simple.

Yet, this two wheel permutation algorithm did remain elusive from even the nation’s best cryptanalysts for over fifty years. What makes this cipher impressive is that Byrne never had any real formal training in cryptography. Even more impressive, the chaocipher algorithm was never actually found; it was only revealed. The Chaocipher truly is one of the simplest yet most complex ciphers developed in modern cryptography.

This post is part of a series of essays on the history of cryptography produced by students at Vanderbilt University in honor of the release of The Imitation Game, a major motion picture about the life of British codebreaker and mathematician Alan Turing. The students wrote these essays for an assignment in a first-year writing seminar taught by mathematics instructor Derek Bruff.  For more information on the cryptography seminar, see the course blog.  And for more information on The Imitation Game, which opens in the US on November 28, 2014, see the film’s website.

Sources:

Cowan, Michael J. (2010). Chaocipher: Solving Exhibits 1 and 4. Retrieved from http://www.cryptoden.com/articles/Cha....

Rubin, M. (2010). Chaocipher Revealed: The Algorithm.

Rubin, M. (2011). John F. Byrne’s Chaocipher Revealed: An Historical and Technical Appraisal. Cryptologia, 35(4), 328-379.

Let’s Play Fair: A Deceptively Simple Cipher

By Nathan Dumessa (Guest Contributor)

“Good Bye.” by Zarko Drincic via Flickr CC.

What is the best way to keep your secret messages safe? Using a cipher that is deceptively simple. This is what makes the Playfair cipher stand out among the other ciphers.

Charles Wheatstone may be more famous for his contributions to the invention of the telegraph, but what some may not know is that he invented the Playfair cipher, which he named after his friend, Lyon Playfair. Wheatstone was also an important figure in the study of vision. He made a revolutionary contribution with his invention of the stereoscope in 1838 (Banerjee, 2014). This was one of his greatest inventions that led to his popularity. In addition, his work on the telegraph may have led to the creation of the Playfair cipher. After all, the invention of the telegraph was a game-changer in the world of cryptography.

One of the most famous uses of the Playfair Cipher involved John F. Kennedy during World War II (Lyons, n.d.). He was able to send a message encrypted using this cipher when his PT-109 sank in the Solomon Islands and managed to get his crew and himself rescued.

What I really admire about this cipher is how simple it can seem, but is actually difficult to decipher. The structure of the Playfair cipher is a 5×5 grid of the English alphabet. This will of course exclude a letter, but in this cipher, the letters I and J are combined to represent one letter. Similar to the Keyword Cipher, the Playfair cipher also uses a keyword. The rules for the keyword apply here as well with the addition of one new rule: If any letter is repeated in the key, it is eliminated, the entire grid has to contain all of the letters except for J since it is represented by the letter I, and finally the key cannot contain the letters J and I.

The next step to setting up this cipher is to split up your message into two-letter pairs called digraphs. When doing this, you have to disregard all punctuation and write out any numbers that may be included. Now there are a few restrictions that apply here: Any double letters are separated by the letter X, and if you have an odd number of letters in your message, you add an extra X at the end to make it even, for example, the word BELL would be written as BE LX LX. Now the only thing left is to encrypt the message. So for this example our sentence will be HE RANG THE BELL AT SEVEN PM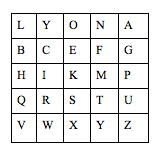

The sentence would then be broken apart into: HERANGTHEBELLATSEVENPM

HE RA NG TH EB EL LA TS EV EN PM

Note that it was not necessary to put an X between the two L’s in the word BELL because they were in two separate digraphs.

The encryption process has a specific algorithm. For our example, we will use the keyword LYON and set up a grid first.

Now to encrypt our message, we will look at each pair of letters at a time.

HE RA NG TH EB EL LA TS EV EN PM

The way you encrypt each pair is by looking at their locations in the grid, so HE forms a 2×3 rectangle. You start by looking at the H and following it to the E column and you get the letter K. Then you follow the E left to the H column and you get the letter B. So the first pair will be encrypted to KB.

If two letters are located in the same row, you would shift one position to the right. For example, if you are trying to encrypt the letters IM, it would be translated to KP. If the letters are in the same row and in the first or last columns for example LA, you would translate it to YL. Similarly, if two letters are in the same column, you would shift down one position so the letters AP for example, would be encrypted to GU, and following the same pattern, CW would be translated to IY.

So our message would be encrypted to:

HE RA NG TH EB EL LA TS EV EN PM

KB UY AF QM FC BO YL UT BX FO HP

Or: KBUYAFQMFCBOYLUTBXFOHP

“Time Is Running out.. Explored.” By richardbrunsveld.nl. via Flickr CC..

The main weakness of the Playfair cipher is the fact that the sender would have to inform the recipient of the keyword. If an enemy were to intercept this information, the message would be decrypted in a very short amount of time. However, without information on the key, cracking this cipher would prove to be a daunting task.

In attempting to cryptanalyze a message like this, one would first need to figure out whether or not it is a Playfair cipher. The important characteristics are: an even number of letters, no double letters, and if it’s a long message, a frequency analysis that shows no more than 25 letters. Once that is done, most of the approach involves a trial and error method. Contextual evidence would help because it would provide some plausible guesses. Because the cipher is digraphic, substituting a pair of letters at a time, frequency analysis would not be an efficient method to decipher it. Therefore, a cryptanalyst would have to use a different approach to crack this cipher. One thing to consider is that in this cipher, reversed plaintext digraphs correspond to reversed cipher text digraphs, so that would help pick out a few letters.

The Playfair cipher was actually used in World War II by the German army, but instead of using the regular cipher, they used a double Playfair which eliminated the weaknesses in the cipher (Christensen, 2006). In the double Playfair, the first letter of the digraph would be in one grid and the second would be in the other. Therefore, reversed plaintext digraphs would not actually correspond to reversed cipher text digraphs. In addition, double letters could be present in the cipher text which can give a false pattern to a cryptanalyst.

The Playfair cipher is one that is very simple to utilize but time consuming and difficult to decipher. The main weakness is how easy it is to crack it if someone knows the keyword. Otherwise, it is one of the best ciphers to securely encrypt a message as long as your intended recipient knows the key. It is important to note that the keyword is vital. The security of the message depends on the mutual understanding of the key between the sender and recipient and as little written evidence of it as possible.

I will leave you with this:

TAZSQVRMIPPBLMDQDYRIRFEPDATAQLMCRCPQAFTAFAVAMIIDLMALEOIMERVTHFSVKZ

This post is part of a series of essays on the history of cryptography produced by students at Vanderbilt University in honor of the release of The Imitation Game, a major motion picture about the life of British codebreaker and mathematician Alan Turing. The students wrote these essays for an assignment in a first-year writing seminar taught by mathematics instructor Derek Bruff.  For more information on the cryptography seminar, see the course blog.  And for more information on The Imitation Game, which opens in the US on November 28, 2014, see the film’s website.

Sources:

Akins, T. Playfair Cipher. (n.d.). Retrieved October 15, 2014. http://rumkin.com/tools/cipher/playfair.php.

Banerjee, J. (2014, August 15). Charles Wheatstone (1802-1875). Retrieved October 15, 2014. http://www.victorianweb.org/technology/inventors/wheatstone.html

Christensen, C. (2006, January 1). Playfair Cipher. Retrieved October 15, 2014. http://www.nku.edu/~christensen/section%2019%20playfair%20cipher.pdf

Lyons, J. Playfair Cipher. (n.d.). Retrieved October 15, 2014. http://practicalcryptography.com/ciphers/playfair-cipher/

Let’s Play Fair

By Nathan Dumessa (Guest Contributor)

“Good Bye.” by Zarko Drincic via Flickr CC.

What is the best way to keep your secret messages safe? Using a cipher that is deceptively simple. This is what makes the Playfair cipher stand out among the other ciphers.

Charles Wheatstone may be more famous for his contributions to the invention of the telegraph, but what some may not know is that he invented the Playfair cipher, which he named after his friend, Lyon Playfair. Wheatstone was also an important figure in the study of vision. He made a revolutionary contribution with his invention of the stereoscope in 1838. This was one of his greatest inventions that led to his popularity. In addition, his work on the telegraph may have led to the creation of the Playfair cipher. After all, the invention of the telegraph was a game-changer in the world of cryptography.

One of the most famous uses of the Playfair Cipher involved John F. Kennedy during World War II. He was able to send a message encrypted using this cipher when his PT-109 sank in the Solomon Islands and managed to get his crew and himself rescued.

What I really admire about this cipher is how simple it can seem, but is actually difficult to decipher. The structure of the Playfair cipher is a 5×5 grid of the English alphabet. This will of course exclude a letter, but in this cipher, the letters I and J are combined to represent one letter. Similar to the Keyword Cipher, the Playfair cipher also uses a keyword. The rules for the keyword apply here as well with the addition of one new rule: If any letter is repeated in the key, it is eliminated, the entire grid has to contain all of the letters except for J since it is represented by the letter I, and finally the key cannot contain the letters J and I.

The next step to setting up this cipher is to split up your message into two-letter pairs called digraphs. When doing this, you have to disregard all punctuation and write out any numbers that may be included. Now there are a few restrictions that apply here: Any double letters are separated by the letter X, and if you have an odd number of letters in your message, you add an extra X at the end to make it even, for example, the word BELL would be written as BE LX LX. Now the only thing left is to encrypt the message. So for this example our sentence will be HE RANG THE BELL AT SEVEN PM

The sentence would then be broken apart into: HERANGTHEBELLATSEVENPM

HE RA NG TH EB EL LA TS EV EN PM

Note that it was not necessary to put an X between the two L’s in the word BELL because they were in two separate digraphs.

The encryption process has a specific algorithm. For our example, we will use the keyword LYON and set up a grid first.

Now to encrypt our message, we will look at each pair of letters at a time.

HE RA NG TH EB EL LA TS EV EN PM

The way you encrypt each pair is by looking at their locations in the grid, so HE forms a 2×3 rectangle. You start by looking at the H and following it to the E column and you get the letter K. Then you follow the E left to the H column and you get the letter B. So the first pair will be encrypted to KB.

If two letters are located in the same row, you would shift one position to the right. For example, if you are trying to encrypt the letters IM, it would be translated to KP. If the letters are in the same row and in the first or last columns for example LA, you would translate it to YL. Similarly, if two letters are in the same column, you would shift down one position so the letters AP for example, would be encrypted to GU, and following the same pattern, CW would be translated to IY.

So our message would be encrypted to:

HE RA NG TH EB EL LA TS EV EN PM

KB UY AF QM FC BO YL UT BX FO HP

Or: KBUYAFQMFCBOYLUTBXFOHP

“Time Is Running out.. Explored.” By richardbrunsveld.nl. via Flickr CC..

The main weakness of the Playfair cipher is the fact that the sender would have to inform the recipient of the keyword. If an enemy were to intercept this information, the message would be decrypted in a very short amount of time. However, without information on the key, cracking this cipher would prove to be a daunting task.

In attempting to cryptanalyze a message like this, one would first need to figure out whether or not it is a Playfair cipher. The important characteristics are: an even number of letters, no double letters, and if it’s a long message, a frequency analysis that shows no more than 25 letters. Once that is done, most of the approach involves a trial and error method. Contextual evidence would help because it would provide some plausible guesses. Because the cipher is digraphic, substituting a pair of letters at a time, frequency analysis would not be an efficient method to decipher it. Therefore, a cryptanalyst would have to use a different approach to crack this cipher. One thing to consider is that in this cipher, reversed plaintext digraphs correspond to reversed cipher text digraphs, so that would help pick out a few letters.

The Playfair cipher was actually used in World War II by the German army, but instead of using the regular cipher, they used a double Playfair which eliminated the weaknesses in the cipher. In the double Playfair, the first letter of the digraph would be in one grid and the second would be in the other. Therefore, reversed plaintext digraphs would not actually correspond to reversed cipher text digraphs. In addition, double letters could be present in the cipher text which can give a false pattern to a cryptanalyst.

The Playfair cipher is one that is very simple to utilize but time consuming and difficult to decipher. The main weakness is how easy it is to crack it if someone knows the keyword. Otherwise, it is one of the best ciphers to securely encrypt a message as long as your intended recipient knows the key. It is important to note that the keyword is vital. The security of the message depends on the mutual understanding of the key between the sender and recipient and as little written evidence of it as possible.

I will leave you with this:

TAZSQVRMIPPBLMDQDYRIRFEPDATAQLMCRCPQAFTAFAVAMIIDLMALEOIMERVTHFSVKZ

This post is part of a series of essays on the history of cryptography produced by students at Vanderbilt University in honor of the release of The Imitation Game, a major motion picture about the life of British codebreaker and mathematician Alan Turing. The students wrote these essays for an assignment in a first-year writing seminar taught by mathematics instructor Derek Bruff.  For more information on the cryptography seminar, see the course blog.  And for more information on The Imitation Game, which opens in the US on November 28, 2014, see the film’s website.

Sources:

Akins, T. Playfair Cipher. (n.d.). Retrieved October 15, 2014.

Banerjee, J. (2014, August 15). Charles Wheatstone (1802-1875). Retrieved October 15, 2014.

Christensen, C. (2006, January 1). Playfair Cipher. Retrieved October 15, 2014.

Lyons, J. Playfair Cipher. (n.d.). Retrieved October 15, 2014.

Handwritten Russian Cipher Stumps FBI

By Riley Dankovich (Guest Contributor)

FBI (2008). The hollow nickel handed to the Brooklyn paperboy

In the wake of World War II, when cryptography had largely become mechanized, no one expected one of the most difficult-to-crack ciphers to be one created using pencil and paper.

In the summer of 1953, a young boy in Brooklyn received payment for a newspaper sale — unlike ordinary payment, one of the nickels was hollow. Something about the nickel seemed strange to the boy; he threw it to the ground, where it promptly split open. Inside was a piece of microfilm with 10 columns of numbers. Within days, word had reached a detective about the hollow nickel, which was quickly turned over to the FBI. The nickel, it turns out, was given to the paperboy by the wife of a Russian spy.

For four years, the FBI struggled with this cipher. They referred to the case as the “Hollow Nickel Case” (Rudolph), as they knew next to nothing else about the cipher text on the piece of microfilm, and had no further cipher text. Fortunately for the FBI, in 1957, a man approached them, declaring that he was a Russian intelligence officer, and wanted to defect. This man was Reino Häyhänen, codenamed “VICTOR,” from which the VIC Cipher, as this cipher came to be called, derives its name. After nearly four years without making much progress, Häyhänen’s defection was the FBI’s lucky break.

Likely the most complex pen and paper cipher ever created, the technical name for the VIC Cipher would be “a ‘straddling bipartite monoalphabetic substitution superenciphered by modified double transposition’” (Kahn). Most hand ciphers are either substitution ciphers, in which the letters are substituted for either other letters or numbers, or transposition ciphers, in which the order of the letters is scrambled. As cryptography became more advanced, cryptographers began to combine the two. The VIC Cipher contains not only a substitution and two transpositions, but also is passed through a straddling checkerboard to obtain the substitution, and then split in half (bipartite). Though this all seems incredibly complicated, the agent enciphering the text needed only to remember four simple key words or phrases, making messages much simpler to encipher for the Russians than to decipher for foreign intelligence.

The Straddling Checkerboard

A straddling checkerboard is a manner in which to obtain a more complex substitution, one that is therefore more difficult to decipher. It needs a keyword, which, in the case of the VIC Cipher, was СНЕГОПА, or “snowfall” in Russian. The numbers 0-9 are scrambled and placed above a ten-column-by-four-row grid.

Riley Dankovich (2014). Straddling checkerboard using the keyword СНЕГОПА (“snowfall”)

Under the numbers, the keyword (СНЕГОПА) is placed in the first row, leaving the last three columns blank. In the next three rows, the rest of the Russian alphabet follows, including a “.” and a “,” as well as the symbols Н/Ц, П/Л, Н/Т, and ПВТ, each of which have a meaning helpful to decipherment. The three numbers above the blanks left by the keyword are placed at the beginning of the second, third, and fourth rows. The letters in the first row, the keyword, will be enciphered as the numbers at the top of their subsequent columns. Any letter in the other rows, however, will be enciphered as two numbers: first, the number at the beginning of its row, and then the number at the top of its column. The word СПОСИБО (“thank you”) would be enciphered as 5 9 8 5 8 20 65 8. Before the plaintext is run through the straddling checkerboard, it is bisected. As a bisected cipher, the plaintext is cut into two parts in some random place, and the first half is attached to the end of the last half. The symbol H/T is placed before the true beginning of the cipher.

Next Comes Transposition Tables

After being run through the straddling checkerboard, what is now the cipher text is run through two transposition tables. This cipher uses three pieces of information (the first twenty letters of a popular Russian song, the date of Allied victory over Japan, and Häyhänen’s personal identification number) to generate a string of seemingly random numbers. These numbers determine the number of columns and rows in the tables, and several other minor factors. The cipher manipulates these three pieces of information, which have all been converted to numbers, using arithmetic modulo 10 and chain arithmetic. In modulo 10 arithmetic, once two numbers are added, the digit in the tens place is dropped. In chain arithmetic, numbers in a series are added continually until a desired series length is reached.

Riley Dankovich (2014). Beginning of Transposition Table 2, with disruption areas outlined

If the original series is, for example, 4, 9, 5, 3 7, the first two digits, 4 and 9, are added together (dropping the tens digit) to get 3, which is then added to the end of the series. Then the second and third digits, 9 and 5, are added to get 4, to get a series of 4, 9, 5, 3, 7, 3, 4, … until the desired series length (one of the factors determined by the seemingly random numbers) is reached. The numbers obtained from the straddling checkerboard are arranged in the first transposition table and then taken out in a different order and put into the second table. The numbers are taken in order from this table to form the final ciphertext.

Transposition ciphers, even without added manipulations, are difficult to decipher, though less so with the use of a strong computer. Because a transposition cipher simply rearranges the letters, the number of possible plaintexts can be determined easily, though the correct one is difficult to determine. If a cipher text has only 10 letters, it will have 10! (10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1) possible arrangements. This amounts to upwards of three million possibilities, and the VIC cipher is a great deal longer than 10 letters.

FBI (2008). The original cipher text of the VIC Cipher on microfilm

The VIC Cipher that Häyhäden explained to the FBI was sent to him from the Soviet Union soon after he arrived in the United States. Far from containing sinister instructions, the beginning of the decoded message read (in Russian): “We congratulate you on a safe arrival. We confirm the receipt of your letter to the address “V repeat V” and the reading of letter number 1” (Rudolph). Knowing the mechanism of this cipher, however, allowed the FBI to arrest, among others, Colonel Rudolf Ivanovich Abel, a Russian spy. He was sentenced to prison on three counts of conspiracy. As written in the FBI’s article Rudolph Ivanovich Abel (Hollow Nickel Case), “an investigation which had started with a newsboy’s hollow nickel ultimately resulted in the smashing of a Soviet spy ring.”

This cipher, though written with the simplest of utensils, pencil and paper and some arithmetic, stumped the United States’ foremost intelligence bureau for four years. Without the defection of Häyhänen, the world would still probably see the VIC Cipher as only 1035 numbers on microfilm (Kahn).Widely regarded as “the most complex hand-operated cipher ever seen,” the VIC Cipher was, to put it simply, an astronomically impressive feat of cryptographic skill.

 

This post is part of a series of essays on the history of cryptography produced by students at Vanderbilt University in honor of the release of The Imitation Game, a major motion picture about the life of British codebreaker and mathematician Alan Turing. The students wrote these essays for an assignment in a first-year writing seminar taught by mathematics instructor Derek Bruff.  For more information on the cryptography seminar, see the course blog.  And for more information on The Imitation Game, which opens in the US on November 28, 2014, see the film’s website.

Sources:

Book cipher, running key cipher, vic cipher and secom cipher. Retrieved October 14, 2014, from http://rageuniversity.com/PRISONESCAP...

Clarke, B. (2008, October 13). Hollow nickel spy case. Retrieved October 14, 2014, from http://www.prc68.com/I/NickelSpy.shtml

FBI. (2008). Hollow Nickel [Photograph], Retrieved October 14, 2014, from: http://commons.wikimedia.org/wiki/Fil...

FBI. (2008). Hollow Nickel Message [Photograph], Retrieved October 14, 2014, from: http://commons.wikimedia.org/wiki/Fil...

Kahn, D. (1993, September 22). Number one from Moscow. Retrieved October 14, 2014, from https://www.cia.gov/library/center-fo...

Rudolph Ivanovich Abel (hollow nickel case). (n.d.). Retrieved October 14, 2014, from http://www.fbi.gov/about-us/history/f...

Unsolved: Dorabella Cipher

By Sam MacKenzie (Guest Contributor)

In 1897, composer Edward Elgar sent an enciphered letter to his friend Miss Dora Penny, nicknamed Dorabella. The Dorabella Cipher may tell a tale of a secret affair between two unlikely lovers. It may be a casual letter to a friend who was important in the sender’s life. It may be gibberish. Regardless of what was said in the Dorabella Cipher, the contents have remained a mystery for over a century despite the interest shown by a countless number of cryptanalysts.

Edward Elgar was a famous composer, renowned for the famous graduation song Pomp and Circumstance March No. 1, who dabbled in other hobbies as well, including cryptography. Elgar was already m arried to a younger woman named Caroline who was once his student, but he undoubtedly enjoyed the company of Miss Dora. So much so, that in his famous work The Enigma Variations (a series of short musical portraits), he dedicated a section to her named Dorabella that featured woodwinds to represent her laughter (Peterson, 2009).

Long before Edward was known as a world famous composer, he wrote a mysterious letter, which continues to baffle the world to this day. On July 14, 1887, the letter appeared on Miss Penny’s doorstep. Miss Penny published the enciphered letter in her memoirs of Elgar to ask for possible solutions because she never had the slightest idea what it meant (Sams, 1970).

Clearly this cipher does not carry the same importance as the Enigma Machine (which was utilized by the Nazis to generate their encryptions), nor does it offer the same reward as decoding the Beale Ciphers (where the decoder would have been rewarded with a hefty amount of gold). Despite the lack of material significance, the Dorabella Cipher is still a popular mystery.

What does it mean?

Attempts to solve the Dorabella Cipher have been met with varying levels of success. The cipher features three rows and 24 different symbols of squiggles, totaling 80 characters. Most of the characters resemble the letter E, which could have something to do with Edward Elgar’s initials, EE. In 1887, computers were not yet spitting out complicated encoding systems, and it is unlikely that Edward could have expected Miss Penny to decipher anything too complicated. Therefore, most historians agree that it was enciphered using a substitution method (Kile, 2012).

In this case, a substitution encoding method would mean that each squiggly symbol represents a different letter of the alphabet. Although there are 26 letters in the alphabet and 24 different characters in the cipher, Edward could have easily worked around using infrequent letters such as “Z”, “X”, and others. Cryptanalysts commonly use frequency analysis, which matches the most common squiggles in the cipher to the most common letters (A, E, T), as a method to decode substitution ciphers. This frequency analysis has shown that a substitution cipher is plausible for the Dorabella Cipher (Kile, 2012). This finding supports the hypothesis that Elgar probably could not have employed a more complicated enciphering method. Despite the usage of frequency analysis, the cipher still remains unsolved.

Some challenges that cryptanalysts have encountered while attempting to solve the Dorabella cipher include the lack of cipher text and the private language that seems to have existed between Miss Penny and Edward Elgar. Frequency analysis is helpful for solving substitution ciphers, but is much less effective when there is so little cipher text to analyze. With less cipher text, the difference in frequency between the popular and unpopular symbols is too small to provide meaningful information about the symbols.

Additionally, Tony Gaffney, a renowned cryptanalyst, believes that their mixture of inside jokes and slang makes decoding the Dorabella cipher exceedingly difficult (Pelling, 2012). Decoding this letter would be similar to trying to decipher a letter written in an unknown language. Cryptanalysts are not only required to decipher the letter into plain English, they must also make random guesses at the inside jokes the letter could contain.

The mystery of the Dorabella cipher is not who sent the enciphered letter, or why, or how. Instead, the mystery is what was said in the letter. Most historians agree there were no sexual relations between Miss Penny and Edgar, since he was happily married, but they were very close and remained life long friends. When Edward was later questioned about the contents of the cipher by Miss Penny he reportedly said, “I thought you, of all people, would have guessed it” (Peterson, 2009). Perhaps the contents of the enciphered letter would allow us to better understand the mysterious relationship existing between Edward and Dora.

It is unlikely that the cipher carries relevant mathematical aspects, as neither Miss Penny nor Edward Elgar were mathematicians who were skilled with ciphers. Therefore, this cipher carries more historical significance. Many musicians would love to see into the mind of the famous composer, but that is beginning to seem more and more unlikely.

Will the cipher ever be solved? Generally, ciphers that are decoded the quickest are the ones that are the most urgent or have the highest reward. In either of these cases, the cipher receives a large amount of effort and resources. On the other hand, the Dorabella Cipher has no reward and no urgency, but rather is considered a hobby for idealists who enjoy a good story. As a result, it is doubtful that this cipher will be decoded considering the resources already unsuccessfully applied to trying to decode it.. It seems the mystery will remain unsolved, an inside joke for Elgar alone.

This post is part of a series of essays on the history of cryptography produced by students at Vanderbilt University in honor of the release of The Imitation Game, a major motion picture about the life of British codebreaker and mathematician Alan Turing. The students wrote these essays for an assignment in a first-year writing seminar taught by mathematics instructor Derek Bruff.  For more information on the cryptography seminar, see the course blog.  And for more information on The Imitation Game, which opens in the US on November 28, 2014, see the film’s website.

Sources:

Peterson, E. (2009, May 1). Unsolved Mysteries: The Dorabella Cipher [Web log]. Retrieved from: http://www.puzzlehead.org/2009/05/uns...

Kile, J. (2012, June 14). The Dorabella Cipher and a Possible Method for Deciphering [Web log]. Retrieved from: http://mysteriouswritings.com/the-dor...

Pelling, N. (2012). Dorabella Cipher [Web log]. Retrieved from: http://www.ciphermysteries.com/the-dorabella-cipher

Sams, E. (1970). Elgar’s Cipher Letter to Dorabella. The Musical Times, Vol. 111. Retrieved from: http://www.jstor.org/stable/956733

Image Sources:

Dorabella Cipher Image (photograph). (2011). Retrieved: October 30, 2014. From: http://commons.wikimedia.org/wiki/File:Dorabella-cipher-image.gif

Cynicalview (photographer). (2011). Envelope (photograph). Retrieved: November 11, 2014. From: https://www.flickr.com/photos/castorg...

Napoleon’s Guide to Improperly Using Cryptography

By Sarah Giordano (Guest Contributor)

Portrait de Napoléon Bonaparte en premier consul by Jean Auguste Dominique Ingres, Wikimedia Commons, Public Domain

For all his military genius, the one idea that Napoleon could not quite seem to grasp was the importance of cryptography. Most prominently, this failing was seen on the battleground of the Peninsular Wars in Iberia, where the French Empire and the British battled for dominance. Here, flurries of messages were passed amongst army units, often containing information about key military maneuvers or enemy tactics. British cryptanalysts frequently preyed upon French messages, capturing them to see what they could learn. To ensure the security of these messages, the use of strong codes and ciphers was critical. Unfortunately for the French Empire, Napoleon had to learn this lesson the hard way.

The glaring lapse in cryptography on the part of the French army was evident during the capture of one of their officers, General Franceschi, in the Iberian Peninsula. When captured, Franceschi was carrying a letter to Napoleon’s brother, the current King of Spain (Wellesley, 1837). One would think that a letter passing between allied rulers containing military information would be well protected by the strongest ciphers that the French army offered. However, it was not protected at all; with Franchesci’s capture, enemies of the French had instant access to the contents of Napoleon’s letter (Wellesley, 1837). The first lesson that the French needed learn about cryptography: use it.

From the Army of Portugal Code to the Great Paris Cipher

At this point Napoleon began to rethink his methods of security and tasked the French army with creating a large code. The one they created, called the Army of Portugal Code, was not simple; it used approximately 150 numbers, each of which represented either a letter or a word (Bertrand, Heyningen, n.d.). Unfortunately for the French, the British deciphered it in record time. In 1811, a man by the name of Major George Scovell sat down armed only with a beginner’s guide to cryptography and a few captured French messages (Urban, 2001B). Within two days, he had uncovered the current encryption system of the French, giving the advantage to the British and their allies once again.

Evidently, the Bonaparte brothers needed a huge cipher, riddled with dead ends, traps, and tricks in order to effectively confuse their enemies. Thus, at the end of 1811, the Great Paris Cipher, “Le Grande Chiffre de Paris”, was born from the minds of unknown French cryptographers.

The Great Paris Cipher was leaps ahead of the Army Code of Portugal. For instance, the cipher had few underlying patterns, only consisting of a table with words and letters followed by the number with which they were encoded (Urban, 2001 B). The table consisted of approximately 1400 numbers, which served to further increase the security (Urban, 2001 A). A cipher this large should have remained impenetrable for quite some time, because it was nearly impossible to figure out using the common decryption techniques of frequency analysis.

Essentially, frequency analysis, the fundamental decryption method of the time, consists of determining the number of times cipher text symbols appear so that one can determine which symbol corresponds to what “real”, also known as plaintext, letter. For example, if the number ‘4’ appears the most times in an encrypted letter, one might determine that the number 4 stands for the plaintext letter ‘e’, as e is the most common letter both in English and French (Urban, 2001 B). However, in the Great Paris Cipher a single letter would take on multiple numbers according to how frequently the letter was found in the language, a method which is known as homophonic substitution (Urban, 2001 A). Instantly, this renders frequency analysis useless because the frequency of one number in the cipher does not accurately represent the entire frequency of a letter in the plaintext.

To make it even more complicated, some numbers stood for nothing; they were simply included in the cipher text to make enemies even more confused. These “nulls”, as they were termed, were specifically inserted at the ends of words to thwart a common decryption technique of studying similar endings to cipher text words in search of linguistic patterns (Bertrand, Heyningen, n.d.).

Moreover, the Great Paris Cipher added another layer of complexity and variety by technically acting as both a code and a cipher (Bayart, V. &F., n.d.). This meant that a specific number could either be the encryption of a word or phrase (which would make it a code) or it could be the encryption of a syllable or a single letter (which would be described as a cipher). Enemy cryptanalysts would have difficulty discovering which number(s) corresponded to which words because words could be encrypted in many ways: with a number for each letter, for each syllable, for the entire word, or some combination thereof.

Indeed, “Le Grand Chiffre de Paris” was formidable in size and complexity, and had no noticeable underlying patterns. In truth, it seemed like all the security Napoleon needed.

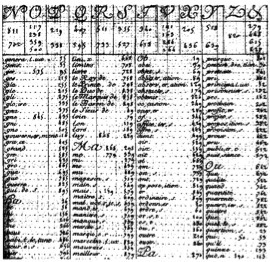
Le Grand Chiffre, Cryptologia, Wikimedia Commons Public Domain

Breaking the Great Paris Cipher

Yet, merely a year after the birth of this cipher, it was broken by Major Scovell, the same man who had broken the Army Code of Portugal. In truth, the Great Paris Cipher found its flaw not in its structure but in its use. In essence, the French were simply too lazy and overconfident in the cipher’s security to use it properly. Instead of encrypting messages using the cipher, the French army would only encrypt part of a message in an effort to cut down on the time spent using the cipher (Bayart, V. & F., n.d.). They mistakenly thought that their cipher would be strong enough to keep the full meaning of their messages a secret. By leaving some words of their message in common French, they provided a cryptanalyst like Scovell with an invaluable foothold, or “crib”, into their cipher.

Essentially, Scovell could use the words in plain text to take an educated guess at what the message might be, leading him to deduce what some encrypted words meant (Urban, 2001 A). Moreover, if the French left a verb out in the open, Scovell could easily decrypt the words around it by analyzing its conjugation (Urban, 2001 B). Slowly as Scovell gathered more cipher text, the number of cribs he collected increased until finally the cipher was completely broken. With this broken cipher, the British gained a serious edge in the Peninsular Wars. Keeping their discovery a secret, they could now collect and decrypt messages containing critical information for the French, resulting in serious repercussions for Napoleon. Using the information gained from “Le Grand Chiffre”, the British beat the French in the final battle for control of Spain (Bertrand, Heyningen, n.d.)

Although heralded as a strategic genius, Napoleon never recognized the importance of cryptography. Even when the French finally developed a competent encryption technique, they made the mistake of trusting in it so much that it was not properly utilized. Had the French sent fewer messages and encrypted the entirety of their letters, “Le Grand Chiffre” could have been nearly unbreakable. The British may not have defeated the French, and Spain might not have been thrust into the hands of revolutionaries instead of remaining under the rule of the current king. Instead, Napoleon practically threw away his information and his advantages. It wasn’t all for naught, however; from the mistakes of the French Empire, the world learned exactly what not to do while passing secret messages.

This post is part of a series of essays on the history of cryptography produced by students at Vanderbilt University in honor of the release of The Imitation Game, a major motion picture about the life of British codebreaker and mathematician Alan Turing. The students wrote these essays for an assignment in a first-year writing seminar taught by mathematics instructor Derek Bruff.  For more information on the cryptography seminar, see the course blog.  And for more information on The Imitation Game, which opens in the US on November 28, 2014, see the film’s website.

Sources:

Bayart, V. & F. Le Grand Chiffre de Paris (n.d.). Retrieved October 15, 2014, from http://www.bibmath.net/crypto/index.p...

Bertrand, C., & Heyningen, E. Secrets and Spies: The Great Paris Cipher. (n.d.). Retrieved October 15, 2014, from http://www.nationalarchives.gov.uk/spies/ciphers/scovell/default.htm

Urban, Mark. (2001 A.) The Man Who Broke Napoleon’s Codes: The Story of George Scovell. London: Faber and Faber.

Urban, M. (2001B, October 24). Wellington’s Lucky Break. Retrieved October 15, 2014.

Wellesley, A., & Gurwood, J. (1837). Dispatches of the Field Marshall the Duke of Wellington,  K.G.: During His Various Campaigns in India, Denmark, Portugal, Spain, the Low Countries, and France (pp. 498-499). John Murray, Albemarle Street.

The Emperor Changes His Mind

By Pamela Toler (Regular Contributor)

Emperors tend to be known for their military conquests: Alexander the Great, Julius Caesar, Genghis Khan, Napoleon.  The emperor Ashoka, who ruled the Maurya empire of India from 269 to 232BCE, is best known for his conversion to Buddhism and subsequent rejection of military aggression .

In the early years of his reign, Ashoka was a successful warrior who expanded the borders of his empire to  include most of modern Afghanistan, Bangladesh, India and Pakistan–an area larger than any other Indian ruler would command.

In 261, Ashoka led a brutal expedition against the neighboring kingdom of Kalinga (modern Orissa). Sickened by the loss of life, he converted to Buddhism and proclaimed his conversion to his subjects in a series of inscriptions engraved on rocks and pillars throughout his kingdom, the 3rd century BCE equivalent of billboards. In what are now known as the “Ashokan edicts”*, which appear to have been written by the emperor himself, he outlined his new dedication to “moral conquest” in place of military campaigns and rules for running a Buddhist kingdom.

In pursuit of his Buddhist ideals, Ashoka banned the animal sacrifices that were an important part of the Vedic religion, reduced the consumption of meat in the palace, and replaced the royal pastime of hunting with pilgrimages to Buddhist holy places. Despite his support of the Buddhist principle of ahimsa (non-violence) at a personal level, Ashoka never wholly embraced pacifism; he guaranteed the peace of his enormous empire with an army that included 600,000 foot soldiers, thirty thousand cavalry and nine thousand war elephants.

When modern India gained its independence in 1947, the new state chose the cluster of four lions that serve as the capital on the Ashokan pillar at Sarnath as its emblem. The choice was intended as a statement of India’s commitment to religious tolerance within a secular state.

*You can read a translation of the edicts here.

Image credit: mkistryn / 123RF Stock Photo

This post first appeared at Wonders & Marvels on 18 July 2013.

Shakespeare’s Secrets: A Hidden Cipher in Literature’s Greatest Works?

By Kristin Davis (Vanderbilt University)

William Shakespeare has for centuries been considered one of the greatest literary figures of all time, but a secret cipher hidden within the very pages of his plays may tell an exceedingly different story, one of forbidden marriages, a forgotten prince, and most of all, the genius of one man: Francis Bacon.

Born in sixteenth century England, Sir Francis Bacon was not only Lord Chancellor of England under James I, but was also a brilliant philosopher (British Broadcasting Company, 2012). Though not appreciated in his time, one of Bacon’s greatest achievements was a simple cipher he incorporated in his written works called the Baconian cipher (Sherman, 2010). The Baconian cipher does not possess great strength against decryption; instead its immense power and intrigue resides in its ability to make mystery lie, or appear to lie, in everything.

While most ciphers’ strengths dwell in the difficulty of finding the key to unlock a pattern, the Baconian cipher’s power lies in the challenge of uncovering its existence (Sherman, 2010). The cipher is only a simple substitution cipher in which one letter (or group of letters) stands for one other letter. The letters never change what they stand for as long as the same key is used throughout a message (Worley III, 2003). The Baconian cipher employs this substitution method by assigning a string of five letters consisting of only a’s and b’s to each letter in the alphabet. The arrangement of a’s and b’s in the five letter sequence determines the alphabet letter in the message (Worley III, 2003).

If a message contained only strings of a’s and b’s, it would be quite obvious to a cryptologist that some sort of cipher was used. Francis Bacon’s genius lies not in this simple substitution cipher, but in the fact that his cipher could be wielded to make, in Bacon’s own words, “anything mean anything” (Sherman, 2010). With the extra twist of steganography, which is concealing messages through deception, a-form and b-form can be two types of anything, from black and white to plus and minus, not just text (Sherman, 2010).

In Bacon’s traditional method, he replaced a’s and b’s with a-form fonts and b-form fonts (Worley III, 2003). For example, an enciphered message would be created by writing a seemingly innocuous message then changing the font of the letters so that bolded letters represent a’s and italicized letters represent b’s (Worley III, 2003). To decipher the message, the recipient would identify the a-forms and b-forms and use Bacon’s key to determine the alphabet letter signified by the string of five forms.

Innocuous Message

This is a Baconian cipher text

Cipher Text

Codes

C   /    O   /   D   /   E   /  S

aaaba/abbab/aaabb/aabaa/baaab

Process of Enciphering

aaaba/abbab/aaabb/aabaa/baaab

This i/s a Bac/onian/ ciphe/r text

Steganography

This is a Baconian cipher text

Being at its base only a substitution cipher, the method needed to break the plain cipher requires only knowledge of letter frequencies in the English language (Singh). To break the cipher, one first needs to accomplish the most challenging task of identifying the cipher is being employed. Next, one separates the letters of the message into groups of five and identifies the pattern of a-forms and b-forms. Because one five-letter group stands for one alphabet letter, one looks up the known frequencies of letters in English and matches them up with the frequency each five-letter group appears in the message (Worley III, 2003). For example, if the pattern “aabba” appears twelve percent of the time in the message, and the letter that appears twelve percent of the time in English is “e,” it can be inferred that “aabba” stands for “e.” Though cryptanalysis seems simple, this assumes the cryptologist first knows the cipher exists. Without a careful eye, a cryptologist could pass over the cipher not knowing its existence or spend years fruitlessly and frustratingly looking for something that was never there.

The unique complexity and mystery of the Baconian cipher has enticed cryptologists for generations to find patterns in chaos and hidden messages in everything from poetry, music, and most famously, Shakespeare. Though Bacon’s cipher was never adopted for military purposes, and Bacon only created it for his own amusement, his cipher took the literary world by storm (Sherman, 2010). Much like seeing pictures in the clouds or faces on the moon, cryptography enthusiasts began to see hidden a-form and b-form letters in everything.

One of the most famous results of Bacon’s cipher was widely considered “The Greatest of Literary Problems” (Sherman, 2010). After Shakespeare’s plays were written, literary analysts began to doubt that William Shakespeare of Stratford had been the true playwright (Sherman, 2010). The anti-Stratforians, as they called themselves, argued that Shakespeare, the uneducated, barely literate peasant, could not have produced such grand works (Baxter, 1915, p. 548). A promising alternative to the Stratford Shakespeare was Sir Francis Bacon (Sherman, 2010). After the discovery of De Augmentis, in which Bacon himself explains the workings of his cipher explicitly, literary analysts scoured the Shakespeare plays for the Baconian cipher (Friedman, 1957, p. 189).

In the early twentieth century, a prominent figure in the search, schoolteacher Elizabeth Wells Gallup, claimed to have broken the Baconian cipher found in the Shakespeare plays by analyzing the original folios to produce “alphabet classifiers” that determined whether a letter was an a-form or b-form (Sherman, 2010). Gallup deciphered pieces of text that seemed to indicate that Francis Bacon not only wrote the works historically contributed to Shakespeare, but also works of Spenser, Peele and Green, and Marlowe (Gallup, 1910, p. 17). Most consequential of all was that the cipher text claimed that the Virgin Queen Elizabeth I was no virgin at all, but actually the mother of Francis Bacon (Gallup, 1910, p. 6). This history-altering revelation meant that Bacon would have been the rightful heir to the throne and therefore the last Tudor, not Elizabeth (Gallup, 1910, p. 6). During Elizabeth Gallup’s time, even well respected thinkers such as Mark Twain, Walt Whitman, Sigmund Freud, Henry James, Henry Miller, and Helen Keller were “Baconians” (Sherman, 2010). As Gallup’s theories generated interest within the general public, millionaire businessman George Fabyan organized a group of cryptographers who worked on, as Fabyan explained, “wrestling from Nature, her secrets” (Sherman, 2010).

Fabyan not only greatly expanded Gallup’s work on the Shakespeare ciphers, but also more importantly introduced a young William Friedman to Francis Bacon’s ciphers (Sherman, 2010). Starting as an assistant to Gallup, Friedman began to doubt the methods used to decipher the texts (Friedman, 1957, p. 210). William Friedman and his wife, Elizebeth Friedman, began to notice inconsistencies in Gallup’s method of determining a-form letters and b-form letters (Friedman, 1957, p. 210). Friedman observed that often only Gallup would be able to see the differences in fonts and would often change her methods to “fix errors” to make the cipher text intelligible (Friedman, 1957, p. 210). Though Friedman would later disprove Gallup’s methods altogether and determine the Shakespeare project futile, this first exposure to the world of ciphers created the man that would soon go on to be one of history’s greatest cryptographers (Sherman, 2010).

Friedman was such a proponent to the development of cryptography that he not only coined the term “cryptanalysis,” but also served as chief cryptographer of United States for more than thirty years, co-invented the US Army’s best cipher machine, broke the Japanese PURPLE code in World War II, and wrote papers that gave cryptography its mathematical foundations (Sherman, 2010). Throughout his life, Friedman remained fascinated by the Baconian cipher that began his career.

While a colonel in the army, Friedman kept on his desk a picture of soldiers to whom he had just taught a class about cryptography. Though at first the picture seems like any other war memento, on closer examination one might notice how some soldiers are not looking at the camera. An even sharper eye might notice that the pattern of looking towards and away from the camera spells out Friedman’s favorite Baconian axiom: knowledge is power (Sherman, 2010).

Though Bacon may not have enciphered messages that he authored Shakespeare’s plays or was the son on Queen Elizabeth I, Bacon’s cipher and the reactions to it changed not only the field of cryptography, but also the future of technology. Bacon, with his two-letter alphabet, was, according to the Center Cryptologic History, “the inventor of the binary code that forms the basis of modern … computers” (Sherman, 2010). Though the authorship mystery of Shakespeare may never be solved, Bacon’s cipher created the career of one of the greatest cryptographers of all time and formed the basis for binary code, the language of computers. Francis Bacon’s ability to hide mystery within the mundane forced others to look past the obvious to appreciate the mystery within everyday life.

This post was first published in December 2012. This post is part of a series of essays on the history of cryptography produced by students at Vanderbilt University.  The students wrote these essays for an assignment in a first-year writing seminar taught by mathematics instructor Derek Bruff.  The essays are shared here, in part, to give the students an authentic and specific audience for their writing.  For more information on this cryptography seminar, see the course blog.

Did you enjoy this post? If so, check back for more Cryptography posts November 17th-November 21st.

Works Cited

Baxter, J. P. (1915). The Greatest of Literary Problems. New York: Houghton Mifflin Company. British Broadcasting Company. (2012). Francis Bacon. Retrieved October 27, 2012, http://www.bbc.co.uk/history/historic_figures/bacon_francis.shtml.

Friedman, W. F. (1957). Shakespearean Ciphers Examined. Cambridge: Cambridge University Press.

Gallup, E. W. (1910). Concerning the Bi-literal Cypher of Sir Francis Bacon: Pros and Cons of the Controversy. London, England: Howard Publishing Company.

Sherman, W. H. (2010). How to Make Anything Signify Anything. Cabinet (40).

Singh, S. (n.d.). Substitution Ciphers. Retrieved October 27, 2012, from The Black Chamber: http://www.simonsingh.net/The_Black_Chamber/crackingsubstitution.html.

Worley III, G. G. (2003, February 26). Baconian Cipher. Retrieved October 25, 2012, from Computer Science at the University of Central Florida: http://www.cs.ucf.edu/~gworley/files/baconian_cipher.txt

Pictures

Bacon, F. (1623). De Augmentis Scientiarum Libri IX. London: In officina Ioannis Hauiland.

Bacon, F., Spedding, J., Ellis, R. L., & Heath, D. D. (1882). The Works of Francis Bacon. London: Longman.

 

Did They or Didn’t They?

By John Oller (Guest Contributor)

Kate, in later years, wearing the “306” pin.

In this age of emails, texts, and smartphone cameras, it is harder and harder for public figures to avoid having their extra-marital affairs and other sexual hi-jinx laid bare for the world to see (just ask Tiger Woods, Anthony Weiner, or Justin Bieber). But in days of yore, unless amorous letters were written (and preserved, not burned), determining whether a well-known person was, in fact, guilty of adultery or sexual indiscretion was largely a guessing game.

In researching my biography of Kate Chase Sprague, the beautiful and politically ambitious daughter of Salmon P. Chase, Abraham Lincoln’s treasury secretary, I confronted the same question that faced earlier biographers: whether she had an extra-marital affair with Roscoe Conkling, the powerful U.S. senator from New York. Rumors of their liaison persisted for years until the summer of 1879, when Kate’s husband, William Sprague discovered his wife having breakfast with Senator Conkling at the Sprague mansion in Narragansett, Rhode Island. Sprague allegedly chased Conkling out of the house with a shotgun, creating a scandal that made the front page of every major newspaper in the country.

Despite Kate’s insistent denials, most historians have assumed that she and Conkling were lovers. Still, no one has ever had any proof. But I found several new pieces of evidence that, I believe, significantly bolster the affirmative case. Most of these are mementoes and photographs of Kate that have been passed down to her descendants over the years and never seen outside her family.

Lovers’ Tokens

The breastpin given to Kate by Roscoe Conkling

For example, I was shown a small breastpin that Kate kept until her death consisting of a miniature silver sword drawn through a set of diamonds that formed the number “306.” It represents the 306 delegates at the 1880 Republican National Convention who, at Conkling’s urging, continued to support the losing effort of Ulysses S. Grant to gain the presidential nomination for a third term. In photographs taken years later, Kate can be seen wearing her “306” pin, given to her by Conkling—an indication of her strong feelings for him (image above). Indeed, the pin is one of only a handful of mementoes she kept until her death.

She also kept a bracelet with an inscription in German that reads, “I lock you into my heart and throw the key into the Rhine and now you must always be within me.” The giver is not identified, but Conkling is the logical candidate. She was photographed wearing the bracelet in 1877, the same year she and Conkling are believed to have traveled together in Europe. Upon his return to America, Conkling extolled the people and “land of the Rhine.”

Kate, in 1877, wearing (on her right wrist) a bracelet given to her by Conkling.

I also was shown a short parting note Conkling wrote to Kate in 1883, around the time of their amicable breakup, in which, quoting Shakespeare, he alludes to the love and happiness they had found in each other, but which could not survive the envy and scorn and prurient interest of lesser people.

Finally, I discovered in the research papers of an earlier biographer the previously unpublished fact that Kate tried to visit Conkling at his deathbed in 1888. She was prevented from doing so by his wife, from whom he had long been estranged.

One might argue that none of these discoveries, in themselves, proves the existence of a physical relationship. But together with the previously known facts, I believe that this new evidence establishes the case, in the eyes of history, beyond a reasonable doubt.

 

John Oller is the author of American Queen: The Rise and Fall of Kate Chase Sprague—Civil War “Belle of the North” and Gilded Age Woman of Scandal.

 

 

The history of tampons – in ancient Greece?

by Helen King

Did ancient Greek women use tampons? It’s clear that women today are curious as to what women in the past did when they were menstruating. As regular readers of Wonders & Marvels know, I did my PhD on ancient Greek menstruation and I also feel I’m on a crusade to clear up some of the ‘creative’ (actually, just plain wrong) statements about Hippocrates that are out there on the WWW. In a previous post here I’ve looked at the ‘using rags’ theory. But recently I’ve come across another claim that seems to originate in the marketing for Tampax but which has been picked up without any critical analysis by a lot of other sites. The original source seems to be the claim on the Tampax site that “The Greek physician Hippocrates, writing in the fifth century B.C., described another type of tampon, which was made of lint wrapped around lightweight wood” .

Leaving aside the ‘did Hippocrates write anything in the Hippocratic corpus?’ question, can we really find anything like that in ancient Greek medicine? Variations on other internet sites that seem to derive from the Tampax claim include “as described in the writings of Hippocrates, a tampon used pieces of wood, wrapped [sic] fiber” and, with a cheerful disregard for the whole Greece/Rome thing, “Apparently Hippocrates documented that Roman women used wooden sticks wrapped with lint.”. I like that ‘apparently’. Someone else has realised that there is an important question about how we are supposed to know this: what’s the evidence?

The wonderful Museum of Menstruation site, which makes a real effort to identify its sources and to engage with historians working on the topic, is much more cautious, talking about ancient usage of “tampons for contraception, which possibly means that women also used material as tampons to control menstruation.” Note that ‘possibly’. Just because you insert things into the vagina for one purpose doesn’t mean you do it for another; although at least, as the founder of the Museum of Menstruation, Harry Finley, pointed out when we had a chat about this, it shows that there is no sort of taboo attached to such insertion.

Tampons up the nose?

So what about the ancient Greek medical texts that came to be known as the ‘Hippocratic corpus’? In the Hippocratic treatises Joints and Instruments of Reduction, when the nose is fractured, the physician is told to roll up lint in a rag or in thin Carthaginian leather (chosen because it is so soft) and insert this into the nose. The ancient Greek word used here is motos. This, as here, can mean lint for dressing wounds, but in its entry for motos the indispensable ancient Greek-English dictionary by Liddell, Scott and Jones (known cheerfully to classicists as ‘LSJ’) also gives ‘tent, tampon’. Is this where the imaginary ‘Hippocratic tampon’ comes from?

Now, in a medical context, a tent is not somewhere you spend the night during an outdoor vacation, but an expansible plug of soft material for opening up an orifice. In medical English, tampons also have a rather different meaning to that which we now assume. Before Tampax came on the scene, there were tampons, but not as we know them. A tampon was simply a plug of some sort, used to stop bleeding, and inserted into a wound or, if menstrual flow seemed excessive, into the vagina. The word comes from the verb ‘to tamp’ meaning to stop up a hole, or to push down – you can ‘tamp’ tobacco into the bowl of a pipe before smoking it. But when Tampax came on the scene as a commercial product, the word was shifted more narrowly towards menstruation, so today’s near-exclusive application of the word to menstrual products is the result of the invention of Tampax.

Does the motos feature in the Hipppocratic treatises on women’s bodies? Yes, but not in the context of a way of absorbing normal menstrual flow. In Diseases of Women 1 (Littré 8.138.12) it means some soothing lint applied to the mouth of the womb and in book 2 of the same treatise (Littré 8.332.18) there are three motoi of increasing size inserted into the mouth of the womb because the neck of the womb is hard and closed so the menstrual blood can’t get out. Similarly, although different words are used, when a remedy needs to be inserted into the vagina – for example, beetles to irritate the womb and bring on a delayed menstrual period – it is wrapped up in wool first. But none of these uses concerns management of normal menstrual flow.

The pig-pen?

There is one other isolated reference worth mentioning. This comes not from the ancient Greek medical texts but from the fifth-century BC comic playwright Aristophanes (Lysistrata 1073) who refers once to men looking like they are wearing a ‘pig-pen’ (choirokomeion) round their thighs. One of the ancient words for the female external genitalia is choiros – piggy – used for the genitals of a young girl, or – if depilated – of an older woman. So is the joke here about wearing something around your piggy that looks quite bulky – such as a home-made menstrual pad? The word choiros itself has an interesting masculine/feminine dimension, in that if it is used in the masculine it means ‘female genitalia’ but in the feminine, it’s ‘pig’! In fact, when the men who look like they are wearing pig-pens open their cloaks, what they are hiding under there are their erect penises.

If anyone would have made a choiros joke like this, it would be Aristophanes. He was well aware of the entertainment value of the word. Another of his plays, Acharnians, has an extended joke about a poor man who is trying to sell his daughters as ‘piggies’.  And in support of my suggestion, I can cite LSJ, not a dictionary to make daring assumptions. It gives as the meaning of choirokomeion – on this occasion only – ‘bandage used by females’. So is this what men called a menstrual pad, or what women called it? In any case, if we follow this line of reasoning, it could be further evidence that menstrual management in ancient Greece was by home-made pads of rags, rather than tampons.

 

For more on Aristophanes, try James Robson, Aristophanes: an Introduction (London: Bristol Classical Press, 2009) and watch the free online series ‘The Birth of Comedy’ that starts here.