Greg Ross's Blog, page 14

After You

A train engine pulling four cars meets a train engine pulling three cars. There’s a short spur next to the main track, but it can hold only one engine or one car at a time. A car cannot be joined to the front of an engine. What’s the most expeditious way for the two trains to pass one another?

This sounds fairly simple, but the solution is surprisingly involved. In presenting the problem in his Cyclopedia of 5000 Puzzles, Tricks, and Conundrums (1914), Sam Loyd wrote that it “shows the primitive way of passing trains before the advent of modern methods, and the puzzle is to tell just how many times it is necessary to back or reverse the directions of the engines to accomplish the feat, each reversal of an engine being counted as a move in the solution.”

Loyd’s solution requires 33 steps:

Image: Wikimedia Commons

“L train picks up its third car and goes on its way rejoicing.”

DIY

In 1888, on reading that the villanelle requires “an elaborate amount of care in production, which those who read only would hardly suspect existed,” British philologist W.W. Skeat tossed off this one:

It’s all a trick, quite easy when you know it,
As easy as reciting A B C,
You need not be an atom of a poet.

If you’ve a grain of wit, and want to show it,
Writing a villanelle — take this from me —
It’s all a trick, quite easy when you know it.

You start a pair of rimes, and then you “go it”
With rapid-running pen and fancy free;
You need not be an atom of a poet.

Take any thought, write round it and below it,
Above or near it, as it liketh thee;
It’s all a trick, quite easy when you know it.

Pursue your task, till, like a shrub, you grow it,
Up to the standard size it ought to be;
You need not be an atom of a poet.

Clear it of weeds, and water it, and hoe it,
Then watch it blossom with triumphant glee.
It’s all a trick, quite easy when you know it;
You need not be an atom of a poet.

Navel Warfare

Image: Wikimedia Commons

Another mistake there may be in the Picture of our first Parents, who after the manner of their posterity are both delineated with a Navel. … Which notwithstanding cannot be allowed, … that in the first and most accomplished piece, the Creator affected superfluities, or ordained parts without use or office.

… Now the Navel being a part, not precedent, but subsequent unto generation, nativity or parturition, it cannot be well imagined at the creation or extraordinary formation of Adam, who immediately issued from the Artifice of God; nor also that of Eve, who was not solemnly begotten, but suddenly framed, and anomalously proceeded from Adam.

— Thomas Browne, Pseudodoxia Epidemica, 1646

Hypertension

New English verb tenses, offered by David Morice in a November 1986 Word Ways article:

Future past perfect: I will have had walked
Progressive conditional: I would have should have been walking
Future present past: He will does walked
Double future: He will will walk
Unconditional present: He could can walk
Obsessive progressive: He is being doing walking
Refractive future perfect: He did will was have walked
Superjunctive: He might be having been about to be walking

The Tortoise stepped ever so carefully across the finish line, just a moment before the Hare would have been about to be going to hop across it himself. ‘I won!’ she said. The Hare paused a moment, then replied, ‘Yes, Ms. Tortoise, in the next decade you will have been about to be going to be used to be having been doing being the winner of this race, but tomorrow we’ll have to do it again, for it’s two out of three, ma’am.’

Footwork

Thomas Jefferson coined the word pedicure (at least in the sense “a person responsible for pedicure”).

His memorandum book for February 7, 1785, reads “P[ai]d La Forest, pedicure 12f.”

(Thanks, Joseph.)

Poem

The sum of 2k – 4
From one to thirteen plus a score,
Over eleven,
Plus eighteen times seven,
Equals six cubed and not a bit more.

(Will Nediger, “Can Math Limericks Survive?”, Word Ways 37:3 [August 2004], 238.)

More math limericks.

Block Diagram

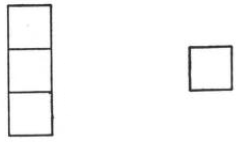
A tromino is a domino of three panels in a row, sized to cover three successive orthogonal squares of a checkerboard.

A monomino covers one square.

Is it possible to cover an 8×8 checkerboard with 21 trominoes and 1 monomino?

Yes. Color the board’s squares like so:

This gives us 22 gray, 21 black, and 21 white squares. We can accomplish our task if each tromino covers squares of three different colors.

Where shall we put the monomino? It can’t go in the bottom left square, for example, as that would leave us with 22 gray, 21 white, and 20 black squares. By symmetry we can also reject the board’s three other corner squares, which might equally well have been colored black, ruining our plan by the same reasoning.

Extending this idea, the monomino can’t go on any white or black square or on any square symmetric to a white or black square. Of the 22 gray squares on the board, only four are symmetric only to other gray squares. If the monomino is placed on one of these squares, the remainder of the board can be covered with 21 trominoes. A sample tiling is shown below.

From J.A.H. Hunter and Joseph S. Madachy, Mathematical Diversions, 1963.

“Ascot Waistcoat”

Prescott, press my Ascot waistcoat —
Let’s not risk it
Just to whisk it:
Yes, my Ascot waistcoat, Prescott.
Worn subfusc, it’s
Cool and dusk: it
Might be grass-cut
But it’s Ascot,
And it fits me like a gasket —
Ascot is the waistcoat, Prescott!
Please get
Off the spot of grease. Get
Going, Prescott —
Where’s that waistcoat?
It’s no task at
All, an Ascot:
Easy as to clean a musket
Or to dust an ivory tusk. It
Doesn’t take a lot of fuss. Get
To it, Prescott,
Since I ask it:
We can’t risk it —
Let’s not whisk it.
That’s the waistcoat;
Thank you, Prescott.

— David McCord

The Perfect Infinitive

“Let us take a typical case. A gentleman and his wife, calling on friends, find them not at home. The gentleman decides to leave a note of regret couched in a few well-chosen words, and the first thing he knows he is involved in this:

We would have liked to have found you in.

“Reading it over, the gentleman is assailed by the suspicion that he has too many ‘haves,’ and that the whole business has somehow been put too far into the past. … He takes an envelope out of his pocket and grimly makes a list of all the possible combinations, thus getting:”

We would have liked to have foundWe would have liked to findWe would like to have foundWe would like to findWe had hoped to have been able to have found

“If he has married the right kind of woman, she will hastily scratch a brief word on a calling card, shove it under the door, and drag her husband away.”

— James Thurber, “Ladies’ and Gentlemen’s Guide to Modern English Usage,” 1931

Piecework

In his Canterbury Puzzles of 1907, Henry Dudeney posed a now-famous challenge: How can you cut an equilateral triangle into four pieces that can be reassembled to form a perfect square?

Dudeney’s beautiful solution was accompanied by a rather involved geometric derivation. It seems unlikely that he worked this out laboriously in approaching an answer to the problem, but how then did he reach it?

Here’s one possibility: If a strip of squares is draped adroitly over a strip of triangles, their intersection forms a wordless proof of the task’s feasibility:

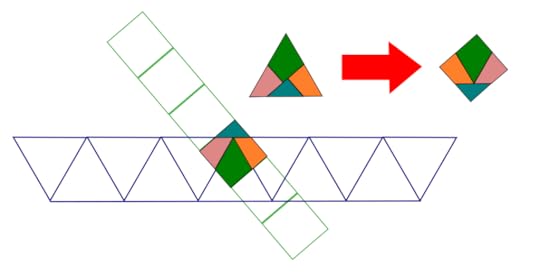Image: Wikimedia Commons

Whether that was Dudeney’s path to the solution is not known, but it appears at least plausible.