Allen B. Downey's Blog: Probably Overthinking It, page 5

Political Alignment, Affiliation, and Attitudes

Is there a growing gender gap in the U.S?

Alignment

A recent article in the Financial Times suggests that among young people there is a growing gender gap in political alignment on a spectrum from liberal to conservative.

In last week’s post, I tried to replicate this result using data from the General Social Survey. I generated the following figure, which shows the percentage of liberals minus the percentage of conservatives from 1988 to 2021, among people 18 to 29 years old. The analysis is in this Jupyter notebook.

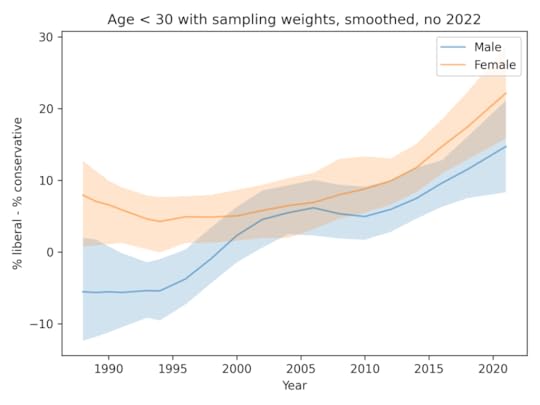
Women are more likely to say they are liberal by 5-10 percentage points. But there is little or no evidence that the gap is growing.

Party Affiliation

This figure shows the percentage of Democrats minus the percentage of Republicans from 1988 to 2021. The analysis is in this Jupyter notebook.

Women are more likely than men to say they are Democrats. In the 1990s, the gap was almost 20 percentage points. Now it is only 5-10 percentage points. So there’s no evidence this gap is growing — if anything, it is shrinking.

Attitudes and beliefs

To quantify political attitudes, I will take advantage of a method I used in Chapter 12 of Probably Overthinking It. In the General Social Survey, I chose 15 questions where there is the biggest difference in the responses of people who identify as liberal or conservative. Then I estimated the number of conservative responses from each respondent.

The following figure shows the average number of conservative responses for young men and women since 1974. The analysis is in this Jupyter notebook.

Men give slightly more conservative responses than women, on average, but the gap is small and consistent over time — there is no evidence it is growing.

In summary, GSS data provides no support for the claim that there is a growing gender gap in political alignment, affiliation, or attitudes.

Extremes, outliers, and GOATS

The video from my PyData Global 2023 talk, Extremes, outliers, and GOATS, is available now:

The slides are here.

There are two Jupyter notebooks that contain the analysis I presented:

Chapter 4 of Probably Overthinking ItAn exploration of Gaussian and lognormal models for anthropomorphic measurements

Here’s the abstract:

The fastest runners are much faster than we expect from a Gaussian distribution, and the best chess players are much better. In almost every field of human endeavor, there are outliers who stand out even among the most talented people in the world. Where do they come from?

In this talk, I present as possible explanations two data-generating processes that yield lognormal distributions, and show that these models describe many real-world scenarios in natural and social sciences, engineering, and business. And I suggest methods — using SciPy tools — for identifying these distributions, estimating their parameters, and generating predictions.

This talk is based on Chapter 4 of Probably Overthinking It. If you liked the talk, you’ll love the book

Thanks to the organizers of PyData Global and NumFOCUS!

Is the Ideology Gap Growing?

This tweet from John Burn-Murdoch links to an article in the Financial Times (FT), “A new global gender divide is emerging”, which includes this figure:

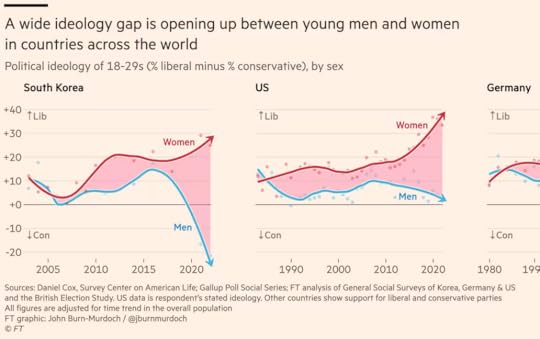
The article claims:

In the US, Gallup data shows that after decades where the sexes were each spread roughly equally across liberal and conservative world views, women aged 18 to 30 are now 30 percentage points more liberal than their male contemporaries. That gap took just six years to open up.

The figure says it is based on General Social Survey data and the text says it’s based on Gallup data, so I’m not sure which it is. UPDATE: In this tweet Burn-Murdoch explains that the figure shows Gallup data, backfilled with GSS data from before the Gallup series began.

And I don’t know what it means that “All figures are adjusted for time trend in the overall population”. UPDATE: In this tweet, Burn-Murdoch explains that the adjustment mentioned in the figure is to subtract off the overall trend. In the notebook for this article, I apply the same adjustment, but it does not change my conclusions.

Anyway, since I used GSS data in several places in Probably Overthinking It, this analysis did not sound right to me. So I tried to replicate the analysis with GSS data.

I conclude:

The GSS data does not look like the figure in the FT.Women are a more likely to say that they are liberal, by 5-10 percentage points.The only evidence that the gap is growing depends entirely on a data point from 2022 that is probably an error.If we drop the 2022 data and apply moderate smoothing, we see no evidence that the gap is growing.

Most of the functions in this notebook are the ones I used to write Probably Overthinking It. All of the notebooks for that book are available in this repository.

Click here to run this notebook on Colab

GSS Data

I’m using data from the General Social Survey (GSS), which I previous cleaned in this notebook. The primary variable we’ll use is polviews, which asks:

We hear a lot of talk these days about liberals and conservatives. I’m going to show you a seven-point scale on which the political views that people might hold are arranged from extremely liberal–point 1–to extremely conservative–point 7. Where would you place yourself on this scale?

The points on the scale are Extremely liberal, Liberal, and Slightly liberal; Moderate; Slightly conservative, Conservative, and Extremely conservative.

I’ll lump the first three points into “Liberal” and the last three into “Conservative”

All respondents

The following figure shows the percentage who says they are liberal minus the percentage who say they are conservative, grouped by sex.

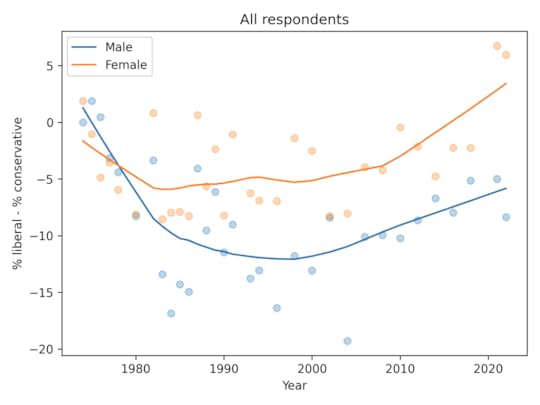
In the general population, women are more likely to say they are liberal by 5-10 percentage points. The gap might have increased in the most recent data, depending on how seriously we take the last two points in a noisy series.

Just young people

Now let’s select people under 30.

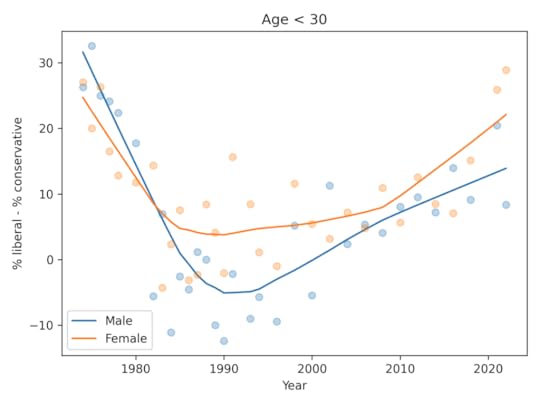
The trends here are pretty much the same as in the general population. Women are more likely to say they are liberal by 5-10 percentage points.

It’s possible that the gap has grown in the most recent data, but the evidence is weak and depends on how we draw a smooth curve through noisy data.

Anyway, there is no evidence the trend for men is going down — as in the FT graph — and the gap in the most recent data is nowhere near 30 percentage points.

With Sampling Weights

In the previous figures, I did not take into account the sampling weights, partly to keep the analysis simple and partly because I didn’t expect them to make much difference.

And I was mostly right, except for men in 2022 – and as we’ll see, there is almost certainly something wrong with that data point.

In this figure, the shaded area is the 90% CI of 101 weighted resamplings, the line is the median of the resamplings, and the points show the unweighted data. We only have weighted data since 1988, since that’s how far back the wtssps variable goes.

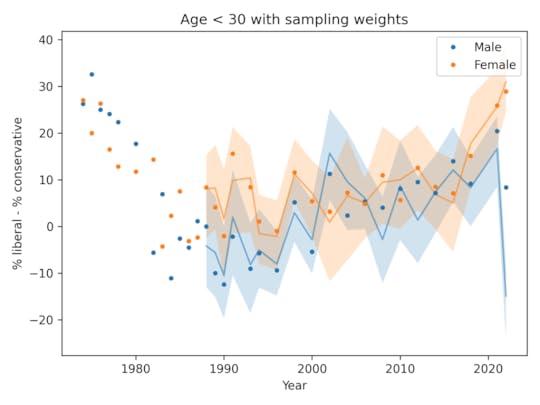
In most cases, the unweighted data falls in the CI of the weighted data, but for male respondents in 2022, the weighting moves the needle by almost 30 percentage points.

So something is not right there. I think the best option is to drop the 2022 data, but just for completeness, let’s see what happens if we apply some smoothing.

Resampling and smoothing

Here’s a version of the same plot with moderate smoothing, dropping the unweighted data.

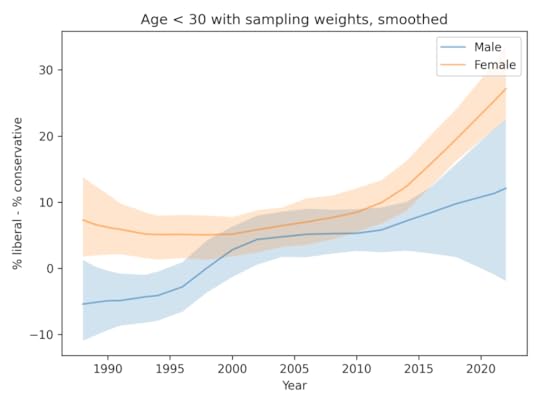
You could argue that this figure shows evidence for an increasing gap, but the error bounds are very wide, and as we’ll see in the next figure, the entire effect is due to the likely error in the 2022 data.

Resampling and smoothing without 2022

Finally, here’s the analysis I think is the best choice, dropping the 2022 data for both men and women.

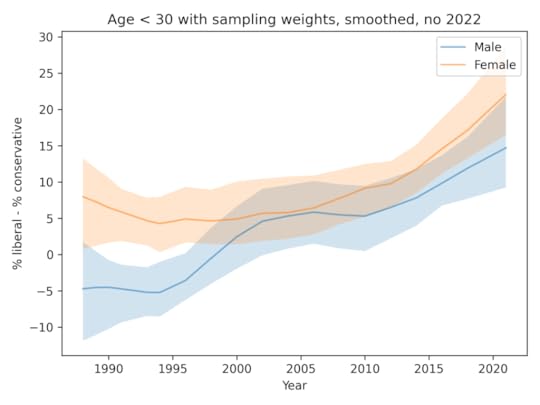
In summary:

Since the 1990s, both men and women have become more likely to identify as liberal.Women are more likely to identify as liberal by 5-10 percentage points.There is no evidence that the ideology gap is growing.

Probably Overthinking It Notebooks

To celebrate one month since the launch of Probably Overthinking It, I’m releasing the Jupyter notebooks I used to create the book. There’s one per chapter, and they contain all of the code I used to do the analysis and generate the figures. So if you are curious about the details of anything in the book, the notebooks are here!

If you — or someone you love — is teaching statistics this semester, please let them know about this resource. I think a lot of the examples in the book are good for teaching.

And if you are enjoying Probably Overthinking It, please help me spread the word:

Recommend the book to a friend.Write reviews on Amazon, Goodreads, or your favorite book site.Talk about it on social media.Request it from your local library.Order it from your local bookstore or suggest they carry it.

It turns out that writing a book is the easy part — finding an audience is hard!

The Center Moves Faster Than You

In May 2022, Elon Musk tweeted this cartoon:

The creator of the cartoon, Colin Wright, explained it like this:

At the outset, I stand happily beside ‘my fellow liberal,’ who is slightly to my left. In 2012 he sprints to the left, dragging out the left end of the political spectrum […] and pulling the political “center” closer to me. By 2021 my fellow liberal is a “woke ‘progressive,’ ” so far to the left that I’m now right of center, even though I haven’t moved.”

The cartoon struck a chord, which suggests that Musk and Wright are not the only ones who feel this way.

As it happens, this phenomenon is the topic of Chapter 12 of Probably Overthinking It and this post from April 2023, where I use data from the General Social Survey to describe changes in political views over the last 50 years.

The chapter includes this figure, which shows how beliefs have changed among people who consider themselves conservative, moderate, and liberal.

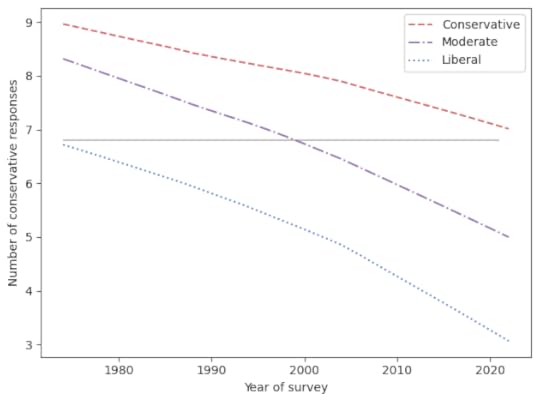
All three groups give fewer conservative responses to the survey questions over time. (To see how I identified conservative responses, see the talk I presented at PyData 2022. The technical details are in this Jupyter notebook.)

The gray line represents a hypothetical person whose views don’t change. In 1972, they were as liberal as the average liberal. In 2000, they were near the center. And in 2022, they were almost as conservative as the average conservative.

Using the same methods, I made this data-driven version of the cartoon.

The blue circles show the estimated conservatism of the average self-identified liberal; the red squares show the average conservative, and the purple line shows the overall average.

The data validate Wright’s subjective experience. If you were a little left of center in 2008 and you did not change your views for 14 years, you would find yourself a little right of center in 2022.

However, the cartoon is misleading in one sense: the center did not shift because people on the left moved far to the left. It moved primarily because of generational replacement. On the conveyor belt of demography, when old people die, they are replaced by younger people — and younger people hold more liberal views.

On average people become a little more liberal as they age, but these changes are small and slow compared to generational replacement. That’s why many people have the experience reflected in the cartoon — because the center moves faster than them.

For more on this topic, you can read Chapter 12 of Probably Overthinking It. You can get a 30% discount if you order from the publisher and use the code UCPNEW. You can also order from Amazon or, if you want to support independent bookstores, from Bookshop.org.

Or you might like this talk I presented at PyData NYC, this podcast, and this online article at Brilliant.org.

How Many Books?

If you like this article, you can read more about this kind of Bayesian analysis in Think Bayes.

Recently I found a copy of Probably Overthinking It at a local bookstore and posted a picture on Twitter. Aubrey Clayton replied with this question:

It’s a great question with what turns out to be an interesting answer. I’ll summarize the results here, but if you want to see the calculations, you can run the notebook on Colab.

Assumptions

Suppose you are the author of a book like Probably Overthinking It, and when you visit a local bookstore, like Newtonville Books in Newton, MA, you see that they have two copies of your book on display.

Is it good that they have only a few copies, because it suggests they started with more and sold some? Or is it bad because it suggests they only keep a small number in stock, and they have not sold. More generally, what number of books would you like to see?

To answer these questions, we have to make some modeling decisions. To keep it simple, I’ll assume:

The bookstore orders books on some regular cycle of unknown duration.At the beginning of every cycle, they start with k books.People buy the book at a rate of λ books per cycle.When you visit the store, you arrive at a random time t during the cycle.

We’ll start by defining prior distributions for these parameters, and then we’ll update it with the observed data.

Priors

For some books, the store only keeps one copy in stock. For others it might keep as many as ten. If we would be equally unsurprised by any value in this range, the prior distribution of k is uniform between 1 and 10.

If we arrive at a random point in the cycle, the prior distribution of t is uniform between 0 and 1, measured in cycles.

Now let’s figure the book-buying rate is probably between 2 and 3 copies per cycle, but it could be substantially higher – with low probability. We can choose a lognormal distribution that has a mean and shape that seem reasonable. Here’s what it looks like.

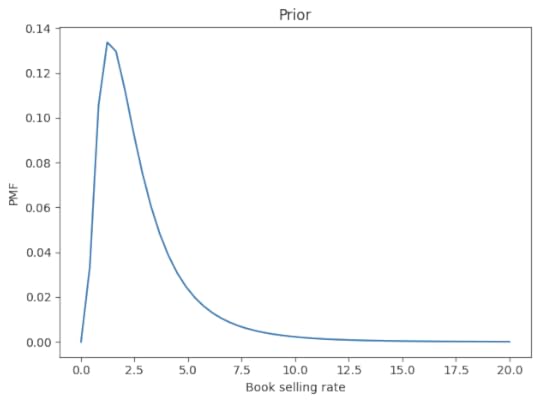
From these marginal prior distributions, we can form the joint prior. Now let’s update it.

The update

Now for the update, we have to handle two cases:

If we observe at least one book, n, the probability of the data is the probability of selling k-n books at rate λ over period t, which is given by the Poisson PMF.If there are no copies left, we have to add in the probability that the number of books sold in this period could have exceeded k, which is given by the Poisson survival function.

After computing these likelihoods for all possible sets of parameters, we do a Bayesian update in the usual way, multiplying the priors by the likelihoods and normalizing the result.

As an example, we’ll do an update with the hypothetically observed 2 books. Then, from the joint posterior, we can extract the marginal distributions of k and λ, and compute their means.

Seeing two books suggests that the store starts each cycle with 3-4 books and sells 2-3 per cycle. Here’s the posterior distribution of k compared to its prior.

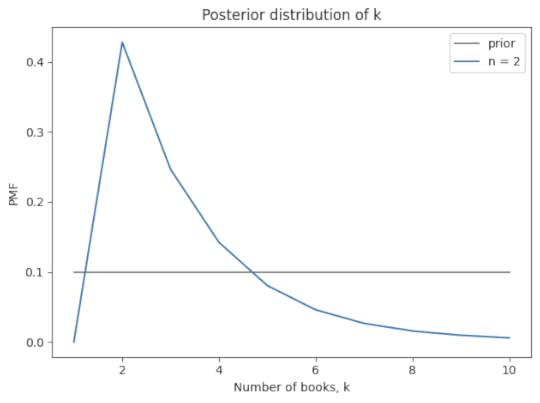
And here’s the posterior distribution of λ.

Seeing two books doesn’t provide much information about the book-selling rate.

Optimization

Now let’s consider the more general question, “What number of books would you most like to see?” There are two ways we might answer:

One answer might be the observation that leads to the highest estimate of λ. But if the book-selling rate is high, relative to k, the book will sometimes be out of stock, leading to lost sales.So an alternative is to choose the observation that implies the highest number of books sold per cycle.

Computing the second is a little tricky — you can see the details in the notebook. But with that problem solved, we can loop over possible values of n and compute for each one the posterior mean values of λ and the implied number of books sold per cycle.

Here’s the implied sales rate as a function of the observed number of books. By this metric, the best number of books to see is 0.

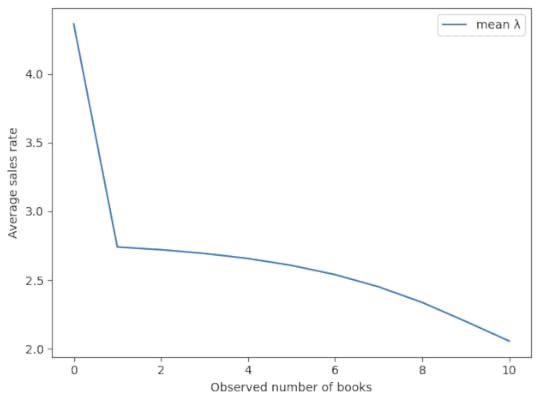
And here’s the implied number of books sold per cycle.

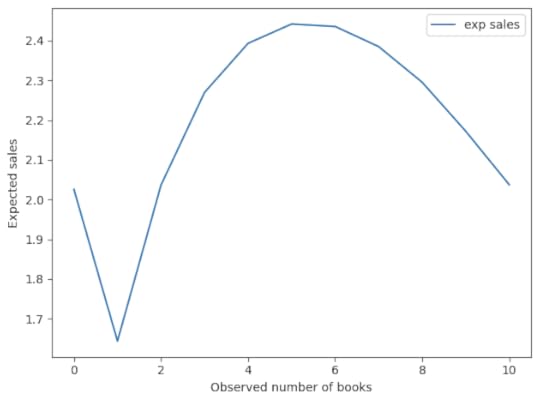
This result is a little more interesting. Seeing 0 books is still good, but the optimal value is around 5. The worst possibility is to see just one book.

Now, we should not take these values too literally, as they are based on a very small amount of data and a lot of assumptions – both in the model and in the priors. But it is interesting that the optimal point is neither 0 nor “as many as possible.

Thanks again to Aubrey Clayton for asking such an interesting question. If you are interesting in the history and future of statistical thinking, you might like his book, Bernoulli’s Fallacy.

previous

What are the odds?

Whenever something unlikely happens, it is tempting to ask, “What are the odds?”

In some very limited cases, we can answer that question. For example, if someone deals you five cards from a well-shuffled deck, and you want to know the odds of getting a royal flush, we can answer that question precisely. At least, we can if you are clearly referring to just this one hand.

But if you’ve been playing poker regularly for a decade and then one night you are dealt a royal flush, it might not be clear, when you ask the question, whether you mean the odds of getting a royal flush on one deal, or one evening of play, or some time in your career, or once in all of the poker hands that have every been deal. Those are different questions with very different answers — in fact, the first is close to 0 and the last is close to 1 (and known to be 1 in this universe).

So, even in a highly constrained environment like a poker game, answering questions like this can be tricky. It’s even worse in real life. Say you go to college in Massachusetts and then two years later you visit Paris, go for a walk in the Tuileries Garden, and run into a friend from college. What are the odds? Now we have to define both “in how many attempts?” and “odds of what?” Meeting this friend in this particular place? Or any old friend in any unexpected place?

Now let’s put all of this thinking to the test with an example, which is the most surprising thing that has happened to me since the time I ran into a college friend in Paris. Two days ago I was working on a heat vent in my house and wanted to attach this socket

to this screwdriver

But the socket takes a 1/4 inch square drive, and the screwdriver takes 1/4 inch hex bits. I figured there was probably an adapter that could connect them, but I didn’t have one. I thought about getting one, but then I found another way to do the job.

Two days later I went for a walk and about 30 yards from my house, in the middle of the street, I saw a small bit of metal that I picked up just to get it out of the way. And when I looked more closely at what is was — it was a 1/4 inch hex to 1/4 inch square drive adapter.

And here’s how it works.

So, what are the odds of that? I don’t know, but if you have a non-zero prior for the existence of a benevolent deity, you might want to update it.

Smoking Causes Cancer

In the preface of Probably Overthinking It, I wrote:

Sometimes interpreting data is easy. For example, one of the reasons we know that smoking causes lung cancer is that when only 20% of the population smoked, 80% of people with lung cancer were smokers. If you are a doctor who treats patients with lung cancer, it does not take long to notice numbers like that.

When I re-read that paragraph recently, it occurred to me that interpreting those number might not be as easy as I thought. To find out, I ran a Twitter poll. Here are the results:

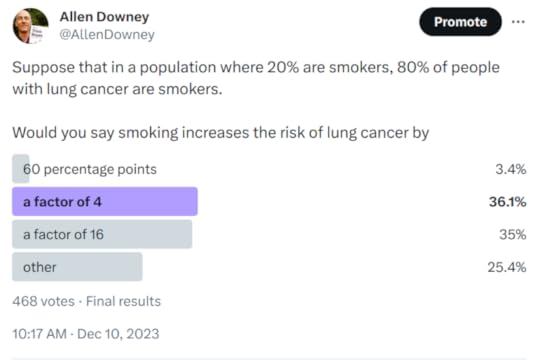
Some of the people who chose “other” said that there is not enough information — we need to know the absolute risk for one or both of the groups.

I think that’s not right — with just these two numbers, we can compute the relative risk of the two groups. There are a few ways to do it, but a good way to get started is to check each of the multiple choice responses.

Off the bat, “60 percentage points” is just wrong. If the lifetime risk of cancer was 20% in one group and 80% in the other, we could describe that difference in terms of percentage points. But those are not the numbers we were given, and the actual risks are much lower.

But “a factor of 4” is at least plausible, so let’s check it. Suppose that the actual lifetime risk of lung cancer for non-smokers is 1% — in that case the risk for smokers would be 4%. In a group of 1000 people, we would expect 800 non-smokers and 8 cases among them, and we would expect 200 smokers and 8 cases among them. Under these assumptions 50% of people with lung cancer would be smokers, but the question says it should be 80%, so this check fails.

Let’s try again with “a factor of 16”. If the risk for non-smokers is 1%, the risk for smokers would be 16%. Among 800 non-smokers, we expect 8 cases again, but among 200 smokers, now we expect 32. Under these assumptions, 80% of people with lung cancer are smokers, so 16 is the correct answer.

Here are the same numbers in a table.

NumberRiskCasesPercentNon-smoker8001%820%Smoker20016%3280%

Now, you might object that I chose 1% and 16% arbitrarily, but as it turns out it doesn’t matter. To see why, let’s assume that the risk is x for non-smokers and 16x for smokers. Here’s the table with these unknown risks.

NumberRiskCasesPercentNon-smoker800x800x20%Smoker20016x3200x80%

The percentage of cases among smokers is 80%, regardless of x.

Now suppose you are not satisfied with this guess-and-check method. We can solve the problem more generally using Bayes’s rule.

We are given p(smoker) = 20%, which we can convert to odds(smoker) = 1/4.And we are given p(smoker | cancer) = 80%, which we can convert to odds(smoker | cancer) = 4.

Applying Bayes’s rule, we have

odds(smoker | cancer) = odds(smoker) * p(cancer | smoker) / p(cancer | non-smoker)

Rearranging terms, we can solve for the risk ratio:

p(cancer | smoker) / p(cancer | non-smoker) = odds(smoker | cancer) / odds(smoker) = 16

That’s the answer I had in mind, but let me address an objection raised by one poll respondent, who chose “Other” because, “You can’t draw casual inferences from observational data without certain assumptions which I’m unwilling to make.”

That’s true. Even if the risk is 16x higher for smokers, that’s not enough to conclude that the entire difference, or any of it, is caused by smoking. It is still possible either:

(1) that the supposed effect is really the cause, or in this case that incipient cancer, or a pre-cancerous condition with chronic inflammation, is a factor in inducing the smoking of cigarettes, or (2) that cigarette smoking and lung cancer, though not mutually causative, are both influenced by a common cause, in this
case the individual genotype.

If you think that’s the stupidest thing you’ve ever heard, you can take it up with Sir Ronald Fisher, who actually made this argument with apparent sincerity in a 1957 letter to the British Medical Journal. I mention this in case you didn’t already know what an ass he was.

However, if we are willing to accept that smoking causes lung cancer, and is in fact responsible for all or nearly all of the increased risk, then we can use the data we have to answer a related question: if a smoker is diagnosed with lung cancer, what is the probability that it was caused by smoking?

To answer that, let’s assume that smokers are exposed at the same rate as non-smokers to causes of cancer other than smoking. In that case, their 16x risk would consist of 15x risk due to smoking and 1x risk due to other causes. So 15/16 cancers among smokers would be due to smoking, which is about 94%.

Some actual numbers

I rounded off the numbers in my example to make the math easy, so let’s see what the actual numbers are. “Smoking and Cancer“, one of the fact sheets published along with “The Health Consequences of Smoking—50 Years of Progress: A Report of the Surgeon General” includes this figure.

In the most recent interval, the relative risk was about 25x, and at that time about 20% of the U.S. population smoked. The lifetime risk of lung cancer is about 6%, including both smokers and non-smokers, so to find the lifetime risk for non-smokers, we can solve this equation for x:

p(smoker) x + p(non-smoker) (25 x) = 6%

0.8x + 0.2(25x) = 0.06

Which means the lifetime risk is about 1% for non-smokers and 25% for smokers. If we update the table with these numbers, we have

NumberRiskCasesPercentNon-smoker8001%814%Smoker20025%5086%

And with that, we can address another point raised by a Twitter friend:

By “smoking increases the risk of lung cancer” you could either mean relative to being a non-smoker or relative to the overall base rate of cancer (including a weighted average of smokers and non-smokers).

I meant the first (which is more common in epidemiology), but if we want the second, it’s about 25 / 6, which is a little more than 4.

Finally, looking at that figure you might wonder why the relative risk of smoking has increased so much. Based on my first pass through the literature, it seems like no one knows. There are at least three possibilities:

Over this period, cigarettes have been reformulated in ways that might make them more dangerous.As the prevalence of smoking has decreased, it’s possible that the number of casual smokers has decreased more quickly, leaving a higher percentage of heavy smokers.Or maybe the denominator of the ratio — the risk for non-smokers — has decreased.

In what I’ve read so far, the first explanation seems to get the most attention, but there doesn’t seem to be a clear causal path for it.The second and third explanations seem plausible to me, but I haven’t found the data to support them.

Causes of lung cancer in non-smokers include radon, second-hand smoke, asbestos, heavy metals, diesel exhaust, and air pollution. I would guess that exposure to all of them has decreased substantially since the 1960s. But it seems like we don’t have good evidence that the risk for non-smokers has decreased. That’s surprising, and a possible topic for a future post.

Happy Launch Day!

Today is the official publication date of Probably Overthinking It! You can get a 30% discount if you order from the publisher and use the code UCPNEW. You can also order from Amazon or, if you want to support independent bookstores, from Bookshop.org.

I celebrated launch day by giving a talk at PyData Global 2023 called “Extremes, outliers, and GOATs: On life in a lognormal world“. In my opinion, it went well! Here’s the abstract:

“The fastest runners are much faster than we expect from a Gaussian distribution, and the best chess players are much better. In almost every field of human endeavor, there are outliers who stand out even among the most talented people in the world. Where do they come from?

“In this talk, I present as possible explanations two data-generating processes that yield lognormal distributions, and show that these models describe many real-world scenarios in natural and social sciences, engineering, and business. And I suggest methods — using SciPy tools — for identifying these distributions, estimating their parameters, and generating predictions.”

My slides are available hereThe Jupyter notebook with the examples from Chapter 4 is hereAnd the notebook with the additional analysis for the talk is here

When the video is available, I will post it here.

Superbolts

Probably Overthinking It is available to predorder now. You can get a 30% discount if you order from the publisher and use the code UCPNEW. You can also order from Amazon or, if you want to support independent bookstores, from Bookshop.org.

Recently I read a Scientific American article about superbolts, which are lightning strikes that “can be 1,000 times as strong as ordinary strikes”. This reminded me of distributions I’ve seen of many natural phenomena — like earthquakes, asteroids, and solar flares — where the most extreme examples are thousands of times bigger than the ordinary ones. So the article about superbolts made we wonder

Whether superbolts are really a separate category, or whether they are just extreme examples from a long-tailed distribution, andWhether the distribution is well-modeled by a Student t-distribution on a log scale, like many of the examples I’ve looked at.

The SciAm article refers to this paper from 2019, which uses data from the World Wide Lightning Location Network (WWLLN). That data is not freely available, but I contacted the authors of the paper, who kindly agreed to share a histogram of data collected over from 2010 to 2018, including more than a billion lightning strokes (what is called a lightning strike in common usage is an event that can include more than one stroke).

For each stroke, the dataset includes an estimate of the energy released in 1 millisecond within a certain range of frequencies, reported in Joules. The following figure shows the distribution of these measurements on a log scale, along with a lognormal model. Specifically, it shows the tail distribution, which is the fraction of the sample greater than or equal to each value.

On the left part of the curve, the model predicts that there should be more strokes in the range near 10² J, which there might have been, but they were not detected. Other than that, we could conclude that the data are well-modeled by a lognormal distribution.

However, on this scale it is hard to tell whether the tail of the distribution fits the model. We can see more clearly if we put the y-axis on a log scale. Here’s what that looks like.

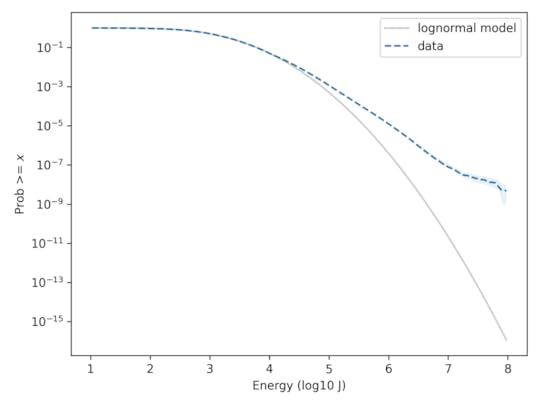
On this scale it’s apparent that the lognormal model seriously underestimates the frequency of superbolts. In this dataset, the fraction of strokes that exceed 10e7.9 J is about 6 per 10e9. According to the lognormal model, it would be about 3 per 10e16 — so it’s off by about 7 orders of magnitude.

In , I showed that a Student t-distribution on a log scale, which I call a log-t distribution, is a good model for several datasets like this one. Here’s the lightning data again with a log-t model I chose to fit the data.

With the y-axis on a linear scale, we can see that the log-t model fits the data as well as the lognormal or better. And here’s the same comparison with the y-axis on a log scale.

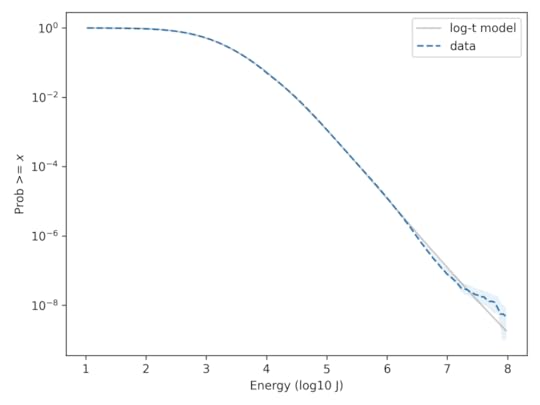
Here we can see that the log-t model fits the tail of the distribution substantially better. Even in the extreme tail, the data fall almost entirely within the bounds we would expect to see by chance.

One of the researchers who provided this data explained that if you look at data collected from different regions of the world during different seasons, the distributions have different parameters. And that suggests a reason the combined data might follow a t distribution, which can be generated by a mixture of Gaussian distributions with different variance.

I would not say that these data are literally generated from a t distribution. The world is more complicated than that. But if we are particularly interested in the tail of the distribution — as superbolt researchers are — this might be a useful model.

The details of my analysis are in this Jupyter notebook, which you can run on Colab.

Thanks to Professors Robert Holzworth and Michael McCarthy for sharing the data from their paper and reading a draft of this post (with the acknowledgement that any errors are my fault, not theirs).