Allen B. Downey's Blog: Probably Overthinking It, page 3
November 24, 2024
Download the World in Data
Our World in Data recently announced that they are providing APIs to access their data. Coincidentally, I am using one of their datasets in my workshop on time series analysis at PyData Global 2024. So I took this opportunity to update my example using the new API – this notebook shows what I learned.
Click here to run this notebook on Colab. It is based on Chapter 12 of Think Stats, third edition.
import numpy as npimport pandas as pdimport matplotlib.pyplot as pltAir TemperatureIn the chapter on time series analysis, in an exercise on seasonal decomposition, I use monthly average surface temperatures in the United States, from a dataset from Our World in Data that includes “temperature [in Celsius] of the air measured 2 meters above the ground, encompassing land, sea, and in-land water surfaces,” for most countries in the world from 1941 to 2024.
The following cells download and display the metadata that describes the dataset.
import requestsurl = (
"https://ourworldindata.org/grapher/"
"average-monthly-surface-temperature.metadata.json"
)
query_params = {
"v": "1",
"csvType": "full",
"useColumnShortNames": "true"
}
headers = {'User-Agent': 'Our World In Data data fetch/1.0'}
response = requests.get(url, params=query_params, headers=headers)
metadata = response.json()
The result is a nested dictionary. Here are the top-level keys.
metadata.keys()dict_keys(['chart', 'columns', 'dateDownloaded'])Here’s the chart-level documentation.
from pprint import pprintpprint(metadata['chart']){'citation': 'Contains modified Copernicus Climate Change Service information ' '(2019)', 'originalChartUrl': 'https://ourworldindata.org/grapher/av...', 'selection': ['World'], 'subtitle': 'The temperature of the air measured 2 meters above the ground, ' 'encompassing land, sea, and in-land water surfaces.', 'title': 'Average monthly surface temperature'}And here’s the documentation of the column we’ll use.
pprint(metadata['columns']['temperature_2m']){'citationLong': 'Contains modified Copernicus Climate Change Service ' 'information (2019) – with major processing by Our World in ' 'Data. “Annual average” [dataset]. Contains modified ' 'Copernicus Climate Change Service information, “ERA5 monthly ' 'averaged data on single levels from 1940 to present 2” ' '[original data].', 'citationShort': 'Contains modified Copernicus Climate Change Service ' 'information (2019) – with major processing by Our World in ' 'Data', 'descriptionKey': [], 'descriptionProcessing': '- Temperature measured in kelvin was converted to ' 'degrees Celsius (°C) by subtracting 273.15.\n' '\n' '- Initially, the temperature dataset is provided ' 'with specific coordinates in terms of longitude and ' 'latitude. To tailor this data to each country, we ' 'utilize geographical boundaries as defined by the ' 'World Bank. The method involves trimming the global ' 'temperature dataset to match the exact geographical ' 'shape of each country. To correct for potential ' "distortions caused by the Earth's curvature on a " 'flat map, we apply a latitude-based weighting. This ' 'step is essential for maintaining accuracy, ' 'especially in high-latitude regions where ' 'distortion is more pronounced. The result of this ' 'process is a latitude-weighted average temperature ' 'for each nation.\n' '\n' "- It's important to note, however, that due to the " 'resolution constraints of the Copernicus dataset, ' 'this methodology might not be as effective for ' 'countries with very small landmasses. In these ' 'cases, the process may not yield reliable data.\n' '\n' '- The derived 2-meter temperature readings for each ' 'country are calculated based on administrative ' 'borders, encompassing all land surface types within ' 'these defined areas. As a result, temperatures over ' 'oceans and seas are not included in these averages, ' 'focusing the data primarily on terrestrial ' 'environments.\n' '\n' '- Global temperature averages and anomalies are ' 'calculated over all land and ocean surfaces.', 'descriptionShort': 'The temperature of the air measured 2 meters above the ' 'ground, encompassing land, sea, and in-land water ' 'surfaces. The 2024 data is incomplete and was last ' 'updated 13 October 2024.', 'fullMetadata': 'https://api.ourworldindata.org/v1/ind...', 'lastUpdated': '2023-12-20', 'owidVariableId': 819532, 'shortName': 'temperature_2m', 'shortUnit': '°C', 'timespan': '1940-2024', 'titleLong': 'Annual average', 'titleShort': 'Annual average', 'type': 'Numeric', 'unit': '°C'}
The following cells download the data for the United States – to see data from another country, change country_code to almost any three-letter ISO 3166 country codes.
country_code = 'USA' # replace this with other three-letter country codesbase_url = (
"https://ourworldindata.org/grapher/"
"average-monthly-surface-temperature.csv"
)
query_params = {
"v": "1",
"csvType": "filtered",
"useColumnShortNames": "true",
"tab": "chart",
"country": country_code
}
from urllib.parse import urlencodeurl = f"{base_url}?{urlencode(query_params)}"temp_df = pd.read_csv(url, storage_options=headers)
In general, you can find out which query parameters are supported by exploring the dataset online and pressing the download icon, which displays a URL with query parameters corresponding to the filters you selected by interacting with the chart.
temp_df.head()EntityCodeyearDaytemperature_2mtemperature_2m.10United StatesUSA19411941-12-15-1.8780198.0162441United StatesUSA19421942-01-15-4.7765517.8489842United StatesUSA19421942-02-15-3.8708687.8489843United StatesUSA19421942-03-150.0978117.8489844United StatesUSA19421942-04-157.5372917.848984The resulting DataFrame includes the column that’s documented in the metadata, temperature_2m, and an additional undocumented column, which might be an annual average.
For this example, we’ll use the monthly data.
temp_series = temp_df['temperature_2m']temp_series.index = pd.to_datetime(temp_df['Day'])Here’s what it looks like.
temp_series.plot(label=country_code)plt.ylabel("Surface temperature (℃)");
Not surprisingly, there is a strong seasonal pattern. We can use seasonal_decompose from StatsModels to identify a long-term trend, a seasonal component, and a residual.
from statsmodels.tsa.seasonal import seasonal_decomposedecomposition = seasonal_decompose(temp_series, model="additive", period=12)We’ll use the following function to plot the results.
def plot_decomposition(original, decomposition): plt.figure(figsize=(6, 5)) plt.subplot(4, 1, 1) plt.plot(original, label="Original", color="C0") plt.ylabel("Original") plt.subplot(4, 1, 2) plt.plot(decomposition.trend, label="Trend", color="C1") plt.ylabel("Trend") plt.subplot(4, 1, 3) plt.plot(decomposition.seasonal, label="Seasonal", color="C2") plt.ylabel("Seasonal") plt.subplot(4, 1, 4) plt.plot(decomposition.resid, label="Residual", color="C3") plt.ylabel("Residual") plt.tight_layout()plot_decomposition(temp_series, decomposition)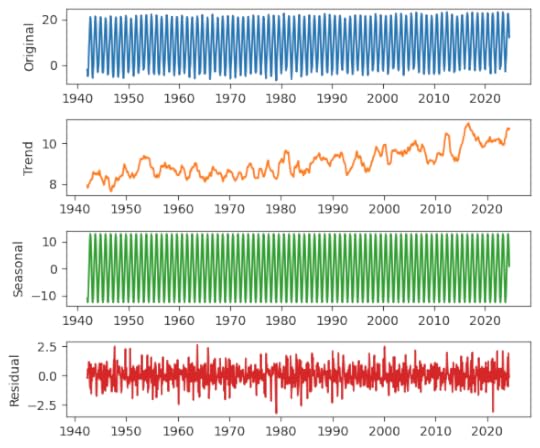
As always, I’m grateful to Our World in Data for making datasets like this available, and now easier to use programmatically.
November 19, 2024
What’s a Chartist?
Recently I heard the word “chartist” for the first time in my life (that I recall). And then later the same day, I heard it again. So that raises two questions:
What are the chances of going 57 years without hearing a word, and then hearing it twice in one day?Also, what’s a chartist?To answer the second question first, it’s someone who supported chartism, which was “a working-class movement for political reform in the United Kingdom that erupted from 1838 to 1857”, quoth Wikipedia. The name comes from the People’s Charter of 1838, which called for voting rights for unpropertied men, among other reforms.
To answer the first question, we’ll do some Bayesian statistics. My solution is based on a model that’s not very realistic, so we should not take the result too seriously, but it demonstrates some interesting methods, I think. And as you’ll see, there is a connection to Zipf’s law, which I wrote about last week.
Since last week’s post was at the beginner level, I should warn you that this one is more advanced – in rapid succession, it involves the beta distribution, the t distribution, the negative binomial, and the binomial.
This post is based on Think Bayes 2e, which is available from Bookshop.org and Amazon.
Click here to run this notebook on Colab.
Word FrequenciesIf you don’t hear a word for more than 50 years, that suggests it is not a common word. We can use Bayes’s theorem to quantify this intuition. First we’ll compute the posterior distribution of the word’s frequency, then the posterior predictive distribution of hearing it again within a day.
Because we have only one piece of data – the time until first appearance – we’ll need a good prior distribution. Which means we’ll need a large, good quality sample of English text. For that, I’ll use a free sample of the COCA dataset from CorpusData.org. The following cells download and read the data.
download("https://www.corpusdata.org/coca/sampl... zipfiledef generate_lines(zip_path="coca-samples-text.zip"): with zipfile.ZipFile(zip_path, "r") as zip_file: file_list = zip_file.namelist() for file_name in file_list: with zip_file.open(file_name) as file: lines = file.readlines() for line in lines: yield (line.decode("utf-8"))We’ll use a Counter to count the number of times each word appears.
import refrom collections import Counterpattern = r"[ /\n]+|--"counter = Counter()for line in generate_lines(): words = re.split(pattern, line)[1:] counter.update(word.lower() for word in words if word)The dataset includes about 188,000 unique strings, but not all of them are what we would consider words.
len(counter), counter.total()(188086, 11503819)To narrow it down, I’ll remove anything that starts or ends with a non-alphabetical character – so hyphens and apostrophes are allowed in the middle of a word.
for s in list(counter.keys()): if not s[0].isalpha() or not s[-1].isalpha(): del counter[s]This filter reduces the number of unique words to about 151,000.
num_words = counter.total()len(counter), num_words(151414, 8889694)Of the 50 most common words, all of them have one syllable except number 38. Before you look at the list, can you guess the most common two-syllable word? Here’s a theory about why common words are short.
for i, (word, freq) in enumerate(counter.most_common(50)): print(f'{i+1}\t{word}\t{freq}')1 the 4619912 to 2379293 and 2314594 of 2173635 a 2033026 in 1533237 i 1379318 that 1238189 you 10963510 it 10371211 is 9399612 for 7875513 on 6486914 was 6438815 with 5972416 he 5768417 this 5187918 as 5120219 n't 4929120 we 4769421 are 4719222 have 4696323 be 4656324 not 4387225 but 4243426 they 4241127 at 4201728 do 4156829 what 3563730 from 3455731 his 3357832 by 3258333 or 3214634 she 2994535 all 2939136 my 2939037 an 2858038 about 2780439 there 2729140 so 2708141 her 2636342 one 2602243 had 2565644 if 2537345 your 2464146 me 2455147 who 2350048 can 2331149 their 2322150 out 22902There are about 72,000 words that only appear once in the corpus, technically known as hapax legomena.
singletons = [word for (word, freq) in counter.items() if freq == 1]len(singletons), len(singletons) / counter.total() * 100(72159, 0.811715228893143)Here’s a random selection of them. Many are proper names, typos, or other non-words, but some are legitimate but rare words.
np.random.choice(singletons, 100)array(['laneer', 'emc', 'literature-like', 'tomyworld', 'roald', 'unreleased', 'basemen', 'kielhau', 'clobber', 'feydeau', 'symptomless', 'channelmaster', 'v-i', 'tipsha', 'mjlkdroppen', 'harlots', 'phaetons', 'grlinger', 'naniwa', 'dadian', 'banafionen', 'ceramaseal', 'vine-covered', 'terrafirmahome.com', 'hesten', 'undertheorized', 'fantastycznie', 'kaido', 'noughts', 'hannelie', 'cacoa', 'subelement', 'mestothelioma', 'gut-level', 'abis', 'potterville', 'quarter-to-quarter', 'lokkii', 'telemed', 'whitewood', 'dualmode', 'plebiscites', 'loubrutton', 'off-loading', 'abbot-t-t', 'whackaloons', 'tuinal', 'guyi', 'samanthalaughs', 'editor-sponsored', 'neurosciences', 'lunched', 'chicken-and-brisket', 'korekane', 'ruby-colored', 'double-elimination', 'cornhusker', 'wjounds', 'mendy', 'red.ooh', 'delighters', 'tuviera', 'spot-lit', 'tuskarr', 'easy-many', 'timepoint', 'mouthfuls', 'catchy-titled', 'b.l', 'four-ply', "sa'ud", 'millenarianism', 'gelder', 'cinnam', 'documentary-filmmaking', 'huviesen', 'by-gone', 'boy-friend', 'heartlight', 'farecompare.com', 'nurya', 'overstaying', 'johnny-turn', 'rashness', 'mestier', 'trivedi', 'koshanska', 'tremulousness', 'movies-another', 'womenfolks', 'bawdy', 'all-her-life', 'lakhani', 'screeeeaming', 'marketings', 'girthy', 'non-discriminatory', 'chumpy', 'resque', 'lysing'], dtype='Now let’s see what the distribution of word frequencies looks like.
Zipf’s LawOne way to visualize the distribution is a Zipf plot, which shows the ranks on the x-axis and the frequencies on the y-axis.
freqs = np.array(sorted(counter.values(), reverse=True))n = len(freqs)ranks = range(1, n + 1)Here’s what it looks like on a log-log scale.
plt.plot(ranks, freqs)decorate( title="Zipf plot", xlabel="Rank", ylabel="Frequency", xscale="log", yscale="log")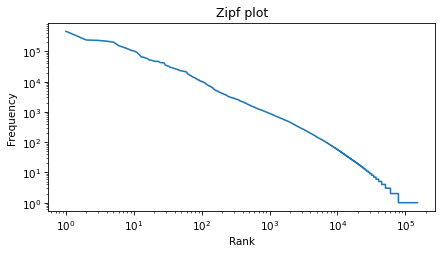
Zipf’s law suggest that the result should be a straight line with slope close to -1. It’s not exactly a straight line, but it’s close, and the slope is about -1.1.
rise = np.log10(freqs[-1]) - np.log10(freqs[0])rise-5.664633515191604run = np.log10(ranks[-1]) - np.log10(ranks[0])run5.180166032638616rise / run-1.0935235433575892The Zipf plot is a well-known visual representation of the distribution of frequencies, but for the current problem, we’ll switch to a different representation.
Tail DistributionGiven the number of times each word appear in the corpus, we can compute the rates, which is the number of times we expect each word to appear in a sample of a given size, and the inverse rates, which are the number of words we need to see before we expect a given word to appear.
We will find it most convenient to work with the distribution of inverse rates on a log scale. The first step is to use the observed frequencies to estimate word rates – we’ll estimate the rate at which each word would appear in a random sample.
We’ll do that by creating a beta distribution that represents the posterior distribution of word rates, given the observed frequencies (see this section of Think Bayes) – and then drawing a random sample from the posterior. So words that have the same frequency will not generally have the same inferred rate.
from scipy.stats import betanp.random.seed(17)alphas = freqs + 1betas = num_words - freqs + 1inferred_rates = beta(alphas, betas).rvs()Now we can compute the inverse rates, which are the number of words we have to sample before we expect to see each word once.
inverse_rates = 1 / inferred_ratesAnd here are their magnitudes, expressed as logarithms base 10.
mags = np.log10(inverse_rates)To represent the distribution of these magnitudes, we’ll use a Surv object, which represents survival functions, but we’ll use a variation of the survival function which is the probability that a randomly-chosen value is greater than or equal to a given quantity. The following function computes this version of a survival function, which is called a tail probability.
from empiricaldist import Survdef make_surv(seq): """Make a non-standard survival function, P(X>=x)""" pmf = Pmf.from_seq(seq) surv = pmf.make_surv() + pmf # correct for numerical error surv.iloc[0] = 1 return Surv(surv)Here’s how we make the survival function.
surv = make_surv(mags)And here’s what it looks like.
options = dict(marker=".", ms=2, lw=0.5, label="data")surv.plot(**options)decorate(xlabel="Inverse rate (log10 words per appearance)", ylabel="Tail probability")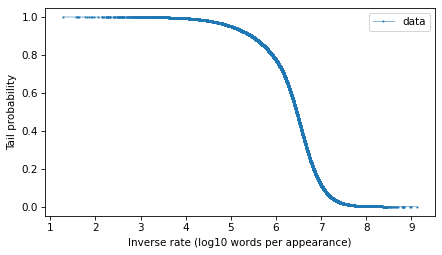
The tail distribution has the sigmoid shape that is characteristic of normal distributions and t distributions, although it is notably asymmetric.
And here’s what the tail probabilities look like on a log-y scale.
surv.plot(**options)decorate(xlabel="Inverse rate (words per appearance)", yscale="log")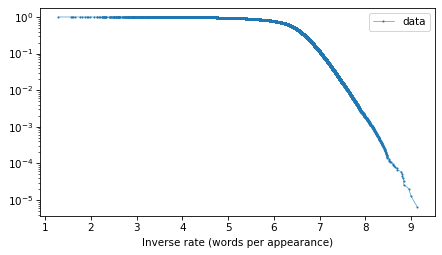
If this distribution were normal, we would expect this curve to drop off with increasing slope. But for the words with the lowest frequencies – that is, the highest inverse rates – it is almost a straight line. And that suggests that a
distribution might be a good model for this data.
Fitting a ModelTo estimate the frequency of rare words, we will need to model the tail behavior of this distribution and extrapolate it beyond the data. So let’s fit a t distribution and see how it looks. I’ll use code from Chapter 8 of Probably Overthinking It, which is all about these long-tailed distributions.
The following function makes a Surv object that represents a t distribution with the given parameters.
from scipy.stats import t as t_distdef truncated_t_sf(qs, df, mu, sigma): """Makes Surv object for a t distribution. Truncated on the left, assuming all values are greater than min(qs) """ ps = t_dist.sf(qs, df, mu, sigma) surv_model = Surv(ps / ps[0], qs) return surv_modelIf we are given the df parameter, we can use the following function to find the values of mu and sigma that best fit the data, focusing on the central part of the distribution.
from scipy.optimize import least_squaresdef fit_truncated_t(df, surv): """Given df, find the best values of mu and sigma.""" low, high = surv.qs.min(), surv.qs.max() qs_model = np.linspace(low, high, 2000) ps = np.linspace(0.1, 0.8, 20) qs = surv.inverse(ps) def error_func_t(params, df, surv): mu, sigma = params surv_model = truncated_t_sf(qs_model, df, mu, sigma) error = surv(qs) - surv_model(qs) return error pmf = surv.make_pmf() pmf.normalize() params = pmf.mean(), pmf.std() res = least_squares(error_func_t, x0=params, args=(df, surv), xtol=1e-3) assert res.success return res.xBut since we are not given df, we can use the following function to search for the value that best fits the tail of the distribution.
from scipy.optimize import minimizedef minimize_df(df0, surv, bounds=[(1, 1e3)], ps=None):
low, high = surv.qs.min(), surv.qs.max()
qs_model = np.linspace(low, high * 1.2, 2000)
if ps is None:
t = surv.ps[0], surv.ps[-5]
low, high = np.log10(t)
ps = np.logspace(low, high, 30, endpoint=False)
qs = surv.inverse(ps)
def error_func_tail(params):
(df,) = params
# print(df)
mu, sigma = fit_truncated_t(df, surv)
surv_model = truncated_t_sf(qs_model, df, mu, sigma)
errors = np.log10(surv(qs)) - np.log10(surv_model(qs))
return np.sum(errors**2)
params = (df0,)
res = minimize(error_func_tail, x0=params, bounds=bounds, method="Powell")
assert res.success
return res.x
df = minimize_df(25, surv)dfarray([22.52401171])mu, sigma = fit_truncated_t(df, surv)df, mu, sigma(array([22.52401171]), 6.433323515095857, 0.49070837962997577)
Here’s the t distribution that best fits the data.
low, high = surv.qs.min(), surv.qs.max()qs = np.linspace(low, 10, 2000)surv_model = truncated_t_sf(qs, df, mu, sigma)surv_model.plot(color="gray", alpha=0.4, label="model")surv.plot(**options)decorate(xlabel="Inverse rate (log10 words per appearance)", ylabel="Tail probability")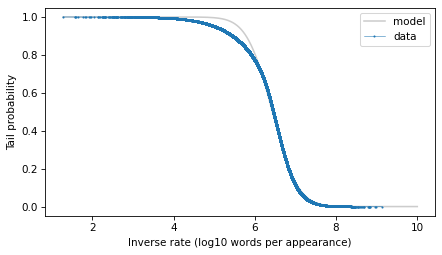
With the y-axis on a linear scale, we can see that the model fits the data reasonably well, except for a range between 5 and 6 – that is for words that appear about 1 time in a million.
Here’s what the model looks like on a log-y scale.
surv_model.plot(color="gray", alpha=0.4, label="model")surv.plot(**options)decorate( xlabel="Inverse rate (log10 words per appearance)", ylabel="Tail probability", yscale="log",)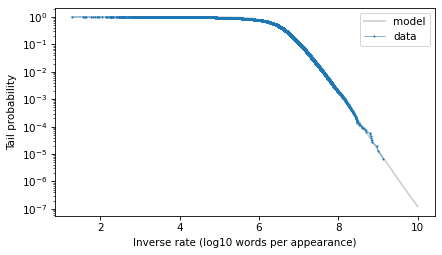
The model fits the data well in the extreme tail, which is exactly where we need it. And we can use the model to extrapolate a little beyond the data, to make sure we cover the range that will turn out to be likely in the scenario where we hear a word for this first time after 50 years.
The UpdateThe model we’ve developed is the distribution of inverse rates for the words that appear in the corpus and, by extrapolation, for additional rare words that didn’t appear in the corpus. This distribution will be the prior for the Bayesian update. We just have to convert it from a survival function to a PMF (remembering that these are equivalent representations of the same distribution).
prior = surv_model.make_pmf()prior.plot(label="prior")decorate( xlabel="Inverse rate (log10 words per appearance)", ylabel="Density",)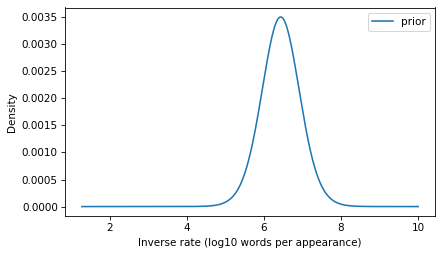
To compute the likelihood of the observation, we have to transform the inverse rates to probabilities.
ps = 1 / np.power(10, prior.qs)Now suppose that in a given day, you read or hear 10,000 words in a context where you would notice if you heard a word for the first time. Here’s the number of words you would hear in 50 years.
words_per_day = 10_000days = 50 * 365k = days * words_per_dayk182500000Now, what’s the probability that you fail to encounter a word in k attempts and then encounter it on the next attempt? We can answer that with the negative binomial distribution, which computes the probability of getting the nth success after k failures, for a given probability – or in this case, for a sequence of possible probabilities.
from scipy.stats import nbinomn = 1likelihood = nbinom.pmf(k, n, ps)With this likelihood and the prior, we can compute the posterior distribution in the usual way.
posterior = prior * likelihoodposterior.normalize()1.368245917258196e-11And here’s what it looks like.
prior.plot(alpha=0.5, label="prior")posterior.plot(label="posterior")decorate( xlabel="Inverse rate (log10 words per appearance)", ylabel="Density",)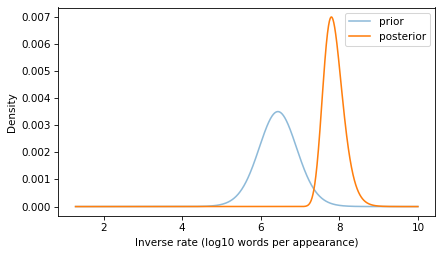
If you go 50 years without hearing a word, that suggests that it is a rare word, and the posterior distribution reflects that logic.
The posterior distribution represents a range of possible values for the inverse rate of the word you heard. Now we can use it to answer the question we started with: what is the probability of hearing the same word again on the same day – that is, within the next 10,000 words you hear?
To answer that, we can use the survival function of the binomial distribution to compute the probability of more than 0 successes in the next n_pred attempts. We’ll compute this probability for each of the ps that correspond to the inverse rates in the posterior.
from scipy.stats import binomn_pred = words_per_dayps_pred = binom.sf(0, n_pred, ps)And we can use the probabilities in the posterior to compute the expected value – by the law of total probability, the result is the probability of hearing the same word again within a day.
p = np.sum(posterior * ps_pred)p, 1 / p(0.00016019406802217392, 6242.42840166579)The result is about 1 in 6000.
With all of the assumptions we made in this calculation, there’s no reason to be more precise than that. And as I mentioned at the beginning, we should probably not take this conclusion to seriously. If you hear a word for the first time after 50 years, there’s a good chance the word is “having a moment”, which greatly increases the chance you’ll hear it again. I can’t think of why chartism might be in the news at the moment, but maybe this post will go viral and make it happen.
November 17, 2024
Comparing Distributions
This is the second is a series of excerpts from Elements of Data Science which available from Lulu.com and online booksellers. It’s from Chapter 8, which is about representing distribution using PMFs and CDFs. This section explains why I think CDFs are often better for plotting and comparing distributions.You can read the complete chapter here, or run the Jupyter notebook on Colab.
So far we’ve seen two ways to represent distributions, PMFs and CDFs. Now we’ll use PMFs and CDFs to compare distributions, and we’ll see the pros and cons of each. One way to compare distributions is to plot multiple PMFs on the same axes. For example, suppose we want to compare the distribution of age for male and female respondents. First we’ll create a Boolean Series that’s true for male respondents and another that’s true for female respondents.
male = (gss['sex'] == 1)female = (gss['sex'] == 2)We can use these Series to select ages for male and female respondents.
male_age = age[male]female_age = age[female]And plot a PMF for each.
pmf_male_age = Pmf.from_seq(male_age)pmf_male_age.plot(label='Male')pmf_female_age = Pmf.from_seq(female_age)pmf_female_age.plot(label='Female')plt.xlabel('Age (years)') plt.ylabel('PMF')plt.title('Distribution of age by sex')plt.legend();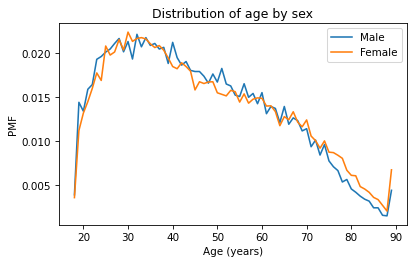
A plot as variable as this is often described as noisy. If we ignore the noise, it looks like the PMF is higher for men between ages 40 and 50, and higher for women between ages 70 and 80. But both of those differences might be due to randomness.
Now let’s do the same thing with CDFs – everything is the same except we replace Pmf with Cdf.
cdf_male_age = Cdf.from_seq(male_age)cdf_male_age.plot(label='Male')cdf_female_age = Cdf.from_seq(female_age)cdf_female_age.plot(label='Female')plt.xlabel('Age (years)') plt.ylabel('CDF')plt.title('Distribution of age by sex')plt.legend();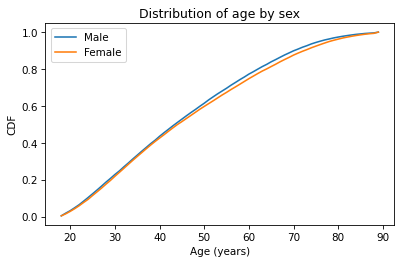
Because CDFs smooth out randomness, they provide a better view of real differences between distributions. In this case, the lines are close together until age 40 – after that, the CDF is higher for men than women.
So what does that mean? One way to interpret the difference is that the fraction of men below a given age is generally more than the fraction of women below the same age. For example, about 77% of men are 60 or less, compared to 75% of women.
cdf_male_age(60), cdf_female_age(60)(array(0.7721998), array(0.7474241))Going the other way, we could also compare percentiles. For example, the median age woman is older than the median age man, by about one year.
cdf_male_age.inverse(0.5), cdf_female_age.inverse(0.5)(array(44.), array(45.))Comparing IncomesAs another example, let’s look at household income and compare the distribution before and after 1995 (I chose 1995 because it’s roughly the midpoint of the survey). We’ll make two Boolean Series objects to select respondents interviewed before and after 1995.
pre95 = (gss['year'] < 1995)post95 = (gss['year'] >= 1995)Now we can plot the PMFs of realinc, which records household income converted to 1986 dollars.
realinc = gss['realinc']Pmf.from_seq(realinc[pre95]).plot(label='Before 1995')Pmf.from_seq(realinc[post95]).plot(label='After 1995')plt.xlabel('Income (1986 USD)')plt.ylabel('PMF')plt.title('Distribution of income')plt.legend();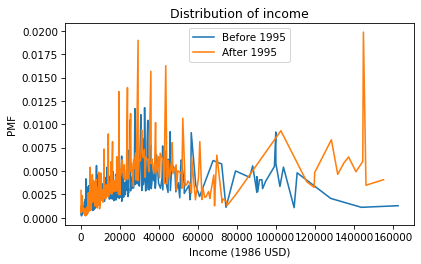
There are a lot of unique values in this distribution, and none of them appear very often. As a result, the PMF is so noisy and we can’t really see the shape of the distribution. It’s also hard to compare the distributions. It looks like there are more people with high incomes after 1995, but it’s hard to tell. We can get a clearer picture with a CDF.
Cdf.from_seq(realinc[pre95]).plot(label='Before 1995')Cdf.from_seq(realinc[post95]).plot(label='After 1995')plt.xlabel('Income (1986 USD)')plt.ylabel('CDF')plt.title('Distribution of income')plt.legend();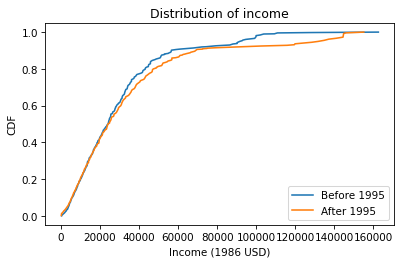
Below $30,000 the CDFs are almost identical; above that, we can see that the post-1995 distribution is shifted to the right. In other words, the fraction of people with high incomes is about the same, but the income of high earners has increased.
In general, I recommend CDFs for exploratory analysis. They give you a clear view of the distribution, without too much noise, and they are good for comparing distributions.
November 10, 2024
War and Peace and Zipf’s Law
Elements of Data Science is in print now, available from Lulu.com and online booksellers. To celebrate, I’ll post some excerpts here, starting with one of my favorite examples, Zipf’s Law. It’s from Chapter 6, which is about plotting data, and it uses Python dictionaries, which are covered in the previous chapter. You can read the complete chapter here, or run the Jupyter notebook on Colab.
In almost any book, in almost any language, if you count the number of unique words and the number of times each word appears, you will find a remarkable pattern: the most common word appears twice as often as the second most common – at least approximately – three times as often as the third most common, and so on.
In general, if we sort the words in descending order of frequency, there is an inverse relationship between the rank of the words – first, second, third, etc. – and the number of times they appear. This observation was most famously made by George Kingsley Zipf, so it is called Zipf’s law.
To see if this law holds for the words in War and Peace, we’ll make a Zipf plot, which shows:
The frequency of each word on the y-axis, andThe rank of each word on the x-axis, starting from 1.In the previous chapter, we looped through the book and made a string that contains all punctuation characters. Here are the results, which we will need again.
all_punctuation = ',.-:[#]*/“’—‘!?”;()%@'The following program reads through the book and makes a dictionary that maps from each word to the number of times it appears.
fp = open('2600-0.txt')for line in fp: if line.startswith('***'): breakunique_words = {}for line in fp: if line.startswith('***'): break for word in line.split(): word = word.lower() word = word.strip(all_punctuation) if word in unique_words: unique_words[word] = 1 else: unique_words[word] = 1In unique_words, the keys are words and the values are their frequencies. We can use the values function to get the values from the dictionary. The result has the type dict_values:
freqs = unique_words.values()type(freqs)dict_valuesBefore we plot them, we have to sort them, but the sort function doesn’t work with dict_values.
%%expect AttributeErrorfreqs.sort()AttributeError: 'dict_values' object has no attribute 'sort'We can use list to make a list of frequencies:
freq_list = list(unique_words.values())type(freq_list)listAnd now we can use sort. By default it sorts in ascending order, but we can pass a keyword argument to reverse the order.
freq_list.sort(reverse=True)Now, for the ranks, we need a sequence that counts from 1 to n, where n is the number of elements in freq_list. We can use the range function, which returns a value with type range. As a small example, here’s the range from 1 to 5.
range(1, 5)range(1, 5)However, there’s a catch. If we use the range to make a list, we see that “the range from 1 to 5” includes 1, but it doesn’t include 5.
list(range(1, 5))[1, 2, 3, 4]That might seem strange, but it is often more convenient to use range when it is defined this way, rather than what might seem like the more natural way. Anyway, we can get what we want by increasing the second argument by one:
list(range(1, 6))[1, 2, 3, 4, 5]So, finally, we can make a range that represents the ranks from 1 to n:
n = len(freq_list)ranks = range(1, n 1)ranksrange(1, 20484)And now we can plot the frequencies versus the ranks:
plt.plot(ranks, freq_list)plt.xlabel('Rank')
plt.ylabel('Frequency')
plt.title("War and Peace and Zipf's law");
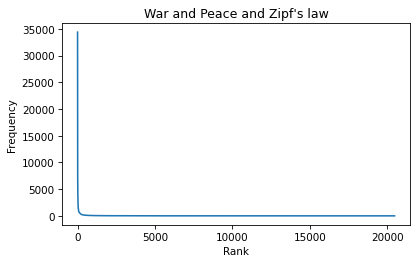
According to Zipf’s law, these frequencies should be inversely proportional to the ranks. If that’s true, we can write:
f = k / r
where r is the rank of a word, f is its frequency, and k is an unknown constant of proportionality. If we take the logarithm of both sides, we get
log f = log k – log r
This equation implies that if we plot f versus r on a log-log scale, we expect to see a straight line with intercept at log k and slope -1.
6.6. Logarithmic ScalesWe can use plt.xscale to plot the x-axis on a log scale.
plt.plot(ranks, freq_list)plt.xlabel('Rank')plt.ylabel('Frequency')plt.title("War and Peace and Zipf's law")plt.xscale('log')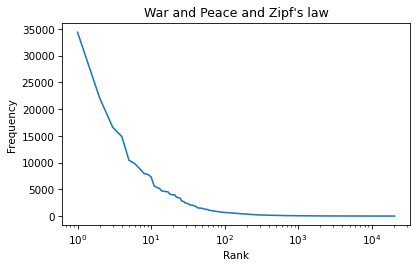
And plt.yscale to plot the y-axis on a log scale.
plt.plot(ranks, freq_list)plt.xlabel('Rank')plt.ylabel('Frequency')plt.title("War and Peace and Zipf's law")plt.xscale('log')plt.yscale('log')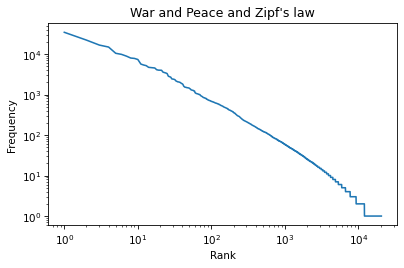
The result is not quite a straight line, but it is close. We can get a sense of the slope by connecting the end points with a line. First, we’ll select the first and last elements from xs.
xs = ranks[0], ranks[-1]xs(1, 20483)And the first and last elements from ys.
ys = freq_list[0], freq_list[-1]ys(34389, 1)And plot a line between them.
plt.plot(xs, ys, color='gray')plt.plot(ranks, freq_list)plt.xlabel('Rank')plt.ylabel('Frequency')plt.title("War and Peace and Zipf's law")plt.xscale('log')plt.yscale('log')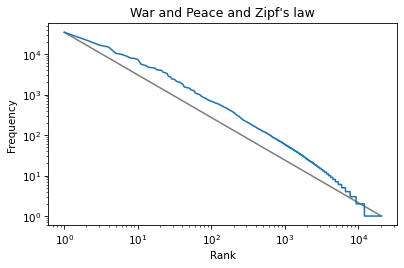
The slope of this line is the “rise over run”, that is, the difference on the y-axis divided by the difference on the x-axis. We can compute the rise using np.log10 to compute the log base 10 of the first and last values:
np.log10(ys)array([4.53641955, 0. ])Then we can use np.diff to compute the difference between the elements:
rise = np.diff(np.log10(ys))risearray([-4.53641955])Exercise: Use log10 and diff to compute the run, that is, the difference on the x-axis. Then divide the rise by the run to get the slope of the grey line. Is it close to -1, as Zipf’s law predicts? Hint: yes.
Zipf’s Law
Elements of Data Science is in print now, available from Lulu.com and online booksellers. To celebrate, I’ll post some excerpts here, starting with one of my favorite examples, Zipf’s Law. You can read the complete chapter here, or run the Jupyter notebook on Colab.
In almost any book, in almost any language, if you count the number of unique words and the number of times each word appears, you will find a remarkable pattern: the most common word appears twice as often as the second most common – at least approximately – three times as often as the third most common, and so on.
In general, if we sort the words in descending order of frequency, there is an inverse relationship between the rank of the words – first, second, third, etc. – and the number of times they appear. This observation was most famously made by George Kingsley Zipf, so it is called Zipf’s law.
To see if this law holds for the words in War and Peace, we’ll make a Zipf plot, which shows:
The frequency of each word on the y-axis, andThe rank of each word on the x-axis, starting from 1.In the previous chapter, we looped through the book and made a string that contains all punctuation characters. Here are the results, which we will need again.
all_punctuation = ',.-:[#]*/“’—‘!?”;()%@'The following program reads through the book and makes a dictionary that maps from each word to the number of times it appears.
fp = open('2600-0.txt')for line in fp: if line.startswith('***'): breakunique_words = {}for line in fp: if line.startswith('***'): break for word in line.split(): word = word.lower() word = word.strip(all_punctuation) if word in unique_words: unique_words[word] = 1 else: unique_words[word] = 1In unique_words, the keys are words and the values are their frequencies. We can use the values function to get the values from the dictionary. The result has the type dict_values:
freqs = unique_words.values()type(freqs)dict_valuesBefore we plot them, we have to sort them, but the sort function doesn’t work with dict_values.
%%expect AttributeErrorfreqs.sort()AttributeError: 'dict_values' object has no attribute 'sort'We can use list to make a list of frequencies:
freq_list = list(unique_words.values())type(freq_list)listAnd now we can use sort. By default it sorts in ascending order, but we can pass a keyword argument to reverse the order.
freq_list.sort(reverse=True)Now, for the ranks, we need a sequence that counts from 1 to n, where n is the number of elements in freq_list. We can use the range function, which returns a value with type range. As a small example, here’s the range from 1 to 5.
range(1, 5)range(1, 5)However, there’s a catch. If we use the range to make a list, we see that “the range from 1 to 5” includes 1, but it doesn’t include 5.
list(range(1, 5))[1, 2, 3, 4]That might seem strange, but it is often more convenient to use range when it is defined this way, rather than what might seem like the more natural way. Anyway, we can get what we want by increasing the second argument by one:
list(range(1, 6))[1, 2, 3, 4, 5]So, finally, we can make a range that represents the ranks from 1 to n:
n = len(freq_list)ranks = range(1, n 1)ranksrange(1, 20484)And now we can plot the frequencies versus the ranks:
plt.plot(ranks, freq_list)plt.xlabel('Rank')
plt.ylabel('Frequency')
plt.title("War and Peace and Zipf's law");

According to Zipf’s law, these frequencies should be inversely proportional to the ranks. If that’s true, we can write:
f = k / r
where r is the rank of a word, f is its frequency, and k is an unknown constant of proportionality. If we take the logarithm of both sides, we get
log f = log k – log r
This equation implies that if we plot f versus r on a log-log scale, we expect to see a straight line with intercept at log k and slope -1.
6.6. Logarithmic ScalesWe can use plt.xscale to plot the x-axis on a log scale.
plt.plot(ranks, freq_list)plt.xlabel('Rank')plt.ylabel('Frequency')plt.title("War and Peace and Zipf's law")plt.xscale('log')
And plt.yscale to plot the y-axis on a log scale.
plt.plot(ranks, freq_list)plt.xlabel('Rank')plt.ylabel('Frequency')plt.title("War and Peace and Zipf's law")plt.xscale('log')plt.yscale('log')
The result is not quite a straight line, but it is close. We can get a sense of the slope by connecting the end points with a line. First, we’ll select the first and last elements from xs.
xs = ranks[0], ranks[-1]xs(1, 20483)And the first and last elements from ys.
ys = freq_list[0], freq_list[-1]ys(34389, 1)And plot a line between them.
plt.plot(xs, ys, color='gray')plt.plot(ranks, freq_list)plt.xlabel('Rank')plt.ylabel('Frequency')plt.title("War and Peace and Zipf's law")plt.xscale('log')plt.yscale('log')
The slope of this line is the “rise over run”, that is, the difference on the y-axis divided by the difference on the x-axis. We can compute the rise using np.log10 to compute the log base 10 of the first and last values:
np.log10(ys)array([4.53641955, 0. ])Then we can use np.diff to compute the difference between the elements:
rise = np.diff(np.log10(ys))risearray([-4.53641955])Exercise: Use log10 and diff to compute the run, that is, the difference on the x-axis. Then divide the rise by the run to get the slope of the grey line. Is it close to -1, as Zipf’s law predicts? Hint: yes.
October 22, 2024
Think Stats 3rd Edition
I am excited to announce that I have started work on a third edition of Think Stats, to be published by O’Reilly Media in 2025. At this point the content is mostly settled, and I am revising chapters to get them ready for technical review.
If you want to start reading now, the current draft is here.
What’s new?For the third edition, I started by moving the book into Jupyter notebooks. This change has one immediate benefit – you can read the text, run the code, and work on the exercises all in one place. And the notebooks are designed to work on Google Colab, so you can get started without installing anything.
The move to notebooks has another benefit – the code is more visible. In the first two editions, some of the code was in the book and some was in supporting files available online. In retrospect, it’s clear that splitting the material in this way was not ideal, and it made the code more complicated than it needed to be. In the third edition, I was able to simplify the code and make it more readable.
Since the last edition was published, I’ve developed a library called empiricaldist that provides objects that represent statistical distributions. This library is more mature now, so the updated code makes better use of it.
When I started this project, NumPy and SciPy were not as widely used, and Pandas even less, so the original code used Python data structures like lists and dictionaries. This edition uses arrays and Pandas structures extensively, and makes more use of functions these libraries provide. I assume readers have some familiarity with these tools, but I explain each feature when it first appears.
The third edition covers the same topics as the original, in almost the same order, but the text is substantially revised. Some of the examples are new; others are updated with new data. I’ve developed new exercises, revised some of the old ones, and removed a few. I think the updated exercises are better connected to the examples, and more interesting.
Since the first edition, this book has been based on the thesis that many ideas that are hard to explain with math are easier to explain with code. In this edition, I have doubled down on this idea, to the point where there is almost no mathematical notation, only code.
Overall, I think these changes make Think Stats a better book. To give you a taste, here’s an excerpt from Chapter 12: Time Series Analysis.
Multiplicative ModelThe additive model we used in the previous section is based on the assumption that the time series is well modeled as the sum of a long-term trend, a seasonal component, and a residual component – which implies that the magnitude of the seasonal component and the residuals does not vary over time.
As an example that violates this assumption, let’s look at small-scale solar electricity production since 2014.
solar = elec["United States : small-scale solar photovoltaic"].dropna()solar.plot(label="solar")decorate(ylabel="GWh")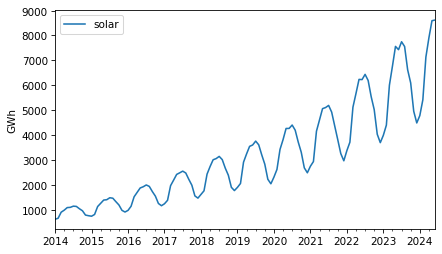
Over this interval, total production has increased several times over. And it’s clear that the magnitude of seasonal variation has increased as well.
If suppose that the magnitudes of seasonal and random variation are proportional to the magnitude of the trend, that suggests an alternative to the additive model in which the time series is the product of a trend, a seasonal component, and a residual component.
To try out this multiplicative model, we’ll split this series into training and test sets.
training, test = split_series(solar)And call seasonal_decompose with the model=multiplicative argument.
decomposition = seasonal_decompose(training, model="multiplicative", period=12)Here’s what the results look like.
plot_decomposition(training, decomposition)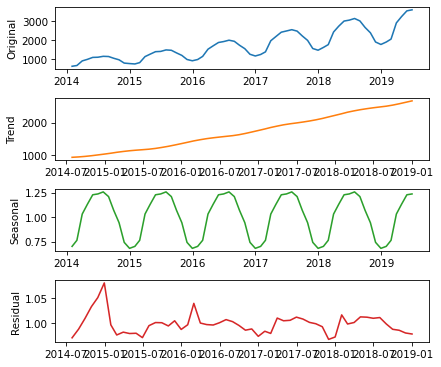
Now the seasonal and residual components are multiplicative factors. So, it looks like the seasonal component varies from about 25% below the trend to 25% above. And the residual component is usually less than 5% either way, with the exception of some larger factors in the first period.
trend = decomposition.trendseasonal = decomposition.seasonalresid = decomposition.residThe R² value of this model is very high.
rsquared = 1 - resid.var() / training.var()rsquared0.9999999992978134The production of a solar panel is almost entirely a function of the sunlight it’s exposed to, so it makes sense that it follows an annual cycle so closely.
To predict the long term trend, we’ll use a quadratic model.
months = range(len(training))data = pd.DataFrame({"trend": trend, "months": months}).dropna()results = smf.ols("trend ~ months + I(months**2)", data=data).fit()In the Patsy formula, the term "I(months**2)" adds a quadratic term to the model, so we don’t have to compute it explicitly. Here are the results.
display_summary(results)coefstd errtP>|t|[0.0250.975]Intercept766.196213.49456.7820.000739.106793.286months22.21530.93823.6730.00020.33124.099I(months ** 2)0.17620.01412.4800.0000.1480.205R-squared:0.9983The p-values of the linear and quadratic terms are very low, which suggests that the quadratic model captures more information about the trend than a linear model would – and the R² value is very high.
Now we can use the model to compute the expected value of the trend for the past and future.
months = range(len(solar))df = pd.DataFrame({"months": months})pred_trend = results.predict(df)pred_trend.index = solar.indexHere’s what it looks like.
pred_trend.plot(color="0.8", label="quadratic model")trend.plot(color="C1")decorate(ylabel="GWh")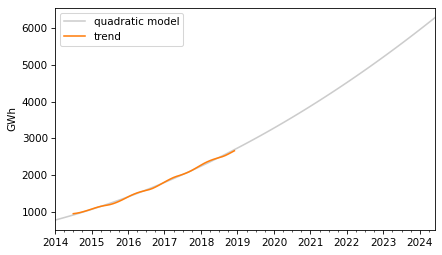
The quadratic model fits the past trend well. Now we can use the seasonal component from the decomposition to predict the seasonal component.
monthly_averages = seasonal.groupby(seasonal.index.month).mean()pred_seasonal = monthly_averages[pred_trend.index.month]pred_seasonal.index = pred_trend.indexFinally, to compute “retrodictions” for past values and predictions for the future, we multiply the trend and the seasonal component.
pred = pred_trend * pred_seasonalHere is the result along with the training data.
training.plot(label="training")pred.plot(alpha=0.6, color="0.6", label="prediction")decorate(ylabel="GWh")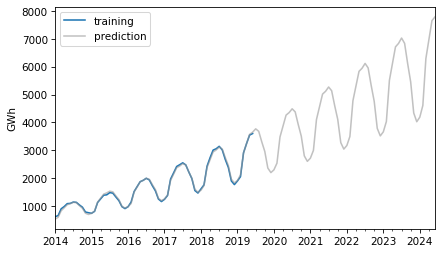
The retrodictions fit the training data well and the predictions seem plausible – now let’s see if they turned out to be accurate. Here are the predictions along with the test data.
future = pred[test.index]future.plot(ls="--", color="0.6", label="prediction")test.plot(label="actual")decorate(ylabel="GWh")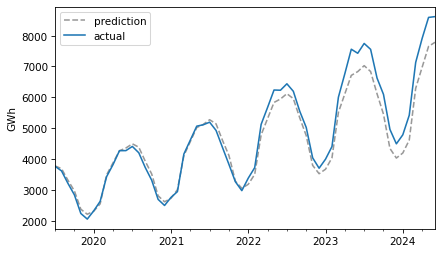
For the first three years, the predictions are very good. After that, it looks like actual growth exceeded expectations.
In this example, seasonal decomposition worked well for modeling and predicting solar production, but in the previous example, it was not very effective for nuclear production. In the next section, we’ll try a different approach, autoregression.
October 15, 2024
Bootstrapping a Proportion
It’s another installment in Data Q&A: Answering the real questions with Python. Previous installments are available from the Data Q&A landing page.
Here’s a question from the Reddit statistics forum.
How do I use bootstrapping to generate confidence intervals for a proportion/ratio? The situation is this:
I obtain samples of text with differing numbers of lines. From several tens to over a million. I have no control over how many lines there are in any given sample. Each line of each sample may or may not contain a string S. Counting lines according to S presence or S absence generates a ratio of S to S’ for that sample. I want to use bootstrapping to calculate confidence intervals for the found ratio (which of course will vary with sample size).
To do this I could either:
A. Literally resample (10,000 times) of size (say) 1,000 from the original sample (with replacement) then categorise S (and S’), and then calculate the ratio for each resample, and finally identify highest and lowest 2.5% (for 95% CI), or
B. Generate 10,000 samples of 1,000 random numbers between 0 and 1, scoring each stochastically as above or below original sample ratio (equivalent to S or S’). Then calculate CI as in A.
Programmatically A is slow and B is very fast. Is there anything wrong with doing B? The confidence intervals generated by each are almost identical.
The answer to the immediate question is that A and B are equivalent, so there’s nothing wrong with B. But in follow-up responses, a few related questions were raised:
Is resampling a good choice for this problem?What size should the resamplings be?How many resamplings do we need?I don’t think resampling is really necessary here, and I’ll show some alternatives. And I’ll answer the other questions along the way.
Click here to run this notebook on Colab.
I’ll download a utilities module with some of my frequently-used functions, and then import the usual libraries.
Pallor and ProbabilityAs an example, let’s use one of the exercises from Think Python:
The Count of Monte Cristo is a novel by Alexandre Dumas that is considered a classic. Nevertheless, in the introduction of an English translation of the book, the writer Umberto Eco confesses that he found the book to be “one of the most badly written novels of all time”.
In particular, he says it is “shameless in its repetition of the same adjective,” and mentions in particular the number of times “its characters either shudder or turn pale.”
To see whether his objection is valid, let’s count the number number of lines that contain the word pale in any form, including pale, pales, paled, and paleness, as well as the related word pallor. Use a single regular expression that matches all of these words and no others.
The following cell downloads the text of the book from Project Gutenberg.
download('https://www.gutenberg.org/cache/epub/...We’ll use the following functions to remove the additional material that appears before and after the text of the book.
def is_special_line(line): return line.startswith('*** ')def clean_file(input_file, output_file): reader = open(input_file) writer = open(output_file, 'w') for line in reader: if is_special_line(line): break for line in reader: if is_special_line(line): break writer.write(line) reader.close() writer.close()clean_file('pg1184.txt', 'pg1184_cleaned.txt')And we’ll use the following function to count the number of lines that contain a particular pattern of characters.
import redef count_matches(lines, pattern): count = 0 for line in lines: result = re.search(pattern, line) if result: count = 1 return countreadlines reads the file and creates a list of strings, one for each line.
lines = open('pg1184_cleaned.txt').readlines()n = len(lines)n61310There are about 61,000 lines in the file.
The following pattern matches “pale” and several related words.
pattern = r'\b(pale|pales|paled|paleness|pallor)\b'k = count_matches(lines, pattern)k223These words appear in 223 lines of the file.
p_est = k / np_est0.0036372533028869677So the estimated proportion is about 0.0036. To quantify the precision of that estimate, we’ll compute a confidence interval.
ResamplingFirst we’ll use the method OP called A – literally resampling the lines of the file. The following function takes a list of lines and selects a sample, with replacement, that has the same size.
def resample(lines): return np.random.choice(lines, len(lines), replace=True)In a resampled list, the same line can appear more than once, and some lines might not appear at all. So in any resampling, the forbidden words might appear more times than in the original text, or fewer. Here’s an example.
np.random.seed(1)count_matches(resample(lines), pattern)201In this resampling, the words appear in 201 lines, fewer than in the original (223).
If we repeat this process many times, we can compute a sample of possible values of k. Because this method is slow, we’ll only repeat it 101 times.
ks_resampling = [count_matches(resample(lines), pattern) for i in range(101)]With these different values of k, we can divide by n to get the corresponding values of p.
ps_resampling = np.array(ks_resampling) / nTo see what the distribution of those values looks like, we’ll plot the CDF.
from empiricaldist import CdfCdf.from_seq(ps_resampling).plot(label='resampling')decorate(xlabel='Resampled proportion', ylabel='Density')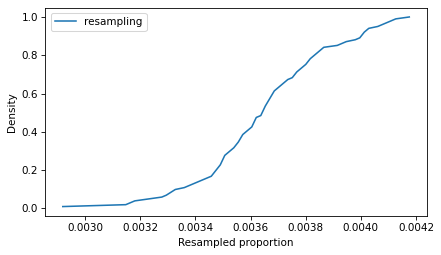
So that’s the slow way to compute the sampling distribution of the proportion. The method OP calls B is to simulate a Bernoulli trial with size n and probability of success p_est. One way to do that is to draw random numbers from 0 to 1 and count how many are less than p_est.
(np.random.random(n) < p_est).sum()229Equivalently, we can draw a sample from a Bernoulli distribution and add it up.
from scipy.stats import bernoullibernoulli(p_est).rvs(n).sum()232These values follow a binomial distribution with parameters n and p_est. So we can simulate a large number of trials quickly by drawing values from a binomial distribution.
from scipy.stats import binomks_binom = binom(n, p_est).rvs(10001)Dividing by n, we can compute the corresponding sample of proportions.
ps_binom = np.array(ks_binom) / nBecause this method is so much faster, we can generate a large number of values, which means we get a more precise picture of the sampling distribution.
The following figure compares the CDFs of the values we got by resampling and the values we got from the binomial distribution.
Cdf.from_seq(ps_resampling).plot(label='resampling')Cdf.from_seq(ps_binom).plot(label='binomial')decorate(xlabel='Resampled proportion', ylabel='CDF')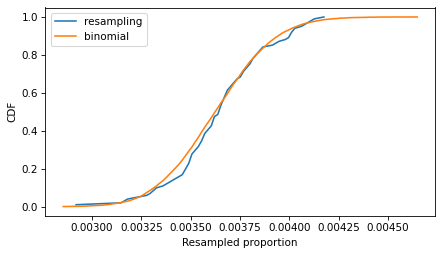
If we run the resampling method longer, these CDFs converge, so the two methods are equivalent.
To compute a 90% confidence interval, we can use the values we sampled from the binomial distribution.
np.percentile(ps_binom, [5, 95])array([0.0032458 , 0.00404502])Or we can use the inverse CDF of the binomial distribution, which is even faster than drawing a sample. And it’s deterministic – that is, we get the same result every time, with no randomness.
binom(n, p_est).ppf([0.05, 0.95]) / narray([0.0032458 , 0.00404502])Using the inverse CDF of the binomial distribution is a good way to compute confidence intervals. But before we get to that, let’s see how resampling behaves as we increase the sample size and the number of iterations.
Sample SizeIn the example, the sample size is more than 60,000, so the CI is very small. The following figure shows what it looks like for more moderate sample sizes, using p=0.1 as an example.
p = 0.1ns = [50, 500, 5000]ci_df = pd.DataFrame(index=ns, columns=['low', 'high'])for n in ns: ks = binom(n, p).rvs(10001) ps = ks / n Cdf.from_seq(ps).plot(label=f"n = {n}") ci_df.loc[n] = np.percentile(ps, [5, 95]) decorate(xlabel='Proportion', ylabel='CDF')
As the sample size increases, the spread of the sampling distribution gets smaller, and so does the width of the confidence interval.
ci_df['width'] = ci_df['high'] - ci_df['low']ci_dflowhighwidth500.040.180.145000.0780.1220.04450000.09320.10720.014With resampling methods, it is important to draw samples with the same size as the original dataset – otherwise the result is wrong.
But the number of iterations doesn’t matter as much. The following figure shows the sampling distribution if we run the sampling process 101, 1001, and 10,001 times.
p = 0.1n = 100iter_seq = [101, 1001, 100001]for iters in iter_seq: ks = binom(n, p).rvs(iters) ps = ks / n Cdf.from_seq(ps).plot(label=f"iters = {iters}") decorate()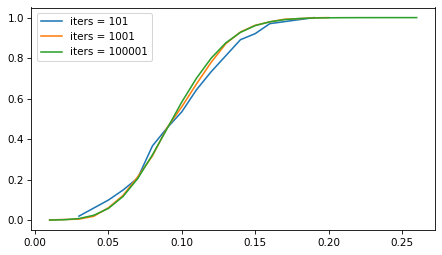
The sampling distribution is the same, regardless of how many iterations we run. But with more iterations, we get a better picture of the distribution and a more precise estimate of the confidence interval. For most problems, 1001 iterations is enough, but if you can generate larger samples fast enough, more is better.
However, for this problem, resampling isn’t really necessary. As we’ve seen, we can use the binomial distribution to compute a CI without drawing a random sample at all. And for this problem, there are approximations that are even easier to compute – although they come with some caveats.
ApproximationsIf n is large and p is not too close to 0 or 1, the sampling distribution of a proportion is well modeled by a normal distribution, and we can approximate a confidence interval with just a few calculations.
For a given confidence level, we can use the inverse CDF of the normal distribution to compute a
score, which is the number of standard deviations the CI should span – above and below the observed value of p – in order to include the given confidence.
from scipy.stats import normconfidence = 0.9z = norm.ppf(1 - (1 - confidence) / 2)z1.6448536269514722A 90% confidence interval spans about 1.64 standard deviations.
Now we can use the following function, which uses p, n, and this z score to compute the confidence interval.
def confidence_interval_normal_approx(k, n, z): p = k / n margin_of_error = z * np.sqrt(p * (1 - p) / n) lower_bound = p - margin_of_error upper_bound = p margin_of_error return lower_bound, upper_boundTo test it, we’ll compute n and k for the example again.
n = len(lines)k = count_matches(lines, pattern)n, k(61310, 223)Here’s the confidence interval based on the normal approximation.
ci_normal = confidence_interval_normal_approx(k, n, z)ci_normal(0.003237348046298746, 0.00403715855947519)In the example, n is large, which is good for the normal approximation, but p is small, which is bad. So it’s not obvious whether we can trust the approximation.
An alternative that’s more robust is the Wilson score interval, which is reliable for values of p close to 0 and 1, and sample sizes bigger than about 5.
def confidence_interval_wilson_score(k, n, z): p = k / n factor = z**2 / n denominator = 1 factor center = p factor / 2 half_width = z * np.sqrt((p * (1 - p) factor / 4) / n) lower_bound = (center - half_width) / denominator upper_bound = (center half_width) / denominator return lower_bound, upper_boundHere’s the 90% CI based on Wilson scores.
ci_wilson = confidence_interval_wilson_score(k, n, z)ci_wilson(0.003258660468175958, 0.00405965209814987)Another option is the Clopper-Pearson interval, which is what we computed earlier with the inverse CDF of the binomial distribution. Here’s a function that computes it.
from scipy.stats import binomdef confidence_interval_exact_binomial(k, n, confidence=0.9): alpha = 1 - confidence p = k / n lower_bound = binom.ppf(alpha / 2, n, p) / n if k > 0 else 0 upper_bound = binom.ppf(1 - alpha / 2, n, p) / n if k < n else 1 return lower_bound, upper_boundAnd here’s the interval we get.
ci_binomial = confidence_interval_exact_binomial(k, n)ci_binomial(0.003245800032621106, 0.0040450171260805745)A final alternative is the Jeffreys interval, which is derived from Bayes’s Theorem. If we start with a Jeffreys prior and observe k successes out of n attempts, the posterior distribution of p is a beta distribution with parameters a = k 1/2 and b = n - k 1/2. So we can use the inverse CDF of the beta distribution to compute a CI.
from scipy.stats import betadef bayesian_confidence_interval_beta(k, n, confidence=0.9): alpha = 1 - confidence a, b = k 1/2, n - k 1/2 lower_bound = beta.ppf(alpha / 2, a, b) upper_bound = beta.ppf(1 - alpha / 2, a, b) return lower_bound, upper_boundAnd here’s the interval we get.
ci_beta = bayesian_confidence_interval_beta(k, n)ci_beta(0.003254420914221609, 0.004054683138668112)The following figure shows the four intervals we just computed graphically.
intervals = { 'Normal Approximation': ci_normal, 'Wilson Score': ci_wilson, 'Clopper-Pearson': ci_binomial, 'Jeffreys': ci_beta}y_pos = np.arange(len(intervals))for i, (label, (lower, upper)) in enumerate(intervals.items()): middle = (lower upper) / 2 xerr = [[(middle - lower)], [(upper - middle)]] plt.errorbar(x=middle, y=i-0.2, xerr=xerr, fmt='o', capsize=5) plt.text(middle, i, label, ha='center', va='top') decorate(xlabel='Proportion', ylim=[3.5, -0.8], yticks=[])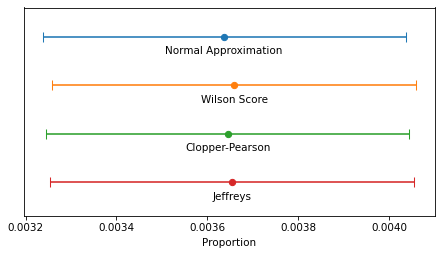
In this example, because n is so large, the intervals are all similar – the differences are too small to matter in practice. For smaller values of n, the normal approximation becomes unreliable, and for very small values, none of them are reliable.
The normal approximation and Wilson score interval are easy and fast to compute. On my old laptop, they take 1-2 microseconds.
%timeit confidence_interval_normal_approx(k, n, z)1.04 µs ± 4.04 ns per loop (mean ± std. dev. of 7 runs, 1,000,000 loops each)%timeit confidence_interval_wilson_score(k, n, z)1.64 µs ± 28.6 ns per loop (mean ± std. dev. of 7 runs, 1,000,000 loops each)Evaluating the inverse CDF of the binomial and beta distributions are more complex computations – they take about 100 times longer.
%timeit confidence_interval_exact_binomial(k, n)195 µs ± 7.53 µs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)%timeit bayesian_confidence_interval_beta(k, n)269 µs ± 4.6 µs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)But they still take less than 300 microseconds, so unless you need to compute millions of confidence intervals per second, the difference in computation time doesn’t matter.
DiscussionIf you took a statistics class and learned one of these methods, you probably learned the normal approximation. That’s because it is easy to explain and, because it is based on a form of the Central Limit Theorem, it helps to justify time spent learning about the CLT. But in my opinion it should never be used in practice because it is dominated by the Wilson score interval – that is, it is worse than Wilson in at least one way and better in none.
I think the Clopper-Pearson interval is equally easy to explain, but when n is small, there are few possible values of k, and therefore few possible values of p – and the interval can be wider than it needs to be.
The Jeffreys interval is based on Bayesian statistics, so it takes a little more explaining, but it behaves well for all values of n and p. And when n is small, it can be extended to take advantage of background information about likely values of p.
For these reasons, the Jeffreys interval is my usual choice, but in a computational environment that doesn’t provide the inverse CDF of the beta distribution, I would use a Wilson score interval.
OP is working in LiveCode, which doesn’t provide a lot of math and statistics libraries, so Wilson might be a good choice. Here’s a LiveCode implementation generated by ChatGPT.
-- Function to calculate the z-score for a 95% confidence level (z ≈ 1.96)function zScore return 1.96end zScore-- Function to calculate the Wilson Score Interval with distinct boundsfunction wilsonScoreInterval k n -- Calculate proportion of successes put k / n into p put zScore() into z -- Common term for the interval calculation put (z^2 / n) into factor put (p factor / 2) / (1 factor) into adjustedCenter -- Asymmetric bounds put sqrt(p * (1 - p) / n factor / 4) into sqrtTerm -- Lower bound calculation put adjustedCenter - (z * sqrtTerm / (1 factor)) into lowerBound -- Upper bound calculation put adjustedCenter (z * sqrtTerm / (1 factor)) into upperBound return lowerBound & comma & upperBoundend wilsonScoreIntervalData Q&A: Answering the real questions with Python
Copyright 2024 Allen B. Downey
September 16, 2024
Ears Are Weird
In a previous article, I looked at 93 measurements from the ANSUR-II dataset and found that ear protrusion is not correlated with any other measurement. In a followup article, I used principle component analysis to explore the correlation structure of the measurements, and found that once you have exhausted the information encoded in the most obvious measurements, the ear-related measurements are left standing alone.
I have a conjecture about why ears are weird: ear growth might depend on idiosyncratic details of the developmental environment — so they might be like fingerprints. Recently I discovered a hint that supports my conjecture.
This Veritasium video explains how we locate the source of a sound.
In general, we use small differences between what we hear in each ear — specifically, differences in amplitude, quality, time delay, and phase. That works well if the source of the sound is to the left or right, but not if it’s directly in front, above, or behind — anywhere on vertical plane through the centerline of your head — because in those cases, the paths from the source to the two ears are symmetric.
Fortunately we have another trick that helps in this case. The shape of the outer ear changes the quality of the sound, depending on the direction of the source. The resulting spectral cues makes it possible to locate sources even when they are on the central plane.
The video mentions that owls have asymmetric ears that make this trick particularly effective. Human ears are not as distinctly asymmetric as owl ears, but they are not identical.
And now, based on the Veritasium video, I suspect that might be a feature — the shape of the outer ear might be unpredictably variable because it’s advantageous for our ears to be asymmetric. Almost everything about the way our bodies grow is programmed to be as symmetric as possible, but ears might be programmed to be different.
September 4, 2024
Rip-off ETF?
An article in a recent issue of The Economist suggests, right in the title, “Investors should avoid a new generation of rip-off ETFs”. An ETF is an exchange-traded fund, which holds a collection of assets and trades on an exchange like a single stock. For example, the SPDR S&P 500 ETF Trust (SPY) tracks the S&P 500 index, but unlike traditional index funds, you can buy or sell shares in minutes.
There’s nothing obviously wrong with that – but as an example of a “rip-off ETF”, the article describes “defined-outcome funds” or buffer ETFs, which “offer investors an enviable-sounding opportunity: hold stocks, with protection against falling prices. All they must do is forgo annual returns above a certain level, often 10% or so.”
That might sound good, but the article explains, “Over the long term, they are a terrible deal for investors. Much of the compounding effect of stock ownership comes from rallies.”
To demonstrate, they use the value of the S&P index since 1980: “An investor with returns capped at 10% and protected from losses would have made a real return of 403% over the period, a fraction of the 3,155% return offered by just buying and holding the S&P 500.”
So that sounds bad, but returns from 1980 to the present have been historically unusual. To get a sense of whether buffer ETFs are more generally a bad deal, let’s get a bigger picture.
Click here to run this notebook on Colab
The Dow JonesThe MeasuringWorth Foundation has compiled the value of the Dow Jones Industrial Average at the end of each day from February 16, 1885 to the present, with adjustments at several points to make the values comparable. The series I collected starts on February 16, 1885 and ends on August 30, 2024. The following cells download and read the data.
DATA_PATH = "https://github.com/AllenDowney/ThinkS... = "DJA.csv"download(DATA_PATH + filename)djia = pd.read_csv(filename, skiprows=4, parse_dates=[0], index_col=0)djia.head()DJIADate1885-02-1630.92261885-02-1731.33651885-02-1831.47441885-02-1931.67651885-02-2031.4252To compute annual returns, we’ll start by selecting the closing price on the last trading day of each year (dropping 2024 because we don’t have a complete year).
annual = djia.groupby(djia.index.year).last().drop(2024)annualDJIADate188539.4859188641.2391188737.7693188839.5866188942.0394……201928538.4400202030606.4800202136338.3000202233147.2500202337689.5400139 rows × 1 columns
Next we’ll compute the annual price return, which is the ratio of successive year-end closing prices.
annual['Ratio'] = annual['DJIA'] / annual['DJIA'].shift(1)annualDJIARatioDate188539.4859NaN188641.23911.044401188737.76930.915861188839.58661.048116188942.03941.061960………201928538.44001.223384202030606.48001.072465202136338.30001.187275202233147.25000.912185202337689.54001.137034139 rows × 2 columns
And the relative return as a percentage.
annual['Return'] = (annual['Ratio'] - 1) * 100Looking at the years with the biggest losses and gains, we can see that most of the extremes were before the 1960s – with the exception of the 2008 financial crisis.
annual.dropna().sort_values(by='Return')DJIARatioReturnDate193177.90000.473326-52.667396190743.03820.622683-37.73174320088776.39000.661629-33.8370971930164.58000.662347-33.765293192071.95000.670988-32.901240…………1954404.39001.43962343.962264190863.11041.46638146.6381031928300.00001.48221348.221344193399.90001.66694566.694477191599.15001.81659981.659949138 rows × 3 columns
Here’s what the distribution of annual returns looks like.
from empiricaldist import Cdfcdf_return = Cdf.from_seq(annual['Return'])cdf_return.plot()decorate(xlabel='Annual return (percent)', ylabel='CDF')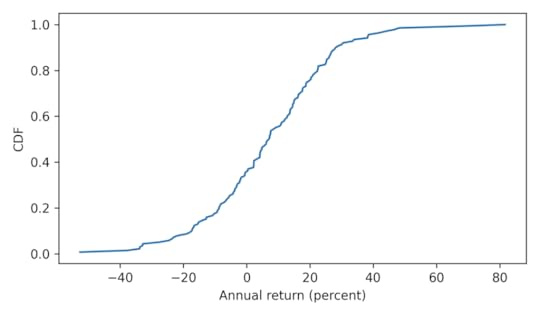
Immediately we see why capping returns at 10% might be a bad idea – this cap is exceeded almost 45% of the time, and sometimes by a lot!
1 - cdf_return(10)0.4492753623188406Long-Term ReturnsWe’ll use the following function to compute long-term returns. It takes a start date and a duration, and computes two ratios:
The total price return based on actual annual returns.The total price return if annual returns are clipped at 0 and 10 – that is, any negative returns are set to 0 and any returns above 10 are set to 10.def compute_ratios(start=1993, duration=30): end = start + duration interval = annual.loc[start: end] ratio = interval['Ratio'].prod() low, high = 1.0, 1.10 clipped = interval['Ratio'].clip(low, high) ratio_clipped = clipped.prod() return start, end, ratio, ratio_clippedWith this function, we can replicate the analysis The Economist did with the S&P 500. Here are the results for the DJIA from the beginning of 1980 to the end of 2023.
compute_ratios(1980, 43)(1980, 2023, 44.93751117788029, 15.356490985533199)A buffer ETF over this period would have grown by a factor of more than 15 in nominal dollars, with no risk of loss. But an index fund would have grown by a factor of almost 45. So yeah, the ETF would have been a bad deal.
However, if we go back to the bad old days, an investor in 1900 would have been substantially better off with a buffer ETF held for 43 years – a factor of 7.2 compared to a factor of 2.8.
compute_ratios(1900, 43)(1900, 1943, 2.8071864303140583, 7.225624631784611)It seems we can cherry-pick the data to make the comparison go either way – so let’s see how things look more generally. Starting in 1886, we’ll compute price returns for all 30-year intervals, ending with the interval from 1993 to 2023.
duration = 30ratios = [compute_ratios(start, duration) for start in range(1886, 2024-duration)]ratios = pd.DataFrame(ratios, columns=['Start', 'End', 'Index Fund', 'Buffer ETF'])ratios.index = ratios['Start']ratios.tail()StartEndIndex FundBuffer ETFStart19891989201913.1600276.53212519901990202011.1166936.36861519911991202113.7976437.00547619921992202210.4604076.36861519931993202311.4172326.724757Here’s what the returns look like for an index fund compared to a buffer ETF.
ratios['Index Fund'].plot()ratios['Buffer ETF'].plot()decorate(xlabel='Start year', ylabel='30-year price return')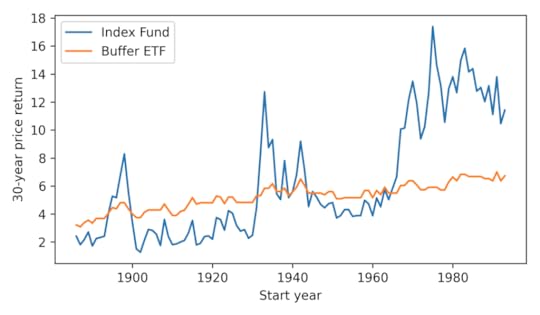
The buffer ETF performs as advertised, substantially reducing volatility. But it has only occasionally been a good deal, and not in my lifetime.
According to ChatGPT, the primary reasons for strong growth in stock prices since the 1960s are “technological advancements, globalization, financial market innovation, and favorable monetary policies”. If you think these elements will generally persist over the next 30 years, you might want to avoid buffer ETFs.
August 23, 2024
Probably the Book
Last week I had the pleasure of presenting a keynote at posit::conf(2024). When the video is available, I will post it here. In the meantime, you can read the slides, if you don’t mind spoilers.
For people at the conference who don’t know me, this might be a good time to introduce you to this blog, where I write about data science and Bayesian statistics, and to Probably Overthinking It, the book based on the blog, which was published by University of Chicago Press last December. Here’s an outline of the book with links to excerpts I’ve published in the blog and talks I’ve presented based on some of the chapters.
For your very own copy, you can order from Bookshop.org if you want to support independent bookstores, or Amazon if you don’t.
Twelve Excellent ChaptersIn Chapter 1, we learn that no one is normal, everyone is weird, and everyone is about the same amount of weird. I published an excerpt from this chapter, and talked about it during this section of the SuperDataScience podcast. And it is featured in an interactive article at Brilliant.org, which includes this animation showing how measurements are distributed in multiple dimensions.

Chapter 2 is about the inspection paradox, which affects our perception of many real-world scenarios, including fun examples like class sizes and relay races, and more serious examples like our understanding of criminal justice and ability to track infectious disease. I published a prototype of this chapter as an article called “The Inspection Paradox is Everywhere“, and gave a talk about it at PyData NYC:
Chapter 3 presents three consequences of the inspection paradox in demography, especially changes in fertility in the United States over the last 50 years. It explains Preston’s paradox, named after the demographer who discovered it: if each woman has the same number of children as her mother, family sizes — and population — grow quickly; in order to maintain constant family sizes, women must have fewer children than their mothers, on average. I published an excerpt from this chapter, and it was discussed on Hacker News.
Chapter 4 is about extremes, outliers, and GOATs (greatest of all time), and two reasons the distribution of many abilities tends toward a lognormal distribution: proportional gain and weakest link effects. I gave a talk about this chapter for PyData Global 2023:
And here’s a related exploration I cut from the book.
Chapter 5 is about the surprising conditions where something used is better than something new. Most things wear out over time, but sometimes longevity implies information, which implies even greater longevity. This property has implications for life expectancy and the possibility of much longer life spans. I gave a talk about this chapter at ODSC East 2024 — there’s no recording, but the slides are here.
Chapter 6 introduces Berkson’s paradox — a form of collision bias — with some simple examples like the correlation of test scores and some more important examples like COVID and depression. Chapter 7 uses collision bias to explain the low birthweight paradox and other confusing results from epidemiology. I gave a “Talk at Google” about these chapters:
Chapter 8 shows that the magnitudes of natural and human-caused disasters follow long-tailed distributions that violate our intuition, defy prediction, and leave us unprepared. Examples include earthquakes, solar flares, asteroid impacts, and stock market crashes. I gave a talk about this chapter at SciPy 2023:
The talk includes this animation showing how plotting a tail distribution on a log-y scale provides a clearer picture of the extreme tail behavior.

Chapter 9 is about the base rate fallacy, which is the cause of many statistical errors, including misinterpretations of medical tests, field sobriety tests, and COVID statistics. It includes a discussion of the COMPAS system for predicting criminal behavior.
Chapter 10 is about Simpson’s paradox, with examples from ecology, sociology, and economics. It is the key to understanding one of the most notorious examples of misinterpretation of COVID data. This is the first of three chapters that use data from the General Social Survey (GSS).
Chapter 11 is about the expansion of the Moral Circle — specifically about changes in attitudes about race, gender, and homosexuality in the U.S. over the last 50 years. I published an excerpt about the remarkable decline of homophobia since 1990, featuring lyrics from “A Message From the Gay Community“.
Chapter 12 is about the Overton Paradox, a name I’ve given to a pattern observed in GSS data: as people get older, their beliefs become more liberal, on average, but they are more likely to say they are conservative. This chapter is the basis of this interactive lesson at Brilliant.org. And I gave a talk about it at PyData NYC 2022:
There are still a few chapters I haven’t given a talk about, so watch this space!
Again, you can order the book from Bookshop.org if you want to support independent bookstores, or Amazon if you don’t.
Supporting code for the book is in this GitHub repository. All of the chapters are available as Jupyter notebooks that run in Colab, so you can replicate my analysis. If you are teaching a data science or statistic class, they make good teaching examples.
Chapter 1: Are You Normal? Hint: No.
Run the code that prepares the BRFSS data
Run the code that prepares the Big Five data
Chapter 2: Relay Races and Revolving Doors
Chapter 3: Defy Tradition, Save the World
Chapter 4: Extremes, Outliers, and GOATs
Run the code that prepares the BRFSS data
Run the code that prepares the NSFG data
Chapter 5: Bettter Than New
Chapter 6: Jumping to Conclusions
Chapter 7: Causation, Collision, and Confusion
Run the code that prepares the NCHS data
Chapter 8: The Long Tail of Disaster
Run the code that prepares the earthquake data
Run the code that prepares the solar flare data
Chapter 9: Fairness and Fallacy
Chapter 10: Penguins, Pessimists, and Paradoxes
Run the code that prepares the GSS data
Chapter 11: Changing Hearts and Minds
Chapter 12: Chasing the Overton Window
Probably Overthinking It
- Allen B. Downey's profile
- 236 followers



