John C. Baez's Blog, page 26

The Kepler Problem (Part 3)

The Kepler problem studies a particle moving in an inverse square force, like a planet orbiting the Sun. Last time I talked about an extra conserved quantity associated to this problem, which keeps elliptical orbits from precessing or changing shape. This extra conserved quantity is sometimes called the Laplace–Runge–Lenz vector, but since it was first discovered by none of these people, I prefer to call it the ‘eccentricity vector’

In 1847, Hamilton noticed a fascinating consequence of this ...

The Periodic Table

 

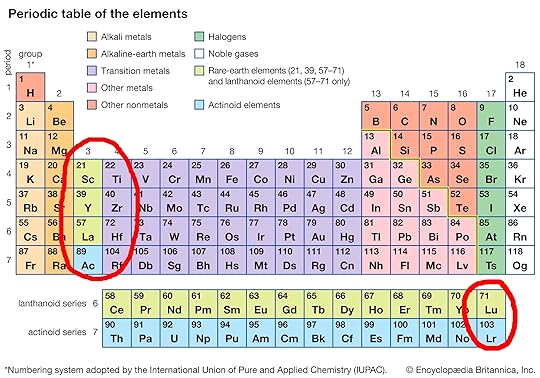
I like many kinds of periodic table, but hate this one. See the problem?

Element 57 is drawn right next to element 72, replacing the element that should be there: element 71. So lutetium, element 71, is being denied its rightful place as a transition metal and is classified as a rare earth. Meanwhile lanthanum, element 57, which really is a rare earth, is drawn separately from all the rest! This is especially ironic because those rare earths are called ‘lanthanoids’ or ‘lanthanides’.

Si...

Rapid Variable B Subdwarf Stars

 

A subdwarf B star is a blue-hot star smaller than the Sun. A few of these crazy stars pulse in brightness as fast as every 90 seconds! Waves of ionizing iron pulse through their thin surface atmosphere.

What’s up with these weird stars?

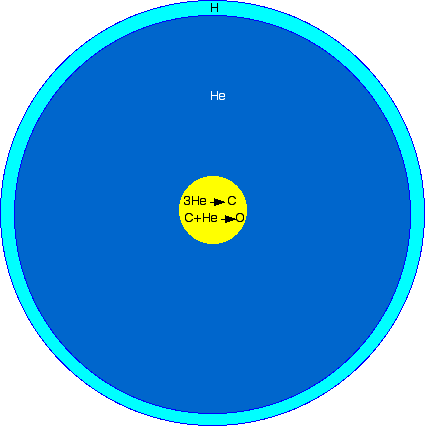
Sometimes a red giant loses most of its outer hydrogen… nobody is sure why… leaving just a thin layer of hydrogen over its helium core. We get a star with at most 1/4 the diameter of the Sun, but really hot.

It’s the blue-hot heart of a red giant, ...

The Color of Infinite Temperature

 

This is the color of something infinitely hot. Of course you’d instantly be fried by gamma rays of arbitrarily high frequency, but this would be its spectrum in the visible range.

This is also the color of a typical neutron star. They’re so hot they look the same.

It’s also the color of the early Universe!

This was worked out by David Madore.

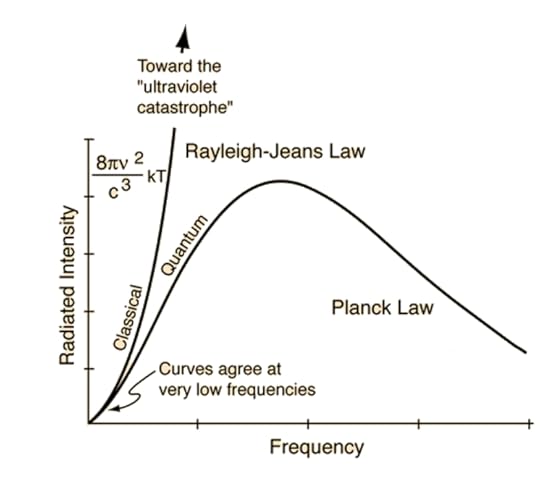
As a blackbody gets hotter and hotter, its spectrum approaches the classical Rayleigh–Jeans law. That is, its true spectrum as given by the Pl...

Adjoint School 2022

Every year since 2018 we’ve been having annual courses on applied category theory where you can do research with experts. It’s called the Adjoint School.

You can apply to be a student at the 2022 Adjoint School now, and applications are due January 29th! Go here:

• 2022 Adjoint School: application.

The school will be run online from February to June, 2022, and then—coronavirus permitting—there will be in-person research at the University of Strathclyde in Glasgow, Scotland the week of July 11...

The Kepler Problem (Part 2)

I’m working on a math project involving the periodic table of elements and the Kepler problem—that is, the problem of a particle moving in an inverse square force law. That’s one reason I’ve been blogging about chemistry lately! I hope to tell you all about this project sometime—but right now I just want to say some very basic stuff about the ‘eccentricity vector’.

This vector is a conserved quantity for the Kepler problem. It was named the ‘Runge–Lenz vector’ after Lenz used it in 1924 to...

Clemens non Papa

As I’ve explored more music from the Franco-Flemish school, I’ve gotten to like some of the slightly less well-known composers—though usually famous in their day—such as Jacobus Clemens non Papa, who lived in Flanders from roughly 1510 to 1555. I enjoy his clear, well-balanced counterpoint. It’s peppy, well-structured, but unromantic: no grand gestures or strong emotions, just lucid clarity. That’s quite appealing to me these days.

On a website about Flemish music I read that:

The style of ...

The Binary Octahedral Group (Part 2)

Part 1 introduced the ‘binary octahedral group’. This time I just want to show you some more pictures related to this group. I’ll give just enough explanation to hint at what’s going on. For more details, check out this webpage:

• Greg Egan, Symmetries and the 24-cell.

Okay, here goes!

You can inscribe two regular tetrahedra in a cube:

Each tetrahedron has 4! = 24 symmetries permuting its 4 vertices.

The cube thus has 48 symmetries, twice as many. Half map each tetrahedron to itself, ...

Photon-Photon Scattering

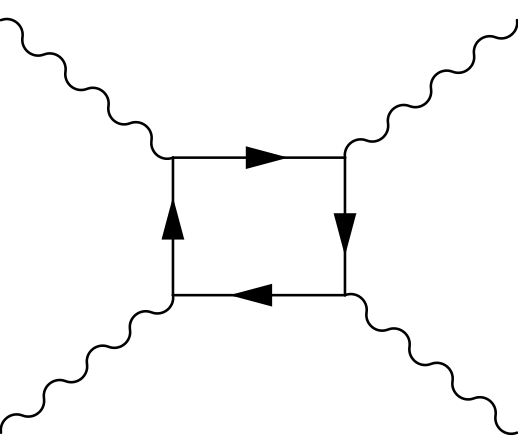
Light can bounce off light by exchanging virtual charged particles! This gives nonlinear corrections to Maxwell’s equations, even in the vacuum—but they’re only noticeable when the electric field is about 1018 volts/meter or more. This is an enormous electric field, able to accelerate a proton from rest to Large Hadron Collider energies in just 5 micrometers!

In 2017, light-on-light scattering was seen at the LHC when they shot lead ions past each other:

Direct evidence for light-by-light ...

Transition Metals

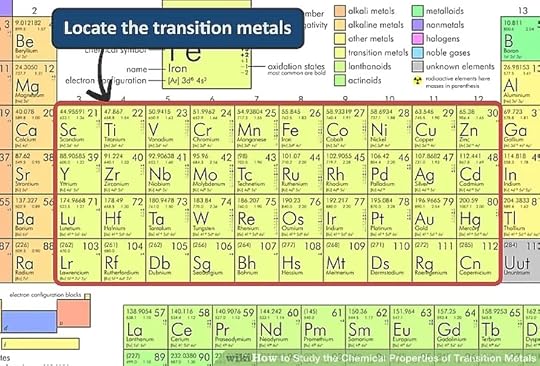
The transition metals are more complicated than lighter elements.

Why?

Because they’re the first whose electron wavefunctions are described by quadratic functions of 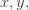and — not just linear or constant. These are called ‘d orbitals’, and they look sort of like this:

More precisely: the wavefunctions of electrons in atoms depend on the distance from the nucleus and also the angles 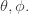The angular dependence is described by ‘spherical harmonics’, certain functions on the sphere. These ar...