John C. Baez's Blog, page 28

The Kuramoto–Sivashinsky Equation (Part 3)

I’ve been getting a lot of help from Steve Huntsman and also Cheyne Weis, who is a physics grad student at the University of Chicago. You can see a lot, but far from all, of Steve’s work as comments on part 1. Here are some things Cheyne has been doing.

Cheyne started out working with the ‘derivative form’ of the Kuramoto–Sivashinsky equation, meaning this:

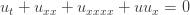
and he soon noticed what Steve made clear in the image above: the ‘stripes’ in solutions of this equation aren’t ‘bumps’ (regions wher...

The Kuramoto–Sivashinsky Equation (Part 2)

I love the Kuramoto–Sivashinsky equation, beautifully depicted here by Thien An, because it’s one of the simplest partial differential equations that displays both chaos and a visible ‘arrow of time’. Last time I made some conjectures about it. Most notably, I conjecture that the ‘stripes’ you see above can appear or merge as time passes, but never disappear or split.

But I was quite confused for a while, because the Kuramoto–Sivashinsky equation comes in two forms. The integral form, which...

Topos Institute Postdoc

The Topos Institute is trying to hire a postdoc to work on polynomial functors! Here is the ad, written by David Spivak.

Dear all,

I’m happy to announce that Topos Institute is hiring a postdoctoral research fellow to study polynomial functors and their applications. A mathjobs listing is here:

https://www.mathjobs.org/jobs/list/18637

and information on the precise project can be found here:

http://www.dspivak.net/grants/AFOSR2020-Topos-Supplement2021.pdf

Applicants should be strong in math...

The Kuramoto–Sivashinsky Equation (Part 1)

I love this movie showing a solution of the Kuramoto–Sivashinsky equation, made by Thien An. If you haven’t seen her great math images on Twitter, check them out!

I hadn’t known about this equation, and it looked completely crazy to me at first. But it turns out to be important, because it’s one of the simplest \partial differential equations that exhibits chaotic behavior.

As the image scrolls to the left, you’re seeing how a real-valued function 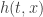of two real variables changes with the pass...

Conjectures on the Kuramoto–Sivashinsky Equation

I love this movie showing a solution of the Kuramoto–Sivashinsky equation, made by Thien An. If you haven’t seen her great math images on Twitter, check them out!

I hadn’t known about this equation, and it looked completely crazy to me at first. But it turns out to be important, because it’s one of the simplest partial differential equations that exhibits chaotic behavior.

As the image scrolls to the left, you’re seeing how a real-valued
function 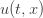of two real variables changes with the passa...

Stirling’s Formula in Words

 

I recently sketched a quick proof of Stirling’s asymptotic formula for the factorial. But what does this formula really mean?

Above is my favorite explanation. You can’t see the number in the words here, but it’s hiding in the formula for a Gaussian probability distribution. But what about the factorial, and the rest?

My description in words was informal. I’m really talking about a
Poisson distribution. If raindrops land at an average rate 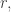this says that after time the probability of...

Nonequilibrium Thermodynamics in Biology

William Cannon and I are organizing a special session on thermodynamics in biology at the American Physical Society March Meeting, which will be held in Chicago on March 14–18, 2022.

If you work on this, please submit an abstract here before October 22! Our session number is 03.01.32.

Non-equilibrium Thermodynamics in Biology: from Chemical Reaction Networks to Natural Selection

Since Lotka, physical scientists have argued that living things belong to a class of complex and orderly systems that...

Stirling’s Formula

Stirling’s formula says

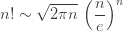
where means that the ratio of the two quantities goes to as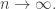

Where does this formula come from? In particular, how does the number get involved? Where is the circle here?

To understand these things, I think a nonrigorous argument that can be made rigorous is more useful than a rigorous proof with all the ε’s dotted and the δ’s crossed. It’s important, I think, to keep the argument short. So let me do that.

The punchline will be that the comes from this formula:

...

Classical Mechanics versus Thermodynamics (Part 4)

Thanks to the precise mathematical analogy between classical mechanics and thermodynamics that we saw last time, we can define Poisson brackets in thermodynamics just as in classical mechanics. That is, we can define Poisson brackets of quantities like entropy, temperature, volume and pressure. But what does this mean?

Furthermore, we can get quantum mechanics from classical mechanics by replacing Poisson brackets by commutators. That’s a brief summary of a long story, but by now this story ...

Classical Mechanics versus Thermodynamics (Part 3)

There’s a fascinating analogy between classical mechanics and thermodynamics, which I last talked about in 2012:

• Classical mechanics versus thermodynamics (part 1).
• Classical mechanics versus thermodynamics (part 2).

I’ve figured out more about it, and today I’m giving a talk about it in the physics colloquium at the University of British Columbia. It’s a colloquium talk that’s supposed to be accessible for upper-level undergraduates, so I’ll spend a lot of time reviewing the basics… which ...