John C. Baez's Blog, page 29

Maxwell’s Relations (Part 3)

In Part 2 we saw a very efficient formulation of Maxwell’s relations, from which we can easily derive their usual form. Now let’s talk more about the meaning of the Maxwell relations—both their physical meaning and their mathematical meaning. For the physical meaning, I’ll draw again from Ritchie’s paper:

• David J. Ritchie, A simple method for deriving Maxwell’s relations, American Journal of Physics 36 (1958), 760–760.

but Emily Roach pointed out that much of this can also be found in the th...

Maxwell’s Relations (Part 2)

The Maxwell relations are some very general identities about the partial derivatives of functions of several variables. You don’t need to understand anything about thermodyamics to understand them, but they’re used a lot in that subject, so discussions of them tend to use notation from that subject.

Last time I went through a standard way to derive these relations for a function of two variables. Now I want to give a better derivation, which I found here:

• David J. Ritchie, A simple method fo...

Maxwell’s Relations (Part 1)

The Maxwell relations are equations that show up whenever we have a finite-dimensional vector space 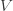and a smooth convex function

They say that the mixed partial derivatives of commute, but also that the mixed partial derivatives of various functions constructed from 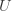commute. So in a sense they are completely trivial except for the way we construct these various functions! Nonetheless they are very important in physics, because they give generally valid relations between the derivatives of...

The Cyclic Identity for Partial Derivatives

 

As an undergrad I learned a lot about partial derivatives in physics classes. But they told us rules as needed, without proving them. This rule completely freaked me out. If derivatives are kinda like fractions, shouldn’t this equal 1?

Let me show you why it’s -1.

First, consider an example:

This example shows that the identity is not crazy. But in fact it
holds the key to the general proof! Since 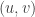is a coordinate system we can assume without loss of generality that . At any point w...

Information Geometry (Part 21)

Last time I ended with a formula for the ‘Gibbs distribution’: the probability distribution that maximizes entropy subject to constraints on the expected values of some observables.

This formula is well-known, but I’d like to derive it here. My argument won’t be up to the highest standards of rigor: I’ll do a bunch of computations, and it would take more work to state conditions under which these computations are justified. But even a nonrigorous approach is worthwhile, since the computation...

Information Geometry (Part 20)

Last time we worked out an analogy between classical mechanics, thermodynamics and probability theory. The latter two look suspiciously similar:

 Classical Mechanics  Thermodynamics  Probability Theory  q  positionextensive variablesprobabilities p  momentumintensive variablessurprisals S   actionentropy Shannon entropy

This is no coincidence. After all, in the subject of statistical mechanics we explain classical thermodynamics using probability theory—and entropy...

Information Geometry (Part 19)

Last time I figured out the analogue of momentum in probability theory, but I didn’t say what it’s called. Now I will tell you—thanks to some help from Abel Jansma and Toby Bartels.

SURPRISE: it’s called SURPRISAL!

This is a well-known concept in information theory. It’s also called ‘information content‘.

Let’s see why. First, let’s remember the setup. We have a manifold

whose points 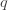are nowhere vanishing probability distributions on the set We have a function

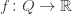
called the Shannon entro...

Information Geometry (Part 18)

Last time I sketched how two related forms of geometry, symplectic and contact geometry, show up in thermodynamics. Today I want to explain how they show up in probability theory.

For some reason I haven’t seen much discussion of this! But people should have looked into this. After all, statistical mechanics explains thermodynamics in terms of probability theory, so if some mathematical structure shows up in thermodynamics it should appear in statistical mechanics… and thus ultimately in prob...

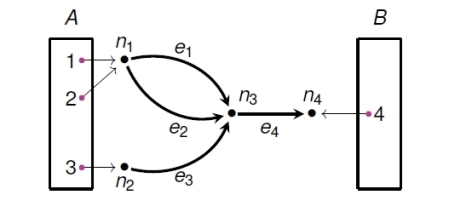
Structured vs Decorated Cospans (Part 2)

Decorated cospans are a framework for studying open systems invented by Brendan Fong. Since I’m now visiting the institute he and David Spivak set up—the Topos Institute—it was a great time to give a talk explaining the history of decorated cospans, their problems, and how those problems have been solved:

Structured vs Decorated Cospans

Abstract. One goal of applied category theory is to understand open systems: that is, systems that can interact with the external world. We compare two appr...

Information Geometry (Part 17)

I’m getting back into information geometry, which is the geometry of the space of probability distributions, studied using tools from information theory. I’ve written a bunch about it already, which you can see here:

• Information geometry.

Now I’m fascinated by something new: how symplectic geometry and contact geometry show up in information geometry. But before I say anything about this, let me say a bit about how they show up in thermodynamics. This is more widely discussed, and it’s a g...