John C. Baez's Blog, page 2

The Cosmic Horseshoe

Astronomers have found a truly huge black hole! It’s in the massive galaxy in the center here, called the Cosmic Horseshoe. The blue ring is light from a galaxy behind the Cosmic Horseshoe, severely bent by gravity.

This black hole is 36 billion times the mass of the Sun. It’s not just ‘supermassive’: any black hole over 10 billion times the Sun’s mass is considered ‘ultramassive’. Not many have been found. T

To me the coolest part is that the Cosmic Horseshoe has swallowed all the ot...

Safeguarded AI Meeting

This week, 50 category theorists and software engineers working on “safeguarded AI” are meeting in Bristol. They’re being funded by £59 million from ARIA, the UK’s Advanced Research and Invention Agency.

The basic idea is to develop a mathematical box that can contain a powerful genie. More precisely:

“By combining scientific world models and mathematical proofs we will aim to construct a ‘gatekeeper’, an AI system tasked with understanding and reducing the risks of other AI agents. ...

The Kepler Problem (Part 11)

In Part 9 we saw, loosely speaking, that the theory of a hydrogen atom is equivalent to the theory of a massless left-handed spin-½ particle in the Einstein universe—a static universe where space is a 3-sphere. Today we’ll ‘second quantize’ both of these equivalent theories and get new theories that again are equivalent.

‘Second quantization’ is a funny term. It’s a completely systematic way to get a new quantum theory from an old one. When you second quantize the theory of some particle, ...

The Kepler Problem (Part 10)

The poet Blake wrote that you can

see a world in a grain of sand.

Today we’ll see a universe in an atom!

We’ll see that states of the hydrogen atom correspond to states of a massless spin-½ particle in the Einstein universe—a closed, static universe where space is a 3-sphere.

The rotational symmetries of the Einstein universe correspond to symmetries of the hydrogen atom. The energy eigenstates of the massless spin-½ particle correspond in a one-to-one way to energy eigenstates of the hydrog...

The Kepler Problem (Part 9)

Today I want to make a little digression into the quaternions. We won’t need this for anything later—it’s just for fun. But it’s quite beautiful.

We saw in Part 8 that if we take the spin of the electron into account, we can think of bound states of the hydrogen atom as spinor-valued functions on the 3-sphere. Here a ‘spinor’ is a pair of complex numbers.

But we can also think of a spinor as a quaternion! And we can think of the 3-sphere as the unit sphere in the quaternions! So bound sta...

The Kepler Problem (Part 8)

Now comes the really new stuff. I want to explain how the hydrogen atom is in a certain sense equivalent to a massless spin-½ particle in the ‘Einstein universe’. This is the universe Einstein believed in before Hubble said the universe was expanding! It has a 3-sphere 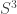for space, and this sphere stays the same size as time passes.

Today I’ll just lay the groundwork. To study relativistic spin-½ quantum particles, we need to understand the Dirac operator. So, we need to bring out the ge...

Lawvere’s Work on Arms Control

Did you know that Lawvere did classified work on arms control in the 1960s, back when he was writing his thesis? Did you know that the French government offered him a job in military intelligence?

The following paper should be interesting to applied category theorists—for a couple of different reasons:

• Bill Lawvere, The category of probabilistic mappings with applications to stochastic processes, statistics, and pattern recognition, Spring 1962, featuring Lawvere’s abstract and author commen...

The Kepler Problem (Part 7)

I’ve explained a cool way to treat bound states of the hydrogen atom as wavefunctions on a sphere in 4-dimensional space. But so far I’ve been neglecting the electron’s spin. Now let’s throw that in too!

This will wind up leading us in some surprising directions. So far I’ve just been reviewing known ideas, but now we’re getting into my new paper:

• Second quantization for the Kepler problem.

It starts out being quite routine: to include spin, we just tensor our previous Hilbert space 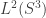with a...

The Kepler Problem (Part 6)

In Part 4 we saw that the classical Kepler problem—the problem of a single classical particle in an inverse square force—has symmetry under the group of rotations of 4-dimensional space 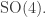Since the Lie algebra of this group is

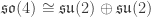
we must have conserved quantities

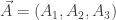
and

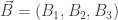
corresponding to these two copies of 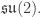The physical meaning of these quantities is a bit obscure until we form linear combinations

Then 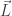is the angular momentum of the particle, while 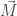is a subtler conserved quantity: it’s the ecc...

The Kepler Problem (Part 5)

In Part 4 we saw how the classical Kepler problem is connected to a particle moving on the 3-sphere, and how this illuminates the secret 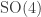symmetry of the Kepler problem. There are various ways to quantize the Kepler problem and obtain a description of the hydrogen atom’s bound states as wavefunctions on the 3-sphere. Here I’ll take a less systematic but quicker approach.

I’ll start with the space of wavefunctions on the 3-sphere, 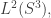and describe operators on this space arising from rotational sy...