John C. Baez's Blog, page 27

The Madelung Rules

I’ve been thinking about chemistry lately. I’m always amazed by how far we can get in the study of multi-electron atoms using ideas from the hydrogen atom, which has just one electron.

If we ignore the electron’s spin and special relativity, and use just Schrödinger’s equation, the hydrogen atom is exactly solvable—and a key part of any thorough introduction to quantum mechanics. So I’ll zip through that material now, saying just enough to introduce the ‘Madelung rules’, which are two incredib...

Surveillance Publishing

Björn Brembs recently explained how

“massive over-payment of academic publishers has enabled
them to buy surveillance technology covering the entire workflow that can be used not only to be combined with our private data and sold, but also to make algorithmic (aka ‘evidenceled’) employment decisions.”

Reading about this led me to this article:

• Jefferson D. Pooley, Surveillance publishing.

It’s all about what publishers are doing to make money by collecting data on the habits of their rea...

Benzene

The structure of benzene is fascinating. Look at all these different attempts to depict it! Let me tell you a tiny bit of the history.

In 1865, August Kekulé argued that benzene is a ring of carbon atoms with alternating single and double bonds. Later, at a conference celebrating the 25th anniversary of this discovery, he said he realized this after having a daydream of a snake grabbing its own tail.

Kekulé’s model was nice, because before this it was hard to see how 6 carbons and 6 hydro...

Anthocyanins

 

As the chlorophyll wanes, now is the heyday of the xanthophylls,
carotenoids and anthocyanins. These contain carbon rings and chains whose electrons become delocalized… their wavefunctions resonating at different frequencies, emitting photons of yellow, orange and red!

Yes, it’s fall. I’m enjoying it.

I wrote about two xanthophylls in my May 27, 2014 diary entry: I explained how they get their color from the resonance of delocalized electrons that spread all over a carbon ...

Compositional Thermostatics

At the Topos Institute this summer, a group of folks started talking about thermodynamics and category theory. It probably started because Spencer Breiner and my former student Joe Moeller, both working at NIST, were talking about thermodynamics with some people there. But I’ve been interested in thermodynamics for quite a while now, and Owen Lynch, a grad student visiting from the University of Utrecht, wants to do his master thesis on this subject. And Sophie Libkind, David Spivak and Dav...

The Kuramoto–Sivashinsky Equation (Part 7)

I have a lot of catching up to do. I want to share a bunch of work by Steve Huntsman. I’ll start with some older material. A bit of this may be ‘outdated’ by his later work, but I figure it’s all worth recording.

One goal here is to define ‘stripes’ for the Kuramoto–Sivashinky equation in a way that lets us count them, their births, and their mergers, and so on. We need a good definition to test the conjectures I made in Part 1.

While I originally formulated my conjectures for the ‘integral...

Learn Applied Category Theory!

Do you like the idea of learning applied category theory by working on a project, as part of a team led by an expert? If you’re an early career researcher you can apply to do that now!

• Mathematical Research Community: Applied Category Theory, meeting 2022 May 29–June 4. Details on how to apply: here. Deadline to apply: Tuesday 2022 February 15 at 11:59 Eastern Time.

After working with your team online, you’ll take an all-expenses-paid trip to a conference center in upstate New York for a we...

The Kuramoto–Sivashinsky Equation (Part 6)

guest post by Theodore Kolokolnikov

I coded up a simple dynamical system with the following rules (loosely motivated by theory of motion of spikes in reaction-diffusion systems, see e.g. appendix of this paper, as well as this paper):

• insert a particle if inter-particle distance is more than some maxdist
• merge any two particles that collide
• otherwise evolve particles according to the ODE

Here, 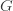is a Green’s function that satisfies

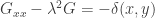
inside the interval with Neumann boundary conditions 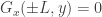. E...

The Kuramoto–Sivashinsky Equation (Part 5)

In Parts 3 and 4, I showed some work of Cheyne Weis on the ‘derivative form’ of the Kuramoto–Sivashinksy equation, namely

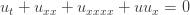
Steve Huntsman’s picture of a solution above gives you a good feel for how this works.

Now let’s turn to the ‘integral form’, namely

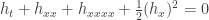
This has rather different behavior, though it’s closely related, since if 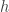is any solution of the integral form then

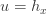
is a solution of the derivative form.

Cheyne drew a solution of the integral form:

You’ll immediately see the most promi...

The Kuramoto–Sivashinsky Equation (Part 4)

Here is some more work by Cheyne Weis. Last time I explained that Cheyne and Steve Huntsman were solving the ‘derivative form’ of the Kuramoto–Sivashinsky equation, namely this:

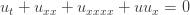
Above is one of Steve’s pictures of a typical solution with its characteristic ‘stripes’. Cheyne started trying to identify these stripes as locations where 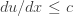for some cutoff 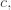for example 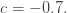He made some nice 3d views of 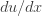illustrating the problems with this. As he explains:

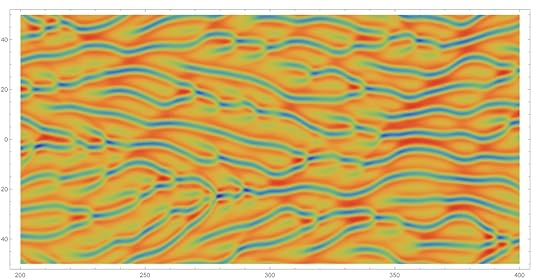
So there is the tradeoff that if I ...