John C. Baez's Blog, page 23

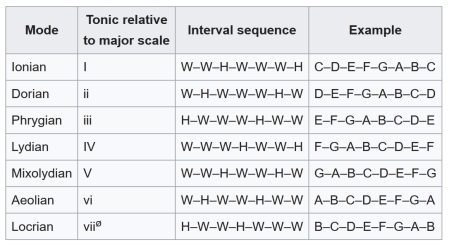
Modes

I’ve been away from my piano since September. I really miss playing it. So, I’ve been sublimating my desire to improvise on this instrument by finally learning a bunch of basic harmony theory, which I practice just by singing or whistling.

For example, I’m getting into modes. The following 7 modes are all obtained by taking the major scale and starting it at different points. But I find that’s not the good way for me to understand the individual flavor of each one.

Much better for me is to ...

This Week’s Finds – Lecture 6

 

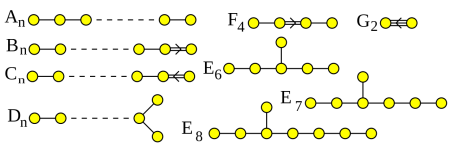
Coxeter and Dynkin diagrams classify some of the most beautiful objects in mathematics. Here I use Dynkin diagrams to classify compact Lie groups—and especially compact semisimple Lie groups.

This is one of a series of lectures at the University of Edinburgh on topics drawn from my column This Week’s Finds:

http://math.ucr.edu/home/baez/twf/

Cover image by Tom Ruen, CC BY-SA 4.0

This Week’s Finds – Lecture 5

 

Coxeter and Dynkin diagrams classify some of the most beautiful objects in mathematics. Here I explain how Dynkin diagrams classify root lattices.

For more, read my paper “Coxeter and Dynkin diagrams” here:

http://math.ucr.edu/home/baez/twf/

To attend the talks on Zoom go here.

This Week’s Finds – Lecture 4

 

Coxeter and Dynkin diagrams classify some of the most beautiful objects in mathematics. Here I explain how Coxeter groups classify finite reflection groups: that is, finite groups of transformations of 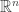generated by reflections.

For more, read my paper “Coxeter and Dynkin diagrams” here:

http://math.ucr.edu/home/baez/twf/

To attend the talks on Zoom go here.

Coxeter and Dynkin Diagrams

Coxeter and Dynkin diagrams classify a wide variety of structures, most notably finite reflection groups, lattices having such groups as symmetries, compact simple Lie groups and complex simple Lie algebras. The simply laced or ‘ADE’ Dynkin diagrams also classify finite subgroups of SU(2) and quivers with finitely many indecomposable representations.

I’m talking about Coxeter and Dynkin diagrams now in my This Week’s Finds seminars. I started in Lecture 4, which you can see on video already, a...

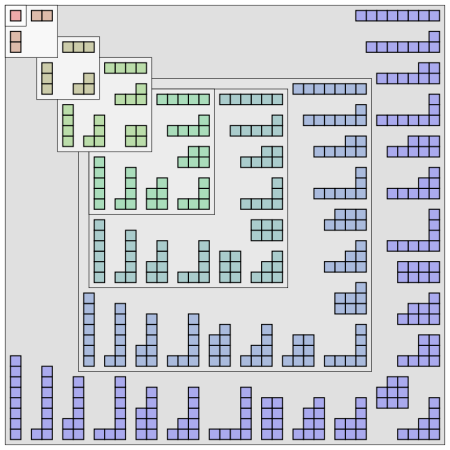
This Week’s Finds – Lecture 3

Young diagrams are combinatorial structures that show up in a myriad of applications. Here we explain how to classify irreducible representations of classical groups, and especially the “full linear monoid” consisting of all n × n complex matrices, using Young diagrams.

For the full story on representations of the classical groups, read my paper “Young diagrams and classical groups” here:

http://math.ucr.edu/home/baez/twf/

To attend the talks on Zoom go here.

The Kuramoto–Sivashinsky Equation (Part 8)

Our paper on the Kuramoto–Sivashinsky equation is out!

• John Baez, Steve Huntsman and Cheyne Weis, The Kuramoto–Sivashinsky equation, Notices Amer. Math. Soc. 69 (2022), 1581–1583.

This equation displays chaos and an arrow of time—and we state a precise conjecture about it, which may be very hard to prove, but is easy to study numerically. Steve Huntsman has written MATLAB code to help you do this, and I can make that available if you’re interested.

So what’s the idea? The article is short so...

This Week’s Finds – Lecture 2

 

Young diagrams are combinatorial structures that show up in a myriad of applications. Here we explain how to classify irreducible representations of the symmetric groups Sₙ using Young diagrams. Then we introduce some ‘classical groups’ – famous groups whose irreducible representations can also be classified using Young diagrams.

For more details, read my paper “Young diagrams and classical groups” here:

http://math.ucr.edu/home/baez/twf/

To attend the talks on Zoom go here.

By the way: th...

This Week’s Finds – Lecture 1

 

Young diagrams are combinatorial structures that show up in a myriad of applications. In this talk I explain how Young diagrams classify conjugacy classes in the symmetric groups, introduce the representation theory of finite groups, and start to explain how Young diagrams classify irreducible representations of the symmetric groups.

For more details, read my paper “Young diagrams and classical groups” here:

http://math.ucr.edu/home/baez/twf/

To attend the talks on Zoom go here.

Young Diagrams and Classical Groups

Young diagrams can be used to classify an enormous number of things.   My first one or two This Week’s Finds seminars will be on Young diagrams and classical groups. Here are some lecture notes:

• Young diagrams and classical groups.

I probably won’t cover all this material in the seminar. The most important part is the stuff up to and including the classification of irreducible representations of the “classical monoid” End(Cn). (People don’t talk about classical monoids, but they should.)

Jus...