John C. Baez's Blog, page 22

This Week’s Finds – Lecture 9

 

In this talk I explained the quaternions and octonions, and showed how to multiply them using the dot product and cross product of vectors.

For more details, including a proof that octonion multiplication obeys |ab|=|a||b|, go here:

• Octonions and the Standard Model (Part 2).

This was one of a series of lectures based on my column This Week’s Finds.

 

 

This Week’s Finds – Lecture 8

 

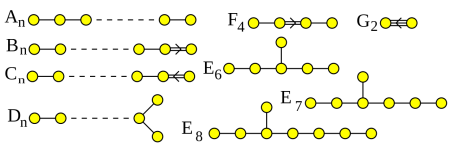
In this talk I explained the E8 root lattice and how it gives rise to the ‘octooctonionic projective plane’, a 128-dimensional manifold on which the compact Lie group called E8 acts as symmetries. I also discussed how some special root lattices give various notions of ‘integer’ for the real numbers, complex numbers, quaternions and octonions.

For more, read my paper Coxeter and Dynkin diagrams.

This was one of a series of lectures based on my column This Week’s Finds.

Mathematics for Humanity

I’m working with an organization that may eventually fund proposals to fund workshops for research groups working on “mathematics for humanity”. This would include math related to climate change, health, democracy, economics, etc.

I can’t give details unless and until it solidifies.

However, it would help me to know a bunch of possible good proposals. Can you help me imagine some?

A good proposal needs:

• a clearly well-defined subject where mathematics is already helping humanity but could help...

The Icosidodecahedron

The icosidodecahedron can be built by truncating either a regular icosahedron or a regular dodecahedron. It has 30 vertices, one at the center of each edge of the icosahedron—or equivalently, one at the center of each edge of a dodecahedron. It is a beautiful, highly symmetrical shape. But it is just a shadow of a more symmetrical shape with twice as many vertices, which lives in a space with twice as many dimensions! Namely, it is a projection down to 3d space of a 6-dimensional polytope wi...

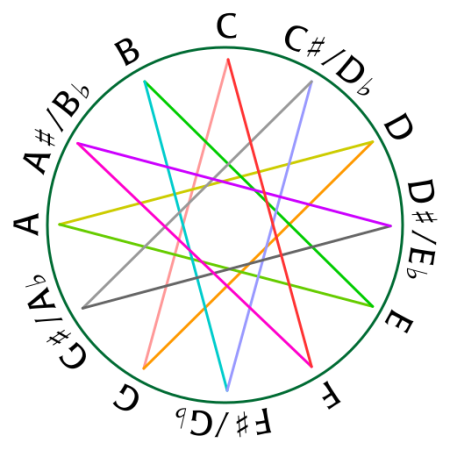
The Circle of Fifths

The circle of fifths is a beautiful thing, fundamental to music theory.

Sound is vibrations in air. Start with some note on the piano. Then play another note that vibrates 3/2 times as fast. Do this 12 times. Since

(3/2)¹² ≈ 128 = 2⁷

when you’re done your note vibrates about 2⁷ times as fast as when you started!

Notes have letter names, and two notes whose frequencies differ by a power of 2 have the same letter name. So the notes you played form a 12-pointed star:

Each time you inc...

This Week’s Finds – Lecture 7

Today I’ll be talking about quaternions, octonions and E8. But a warning to everyone: today, November 10th, the seminar will be in a different building.

Today we’re in Lecture Theatre 1 of the Daniel Rutherford Building. This is a few minutes’ walk from the James Clerk Maxwell Building, just along from the Darwin Building.

Next week we will return to the usual place: Room 6206 of the James Clerk Maxwell Building, home of the Department of Mathematics of the University of Edinburgh.

As usual yo...

Modes (Part 2)

When you first learn about the major scale it’s fairly straightforward, because they tell you about just one major scale. But the minor scale is more tricky, because they tell you about three—or actually four, two of which are the same!

The most fundamental of these is the natural minor scale. The C major scale goes

C D E F G A B C

The C natural minor scale goes

C D E♭ F G A♭ B♭ C

As you can see the 3rd, 6th and 7th notes of the scale are ‘flatted’: moved down a half-tone compared to the major...

Sundial Puzzle

I’ve quit explaining math on Twitter and moved my activities of that sort to Mathstodon. This is a branch of Mastodon, a federated social network that is run by its own users—not by an unpredictable self-centered billionaire.

It feels a lot like the internet of the late 80’s or early 90’s, with people pitching in to build things they themselves use, not serving as cogs in the giant machine of surveillance capitalism. I invite you to join us!

I plan to write things there, polish them up a bit a...

Categories and Epidemiology

 

Tomorrow I’m talking about my work using category theory to help design software for epidemic modeling:

• Category theory and epidemiology, African Mathematics Seminar, Wednesday November 2, 2022, 3 pm Nairobi time or noon UTC.

This talk is a lot less technical than previous ones I’ve given on this subject, which were aimed mainly at category theorists! You can watch it live on YouTube by going here or register to join via Zoom here.

Abstract. Category theory provides a general framework...

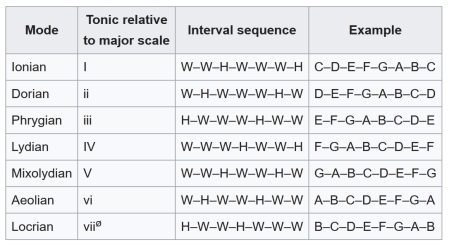
Modes (Part 1)

I’ve been away from my piano since September. I really miss playing it. So, I’ve been sublimating my desire to improvise on this instrument by finally learning a bunch of basic harmony theory, which I practice just by singing or whistling.

For example, I’m getting into modes. The following 7 modes are all obtained by taking the major scale and starting it at different points. But I find that’s not the good way for me to understand the individual flavor of each one.

Much better for me is to ...