Stirling’s formula says
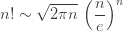
where  means that the ratio of the two quantities goes to
means that the ratio of the two quantities goes to  as
as 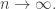
Where does this formula come from? In particular, how does the number  get involved? Where is the circle here?
get involved? Where is the circle here?
To understand these things, I think a nonrigorous argument that can be made rigorous is more useful than a rigorous proof with all the ε’s dotted and the δ’s crossed. It’s important, I think, to keep the argument short. So let me do that.
The punchline will be that the  comes from this formula:
comes from this formula:

...
Published on October 03, 2021 08:05
