Peter Smith's Blog, page 8
September 30, 2024
Three shorter book notes

Yuri Manin who died last year was a seriously distinguished mathematician, being — for instance — one of the first recipients of the Schock Prize for mathematics. His interests ranged very widely, from algebra and topology to quantum field theory. So A Course in Mathematical Logic for Mathematicians (1977 translation, Springer) is written by an author with an usually broad background which interestingly shows through from time to time in the book.
The Preface starts: “This book is above all addressed to mathematicians. It is intended to be a textbook of mathematical logic on a sophisticated level, presenting the reader with several of the most significant discoveries of the last ten or fifteen years. These include: the independence of the continuum hypothesis, the Diophantine nature of enumerable sets, the impossibility of finding an algorithmic solution for one or two old problems.” So, yes, this is indeed aimed at pretty competent mathematicians. And yes, the attraction of the book when it appeared was that it gave early textbook accounts of e.g. Boolean valued models in set theory, or of the MRDP theorem.
Almost fifty years on, there are — quite unsurprisingly — more accessible accounts to be had of those then-much-more-recent results. And the level of discussion can be, well, ‘sophisticated’. So Manin’s book isn’t, whether in whole or in part, really a candidate for primary recommendations in the Beginning Mathematical Logic Study Guide. Still, it is distinctive enough that it should probably get a mention as being of possible interest to enthusiasts who find its style congenial. Indeed, I thought it did get just such a mention in earlier versions of the Guide; but it turns out that my memory plays me false.

A book I do mention in the current Guide is Volume II of George Tourlakis’s Lectures, i.e. the volume on set theory (I was probably unnecessarily polite about it!). But what about Volume I (CUP, 2003)?
This has two long chapters. The first (204 pp.) is called ‘Basic Logic’. We get an account of first-order languages, a Hilbert-style proof system (with all instances of tautologies as axioms), soundness, completeness and compactness proofs, and a little model theory (including e.g. the Loś-Vaught test and something about infinitesimals). Then we learn about computability and recursive functions, leading to semantic and syntactic versions of the first incompleteness theorem. The menu of topics is a standard one, then. But I just can’t bring myself to warm to the way the exposition goes, especially when it comes to Gödelian incompleteness. There are, in summary terms, much better options available.
The second chapter (116 pp.) is called ‘The Second Incompleteness Theorem’. The blurb advertises this as “the first presentation of a complete proof of Gödel’s second incompleteness theorem since Hilbert and Bernay’s [sic] Grundlagen” (but cf. Adamowicz/Zbierski 1997?). To my mind, Tourlakis’s presentation hacks through a mass of detail in a way that isn’t going to engender much understanding at all. Stick e.g. to Rautenberg.

The third book I’m going to quickly mention and then mostly pass by is Harrie de Swart’s Philosophical and Mathematical Logic (Springer, 2018). This really is a strange mish-mash of a book, supposedly aimed at philosophers. There are chapters (not very good) on e.g. the philosophy of language and “fallacies and unfair discussion methods”, and e.g. a section on social choice theory. Then there are chapters more directly relevant to the Guide on propositional and predicate logic, modal logic and intuitionistic logic.
If the overall structure of the book is a bit of a disorderly hodgepodge, so too can be the structure of individual chapters. Take, for example, the chapter on propositional logic. We get a bit of baby-logic level talk about truth-functions, then suddenly a compactness argument. Then we are back to baby-logic on defining validity. A digression on enthymemes is followed by a bit of metalogic. We get a messily-presented Hilbert-style proof system. Then there is a digression on an underdescribed natural deduction system. Next we get signed tableaux and a completeness proof (but who would guess from de Swart’s presentation that these can be made beautifully elegant)? The chapter finishes with a random walk through some paradoxes, and then some arm-waving history in a strange chronology. What a mess!
And so it goes through other chapters, I think. So I mostly can’t like this book (and looking again at what I briefly said in the Guide before, I was too kind). Except — though I’ll want to double-check this — I can probably still recommend the chapter on intuitionism which I thought before gives a nice enough account of one way of doing tableaux for intuitionistic logic.
The post Three shorter book notes appeared first on Logic Matters.
September 29, 2024
“The best logic textbook ever”?

I was sorry to hear of the death a few days ago of Max Cresswell. In his long philosophical life he wrote widely, usually on logic-related topics. But for many of us he will always be most remembered as the co-author (with G. E Hughes) of that remarkable 1968 book An Introduction to Modal Logic. I’m ancient enough to remember buying it when it came out and being quite bowled over — not just by its then-still-shiny-new topic but by the book’s extraordinary lucidity and readability.
I’m not the only one with such memories: I see that in a comment on the Leiter blog, Allen Hazen has written “The original, 1968, Introduction to Modal Logic is perhaps the best logic textbook ever for its clarity and for explaining sophisticated technical concepts in ways a genuine beginner can follow.” And yes, we can surely agree that it must come high up any list of candidates for that prize — still a paradigm of what a logic textbook can be.
The post “The best logic textbook ever”? appeared first on Logic Matters.
September 27, 2024
Revisiting Cori & Lascar

I’m revisiting a number of older logic books with a view to seeing if/how they should feature in the new edition of the Study Guide. Next up, the text by René Cori and Daniel Lascar, whose French original was published in 1993, later translated in two parts as Mathematical Logic (OUP, 2000).
Its sub-title, “A Course with Exercises” highlights a very welcome feature of this text. The main bodies of the chapters in Part I add up to some 207 pages; there are in addition 31 pages of exercises and then, at the end of the Part I, no less than 85 pages of very well-presented solutions to the exercises. The proportions in Part II are similar. This means that even if you are using other texts as your main introductions to the various topics, you could profitably mine Cori and Lascar as a source of lots of worked exercises in a way that could be extremely useful, especially if you are largely teaching yourself logic from books.
What about the core presentations before you get to the exercises, though? Part I comprises four chapters. The first (46 pp. before the substantial set of exercises) is on the language and semantics of propositional logic, including a proof of the interpolation lemma and of compactness. The third (70 pp.) is on the language and semantics of predicate logic, with a little model theory. This is all highly respectable, though I wouldn’t recommend these pages as a first encounter — but you could safely add them to the long list of possible supplementary/consolidating readings, if their style appeals.
The fourth chapter (48 pp.) then very briskly introduces a proof-system for predicate logic (since this system counts as every instances of a tautology as an axiom, deleting the quantifier axioms and rules leaves us with a trivial and unilluminating proof system for propositional logic — evidently proof-theory isn’t the authors’ thing!). We then get a Henkin-style completeness proof, first for the case of finite/countable languages, and then for the general case appealing to Zorn’s Lemma, though the reader has to leap ahead to Part II of the book to find out what that lemma says. I didn’t find this to be particularly accessibly done, nor indeed are the following sections on Herbrand’s method and on resolution. There are better options out there.
What about the second chapter of Part I (43 pp.)? This is a stand-alone chapter which can be read independently or equally well can be skipped as far as following the rest of the book is concerned. You’ll need an amount of algebra and topology to follow this introduction to Boolean Algebra, which gets as far as the theorem that every Boolean algebra is isomorphic to the algebra of clopen subsets of its Stone space. Which strikes me as significantly more than the logical beginner really needs to know!
Moving on to Part II, there are again four chapters. The first of them (47 pp., still before the exercises) is on recursion theory and pretty clearly done, except that there is an unnecessarily non-standard characterization of a Turing machine. The next chapter (37 pp.) — after a little on representing recursive functions and on the arithmetization of syntax — gets us to versions of Gödel’s incompleteness theorems. Now, the detailed routes taken in the final sections — particularly to the second theorem — are not the most familiar ones. So it would be an interesting (and non-trivial) exercise for enthusiasts to work out quite how the arguments here relate to a conventional presentation as e.g. in my IGT. But this very thing which will therefore make the chapter interesting to those who already know a bit about incompleteness also makes it difficult to recommend it as a starting point for those new to the area.
The third chapter of Part II is on set theory (63 pp.). This is a more conventional treatment covering a conventional menu, and none the worse for that. We get the ZF axioms, and eventually Choice; meet the ordinals, transfinite induction, cardinals and their arithmetic, the axiom of foundation, and eventually inaccessibles and the reflection scheme. Indeed this does seem a particularly clear introduction at its level and scope of coverage.
The final chapter (50 pp.) is titled ‘Some model theory’. There is no default menu of topics for such a chapter. This one covers elementary substructures and the Tarski-Vaught test; something about the method of diagrams; more on interpolation and Beth’s definability theorem; ultraproducts and Łos’ theorem; some preservation theorems; the omitting types theorem; and a little more. All standard good things to know about, but perhaps — to my mind — not particularly excitingly done.
I won’t be rushing, then, to add special recommendations of Cori and Lascar to the next edition of the Study Guide, over and above the current recommendations of the exercises/solutions. But I will probably now mention the Gödel chapter and the sets chapter.
The post Revisiting Cori & Lascar appeared first on Logic Matters.
September 24, 2024
Boris Giltburg, Beethoven sonatas I
As an interlude in the oh-so-exciting cycle of posts on various logic books old and new, here’s one of my favourite pianists, Boris Giltburg, in the first concert of his new Beethoven cycle at Wigmore Hall.
He plays Sonata No. 1 in F minor Op. 2 No. 1 (starting at 8:30). Then Sonata No. 18 in E flat Op. 31 No. 3 “Hunt” (at 31:14) I. After the interval, Sonata No. 29 in B flat Op. 106 ‘Hammerklavier’ (at 59:27). Wonderful performances.
The post Boris Giltburg, Beethoven sonatas I appeared first on Logic Matters.
September 22, 2024
Skipping past five books …
I said at the end of the last post that I was going to return to discuss Smullyan’s Further Guide. But having looked at it again more closely, I’m inclined to think this book is really a bit too idiosyncratic to get more than a passing mention in the Logic Matters Study Guide. So on second thoughts I’ll say no more about it here. Which isn’t at all to deny that Smullyan’s book would be intriguing and challenging for the right reader.
One of the parts of the Study Guide I’m most concerned to improve in a second edition is the coverage of FOL; hence my (re)visiting a raft of relatively elementary texts to see what alternative/additional recommendations I might offer. Here, for the record, are three books which are broadly quite conventional and — looking back at some notes, and dipping in again — I simply judge to have nothing distinctive to recommend them in coverage and/or approach compared with other treatments of the same familiar material. Michał Walicki’s Introduction to Mathematical Logic (World Scientific, 2012, 268 pp.) is marred by bad English and is also unbalanced on PL vs FOL. Robert L Causey’s Logic, Sets and Recursion (Jones and Bartlett, 2nd edn. 2006, 512 pp.) strikes me as tedious. José Zalabardo’s Introduction to the Theory of Logic (Westview, 2000, 330 pp.) is better, but the technical presentations can be quite dense.

A level or two up from those three books, there is an earlier and more mathematically flavoured book by Zofia Adamowicz and Paweł Zbierski, Logic of Mathematics (Wiley 1977). This is a serious text; but it is often significantly harder work and less reader-friendly than many of the alternatives.
In a bit more detail, after a very brief introduction, the Logic of Mathematics has two parts. The first part (135 pp.) is an introduction to FOL, with an emphasis on model-theoretic ideas (so we start with discussions of mathematical structures, maps between structures, etc., before meeting first-order languages designed to talk about such things). There’s a standard axiomatic system, and a Henkin completeness proof. We get as far as defining ultraproducts and giving a direct proof of compactness using ultraproducts without going via completeness. All fine, but not distinctively inviting.
The second part of the book (105 pp.) starts with three chapters around and about the first incompleteness theorem, starting from a proof that the primitive recursive functions are representable in PA by 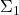 formulas. But this lovely topic is just not made as engaging as it should be. A fourth chapter then gives a decidedly opaque treatment of the second incompleteness theorem.
formulas. But this lovely topic is just not made as engaging as it should be. A fourth chapter then gives a decidedly opaque treatment of the second incompleteness theorem.
The book finishes with three ambitious chapters, one on the independence of Goodstein’s Theorem, one on Tarski’s result that the theory of ordered real closed fields admits the elimination of quantifiers and hence is complete, and one on Matiyasevich’s Theorem. Credit to Adamowicz and Zbierski for tackling these, but I can only report that in each case much more accessible discussions are available elsewhere.
True, these various negative headline judgements are rather peremptory; but then as I’ve said before the whole point of the Study Guide project is to make discriminations. So, moving on again, …
The post Skipping past five books … appeared first on Logic Matters.
September 19, 2024
Book note: Smullyan’s Guide

Ten years ago, when already in his ninety-fifth year, Raymond Smullyan published A Beginner’s Guide to Mathematical Logic (Dover, 2014), followed three years later by a sequel A Beginner’s Further Guide to Mathematical Logic (World Scientific, 2017).
I’m a huge admirer of Smullyan’s classic books (I mean, in particular, First-Order Logic and the trilogy starting with Gödel’s Incompleteness Theorems). His famed puzzle books are mightily ingenious too, though to be honest are not really so much to my own taste. Sometimes, as in his Logical Labyrinths, Smullyan mixes up the genres. But these late Guides are (relatively!) conventional in style, except for the way that significant problems (e.g. challenging you to prove theorems from hints) are scattered through the chapters, with detailed solutions at the end of chapters. The two books are aimed squarely at beginners, so should be most relevant to exactly those more elementary parts of my Beginning Mathematical Logic which most need revision. I didn’t say much about the books before, so I thought I should certainly take another more careful look, reminding myself what Smullyan covers and how.
Smullyan’s Beginner’s Guide is divided into four parts. Part I (57 pp.) is ‘General Background’ — something about sets, naively, but then pointers to the paradoxes; different infinite sizes of sets; mathematical induction; König’s Lemma; a generalized idea of compactness; and more. The sort of thing we want a beginning logician to know at some early stage; but these chapters are perhaps a little too idiosyncratic and uneven in level and coverage to be the recommended source.
Part II (68 pp.) is on ‘Propositional Logic’. Ch. 5 introduces truth-tables and tautologies in a gentle and elementary way. Ch. 6 is, by contrast, a rather fast-track introduction to propositional tableaux — in just twenty pages we get signed and unsigned tableau, Smullyan’s unified notation, soundness and completeness proofs, a compactness proof, and even dual tableaux. Ch. 7 introduces a familiar sort of system of axiomatic propositional logic K (closely akin to Kleene’s, with four built-in connectives taken as primitive). The chapter then takes an unusual turn: it is shown that K is equivalent to a very unfamiliar axiomatic system U, and then that every propositional tableau proof can be turned into a U-proof, showing that K is complete for the usual two-valued semantics.
Part III is on ‘First-Order Logic’ (36 pp). Ch. 8 introduces the language of FOL, syntax and semantics, and an axiomatic system in just ten pages before the solutions to examples start — which will be surely too rushed for those who have not previous encountered a treatment. The brisk Ch. 9 is on tableaux for FOL, completeness, compactness, (downward) Löwenheim-Skolem, and more — again all very speedy.
In sum, I think Parts II and III are too uneven and in places too rushed to make for a recommendable first introduction to PL and FOL. Chapters 6 and 9 could, though, make a usable introduction to the tableaux approach to those already familiar with other versions of PL/FOL — though I do think there are rather better options at different levels.
Part IV, however, strikes me as working very well, the high point of the book. The topic is ‘The Incompleteness Phenomenon’. The five chapters proceed from quite abstract versions of Gödel and Tarski — harking right back to Smullyan’s landmark 1959 paper ‘Languages in which self reference is possible’ — through to gradually more concrete semantic and syntactic versions of the first incompleteness theorems, reaching Peano Arithmetic in the penultimate chapter, with the second theorem and some related topics in the final chapter.
This is all done with over half a century of polish, with Smullyan setting more or less teasing problems as he goes along. These outstanding chapters will indeed make a quite excellent counterpoint to the more conventional, concrete-first, treatments of Gödel and Tarski, and will certainly deepen understanding. To be warmly recommended.
(I’ll discuss the Further Guide in a later post.)
The post Book note: Smullyan’s Guide appeared first on Logic Matters.
September 17, 2024
Book note: Three Views of Logic

I hadn’t heard of Three Views of Logic by Donald W. Loveland, Richard E. Hodel, and S.G. Sterrett (Princeton UP, 2013) until it was brought to my attention quite recently. I thought I should take a look at this book for two main reasons. First, it is aimed at beginners, hence at possible readers of the Study Guide: “Demonstrating the different roles that logic plays in the disciplines of computer science, mathematics, and philosophy, this concise undergraduate textbook covers select topics from three different areas of logic: proof theory, computability theory, and nonclassical logic.” Second, one of the authors has already written a widely admired textbook on mathematical logic.
The three parts of this book are written quite separately and are of very different characters. The longest and by far the best part (125 pp.) is by Hodel, and provides a conventional, well-written, very accessible introduction to computability theory. To be honest, I’m not sure the world really needed yet another one; but this can certainly be recommended, even though — as I’ll note in a moment — it stops in an unsatisfyingly abrupt way.
We start with a very clear informal introduction to ideas of algorithms, computability, decidability, semi-decidability etc. Then we meet one machine model of computability in terms of register machines, leading up to showing the the decision problem for FOL is unsolvable as is Thue’s word problem.
Next we get a mathematical account of computability in terms of recursive functions, and a proof that these are RM-computable, before going on to isolate the primitive recursive functions, introduce Kleene’s T-predicate, and the idea of Gödel-coding, preparing for a proof that all the RM-computable functions are recursive.
So far, so good! Everything is going quite swimmingly until Hodel (I guess) hits his page limit, and we get a very rushed couple of pages on incompleteness and the story is then perhaps rather annoyingly left hanging, with a pointer to its continuation in his earlier An Introduction to Mathematical Logic.
What about the other two parts of book? You can/should certainly ignore Loveland’s contribution, a presentation (92 pp.) of propositional and predicate logic using a resolution system: this is not done well, and there are much clearer accounts to be found elsewhere. (You would grimace, too, at his opening confusion concerning the regimentation of ‘so’ or ‘therefore’, about which the less said the better.)
The last part of the book (pp. 94) is an account of one brand of relevance logic. I’m highly resistant to the supposed charm of such deviations from mainstream logic. And fifty years after Anderson and Belnap (the heroes here) wrote — as some of us would say, muddying the waters about the difference between bare conditional claims and claims about stronger implication relations — and after fifty years of insightful work on conditionals, I don’t find their approach, pretty uncritically rehearsed by Sterrett, any more persuasive. But OK, suppose we do want to explore down that rabbit-hole. Then to be fair, Sterrett unfolds the story pretty clearly: some might indeed find this helpful.
Equally, however, as epicycles get piled up, e.g. complicating the intuitive elegance of a Fitch-style deductive system, the project — for most sensible readers! — will seem increasingly unattractive. After all, formalizing a logical system is a cost-benefit game, as we reap the benefits of a simple, easy to handle, systematizion of some inferential practice at the costs of collapsing some distinctions we might want to preserve in other contexts and generating some initially unintuitive results at the margins. The classical logician aiming to regiment standard mathematical reasoning, faced with Sterrett’s non-classical alternative, will judge that the supposed benefits aren’t worth the cost. But there it is.
The post Book note: Three Views of Logic appeared first on Logic Matters.
September 16, 2024
La vera Zerlina, la vera Susanna
Five minutes of delight … Giulia Semenzato singing ‘Batti, batti, o bel Masetto’ from Don Giovanni. She makes a wonderful Zerlina in that concert performance of the aria.
Semenzato brings the same feistiness, the same tenderness, and the same wonderful voice to her performance of Susanna in The Marriage of Figaro at the Royal Opera House a couple of years ago. She is just terrific in the role — exactly my idea of Susanna — and the whole production is hugely enjoyable. So, when you have a free evening, you can watch the complete opera here — and indeed it is an amazing bargain to subscribe to the ROH for a month. Very, very warmly recommended!
The post La vera Zerlina, la vera Susanna appeared first on Logic Matters.
September 15, 2024
Book note: Kaye, The Mathematics of Logic

Richard Kaye’s The Mathematics of Logic (CUP, 2007) is subtitled ‘A guide to completeness theorems and their application’. This is an unconventional — one might even say idiosyncratic — introduction to first-order-logic and related themes. Some will appreciate it as a somewhat bumpy but illuminating ride: but probably most will prefer a more conventional text for a first encounter with FOL.
There are a dozen chapters, each comprising a main section (which should be accessible to undergraduates), followed by a section of examples and exercises, followed by one or sometimes two optional starred sections which can require more mathematical background (in some cases, graduate level). I’ll return to those optional sections later; but let’s concentrate first on the main sections together with their amplifying sections of examples and exercises. These make for a core book of under 140 pages. So how does the story go?
Ch. 1 is on König’s Lemma (initially for binary trees). Why start here? The idea is that we have two relevant ideas of infinity for such trees, (i) a ‘definition from perfect information’, where we take a god’s eye view of the whole tree and say it is infinite if it has an infinite number of nodes, and (ii) a ‘definition from imperfect information’, where we take the view of, as it were, an ant who can’t see the whole tree but is crawling along a path, who says the tree is infinite if it has an unending path. We then have a ‘soundness’ proof (trivial) and a ‘completeness’ proof (König’s Lemma) which tell us that for binary trees the two definitions of an infinite tree come to the same. Kaye’s suggestion is that this provides an analogue for the soundness and completeness proofs that will concern us later, relating semantic definitions of validity (which are definitions from perfect information, surveying all models) and syntactic definitions (it is enough to have imperfect information, just one particular proof). Or so goes the story.
Ch. 2 is on posets and Zorn’s Lemma. We know that at some point, when it comes to a strong completeness theorem for FOL with an uncountable language we’ll need Zorn’s Lemma or an equivalent. This chapter provides a pretty clear introduction.
Ch. 3 introduces a toy formal system with simple rules for deriving finite binary strings from an initial set of such strings. We get some illustrative syntactic reasoning about what can and can’t be derived by manipulations in the system. And then we meet an interpretation of the formalism in terms of infinite paths in binary trees, and find proofs of corresponding soundness and completeness theorems. Ch. 4 gives us another toy system, this time with a reductio rule (and we get a Fitch-style plan for laying out reductio derivations). This time the associated interpretation is to do with posets. So these two chapters aim to introduce both some proof-theoretic and semantic ideas in particularly simple contexts. These chapters could work rather well for some readers.
Ch. 5 tells us a little about those posets which are lattices and then introduces Boolean algebras.
With those preliminaries in place, we reach the core of the book. First, Ch. 6 introduces (clearly though rather rapidly?) a Fitch-style proof system for propositional logic. And Ch. 7 treats semantics, though — rather unusually — semantic consequence is officially defined from the start in terms of valuations over all Boolean algebras. It is then proved as a result that this notion is equivalent to the usual one defined in terms of two-valued interpretations. (But we miss the usual idea that two-valued interpretation gives the sense of the connectives.)
Ch. 8 is more on the algebraic theory of Boolean algebras, filters and ideals etc.: the main result is the Boolean Prime Ideal Theorem. (Though this chapter probably could/should be skipped on a first reading).
Then we get to FOL. Ch. 9 introduces the language of first-order logic with identity, and gives a Fitch-style proof-system. I think this would all be too quickly done if you’d really never encountered either a careful treatment of the language or a proof system for quantified logic before. There is only an incomplete gesture towards a semantic story too — note in particular this remark:
If an L-formula
has free variables, these variables must be given some meaning or interpretation in an L-structure M before we can say what it means for
. In other words, these free variables should be replaced by constant symbols or closed terms with specific meaning in M. However, if some meaning is defined or understood for these variables, and we are arguing in an informal sense rather than a picky and pedantic way, we can use this understood meaning to make sense of
for such formulas
too.
So Kaye doesn’t spell out the usual Tarksian semantics built on its picky and pedantic account of how to handle open wffs. Then Ch. 10 gives us a Henkin-style proof via Zorn’s Lemma that if 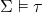 , where
, where  is a set of sentences and
is a set of sentences and 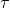 is a sentence, then
is a sentence, then 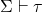 (so those familiar with more standard presentation will want to work out just how Kaye can do this while not having spelt out a Tarskian semantics).
(so those familiar with more standard presentation will want to work out just how Kaye can do this while not having spelt out a Tarskian semantics).
Ch. 11, after introducing the notion of countability, shows that in a countable language a consistent set of sentences will have a countable model. It then proves an upward L-S theorem, and takes a first look at ideas like 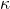 -categoricity, mentioning Morley’s theorem. Finally, Ch. 12 briefly but clearly discusses non-standard analysis.
-categoricity, mentioning Morley’s theorem. Finally, Ch. 12 briefly but clearly discusses non-standard analysis.
Overall, this core of Kaye’s book could certainly make for interesting supplementary reading for someone starting out on FOL, casting light on some key ideas from somewhat unusual directions. But I don’t think it is mere conservatism that would make me reluctant to recommend anyone starting here.
The starred sections which end every chapter are of varying levels of difficulty/sophistication, but almost all are interesting. In particular, Ch. 2 adds a section saying more about Choice and Zorn’s Lemma, making this chapter a useful resource. Ch. 7 adds a little about complexity, P and NP, just enough to whet the reader’s appetite for more. Ch. 10 has two additional sections, one on compactness in logic and topology, and another (quite substantial) on omitting types. The last section of Ch. 12 continues the story about non-standard analysis in an illuminating way. (Some readers dipping into the book might like to start with the starred sections which catch their eye, and backtrack as necessary into the relevant preceding chapters.)
The post Book note: Kaye, The Mathematics of Logic appeared first on Logic Matters.
September 13, 2024
New: Journal for the Philosophy of Mathematics

The first issue is now out of a new open-access publication, the Journal for the Philosophy of Mathematics, started up under the auspices of the European Society for the Philosophy of Mathematics.
This seems a promising development. There is a lot of interesting work going on in the area, and only limited space in the often excellent Philosophia Mathematica. The editorial team is terrific.
The initial issue is a set of invited papers (mostly by rather familiar authors) with the aim, the editor writes, of “showcas[ing] the quality and diversity that we are looking for in our future articles and volumes. Now that the standards have been set, we proudly open the JPM for submissions from philosophers of mathematics everywhere.” To mark your card, I’d say the invited papers by Enayat & Łełyk, Hamkins, Shapiro, and Soysal are the four really worth delving into here.
I look forward to seeing how the journal develops.
The post New: Journal for the Philosophy of Mathematics appeared first on Logic Matters.



