Peter Smith's Blog, page 10
August 25, 2024
Schubert on Sunday 9: Elias Quartet play D. 804
The last Schubert on Sunday post — over six months ago, how did that happen? — was a wonderful video recording of Julian Prégardien singing Die Schöne Mullerin, accompanied by the fortepianist Els Biesemans. Prégardien has now just released a CD of the same cycle, this time with the fortepianist Kristian Bezuidenhout. This is quite remarkable too, as Bezuidenhout brings out all the colour-range of his Graf-style instrument: but there is still something quite especially moving about the filmed live recording before a small audience, with Els Biesemans herself obviously so intensely wrapped up in the music as the cycle reaches it end.
Of Schubert’s late quartets, the Rosamunde D. 804 is about my favourite — except, of course, on the days when it is Death and the Maiden or the great G major quartet! Anyway, here are the Elias Quartet, rightly Wigmore Hall favourites, in an elegiac performance.
The post Schubert on Sunday 9: Elias Quartet play D. 804 appeared first on Logic Matters.
August 24, 2024
Book note: Halbeisen & Krapf, Gödel’s Theorems and Zermelo’s Axioms

A standard menu for a first mathematical logic course might be something like this: (1) A treatment of the syntax and semantics of FOL, presenting a proof system or two, leading up to a proof of a Gödel’s completeness theorem (and then a glance at e.g. the compactness theorem and some initial implications). (2) An introduction to formal arithmetic, a little about computability, with Gödel’s incompleteness theorems a highlight. (3) A modest amount of set theory, looking e.g. at the way number systems including the reals can be constructed in set theory; a first encounter with cardinals, ordinals and Choice; then the formalization of set theory in ZFC. With all this leading to an emerging sense of (4) the limitations of first-order theories and the ubiquity of non-standard models.
So an attractive, accessible, relatively short, book covering Gödel’s Theorems (completeness/incompleteness) and Zermelo’s Axioms (and why we need a bit more than Zermelo’s original proposals) could indeed have a grateful readership.
But Lorenz Halbeisen and Regula Krapf’s promisingly titled book (published by Birkhäuser in 2020) is not that book. It does tick the box of being relatively short (x + 236 pp.). However — to be blunt about it — this is not particularly reader-friendly, often unnecessarily hard going, and there are much better options, particularly for self-study.
Part I introduces FOL, initially in Hilbert-style (with a selection of axioms presented in a take-it-or-leave-it spirit). Then we get what is advertised as a natural deduction system, though by p. 24 it is beginning to look more like a sequent calculus (in a way that could confuse the reader). On p. 30 we get a trivial syntactic result labelled as the compactness theorem (in a way that could again confuse the reader who was seen standard talk of compactness elsewhere). Then we get a pretty messy introduction to the semantics of FOL.
Part II proves the completeness theorem (for countable signatures), done Henkin-style. Somehow the rather neat elegance that such proofs can have is quite lost in the telling: would the student new to this come away with a good sense of the fundamental ideas? — I doubt it.
Part III starts with a short chapter on standard and non-standard models of PA, before actually looking in the next chapter at how arithmetic can be done in PA. There follows a twenty-page chapter hacking through the arithmetization of syntax for PA: ok, this is necessarily a messy business, but it is certainly done more accessibly and more attractively elsewhere.
Then we get the key chapter on the first incompleteness theorem. Once more, I can’t say that this is done in a reader-friendly way. The diagonalization lemma is plucked out of the sky; and there’s careless talk of the kind we warn our students against — the lemma “allows us to make self-referential statements, i.e. for a formula  with one free variable it provides a sentence
with one free variable it provides a sentence 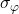 which states ‘I have the property
which states ‘I have the property  ’. ” No it doesn’t. And then the initial proof of incompleteness on p. 112 will puzzle readers who’ve seen (or are about to see) other presentations — how do we get that PA doesn’t prove a fixed point of
’. ” No it doesn’t. And then the initial proof of incompleteness on p. 112 will puzzle readers who’ve seen (or are about to see) other presentations — how do we get that PA doesn’t prove a fixed point of 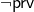 without mentioning
without mentioning  -consistency?
-consistency?
Moving on, we do get a full-dress eight-page proof of the second incompleteness theorem for PA, and in particular of the third derivability condition, i.e. it’s shown that PA proves 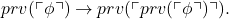 It probably sounds ungrateful, but is this really what we want or need in an introductory book? Only if particularly nicely done, which it isn’t.
It probably sounds ungrateful, but is this really what we want or need in an introductory book? Only if particularly nicely done, which it isn’t.
Part IV is on set theory, starting with a twenty page chapter on the axioms of ZFC, but also explaining the set-theoretic definitions of functions and relations, saying something about Choice, and introducing ordinals and cardinals. All surely far too fast for the student for whom this really is all new.
The remaining chapters are on models of set theory, standard and non-standard; on ultrafilters and ultra products (and so completeness for FOL with uncountable signatures); briefly again on non-standard models of PA; and then on real numbers, non-standard models of the reals, and a little on non-standard analysis. My sense is that these final chapters — which are worthwhile reading for someone who has got the basics nailed down elsewhere — is where the authors’ real interest lies.
So my summary recommendation: you can cheerfully ignore what’s gone before (there are many better options for introducing their material), but students with enough background might well find the last four chapters, some 50 pages, interesting and profitable.
The post Book note: Halbeisen & Krapf, Gödel’s Theorems and Zermelo’s Axioms appeared first on Logic Matters.
August 22, 2024
Book note: Westerståhl, Foundations of Logic, III & IV
 There are, of course, oodles of books introducing FOL (and maybe covering a lot more). However, for one reason or another, many respectable texts on FOL can be difficult to recommend very warmly for self-study (over-doing the “rigour”, under-doing the motivational chat, choosing a horrible deductive proof system, etc., etc.). Against this background, the first two parts of Foundations of Logic do seem to me to stand out as providing a particularly attractive option.
There are, of course, oodles of books introducing FOL (and maybe covering a lot more). However, for one reason or another, many respectable texts on FOL can be difficult to recommend very warmly for self-study (over-doing the “rigour”, under-doing the motivational chat, choosing a horrible deductive proof system, etc., etc.). Against this background, the first two parts of Foundations of Logic do seem to me to stand out as providing a particularly attractive option.
Again, there are many more books which introduce formal arithmetic, incompleteness, and some entry-level computability theory. But this time, we are already rather generously supplied with a number of particularly accessible and enjoyable options taking varying paths through the material; and I’m not sure that Parts III and IV of Westerstähl’s book trump the alternatives. Which is not to deny that the book continues to be very attractively written, well-organized with a lot of signposting. In particular, Westerståhl does a very good job in signalling what are the Big Ideas, and what is the hack work required to confirm that e.g. primitive recursive functions are representable in PA, or that syntax is sufficiently arithmetizable, etc. It then becomes a judgment call just how many of the tedious under-the-bonnet details you really need to go into.
In fact, the particular path to the incompleteness results that Westerståhl takes closely resembles the one in my own IGT (which gets a friendly mention in his preface). But at various points he goes into more of the nitty-gritty detail than I do — more, obviously enough, than I judged was necessary. And, despite the signposting, I can well imagine some student readers losing orientation. So (what a surprise!) if you want to follow this path to Gödel’s Theorems — and there are alternatives — I’d still recommend starting with IGT for self-study. Westerståhl’s Parts III and IV would then make for quite excellent follow-up reading to consolidate understanding.
In just a little more detail, Part III (‘Incompleteness’) comprises six chapters. Ch. 7 is a very nice chapter, outlining what is to come — and indeed could be read stand-alone for preliminary orientation on incompleteness and computability, whatever you go on to read as your main text(s). Ch. 8 is about primitive recursive functions. Ch. 9 introduces first-order Peano Arithmetic. Ch. 10 establishes the representability of p.r. functions. Ch. 11 is on the arithmetization of syntax. So far so good, if sometimes unnecessarily detailed? Then, the target of this Part, Ch. 12 is a distinctly action-packed, indeed over-busy, forty-page chapter on incompleteness (IGT takes over twice as many pages covering much of the same material as in this chapter, and I really think is all the better for it).
Part IV (‘Computability’) has three chapters. Ch. 13 is on Turing machines, recursive functions and decidability. Ch. 14 is on undecidability of extensions of PA, of FOL, of the halting problem (so these two chapters correspond to the much of final half-dozen chapters of IGT). And then Ch. 15 dips its toes into computability theory (occasionally going rather beyond anything in IGT, e.g. in introducing the s-m-n theorem, creative sets, etc.). All good stuff, and I should certainly note that the end-of-chapter Exercises — as earlier in the book — continue to be really excellent.
But, as I say, these Parts wouldn’t be my recommended first entry-point for self-study of this material. However, those who would prefer a somewhat faster trek along much the same path as IGT with a few extra sights along the way will find Westerståhl’s book a very admirable guide.
The post Book note: Westerståhl, Foundations of Logic, III & IV appeared first on Logic Matters.
August 21, 2024
Book note: Westerståhl, Foundations of Logic, I & II
 Dag Westerståhl’s Foundations of Logic: Completeness, Incompleteness, Computability is, by some margin, the most attractively written book at its level that I have newly encountered for some years.
Dag Westerståhl’s Foundations of Logic: Completeness, Incompleteness, Computability is, by some margin, the most attractively written book at its level that I have newly encountered for some years.
The book is based on lecture courses give at Stockholm University and latterly at Tsinghua University, Beijing, and evidently reflects long teaching experience. Especially in the first two Parts of the book, the expositional choices are very well-judged, and the balance between motivational chat and worked-through formal details seems just right to me. Many student readers should find this book quite excellent for self-study. (Long-time readers of this blog will know that I’m not exactly over-quick to heap praise like this!)
The book was published by CSLI (distributed by the University of Chicago Press) in January 2024, ISBN 978-1684000005. You should certainly warmly recommend it to your local university or college library. For some reason, Amazon and others quite mis-report the page length as 80pp.: in fact it is xiv + 451 pages, so the printed paperback price (§45, £36 from Waterstones) is by current standards pretty reasonable. Though, as we will see, it is a great pity that the author seems not to have come to an arrangement which makes the PDF freely downloadable.
In just a little more detail, Part I (‘Background’, 78 pp.), introduces propositional and FOL languages, and the idea of interpretations and semantic consequences, and then gives both a natural deduction proof system (Gentzen-style) and a Hilbert proof system. Part II (‘Completeness’, 80 pp.) gives soundness and completeness theorems for propositional logic and FOL, and then there is a chapter on the L-S theorems, compactness, and a smidgin of model theory. Part III (‘Incompleteness’, 134 pp.) discusses primitive recursive functions and their representability, Peano arithmetic, arithmetization, and Gödel’s Theorems. Part IV (‘Computability’, 114 pp.) adds chapters on decidability, undecidability and a modest amount more computability theory. There is an Appendix (34 pp.) on sets and functions, etc., for those that need it.
So this is a very substantial book. But Parts I and II in particular strike me as admirably well-paced, to my mind neither over-packed with detail, nor tediously slow-moving.
In the rest of this post, I’ll say just a little more about Parts I and II. Then I’ll follow up with a later post on Parts III and IV.
After an inviting, reader-friendly, Introduction (Ch. 1), Part I has two substantial chapters, the first one (Ch. 2) introducing the syntax and semantics of propositional logic and then of FOL. This is done conventionally, in that we get the usual Tarski-style story, with the semantics done via assignments of objects to all variables at once in the usual way, interpreting wffs with free variables. So, in the usual way, we need slightly messy stories about allowable substitutions avoiding variable-capture, slightly messy notation for handling assignments to variables, etc. However, this is all expounded particularly clearly, with motivations at various points very well explained. (There’s perhaps just a hint in §3.2 that we could do things differently, in the way I myself would prefer, using a supply of constants-as-parameters, rather than making variables do double duty — and then we can assign parameters temporary interpretations one at a time, just on an as-needed basis. But I can of course see the virtues of sticking to the conventional Tarskian line.)
Then Ch. 3 introduces two proof systems, Gentzen-style natural deduction and a minimalist, two-connective, Hilbert-style system. I think I would probably have spent just two or three more pages giving more examples of Gentzen-style proofs, showing tactics for building up proof-trees in natural ways (to re-inforce the advertised claim that this really is a natural deduction system). But still, this is again all very well done, with possible stumbling blocks — e.g. the use of vacuous discharge — nicely elucidated. The chapter finishes particularly helpfully with an outline proof that the two proof systems march in step, warranting the same deductions.
Part II begins with a short chapter (Ch. 4) proving the completeness of the Hilbert proof system for propositional logic, using maximal consistent sets and Lindenbaum’s Lemma. As in previous (and future!) chapters, there are excellent exercises, including in this case ones exploring another completeness proof and presenting the interpolation lemma for PL. Then, closely following that chapter’s overall structure, we get a short chapter (Ch.5) proving the completeness theorem for FOL using Henkin’s method — very sensibly doing the proof for FOL without identity first, before in the final section of chapter complicating the story to handle identity. I wonder if that last section is just a bit denser than it needs to be — but overall, again, this seems quite excellently well done.
The rest of Part II concludes with a significantly longer chapter (Ch. 6) titled, simply, ‘Model theory’. The first eight sections introduce a handful of predictable entry-level topics: more ideas about structures, about isomorphisms between structures, notions of definability, the compactness theorem (as a corollary of completeness) and some of its applications, and the Löwenheim-Skolem theorems. The remaining sections are more challenging, and could well be skipped on a first reading. §6.9 reflects Westerstähl’s interest in generalized quantifiers and quantifiers in natural language. §6.10 is on Ehrenfeucht–Fraïssé games. §6.11, ambitiously, is on Lindström’s Theorem.
Suppose we stop before those last three sections (though take in the still-relevant end-of chapter exercises). Then what we have before us is a book-within-a-book, Westerståhl’s 150 page introduction to FOL that is, I think, particularly attractively written and accessible. It takes its place among the best options for self-study.
The post Book note: Westerståhl, Foundations of Logic, I & II appeared first on Logic Matters.
Book note: Westerstähl, Foundations of Logic, I & II
 Dag Westerstähl’s Foundations of Logic: Completeness, Incompleteness, Computability is, by some margin, the most attractively written book at its level that I have newly encountered for some years.
Dag Westerstähl’s Foundations of Logic: Completeness, Incompleteness, Computability is, by some margin, the most attractively written book at its level that I have newly encountered for some years.
The book is based on lecture courses give at Stockholm University and latterly at Tsinghua University, Beijing, and evidently reflects long teaching experience. The expositional choices are very well-judged, and the balance between motivational chat and worked-through formal details seems just right to me. Many student readers should find this book quite excellent for self-study. (Long-time readers of this blog will know that I’m not exactly over-quick to heap praise like this!)
The book was published by CSLI (distributed by the University of Chicago Press) in January 2024, ISBN 978-1684000005. You should certainly warmly recommend it to your local university or college library. For some reason, Amazon and others quite mis-report the page length as 80pp.: in fact it is xiv + 451 pages, so the printed paperback price (§45, £36 from Waterstones) is by current standards pretty reasonable. Though, as we will see, it is a great pity that the author seems not to have come to an arrangement which makes the PDF freely downloadable.
In just a little more detail, Part I (‘Background’, 78 pp.), introduces propositional and FOL languages, and the idea of interpretations and semantic consequences, and then gives both a natural deduction proof system (Gentzen-style) and a Hilbert proof system. Part II (‘Completeness’, 80 pp.) gives soundness and completeness theorems for propositional logic and FOL, and then there is a chapter on the L-S theorems, compactness, and a smidgin of model theory. Part III (‘Incompleteness’, 134 pp.) discusses primitive recursive functions and their representability, Peano arithmetic, arithmetization, and Gödel’s Theorems. Part IV (‘Computability’, 114 pp.) adds chapters on decidability, undecidability and a modest amount more computability theory. There is an Appendix (34 pp.) on sets and functions, etc., for those that need it.
So this is a very substantial book. But it strikes me as admirably well-paced, to my mind neither over-packed with detail, nor tediously slow-moving.
In the rest of this post, I’ll say just a little more about Parts I and II. Then I’ll follow up with a later post on Parts III and IV.
After an inviting, reader-friendly, Introduction (Ch. 1), Part I has two substantial chapters, the first one (Ch. 2) introducing the syntax and semantics of propositional logic and then of FOL. This is done conventionally, in that we get the usual Tarski-style story, with the semantics done via assignments of objects to all variables at once in the usual way, interpreting wffs with free variables. So, in the usual way, we need slightly messy stories about allowable substitutions avoiding variable-capture, slightly messy notation for handling assignments to variables, etc. However, this is all expounded particularly clearly, with motivations at various points very well explained. (There’s perhaps just a hint in §3.2 that we could do things differently, in the way I myself would prefer, using a supply of constants-as-parameters, rather than making variables do double duty — and then we can assign parameters temporary interpretations one at a time, just on an as-needed basis. But I can of course see the virtues of sticking to the conventional Tarskian line.)
Then Ch. 3 introduces two proof systems, Gentzen-style natural deduction and a minimalist, two-connective, Hilbert-style system. I think I would probably have spent just two or three more pages giving more examples of Gentzen-style proofs, showing tactics for building up proof-trees in natural ways (to re-inforce the advertised claim that this really is a natural deduction system). But still, this is again all very well done, with possible stumbling blocks — e.g. the use of vacuous discharge — nicely elucidated. The chapter finishes particularly helpfully with an outline proof that the two proof systems march in step, warranting the same deductions.
Part II begins with a short chapter (Ch. 4) proving the completeness of the Hilbert proof system for propositional logic, using maximal consistent sets and Lindenbaum’s Lemma. As in previous (and future!) chapters, there are excellent exercises, including in this case ones exploring another completeness proof and presenting the interpolation lemma for PL. Then, closely following that chapter’s overall structure, we get a short chapter (Ch.5) proving the completeness theorem for FOL using Henkin’s method — very sensibly doing the proof for FOL without identity first, before in the final section of chapter complicating the story to handle identity. I wonder if that last section is just a bit denser than it needs to be — but overall, again, this seems quite excellently well done.
The rest of Part II concludes with a significantly longer chapter (Ch. 6) titled, simply, ‘Model theory’. The first eight sections introduce a handful of predictable entry-level topics: more ideas about structures, about isomorphisms between structures, notions of definability, the compactness theorem (as a corollary of completeness) and some of its applications, and the Löwenheim-Skolem theorems. The remaining sections are more challenging, and could well be skipped on a first reading. §6.9 reflects Westerstähl’s interest in generalized quantifiers and quantifiers in natural language. §6.10 is on Ehrenfeucht–Fraïssé games. §6.11, ambitiously, is on Lindström’s Theorem.
Suppose we stop before those last three sections (though take in the still-relevant end-of chapter exercises). Then what we have before us is a book-within-a-book, a 150 page introduction to FOL that is, I think, particularly attractively written and accessible. It takes its place among the best options for self-study.
The post Book note: Westerstähl, Foundations of Logic, I & II appeared first on Logic Matters.
August 19, 2024
Book note: Moerdijk & van Oosten, Sets, Models and Proofs
Back (slowly, slowly) to logical matters. My plan for the rest of the year is to put together a second edition of what is consistently the most downloaded of the Big Red Logic Books (and also, surprisingly, the second-best paperback seller), namely Beginning Mathematical Logic: A Study Guide. It won’t be a radical revision, though I particularly want to improve the early chapter on FOL (expanding the overview, and moving the ensuing multi-recommendations into a separate chapter), and I need to write a proper chapter on type theories which I really skimped on before.
Over the coming weeks, then, as I take a look at some recent (or not so recent books) which are candidates for being newly mentioned in the Guide, I’ll post some book notes here, mostly as aides-memoire for myself. And hearing at my back time’s wingèd chariot hurrying near, I’ll probably be brisker and perhaps less patient than in the past. Make of such notes what you will.
 I did, for example, quickly become impatient with this really rather odd book. Ieke Moerdijk and Jaap van Oosten’s Sets, Models and Proofs (Springer, 2018) is just 113 pages long, before we get to the Appendix on ‘Topic for Further Study’. You might well predict that, in such a short compass, none of the announced three big topics can possibly be dealt with both accessibly and in enough detail to make a particularly useful text. You’d be right.
I did, for example, quickly become impatient with this really rather odd book. Ieke Moerdijk and Jaap van Oosten’s Sets, Models and Proofs (Springer, 2018) is just 113 pages long, before we get to the Appendix on ‘Topic for Further Study’. You might well predict that, in such a short compass, none of the announced three big topics can possibly be dealt with both accessibly and in enough detail to make a particularly useful text. You’d be right.
Chapter 1 (36 pp.) is titled, simply, ‘Sets’. The aim is “to develop your understanding of sets beyond the use you have made of them in your first years of mathematics.” So we get, in short order, §1 on cardinal numbers and Schröder–Cantor–Bernstein, §2 on the Axiom of Choice, §3 on posets and Zorn’s Lemma and cardinal comparability, §4 on well-ordered sets and transfinite recursion, and §5 on equivalents to Choice. OK, that’s a perfectly sensible menu of topics to offer those who already have a secure grip on e.g. most of the introductory chapter on sets in Munkres’s topology book or the equivalent. But to my mind, the exposition just isn’t that reader-friendly compared with alternatives elsewhere, such as Enderton’s book. Certainly not a top recommendation.
And there is another point. Here’s the offered definition of AC:
The Axiom of Choice is the assertion that for every surjective function
there exists a “section”; that is, a function
such that
for each
.
You’ll recognize that as the preferred categorial characterisation of choice. And no surprise there: Moerdijk and van Oosten are category theorists. And more generally, their story unfolds not as a about sets but as about sets and the morphisms between them: so functions are served up as sui generis items (and likewise, cardinal numbers in this chapter seem to be treated as sui generic objects, not explicitly identified as themselves sets). Now, in one way I’m all for this. It arguably does go with our “understanding of sets” as actually used in elementary, non-set-theoretical, mathematics (cf. Leinster’s well-known piece on rethinking set theory). However I don’t think it is best policy to proceed this way quite unannounced, in a way which could potentially puzzle the more reflective student who has been told (rightly or wrongly) that functions are sets, or who has met more conventional definitions of AC and wonders why the given one here is chosen.
Chapter 2 (43 pp.) is on ‘Models’. §1 is a preliminary section on the language of ring theory. Then §2 introduces first-order languages, and §3 is on structures for first-order languages and notions of validity and equivalence. §4 gives examples of languages and structures (for graphs, rings, vector spaces, etc.). The authors prefer the approach to semantics of a language L which adds to L a fixed constant for every object in the domain (rather than going via assignments of values to variables, or adding new temporary names for objects as needed); but there’s no discussion of why we need some such approach. Again I can only report that by my lights this basic stuff isn’t done in an especially user-friendly way; I wouldn’t recommend these compressed sections as a starting-point for self-study.
§5 is on compactness. And this is actually quite nicely done. You could give this to a student who has previously met the compactness theorem as an easy corollary of the completeness theorem, (a) to provide revision on some of the elementary implications of compactness, and then (b) to display a purely semantic proof of compactness using ultrafilters.
Following on §6 is on substructures and elementary substructures, §7 is on quantifier elimination, §8 is on the Löwenheim-Skolem theorems, and 9 deals with categorical theories. All good topics — but in just 17 pages? These sections could provide useful revision material, I guess, but are again surely not the place to start. Still, Chapter 2 §§5–8 is the best bit of the book.
Chapter 3 (22 pp.) discusses ‘Proofs’. §1 presents one sort of natural deduction system in a pretty unnatural and distinctly unfriendly way: pretty hopeless as a first introduction, say I. §2 is an over-dense treatment of soundness and completeness (a student could easily go away with the false impression that Zorn’s Lemma is needed for any completeness theorem, and so be puzzled why it doesn’t get mentioned in some versions of completeness theorems) . §3 is on Skolem functions. There are dozens of better alternatives.
So let’s move on to Chapter 4 (11 pp.) on ‘Sets again’. §1 dumps the axioms of ZFC on the reader in a take-it or leave-it spirit. §2 tells us at speed about ordinals and cardinals. §3 starts “The real numbers are constructed as follows”. And yes, all this is supposed to be wrapped up in just eleven pages. Really? Does it usefully work? What’s your guess?
As I said, a rather odd book.
The post Book note: Moerdijk & van Oosten, Sets, Models and Proofs appeared first on Logic Matters.
Book note: Moerdijk and van Oosten, Sets, Models and Proofs
Back (slowly, slowly) to logical matters. My plan for the rest of the year is to put together a second edition of what is consistently the most downloaded of the Big Red Logic Books (and also, surprisingly, the second-best paperback seller), namely Beginning Mathematical Logic: A Study Guide. It won’t be a radical revision, though I particularly want to improve the early chapter on FOL (expanding the overview, and moving the ensuing multi-recommendations into a separate chapter), and I need to write a proper chapter on type theories which I really skimped on before.
Over the coming weeks, then, as I take a look at some recent (or not so recent books) which are candidates for being newly mentioned in the Guide, I’ll post some book notes here, mostly as aides-memoire for myself. And hearing at my back time’s wingèd chariot hurrying near, I’ll probably be brisker and perhaps less patient than in the past. Make of such notes what you will.
 I did, for example, quickly become impatient with this really rather odd book. Ieke Moerdijk and Jaap van Oosten’s Sets, Models and Proofs (Springer, 2018) is just 113 pages long, before we get to the Appendix on ‘Topic for Further Study’. You might well predict that, in such a short compass, none of the announced three big topics can possibly be dealt with both accessibly and in enough detail to make a particularly useful text. You’d be right.
I did, for example, quickly become impatient with this really rather odd book. Ieke Moerdijk and Jaap van Oosten’s Sets, Models and Proofs (Springer, 2018) is just 113 pages long, before we get to the Appendix on ‘Topic for Further Study’. You might well predict that, in such a short compass, none of the announced three big topics can possibly be dealt with both accessibly and in enough detail to make a particularly useful text. You’d be right.
Chapter 1 (36 pp.) is titled, simply, ‘Sets’. The aim is “to develop your understanding of sets beyond the use you have made of them in your first years of mathematics.” So we get, in short order, §1 on cardinal numbers and Schröder–Cantor–Bernstein, §2 on the Axiom of Choice, §3 on posets and Zorn’s Lemma and cardinal comparability, §4 on well-ordered sets and transfinite recursion, and §5 on equivalents to Choice. OK, that’s a perfectly sensible menu of topics to offer those who already have a secure grip on e.g. most of the introductory chapter on sets in Munkres’s topology book or the equivalent. But to my mind, the exposition just isn’t that reader-friendly compared with alternatives elsewhere, such as Enderton’s book. Certainly not a top recommendation.
And there is another point. Here’s the offered definition of AC:
[image error]
You’ll recognize that as the preferred categorial characterisation of choice. And no surprise there: Moerdijk and van Oosten are category theorists. And more generally, their story unfolds not as a about sets but as about sets and the morphisms between them: so functions are served up as sui generis items (and likewise, cardinal numbers in this chapter seem to be treated as sui generic objects, not explicitly identified as themselves sets). Now, in one way I’m all for this. It arguably does go with our “understanding of sets” as actually used in elementary, non-set-theoretical, mathematics (cf. Leinster’s well-known piece on rethinking set theory). However I don’t think it is best policy to proceed this way quite unannounced, in a way which could potentially puzzle the more reflective student who has been told (rightly or wrongly) that functions are sets, or who has met more conventional definitions of AC and wonders why the given one here is chosen.
Chapter 2 (43 pp.) is on ‘Models’. §1 is a preliminary section on the language of ring theory. Then §2 introduces first-order languages, and §3 is on structures for first-order languages and notions of validity and equivalence. §4 gives examples of languages and structures (for graphs, rings, vector spaces, etc.). The authors prefer the approach to semantics of a language L which adds to L a fixed constant for every object in the domain (rather than going via assignments of values to variables, or adding new temporary names for objects as needed); but there’s no discussion of why we need some such approach. Again I can only report that by my lights this basic stuff isn’t done in an especially user-friendly way; I wouldn’t recommend these compressed sections as a starting-point for self-study.
§5 is on compactness. And this is actually quite nicely done. You could give this to a student who has previously met the compactness theorem as an easy corollary of the completeness theorem, (a) to provide revision on some of the elementary implications of compactness, and then (b) to display a purely semantic proof of compactness using ultrafilters.
Following on §6 is on substructures and elementary substructures, §7 is on quantifier elimination, §8 is on the Löwenheim-Skolem theorems, and 9 deals with categorical theories. All good topics — but in just 17 pages? These sections could provide useful revision material, I guess, but are again surely not the place to start. Still, Chapter 2 §§5–8 is the best bit of the book.
Chapter 3 (22 pp.) discusses ‘Proofs’. §1 presents one sort of natural deduction system in a pretty unnatural and distinctly unfriendly way: pretty hopeless as a first introduction, say I. §2 is an over-dense treatment of soundness and completeness (a student could easily go away with the false impression that Zorn’s Lemma is needed for any completeness theorem, and so be puzzled why it doesn’t get mentioned in some versions of completeness theorems) . §3 is on Skolem functions. There are dozens of better alternatives.
So let’s move on to Chapter 4 (11 pp.) on ‘Sets again’. §1 dumps the axioms of ZFC on the reader in a take-it or leave-it spirit. §2 tells us at speed about ordinals and cardinals. §3 starts “The real numbers are constructed as follows”. And yes, all this is supposed to be wrapped up in just eleven pages. Really? Does it usefully work? What’s your guess?
As I said, a rather odd book.
The post Book note: Moerdijk and van Oosten, Sets, Models and Proofs appeared first on Logic Matters.
Let’s remember how benign the internet can be
In 2002, when the internet was still in its infancy, the philosopher Bernard Williams wrote:
Moreover, the Internet shows signs of creating for the first time what Marshall McLuhan prophesied as a consequence of television, a global village, something that has the disadvantages both of globalization and of a village. Certainly it does offer some reliable sources of information for those who want it and know what they are looking for, but equally it supports that mainstay of all villages, gossip. It constructs proliferating meeting places for the free and unstructured exchange of messages which bear a variety of claims, fancies, and suspicions, entertaining, superstitious, scandalous, or malign. The chances that many of these messages will be true are low, and the probability that the system itself will help anyone pick out the true ones is even lower. In this respect, post-modern technology may have returned dialectically to a transmuted version of the pre-modern world, and the chances of acquiring true beliefs by these means, except for those who already have knowledge to guide them, will be much like those in the Middle Ages. At the same time, the global nature of these conversations makes the situation worse than in a village, where at least you might encounter and perhaps be forced to listen to some people who had different opinions and obsessions. As critics concerned for the future of democratic discussion have pointed out, the Internet makes it easy for large numbers of previously isolated extremists to find each other and talk only among themselves.
Prescient words — indeed much-quoted on the internet of late — whose bleak thought is only too well confirmed by various recent and ongoing events.
So sometimes we do need to remind ourselves about just how many small corners of the internet are thoroughly benign and life-affirming, delightful sources of innocent entertainment or diverting information, helping us to enjoy the off-line, real world, all the better.
Here’s a lovely example. When Ben Colburn, now a philosophy professor in Glasgow, was a student here twenty years ago (twenty years? ye gods and little fishes!), he started a website in which he recorded his explorations of the old parish churches in and around Cambridge, eventually ranging over all Cambridgeshire and sometimes a bit beyond (with photographs by his partner Mark Ynys-Mon). I’ve just seen that, now at last, all 206 churches are finally listed, the labour of love finishing appropriately enough with Great St Mary’s in Cambridge: “I decided that there would be something narratively satisfying about the very final church I wrote about being the church which sits at the centre of Cambridgeshire, and at the start of our journey.” Ben is a terrific guide, and revisiting the site certainly has me eagerly planning days out for when I can drive again. So warm thanks to him!
The post Let’s remember how benign the internet can be appeared first on Logic Matters.
August 8, 2024
Marshalling the grey cells …
You now know why I wrapped up work on Introducing Category Theory a bit prematurely, and paperbacked what I frankly admitted was/is a beta version, broadly functional but surely not bug-free. I got an earlier-than-expected slot for my scheduled heart operation, and just didn’t know when (or indeed if) I would be up for returning to improve the book as I would like. I suspected, rightly, that — at the least — concentration and energy would be in pretty short supply for a while!
Let me toot my own trumpet (go on, cut the convalescent some slack here!). There are, I’ve just today discovered, some cheeringly nice remarks about the book (or at least about earlier draft PDF versions) out there in some discussion forums. For example “I think Peter Smith’s book on category theory … is probably the best introduction there is. It’s very carefully written (Smith is a logician), and Smith is very good at explaining what is actually going on.” “My favourite introduction to category theory is Peter Smith’s notes. They are very gentle, and Smith does a good job of highlighting conceptual and foundational issues without it detracting from the mathematics.” “By far the best place to start, I think, is Peter Smith’s category theory notes.” “If you do struggle with the category theory, I really recommend Peter Smith’s notes. Smith is a logician and philosopher, and he is really good at explicating the conceptual aspects of category theory, not just the technical parts.” And there’s also a recent Amazon review of the book version of Part I: “The ideal starting point for category theory. Perfect for beginners. If you’re more seasoned, just read faster and supplement with “industrial-grade” readings.”
Those comments are really good to see. I make no claim for the notes other than that they are written up a bit more in the style of an elementary logic text than is usual. Of course, they will be too slow-moving, too pedestrian, for many. But it seems that some others, as I hoped, will appreciate the gentle approach.
I’d thought that post-operation recovery days would give a lot of time for catching up on reading some recently published novels. Not so! Levels of concentration have indeed not been great. But also — a more interesting phenomenon — I’ve found that, now it comes to it, I’ve wanted instead to re-visit old favourites. So, just as in hospital I found myself watching the TV news and some other factual programmes more often that usual, as if wanting to re-anchor myself to the real world as the after-effects of anaesthesia and morphine wore off, so I find myself wanting to be back for a few chapters in Barchester, or in Highbury, or on Levin’s estate, or in Wodehouse-land, just because those worlds are so comfortingly long familiar. Memo to self, though: it really is time I re-read all of Anna Karenina once more.
I got a 15″ M2 MacBook Air a bit over a year ago, and it is terrific — perfect in its intended role as a stay-at-home but move-from-room-to-room, laptop/table-top. The additional screen real-estate over the 13″ is very definitely worth having e.g. for LaTeX. In fact, I’ve found myself using my iMac less and less. And then, when I have used the iMac for multi-window work — e.g. most recently, when indexing Introducing Category Theory — I’ve found the iMac a bit frustrating, wishing the screen were that bit bigger again. So, I promised myself a somewhat indulgent treat if I got through the operation ok, namely to trade in the iMac for an Apple Studio Display. Which has arrived. And as you can see, looks just fantastic. I played a bit this afternoon with e.g. LaTeX windows open and a PDF of another book on screen, and it works brilliantly.
Oviously, then, my productivity is going to zoom up. Ahem.
OK, ok: but it is — at any rate — a lovely bit of kit which will be a delight to work with.
To work with, that is to say, when I can marshal again enough grey cells to march in step at the same time! I’m getting there, but as David Auerbach put it, recovery from major surgery is typically neither linear nor monotonic. But the trend line is encouraging enough. So onwards. Meanwhile, let me share a link that David sent me: Bach’s great Chaconne as you have never heard it before:
The post Marshalling the grey cells … appeared first on Logic Matters.
July 30, 2024
Back, and in reasonable working order …
With huge thanks to the terrific (and uniformly kind) medical staff at the much admired Royal Papworth Hospital, here I am back home, after needed but non-urgent open-heart surgery, complete with a patched ascending aorta and a new heart valve. Some residual aching and annoying post-operative insomnia, but I was already able to walk normally half-a-mile each way to sit by the river, nine days after surgery. Which surely counts, in fact, as more than reasonable. So fingers crossed for a continuing rapid recovery. (But I don’t expect there will be logical posts here for a week or two!)
The NHS might have its real problems, especially in poorer regions of the UK: but for me here in Cambridge it has worked quite brilliantly. I am duly deeply grateful.
The post Back, and in reasonable working order … appeared first on Logic Matters.




