Peter Smith's Blog, page 6
January 25, 2025
Pavel Haas Quartet and Boris Giltburg
The Pavel Haas Quartet were in Cambridge last night, playing selections from Dvořák’s ‘Cypresses’, Martinů’s fifth string quartet, and then (with Boris Giltburg) Brahms’s third piano quartet. The Martinů in particular was just stupendous. (They have programmed other Martinů quartets in recent and future concerts: and on BBC’s In Tune the other evening, we heard that the PHQ are recording four of his quartets in May. That promises to be another of their unmissable CDs.)
It was the first time I’d seen the PHQ since they settled on their new young violist, Šimon Truszka. He seemed to me not only an impressive player but also a quite wonderful fit, matching — when called for — the richness and attack of Peter Jarůšek’s cello. Let’s hope that the four of them now continue happily together after those unwanted years of change and change again after their founder violist Pavel Nikl felt he had to leave because of family tragedy.
The PHQ and Boris Gilburg also played the Martinů and the Brahms a few days earlier at Wigmore Hall, that time starting the concert with Five Pieces for String Quartet by Schulhoff. You can see a terrific recording of that concert for the next four weeks, linked above.
The post Pavel Haas Quartet and Boris Giltburg appeared first on Logic Matters.
January 14, 2025
Hibernating, hallucinating, Haydn
 Ely Cathedral, by Veronica in the Fens
Ely Cathedral, by Veronica in the FensIt has been very wintry. At least by Cambridge standards. So up late, early to retire. Hardly leaving the house for a few days. Hibernating. Mrs Logic Matters has wonderful bread and other goodies to show for it. I seem to have been staring at screens to no real effect. Mists outside seeping into the brain.
Though yesterday, as the fog lifts, a galling realization. Reading what I’d written in ICT about the subobject classifier of Set→, I think it is just wrong. There is a confident assertion that the resulting internal propositional logic is the Gödel logic G3. How on earth did I hallucinate that? Very dispiriting!
In fact, I’m not sure that any familiar “naturally occurring” topos has G3 as its internal propositional logic. For the moment, at any rate, it’s a mystery how I fouled-up like that. Not exactly confidence-inspiring. Today’s task: re-gathering scattered brain cells, and repairing the damage!
I’ll need some cheering Haydn as the background playlist. How about starting with the latest in the ongoing cycle of his symphonies from Giovanni Antonini with Il Giardino Armonico and the Basel Chamber Orchestra? That should fit the bill!
The post Hibernating, hallucinating, Haydn appeared first on Logic Matters.
January 10, 2025
Small categorial update

There’s now a new version of the category theory notes online, still missing the last chapter. It is four pages longer though, because I’ve added a section on conditional arrows in a topos (to go alongside conjunction and disjunction), and so been able to improve the presentation of (relative) pseuodo-complements. It now seems to be that my previous decision to skirt round these gadgets just left things in a pretty unsatisfying state (and when I returned to the topic, the penny belatedly dropped about how to present things quite neatly). Better late than never. There are also some other improvements, including rectifying a careless failure to keep notation consistent between Parts I and III. How exciting.
The post Small categorial update appeared first on Logic Matters.
January 3, 2025
Introducing Category Theory, 2nd edn

I have just put online a draft of all but the last chapter of a second edition of Introducing Category Theory.
I hope to have this completed and paperback-ready in February or March. In the meantime, I have “unpublished” the first edition (so that there won’t be dozens of really annoyed readers who fork out for the first edition this month only to find it superseded in a couple of weeks).
As I noted before, the obvious major change is that the second two parts (on Yoneda/adjunctions etc., and on elementary toposes) now appear in a more conventional order. But there are a lot of minor improvements along the way, as well as corrections of the typos I spotted (though naive induction suggests that I will have still missed a lot — so do let me know about any needed corrections you spot, however small).
So the first task over the next couple of weeks or so is to get things straighter in my head about ETCS so I can get a satisfactory version of the final chapter. Relatedly, if you haven’t seen it, Tom Leinster now has a substantial set of notes online for a lecture course he gave last term on set theory done in a categorial spirit (without mentioning categories). An interesting project indeed: but I’m not yet clear quite what it really teaches us.
The post Introducing Category Theory, 2nd edn appeared first on Logic Matters.
December 31, 2024
Vermeer revisited

Let me share (almost!) one of my Christmas presents with you.
Of the books I have enjoyed most during this past year, three are books on art. I have already really warmly recommended here the wonderful catalogue for the still-current exhibition Van Gogh: Poets and Lovers. And then with great enjoyment and great admiration I have reread Laura Cumming’s quite beautifully written Thunderclap.
That book about the Delft painter Fabritius (and so much more) left me wanting to get to know his work and that of his more-or-less contemporaries rather better. So for Christmas, I found myself a perfect (and cheap!) second-hand copy of the weighty and beautifully produced book that accompanied a blockbuster exhibition Vermeer and the Delft School, shown at the Metropolitan Museum of Art and then at the National Gallery back in 2001. This has turned out to be simply stunning, and has given/will give hours of unalloyed pleasure.
And you can, to a good extent, share the pleasure if you want. For a PDF of the book is quite freely downloadable from the MMA website. So, enjoy! — though I suppose you will really need a large enough screen to get something like the best experience. But do give it a try.
Happy New Year.
The post Vermeer revisited appeared first on Logic Matters.
December 24, 2024
A Christmas card
 Rest on the Flight into Egypt, Fra Bartolomeo, c. 1500 (Palazzo Vescovile, Pienza)
Rest on the Flight into Egypt, Fra Bartolomeo, c. 1500 (Palazzo Vescovile, Pienza)What the Donkey Saw
No room in the inn, of course,
And not that much in the stable,
What with the shepherds, Magi, Mary,
Joseph, the heavenly host —
Not to mention the baby
Using our manger as a cot.
You couldn’t have squeezed another cherub in
For love nor money.
Still, in spite of the overcrowding,
I did my best to make them feel wanted.
I could see the baby and I
Would be going places together.
U.A. Fanthorpe
It hasn’t been the best of times chez Logic Matters. Major heart surgery for me; much anxiety having its effects on Mrs Logic Matters too. But we end the year in much better spirits.
And heavens, compared with so many in these troubled times, we are safe and comfortable and at peace. We are not having to go places, to flee war or famine or persecution. We can indeed be truly thankful and have a very good Christmas.
I hope you and yours also have a happy Christmas and a very peaceful New Year.
The post A Christmas card appeared first on Logic Matters.
December 19, 2024
A categorial end in sight

I haven’t been posting regular updates about work on the revised version of Introducing Category Theory, not because there’s been no progress, but because there has been little of wider interest to report.
But the end is at last in sight. I have just one chapter needing significant revision. So, the plan is to withdraw the current paperback at the end of the year. I’ll post a draft Version 2.0 online in early January, with the aim of carefully proof-reading over the following two or three weeks, and getting a new paperback out by the beginning of February. So, this is a ‘heads-up’ as they say: you probably don’t want to rush to buy yourself a copy of the current paperback for Christmas, only to find it superseded in a few weeks. …
Not that I have found much actually wrong with the current version, apart from minor typos. There’s been a lot of minor rephrasing, adding a few words here or there for clarity: and a few issues (e.g. matters of ‘size’) are — I hope — somewhat better explained. However, I have also latterly settled on one big change.
Currently — after looking inside categories in Part I, talking about products, equalizers, exponentials, etc. — I go on to discuss one particular kind of category, elementary toposes, in Part II; and only in Part III do we meet those core categorial ideas, functors, natural transformations, Yoneda, adjunctions. This is a sort-of logical progression as we certainly can make a first acquaintance with toposes, their internal logic, and eventually e.g. with ETCS, without having to wield the more abstract categorial apparatus. But many, I know, do find this unusual order of business a bit off-putting (even though I loudly say that you can jump over Part II if you want). So, in Version 2.0, I’ve decided with some regrets to take after all the more conventional path and I have swapped the order of the materials: subobjects and their classifiers get moved to Part I; functors etc. etc. now appear in Part II; Part III is by way of an afterword on toposes. (This swap didn’t in fact occasion a significant amount of work in itself.)
I suppose this kind of major structural change could warrant calling the result a new edition. But having rather messed up previously, stupidly putting out into the world PDF versions with different titles, and paperbacks with three different ISBNs, I won’t complicate things any more: I’ll preserve the title and current ISBN. Watch this space for more news in due course.
The post A categorial end in sight appeared first on Logic Matters.
December 15, 2024
Not in Florence

Back in the day, not so long ago, we went a number of times to Florence just before Christmas. The best time to go, with the city returned to the Florentines, with so few tourists, the shops festive, and the restaurants relaxed and pleased to see you. And the galleries and museums are almost empty — you can wander so slowly and peacefully. We have, for example, even had to have the lights especially turned on for us in the Chapel of the Magi in the Palazzo Medici Riccardi to see Gozzoli’s stunning frescos. But after some trying months, we couldn’t quite muster the required zest and get-up-and-go to travel this year. So this is written from home instead.

But there arrived today (another) book about one of my favourites among the Florentine artists — an as-new (yet remarkably cheap) copy of the very large-format volume on Ghirlandaio in that terrific old Masters of Italian Art series. And the really spacious pages for once do justice to the extraordinary frescos in Santa Trinita and Santa Maria Novella. Not quite the magic of being there in the Tornabuoni Chapel, and seeing for example the Visitation again (as pictured above) with the poignant portrait of Giovanna degli Albizzi Tornabuoni, already dead at the age of twenty in her second pregnancy, and here memorialised for ever. But it is a real delight to slowly browse through the book by a warm fire on a cold evening, not in Florence. And next year, maybe …?
The post Not in Florence appeared first on Logic Matters.
December 3, 2024
Yanofsky, Monoidal Category Theory — 3

Some brief comments on Chapters 2 to 4 of Yanofsky’s book, firstly on the main sections of those chapters. In Chapter 2, categories are defined, we meet lots of examples, and then different kinds of arrows are defined, along with subcategories and opposite categories, and a little more. Chapter 3 then treats “structures within categories”, meaning products and coproducts (at some length) and then other limits (more briskly). A quick look at slice and co-slice categories is tacked on the end. Chapter 4 then discusses “relationships between categories”; so we meet functors, natural transformations, adjunctions, Yoneda and more.
These chapters therefore aim to cover a very familiar menu — much the same, for example, as in Tom Leinster’s excellent Basic Category Theory. Yanofksy’s sections take 129 (larger) pages, while Leinster takes 162 (smaller) pages and goes a little further. Now, as I mentioned before, I do like the order in which Yanofksy approaches the material. However — as I already indicated in my first post about Monoidal Category Theory — I do overall considerably prefer Leinster’s treatment. Why? Because it strikes me as more elegant and better motivated. At some key points Leinster’s explanations of particular points are clearer. While his discussions of major themes can usefully be a bit more expansive.
For just one example of a particular point, both authors give only headline versions of a proof that a category with finite products and equalizers has all finite limits. But Yanofsky’s version (p. 109) seems pretty under-described: I doubt that a neophyte will be able to work out a detailed proof. Leinster gives the reader significantly more hints of how to proceed.
For just one example of the treatment of a major theme, you could compare Yanofsky’s six brusque pages around and about Yoneda with Leinster’s more generous and helpful dozen.
And so it goes: examples can be multiplied. Yes, Leinster’s book is “developed out of masters-level courses”, while Yanoksky says in his Preface “we do not assume the reader is already a mathematician”. But in fact, when it gets down to business, I think seriously tackling Yanoksky’s book requires a level of mathematical maturity broadly comparable to what it takes to tackle Leinster’s. So Basic Category Theory still gets my vote for its coverage of the basic menu if you want something at that level. While my Introducing Category Theory (or more specifically, Parts I and III in the currently available version) is freely available if you want a more relaxed and slower-moving treatment of the same topics with more proofs fully spelt out.
But what about the added ‘mini-courses’ which end each of Yanofksy’s chapters? Do these add value? They are a very mixed bag. Chapter 2 adds a sixteen page mini-course on ‘Basic Linear Algebra’: I suspect most readers would either need somewhat less (if just seeking quick reminders for later use) or want significantly more (if this is actually all news to them). Chapter 3 adds thirty pages on ‘Self-Referential Paradoxes’: I’ll return to this in a future post. Then Chapter 4 has a seventeen page mini-course on ‘Basic Categorical Logic’. I’ll here say just a bit more about this last section.
If you are looking for excitements, e.g. an explanation of why the internal logic of a topos is intuitionistic by default, then this isn’t for you! (We don’t meet toposes for another 300 pages). Nor, rather oddly, do we get an elucidation of the Galois connection between syntax and semantics. Rather, Yanofsky is concerned with the elementary points that we can see conjunctions (logical products) as products in the categorial sense, we can see conjunction as left adjoint to implication, and more interestingly there are adjunctions between universal and existential quantification and a certain operation which adds a free variable.
To my mind, Yanofsky makes rather heavy weather of this. And along the way he says a number of things which will annoy logicians. We are told that “the predicate 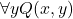 is true iff …”: predicates aren’t true or false. We are told that a dyadic predicate has a set of pairs as its “domain of discourse”: predicates don’t have domains of discourse. And so on.
is true iff …”: predicates aren’t true or false. We are told that a dyadic predicate has a set of pairs as its “domain of discourse”: predicates don’t have domains of discourse. And so on.
Our author ends with wildly over-excited claims for category theory in its applications to baby logic. Thus “We showed that the various logical operations do not stand alone. Category theory shows that the operations are intimately connected to each other and can be defined in terms of each other with universal properties.” It is logic, not category theory, which shows that some familiar logical operations are intimately connected to each other and can be defined in terms of each other: giving a categorial spin adds very little. Again “We showed that many of the truths of propositional and predicate logic are simple consequences of the universal properties of the operations. A logical statement is not true because it seems true [wow, that’s news?!]. Rather, the statement has to be true because of the way that operations are defined in terms of other operations.” But again, that’s just logic for you — nothing to do with category theory.
The post Yanofsky, Monoidal Category Theory — 3 appeared first on Logic Matters.
November 24, 2024
Arnie Koslow, 1933–2024

I was really saddened to learn yesterday of the death last month of Arnie Koslow at the age of 91.
I got to know Arnie well when I returned to Cambridge where he was a regular summer visitor for quite a few years. He became a warm friend and we spent many hours talking philosophy, and many more gossiping about a hundred things, over a glass or two, often with Hugh Mellor. Arnie really was a polymath who knew a great deal about a great deal, but was also the nicest of men. I have such fond memories.
There is an , and I do hope there will be more reminiscences at the Leiter blog.
The post Arnie Koslow, 1933–2024 appeared first on Logic Matters.



