Peter Smith's Blog, page 9
September 9, 2024
Book note: Machover, Set theory, logic and their limitations
As I said, I’d like to put together a second edition of Beginning Mathematical Logic: A Study Guide. So to that end I’m planning to revisit some of the more introductory books that should (or maybe should not) get more attention in the Guide. I’ve stacked a pile of a dozen texts on my desk to browse through, which will keep me busy enough when in the mood over the next couple of months or more. I’ll occasionally add some more book notes here as I go along, mostly as aides memoires for myself, but some might find them of interest.
There are some dauntingly large (though potentially inviting) books in the pile. But after tackling Marker’s new heavy-duty text, I’m giving myself a much easier ride next, revisiting a relatively short and well-regarded introductory text from almost thirty years ago, which rather oddly isn’t even fleetingly mentioned in the current Guide …

Back in the day, Moshé Machover together with his colleague John Bell wrote a very substantial graduate-level text A Course in Mathematical Logic (North-Holland 1977). I’ll say something more about this in another post, though — spoiler alert! — I’m not sure there are now too many reasons to revisit this book almost fifty years on.
Machover’s later, and much shorter, Set Theory, Logic and their Limitations (CUP , 1996) gives us a significantly more reader-friendly introduction to some of the topics of the big book. It is based on his notes for courses given to undergraduate philosophers and mathematicians in the University of London. The style of presentation of the technical material is mathematical: but, as Machover says, “philosophical and methodological issues are often highlighted instead of being glossed over, as is quite common in texts addressed primarily to students of mathematics.” So this promises to offer an introductory text very much in the style that the Guide favours.
How does the story in the book unfold? Ch. 1 is a quick introduction (for those that need one) to arguments by mathematical induction. And yes, in the next edition of the Guide, I should probably better highlight the need for the less mathematical beginner to get familiar with such arguments — e.g. from Velleman’s How to Prove It, or indeed from Machover’s accessible short chapter here.
Chs 2 to 6 (92 pp.) then provide an introduction to semi-formal set theory, getting as far as equivalents of the Axiom of Choice and the arithmetic of the Alephs (it’s semi-formal in that we go beyond informal naive set theory, and are introduced to the ZFC axioms, but on the other hand we don’t yet have an official formal deductive system). This is all very clearly done, I think. But arguably, for many readers Machover’s treatment will fall between two stools. On the one hand, it goes further than explaining the basics of naive informal set theory taken for granted in many logic texts; on the other hand, if you are going to tackle as much material, the somewhat more expansive coverage in e.g. Enderton’s introductory book will probably engender more understanding.
Next, Chs 7 and 8 (93 pp.) are on propositional and first-order logic. Now, the proof systems here for PL and FOL are pretty conventional Hilbert-style. And the syntax and semantics for FOL is also conventional, so the same letters can occur as parameters and as parts of a quantifying operator, with the consequent need to fuss about free vs bound occurrences of variables, and fuss too about substitution, variable capture etc. (Interestingly, in the Introduction to their big book, Bell and Machover do note that these rebarbative complexities — their phrase! — could have been avoided by using different symbols for free and bound variables, and they offer what strike me as somewhat feeble reasons for sticking to the Tarskian line.)
There is quite a bit of careful commentary and explanation as we go through these chapters. But my sense is that as get on to the proof of completeness for FOL, for example, the presentation becomes a notch or two less beginner-friendly than some of the alternatives. But that‘s quite a close call: these chapters should probably get a friendly mention in the Guide when I return to compare them directly to the current recommendations.
Finally, Chs 9 and 10 (81 pp.) first give a quite informal introduction to the ideas of computable functions and computable enumerability (informal in the sense that we don’t get official accounts of Turing machines, register machines, partial recursive functions and the like). But it is shown — indeed as in the opening chapters of my IGT — that you can already establish a range of significant results. Then we meet the MRDP theorem, which isn’t proved though its content is clearly explained.
The final chapter then turns to formal theories of arithmetic (both a series of computably axiomatised theories and True Arithmetic). With the MRDP theorem taken for granted, it is shown e.g. that True Arithmetic is not computably axiomatizable, and ultimately we reach rather strong semantic and syntactic versions of the first incompleteness theorem. So Machover’s path through this material is not a usual one, and his discussion in the last two chapters is all the more illuminating for that. Definitely to be recommended, then, as supplementary reading on these topics.
I can’t explain why Set Theory, Logic and their Limitations, though sitting on my bookshelves, dropped below my radar when writing versions of what became the Guide. A strange omission, it now strikes me.
The post Book note: Machover, Set theory, logic and their limitations appeared first on Logic Matters.
September 7, 2024
Book note: Marker, An Invitation to Math. Logic, IV
 Part IV of Marker’s book, ‘Arithmetic and Incompleteness’ is the longest, at over 100 pages, but I’ll be briefer.
Part IV of Marker’s book, ‘Arithmetic and Incompleteness’ is the longest, at over 100 pages, but I’ll be briefer.
The first chapter, Ch. 13 on the incompleteness theorems, is reasonably accessible, though for various reasons it wouldn’t be my recommendation for a place to start on the topic; still, this could provide useful follow-up reading for beginners.
Ch. 14 is on Hilbert’s 10th problem. We don’t get quite a full proof of the MRDP theorem, with all the dots joined up; but this is pretty clearly done, I think, and so without too many tears you’ll get a decent sense of what is going on. However, the nice book in the AMS Student Mathematical Library by Murty and Fodden is still clearer, more inviting, and indeed more complete: I’d read the appropriate sections of that instead.
Ch. 15 is titled ‘Peano Arithmetic and  ’. This long chapter aims at a proof of the Kirby-Paris theorem that Goodstein’s Theorem is unprovable in PA. As Marker himself clearly acknowledges with thanks, the line of argument follows closely an unpublished piece by Henry Towsner. I think you’ll want to read Marker’s chapter and Towsner’s piece in tandem — Marker is clearer, e.g., about the Hardy hierarchy of fast-growing functions, Towsner is perhaps clearer about what’s going on with the Schütte-style infinitary deduction system for arithmetic on which the overall proof turns. This two-pronged approach should then work well, and I think this is the chapter of Marker’s book that I found the most helpful addition to the literature.
’. This long chapter aims at a proof of the Kirby-Paris theorem that Goodstein’s Theorem is unprovable in PA. As Marker himself clearly acknowledges with thanks, the line of argument follows closely an unpublished piece by Henry Towsner. I think you’ll want to read Marker’s chapter and Towsner’s piece in tandem — Marker is clearer, e.g., about the Hardy hierarchy of fast-growing functions, Towsner is perhaps clearer about what’s going on with the Schütte-style infinitary deduction system for arithmetic on which the overall proof turns. This two-pronged approach should then work well, and I think this is the chapter of Marker’s book that I found the most helpful addition to the literature.
The shorter final Ch. 16 is titled ‘Models of Arithmetic and Independence Results’. After a section on provably total functions of PA, the chapter dashes on to establish the unprovability in PA of the Paris-Harrington Principle in Ramsey Theory. So there is some speedy setting-up of context, and then a dense proof. Then the discussion rushes on to a number of other results in the model theory of PA (Gaifman’s Splitting Theorem, Bounded Recursive Saturation, Tennenbaum’s Theorem). We are back, then, to topics tackled at pace. Almost anyone who wants to understand this material will be much better off working through Kaye’s approachable — indeed, one might say, particularly inviting — book Models of Peano Arithmetic.
Summary verdict? Overall I’m disappointed. Marker’s book has its moments, but it too often provides a bumpy, breathlessly fast, ride — so it is not so much the promised introduction, as a book that can be mined for supplementary/more advanced reading on some of its topics.
The post Book note: Marker, An Invitation to Math. Logic, IV appeared first on Logic Matters.
‘Men, eh?!’

Belatedly down to the Fitzwilliam Museum to see Botticelli’s Venus and Mars, which has been on a temporary loan here from the National Gallery.
I thought that the way it was displayed was very disappointingly unimaginative. The painting quite probably started life set into wooden panelling in a bed chamber, and the relatively small room used in the Fitz would have lent itself to being decorated accordingly, to give the sense again of a magical window out. But we got pink/cerise walls which to my eyes dulled the colours in the painting. And the wall-captions were pathetically bad. There was almost nothing to contextualise the painting, or the then-familiar stories of Venus and Mars, and the way that Venus played the role of tempering the less admirable traits of the god of war — instead we got a banal invitation to reflect on how ideas of sex and power had changed (changed from what?).
But, having grumpily said that, it was wonderful to see the painting again in person, so to speak. And as Botticelli makes me smile as he reverses what became the usual trope of a naked Venus and one clothed male or another, these days I’m struck by that hint — just a fleeting hint — in Venus’s expression that she too is quietly amused by the whole scenario. Almost as if she is thinking “Men, eh?!”.
The post ‘Men, eh?!’ appeared first on Logic Matters.
September 4, 2024
Book note: Marker, An Invitation to Math. Logic, III
 Part III of Marker’s book gives us a 63 pp. introduction to the theory of computability. Ch. 9 explores models of computation, first very briskly introducing unlimited register machines. We next meet primitive recursive functions, and then the partial recursive functions. It is then proved that the partial recursive functions are exactly those partial functions computable by a register machine; and we get a bit more evidence for Church’s Thesis by noting that machines with random access memory won’t compute more. The chapter — under 20 pages before the Exercises start — ends with a very quick glance at Turing machines.
Part III of Marker’s book gives us a 63 pp. introduction to the theory of computability. Ch. 9 explores models of computation, first very briskly introducing unlimited register machines. We next meet primitive recursive functions, and then the partial recursive functions. It is then proved that the partial recursive functions are exactly those partial functions computable by a register machine; and we get a bit more evidence for Church’s Thesis by noting that machines with random access memory won’t compute more. The chapter — under 20 pages before the Exercises start — ends with a very quick glance at Turing machines.
So this all proceeds at a breathless pace. There are just three sides on URM machines, just two on Turing machines. The reader is left to work out the motivation for the official definition of a primitive recursive function from the examples that actually follow that definition. Again, the move from primitive recursive to partial recursive functions is done at pace (and after just a page, we immediately meet an Ackermann-style function as an example of an intuitively computable and total recursive but not primitive recursive function). None of the ideas thus far are hard, of course: but there are some quite excellent, rather less breathless and hence more illuminating, alternative treatments available.
Similar remarks apply to the next two chapters. Ch. 10 is on universal machines and undecidability. It is shown that there is a universal computable functions 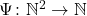 such that if
such that if 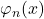 is
is 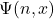 , then
, then 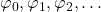 is an enumeration of all the computable (one-place) partial functions. We meet Kleene’s T-predicate, the s–m–n theorem, then the unsolvability of the halting problem leading to the undecidability of first-order validity. And next it is on to Rice’s theorem and the (second) Recursion Theorem — with all this in the space of just 11 pages! Really?
is an enumeration of all the computable (one-place) partial functions. We meet Kleene’s T-predicate, the s–m–n theorem, then the unsolvability of the halting problem leading to the undecidability of first-order validity. And next it is on to Rice’s theorem and the (second) Recursion Theorem — with all this in the space of just 11 pages! Really?
Then Ch. 11, only a couple of pages longer, discusses computably enumerable sets, many-one reducibility, computably inseparable sets, the arithmetical hierarchy, Kolmogorov randomness and more. To be frank, I see nothing to be gained by rushing through at this pace. Setting aside the very last topic, the beginner — and especially one engaged in solo self-study — will assuredly get a better conceptual understanding of what is going on by tackling, e.g., the more expansive early chapters of Cutland’s classic text instead of these three rushed chapters by Marker.
Now, Chs 9 to 11 may fly by at unhelpful speed, but the topics covered there are, we can readily agree, entry-level. By contrast, Ch. 12 on Turing Reducibility rachets up the level of sophistication significantly — it is still only 14 pages, yet we get as far as Friedburg-Muchnik (which e.g. Cutland says is beyond the scope of his book, but which is proved by Cooper in his more advanced text but not starting until his p. 238) and the Low Basis Theorem (Cooper p. 330). Assuming you come primed with a strong enough understanding of basic computability theory, you could perhaps usefully tackle this chapter (these upper-level topics are of course intrinsically interesting). But again my sense is that the slower presentation of Friedburg-Muchnik in Cooper (say) is much more likely to engender a deeper understanding of the priority method used in the proof.
So, a summary verdict on Part III: too much is done too quickly for a first encounter with this material. Of course, this could be useful revision/consolidation material for enthusiasts who like Marker’s brusque style; though, by my lights, there are more attractive alternatives for that too.
The post Book note: Marker, An Invitation to Math. Logic, III appeared first on Logic Matters.
September 1, 2024
Schubert on Sunday 10: Trio Bohémo play Schubert
Of the making of quite outstanding Czech (or perhaps we should say, Czech and Slovak) chamber music ensembles, there is no end. Now the young prize-winning Trio Bohémo have just released their first CD — and they have been nothing if not ambitious, tackling Smetana’s only piano trio and the second of Schubert’s trios. Katherine Cooper in her very warm review for Presto Music writes: “At full tilt, these musicians generate the same sort of gutsy firepower that we’ve come to expect from their compatriots in the Pavel Haas Quartet, but the fine-boned quality of their pianissimo playing is equally impressive (and beautifully captured by the sound-engineers at Snape Maltings) … All in all, it’s a supremely assured debut recording, full of sensitivity and subtlety.” That seems just right. So here’s a live recording of the Trio Bohémo playing the Schubert about three years ago. Enjoy!
The post Schubert on Sunday 10: Trio Bohémo play Schubert appeared first on Logic Matters.
August 30, 2024
Six weeks, and counting …

The flurry of book notes will calm down for a while. For it is six weeks today since my open-heart surgery, and that means I can (at last) drive again. Another significant waymark on the route back to normality.
Off we went, then, this morning to Anglesey Abbey a few miles out of Cambridge, the nearest National Trust property. So familiar but a real delight to walk through part of the gardens for a couple of miles or so in breezy late summer sun. And the ideal weather promises mostly to hold for the next week. I rather think that more strictly logical matters can wait for a bit while we range afield, out and about again!
The post Six weeks, and counting … appeared first on Logic Matters.
August 28, 2024
Book note: Marker, An Invitation to Math. Logic, I & II
 David Marker, the author of what has become a modern classic on model theory, has recently published An Invitation to Mathematical Logic (Springer, 2024). “My goal was to write a text for a one-semester graduate-level introduction to mathematical logic, one that I would have liked to learn from when I was a student, and one I would like to teach from as a professor.” Part I of the book, ‘Truth and Proof’ is on first-order logic and theories and the structures for interpreting them. Part II is on ‘Elements on Model Theory’. I’ll say something about these first two Parts here, and I’ll discuss Part III ‘Computability’ and Part IV ‘Arithmetic and Incompleteness’ in a follow-up post. (The book doesn’t discuss set theory.)
David Marker, the author of what has become a modern classic on model theory, has recently published An Invitation to Mathematical Logic (Springer, 2024). “My goal was to write a text for a one-semester graduate-level introduction to mathematical logic, one that I would have liked to learn from when I was a student, and one I would like to teach from as a professor.” Part I of the book, ‘Truth and Proof’ is on first-order logic and theories and the structures for interpreting them. Part II is on ‘Elements on Model Theory’. I’ll say something about these first two Parts here, and I’ll discuss Part III ‘Computability’ and Part IV ‘Arithmetic and Incompleteness’ in a follow-up post. (The book doesn’t discuss set theory.)
Compare these two presentations of a familiar result. Here’s Exhibit A:


And here is Exhibit B:

Which do you prefer? I vote for Exhibit A. The couple of sentences of the preamble, “The key idea is …”, are just what is needed to fix our understanding of the Tarski–Vaught claim. And then the balance of the ensuing proof is that bit nicer. The trivial cases for the induction are relegated to exercises, and the structure of the remaining case slightly better signalled (“Conversely”). [Imagine the bookwork part of an exam done under time pressure: you’d prefer something along the lines of Exhibit A, wouldn’t you, as showing the student had seen what was important?]
Now, Exhibit A is from Kirby’s excellent An Invitation to Model Theory. Exhibit B is from Marker’s new Invitation. Of course I don’t want to make anything hang on this one example. But I do think the difference between Marker and (in this case) Kirby covering this same material is in fact rather typical. I could have chosen other examples and other contrasting authors (I’ve just picked a nice short illustration). And we’d similarly see that, on the one hand, Marker tends to short-change the reader when it comes to those useful orientating sentences or two which can be so helpful (the classroom asides, the “look at it this way” guides). And on the other hand, some of his proofs can be a little ploddingly flat-footed, leaving the reader to distinguish the interesting moves from the bits where we are just joining-up-the-dots. The cumulative effect is to make Parts I and II of Marker’s book that bit less reader-friendly (especially for self-study) than he intends.
In just a little more detail, Part I (64 pp.) has four chapters. Ch. 1, ‘Languages, Structures, and Theories’ provides a terse introduction, rather short on motivations and explanations (a quite trivial but characteristic example: we are flatly told that 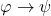 is an abbreviation of
is an abbreviation of 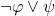 , take it or leave it, end of story: so much for calming the common student discomfort — graduate student or otherwise — with the conventional treatment of the conditional!). We get the same briskness in Ch. 2, ‘Embeddings and Substructures’ (where we find Exhibit B). The short Ch. 3 introduces one proof system for FOL, a sequent calculus, in which proofs are simple linear arrays, Hilbert-style. A perfectly serviceable system, but there’s no hint at all about different ways of doing things. Then Ch. 4 proves completeness, in places a bit laboriously. Marker does bring out nicely why the story goes a bit differently for countable languages and uncountable languages (needing Zorn’s Lemma or an equivalent in the second case). But on the other hand — the student reader might reasonably ask — given that all the examples in Ch. involves small finite languages, exactly why might we care about the uncountable case? I don’t think we are told.
, take it or leave it, end of story: so much for calming the common student discomfort — graduate student or otherwise — with the conventional treatment of the conditional!). We get the same briskness in Ch. 2, ‘Embeddings and Substructures’ (where we find Exhibit B). The short Ch. 3 introduces one proof system for FOL, a sequent calculus, in which proofs are simple linear arrays, Hilbert-style. A perfectly serviceable system, but there’s no hint at all about different ways of doing things. Then Ch. 4 proves completeness, in places a bit laboriously. Marker does bring out nicely why the story goes a bit differently for countable languages and uncountable languages (needing Zorn’s Lemma or an equivalent in the second case). But on the other hand — the student reader might reasonably ask — given that all the examples in Ch. involves small finite languages, exactly why might we care about the uncountable case? I don’t think we are told.
These chapters are of course all done perfectly respectably: but just how inviting are they? I, for one, didn’t find them particularly so, and I at least had the advantage of already knowing what was supposed to be going on.
Part II (71 pp.) again has four chapters. Ch. 5 is on compactness (introduced as a simple consequence of completeness), starting with some elementary applications but soon turning to examples you’ll need more mathematical background to understand. Ch. 6 is a somewhat dense introduction to ultraproducts, giving us another proof of compactness. Ch. 7 begins on the basic idea of quantifier elimination; but soon, as with Ch. 8, we are into fairly hardcore algebraic applications — fine for the graduate pure mathematicians with some serious algebra under their belt who are perhaps Marker’s core intended audience, but again not done invitingly enough (say I) to draw in other readers whose prime interests are more logical.
So far, then, I have to confess to being rather disappointed by a book I had higher expectations of. But how does the (perhaps less ambitious) second half of the book go?
The post Book note: Marker, An Invitation to Math. Logic, I & II appeared first on Logic Matters.
Book note: Marker, An Invitation to Mathematical Logic, I & II
 David Marker, the author of what has become a modern classic on model theory, has recently published An Invitation to Mathematical Logic (Springer, 2024). “My goal was to write a text for a one-semester graduate-level introduction to mathematical logic, one that I would have liked to learn from when I was a student, and one I would like to teach from as a professor.” Part I of the book, ‘Truth and Proof’ is on first-order logic and theories and the structures for interpreting them. Part II is on ‘Elements on Model Theory’. I’ll say something about these first two Parts here, and I’ll discuss Part III ‘Computability’ and Part IV ‘Arithmetic and Incompleteness’ in a follow-up post. (The book doesn’t discuss set theory.)
David Marker, the author of what has become a modern classic on model theory, has recently published An Invitation to Mathematical Logic (Springer, 2024). “My goal was to write a text for a one-semester graduate-level introduction to mathematical logic, one that I would have liked to learn from when I was a student, and one I would like to teach from as a professor.” Part I of the book, ‘Truth and Proof’ is on first-order logic and theories and the structures for interpreting them. Part II is on ‘Elements on Model Theory’. I’ll say something about these first two Parts here, and I’ll discuss Part III ‘Computability’ and Part IV ‘Arithmetic and Incompleteness’ in a follow-up post. (The book doesn’t discuss set theory.)
Compare these two presentations of a familiar result. Here’s Exhibit A:


And here is Exhibit B:

Which do you prefer? I vote for Exhibit A. The couple of sentences of the preamble, “The key idea is …”, are just what is needed to fix our understanding of the Tarski–Vaught claim. And then the balance of the ensuing proof is that bit nicer. The trivial cases for the induction are relegated to exercises, and the structure of the remaining case slightly better signalled (“Conversely”). [Imagine the bookwork part of an exam done under time pressure: you’d prefer something along the lines of Exhibit A, wouldn’t you, as showing the student had seen what was important?]
Now, Exhibit A is from Kirby’s excellent An Invitation to Model Theory. Exhibit B is from Marker’s new Invitation. Of course I don’t want to make anything hang on this one example. But I do think the difference between Marker and (in this case) Kirby covering this same material is in fact rather typical. I could have chosen other examples and other contrasting authors (I’ve just picked a nice short illustration). And we’d similarly see that, on the one hand, Marker tends to short-change the reader when it comes to those useful orientating sentences or two which can be so helpful (the classroom asides, the “look at it this way” guides). And on the other hand, some of his proofs can be a little ploddingly flat-footed, leaving the reader to distinguish the interesting moves from the bits where we are just joining-up-the-dots. The cumulative effect is to make Parts I and II of Marker’s book that bit less reader-friendly (especially for self-study) than he intends.
In just a little more detail, Part I (64 pp.) has four chapters. Ch. 1, ‘Languages, Structures, and Theories’ provides a terse introduction, rather short on motivations and explanations (a quite trivial but characteristic example: we are flatly told that 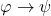 is an abbreviation of
is an abbreviation of 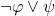 , take it or leave it, end of story: so much for calming the common student discomfort — graduate student or otherwise — with the conventional treatment of the conditional!). We get the same briskness in Ch. 2, ‘Embeddings and Substructures’ (where we find Exhibit B). The short Ch. 3 introduces one proof system for FOL, a sequent calculus, in which proofs are simple linear arrays, Hilbert-style. A perfectly serviceable system, but there’s no hint at all about different ways of doing things. Then Ch. 4 proves completeness, in places a bit laboriously. Marker does bring out nicely why the story goes a bit differently for countable languages and uncountable languages (needing Zorn’s Lemma or an equivalent in the second case). But on the other hand — the student reader might reasonably ask — given that all the examples in Ch. involves small finite languages, exactly why might we care about the uncountable case? I don’t think we are told.
, take it or leave it, end of story: so much for calming the common student discomfort — graduate student or otherwise — with the conventional treatment of the conditional!). We get the same briskness in Ch. 2, ‘Embeddings and Substructures’ (where we find Exhibit B). The short Ch. 3 introduces one proof system for FOL, a sequent calculus, in which proofs are simple linear arrays, Hilbert-style. A perfectly serviceable system, but there’s no hint at all about different ways of doing things. Then Ch. 4 proves completeness, in places a bit laboriously. Marker does bring out nicely why the story goes a bit differently for countable languages and uncountable languages (needing Zorn’s Lemma or an equivalent in the second case). But on the other hand — the student reader might reasonably ask — given that all the examples in Ch. involves small finite languages, exactly why might we care about the uncountable case? I don’t think we are told.
These chapters are of course all done perfectly respectably: but just how inviting are they? I, for one, didn’t find them particularly so, and I at least had the advantage of already knowing what was supposed to be going on.
Part II (71 pp.) again has four chapters. Ch. 5 is on compactness (introduced as a simple consequence of completeness), starting with some elementary applications but soon turning to examples you’ll need more mathematical background to understand. Ch. 6 is a somewhat dense introduction to ultraproducts, giving us another proof of compactness. Ch. 7 begins on the basic idea of quantifier elimination; but soon, as with Ch. 8, we are into fairly hardcore algebraic applications — fine for the graduate pure mathematicians with some serious algebra under their belt who are perhaps Marker’s core intended audience, but again not done invitingly enough (say I) to draw in other readers whose prime interests are more logical.
So far, then, I have to confess to being rather disappointed by a book I had higher expectations of. But how does the (perhaps less ambitious) second half of the book go?
The post Book note: Marker, An Invitation to Mathematical Logic, I & II appeared first on Logic Matters.
August 27, 2024
A quick categorial update
I have updated the downloadable PDF of Introducing Category Theory from Version 1.0 to Version 1.1, and I have also uploaded the corresponding new PDF for printing the paperback. But the latter could take a little time to percolate through Amazon’s system. The main difference is that I have simply deleted the old §5.3 (and trivially relabelled what was the final subsection of §5.2 as a new §5.3). Why the deletion? Because of an annoying/amusing/silly glitch pointed out by Matthew Bjerknes. I explain in the footnote to the corrections page for Version 1.0.
A gentle hint. If you have bought the paperback, and do like the book, it would be a kind thought to leave a (nice!) rating, if not a mini-review, on Amazon. And indeed, even if you haven’t splashed out, if you are one of those who have downloaded the PDF (over a thousand downloads so far, though who knows how many individual downloaders there are!), then — assuming you do have an active Amazon account — you can still leave a review. But then it is probably best to start along the lines of “I have read a PDF version of this book, and …”.
As noted before, the printed version of the book is priced, within a rounding error, at the very minimum that Amazon will allow, giving me a royalty of about 3p a copy (that’s pence, not pounds!). So positive ratings won’t make my fortune; however, they might help to spread the word to those suspicious of books without recommendations.
The post A quick categorial update appeared first on Logic Matters.
August 26, 2024
Book note: Roy, Symbolic Logic
There are some more warm recommendations to come. But let me rather sharply set aside another text which has been mentioned to me. I’m not consistently a harsh reader, honest — but the whole point of the Study Guide (or, as here, of preparatory readings for the next edition) is to make discriminations, more or less overtly, as best I can. The Guide would otherwise be pretty useless. So here goes …
 Tony Roy’s Symbolic Logic (self–published in 2023) is an extraordinarily long text, no less than 810 pp., which the author has made freely available as a PDF download, and also as two minimal-cost print-on-demand paperbacks from Amazon. The webpage for the book is here.
Tony Roy’s Symbolic Logic (self–published in 2023) is an extraordinarily long text, no less than 810 pp., which the author has made freely available as a PDF download, and also as two minimal-cost print-on-demand paperbacks from Amazon. The webpage for the book is here.
The book is subtitled An Accessible Introduction to Serious Mathematical Logic. But that’s perhaps rather misleading, if we read “serious” seriously. The first 500(!) pages are just entry-level first-order logic (up to and including the completeness theorem). There’s a smidgin of elementary model theory in the next 50-odd pages. Then the remainder of the book contains mostly elementary discussion of formal arithmetic, computability, recursive functions and Gödelian incompleteness.
But let’s not worry about the subtitle. I’m all for accessible introductions; and I’m certainly all for this publication model (the freely downloadable PDF, with an inexpensive paperback — or in this case two — for those who prefer to read hard-copy). So, the question is: how well does this book do its limited job?
Actually, that’s not quite the right question. I strongly suspect that the student reader who’d appreciate the very slow-moving earlier chapters (mostly the level of a first-year philosophy course, comparable to my IFL) is not the same reader who could happily tackle the later chapters (the level of a third-year course, perhaps, comparable to my IGT). But again, let’s not worry too much about that. Let’s deal the material a rough blow, and then cheerfully say that it falls naturally into two parts — the “baby logic” part (introducing propositional logic and FOL up to the completeness theorems); then elementary mathematical logic (completeness, a touch of model theory, a touch of formal arithmetic etc.). Then there are a pair of questions, one for each part. How well do they separately work?
The first part of course enters a very crowded field. I can’t say it shines. There are considerable longeurs. I can be wordy (some complain!): but Roy is much more so. And the balance of discussions can be unhelpful, for example over-emphasising the business of discovering Fitch-style natural deduction proofs (after a certain point, really who cares? it’s just not — or shouldn’t be — the point). Then there’s an idiosyncratic Chapter 7, which seems to be in wandering in the same neck of the woods as is inhabited by proofs using semantic tableaux, but is to my mind quite unclear. I’m not moved to go into more details (you can inspect the text for yourself). But this material is assuredly presented better elsewhere (in one register, for less mathematical beginners as in my IFL, in another register for the those happier with a more mathematical idiom as in e.g. the early chapters of Dag Westerståhl’s Foundations of Logic).
Likewise for the second part. The reader will have certainly have more fun and get more enlightenment from the alternatives on Gödelian incompleteness and related matters recommended in the Study Guide (now adding in the last two parts of Westerståhl’s excellent text).
A symptomatic episode: Roy hacks through forty pages establishing the second and third derivability condition for PA. Really? What mathematical illumination does this bring over and above IGT’s arm-waving three pages? Or, if you insist, over Rautenberg’s seven pages? None at all, say I. Indeed, Roy’s presentational style overall won’t, I fear, do much to engender the key thing, the mathematical/logical maturity that enables the student to tell the difference between tedious joining-up-the-dots and the significant proof-ideas.
Which is a great pity given all the effort which has gone into Roy’s book; but this is not one for the Study Guide.
The post Book note: Roy, Symbolic Logic appeared first on Logic Matters.



