Peter Smith's Blog, page 7
November 21, 2024
Yanofsky, Monoidal Category Theory — 2

I’ll offer some more comments over the next blog post or two on Chapters 1 to 4 of Monoidal Category Theory, the chapters which comprise Yanofsky’s introductory course on core category theory, before we reach the monoidal delights.
Chapter 1, after some short and very introductory sections, is mostly taken up with a 25 page mini-course ‘Sets and Categorical Thinking’. In fact, we not only meet sets and functions, but also graphs and groups and their respective homomorphisms: we get some familiar definitions, and a few results results along the way (such as that a function 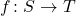 is injective iff there is a function
is injective iff there is a function 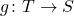 such that
such that 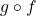 equals the identity function on
equals the identity function on  ).
).
We could quibble at various points. For example, having been told that a function  is “an assignment of an element of
is “an assignment of an element of 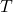 to every element of
to every element of  ”, we are then asked to buy the claim that for any set
”, we are then asked to buy the claim that for any set 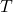 there is a function to it from the empty set. The naive reader might reasonably suppose that if
there is a function to it from the empty set. The naive reader might reasonably suppose that if  has no elements, then there is no assignment of corresponding elements of
has no elements, then there is no assignment of corresponding elements of 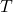 to be had. But fussing about this sort of thing would be boring, so let me cut to the chase, to make the main point about Yanofsky’s introductory remarks about sets.
to be had. But fussing about this sort of thing would be boring, so let me cut to the chase, to make the main point about Yanofsky’s introductory remarks about sets.
For Yanofksy, a set is a “collection of elements”. And he seems to place no restriction at all on the sorts of things that can be elements of sets. So we have sets whose members are numbers (p. 8), shirts (p. 8), people (p. 11), US states (p. 22), street corners (p. 24), web pages (p. 25), Facebook accounts (p. 25), ideas (p. 115) — as well as more sets. So be it. Yes, there is a debate to be had about whether talking of sets of shirts or people or ideas is more than a convenient façon de parler, a way of talking in the singular about perhaps many things at once, which could be cashed out in an alternative plural idiom without any commitment to new entities over and above the shirts, people or ideas. But that’s not a debate for here. Without getting into ontological wrangles, let’s go along with this sweepingly promiscuous use of ‘set’ (arguably indeed the everyday one) where — whatever your favourite widgets might be — there can be sets of that sort of thing.
So to the obvious question: is this understanding of ‘set’ still in play at the beginning of Chapter 2 where categories are defined, and the first example given is — as so often — “the category 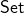 ” of sets and functions [note the definite article]? So, among the objects of the the category
” of sets and functions [note the definite article]? So, among the objects of the the category 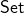 , do we find e.g. the set of Yanofsky’s shirts, and — a brand new arrival, with its newly-baked members — today’s set of Mrs Logic Matters’s excellent scones? We are told on p. 37 that “the collection of all sets form a category”, presumably the category
, do we find e.g. the set of Yanofsky’s shirts, and — a brand new arrival, with its newly-baked members — today’s set of Mrs Logic Matters’s excellent scones? We are told on p. 37 that “the collection of all sets form a category”, presumably the category 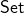 (NB the ‘all’).
(NB the ‘all’).
But I doubt that this is what Yanofsky really intends. As usually construed, “the category 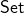 ” refers not to some fluctuating universe including sets with concrete members which may pop in and out of existence. Rather the objects of
” refers not to some fluctuating universe including sets with concrete members which may pop in and out of existence. Rather the objects of 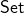 are standardly taken to be members of some hierarchy of pure sets (so its sets all the way down) as described by ZFC or some nice extension thereof. Thus, of course, Mac Lane in defining categories as implementations of the axioms of category theory in a universe of pure sets as described by ZFC plus (Categories for the Working Mathematician, pp. 10, 23). Compare Horst Schubert in his terse but very good and clear Categories (§3.1), who writes “One has to be aware that the set theory used here has no “primitive (ur-) elements”; elements of sets, or classes …, are always themselves sets.” Compare too, for example, Borceux in his Handbook of Categorical Algebra I, in his opening pages, or Emily Riehl in her Category Theory in Context, p. 6: “common practice among category theorists is to work in an extension of the usual Zermelo–Fraenkel axioms of set theory, with new axioms allowing one to distinguish between “small” and “large” sets, or between sets and classes” (but to repeat, the ZF axioms describe a universe of pure sets, where Yanofsky’s shirts and Mrs Logic Matters’s scones are not to be found!).
are standardly taken to be members of some hierarchy of pure sets (so its sets all the way down) as described by ZFC or some nice extension thereof. Thus, of course, Mac Lane in defining categories as implementations of the axioms of category theory in a universe of pure sets as described by ZFC plus (Categories for the Working Mathematician, pp. 10, 23). Compare Horst Schubert in his terse but very good and clear Categories (§3.1), who writes “One has to be aware that the set theory used here has no “primitive (ur-) elements”; elements of sets, or classes …, are always themselves sets.” Compare too, for example, Borceux in his Handbook of Categorical Algebra I, in his opening pages, or Emily Riehl in her Category Theory in Context, p. 6: “common practice among category theorists is to work in an extension of the usual Zermelo–Fraenkel axioms of set theory, with new axioms allowing one to distinguish between “small” and “large” sets, or between sets and classes” (but to repeat, the ZF axioms describe a universe of pure sets, where Yanofsky’s shirts and Mrs Logic Matters’s scones are not to be found!).
So if Yanofsky’s category 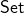 really is intended to be some fluctuating universe of sets including sets with concrete ur-elements, then our author should certainly have told us that he is taking a pretty deviant line on what
really is intended to be some fluctuating universe of sets including sets with concrete ur-elements, then our author should certainly have told us that he is taking a pretty deviant line on what 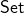 comprises as compared with standard texts. But I suspect that there is actually an unacknowledged crashing of the gears between what is being said about sets in Yanofsky’s Chapter 1 and what is being assumed in Chapter 2 onwards once the category
comprises as compared with standard texts. But I suspect that there is actually an unacknowledged crashing of the gears between what is being said about sets in Yanofsky’s Chapter 1 and what is being assumed in Chapter 2 onwards once the category 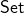 officially enters stage left, where the discussion seems to proceed in a conventional way. In which case, Yanofsky’s should have explained carefully the reasons for the radical narrowing of focus which means that
officially enters stage left, where the discussion seems to proceed in a conventional way. In which case, Yanofsky’s should have explained carefully the reasons for the radical narrowing of focus which means that 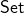 doesn’t after all contain many of the sets he has previously been talking about. (Apologies if I have missed the relevant discussion — one of the downsides of working from a physical book is I that can’t double-check with some appropriate text-searches.)
doesn’t after all contain many of the sets he has previously been talking about. (Apologies if I have missed the relevant discussion — one of the downsides of working from a physical book is I that can’t double-check with some appropriate text-searches.)
As to the remarks on ‘Categorical Thinking’ in that first mini-course, we get the usual kind of hand-waving remarks about morphisms being “central” in category theory (as if they weren’t all along in the algebra and topology we learnt back when I were a lad), or category theory not being about ‘things’ but about how ‘things’ relate to other ‘things’ (as if telling you about Jack relates to Jill I am not telling you something about Jack?). Sure, the hand-waving is fine in its place, but to my tastes Yanofsky does rather over-do it.
The post Yanofsky, Monoidal Category Theory — 2 appeared first on Logic Matters.
November 19, 2024
Yanofsky, Monoidal Category Theory — 1

I thought I should take a look at the just-published book by Noson Yanofsky, Monoidal Category Theory: Unifying Concepts in Mathematics, Physics, and Computing (MIT Press, 2024).
Yanofsky is on a proselytizing mission. He wants to persuade us that, as his Preface has it, once the language of category theory is understood “one is capable of easily learning an immense amount of science, mathematics, and computing” [sic], and “with the language of category theory in your toolbox, you can master totally new and diverse fields with ease”. Master totally new fields with ease? Really??
I don’t buy this sort of exaggeration for a moment (and neither should you). But let’s skip over the extravagant advertising spiel for now. This won’t be the first time category theory has been over-sold, and over-selling certainly doesn’t in itself mean that what follows can’t be interesting and illuminating. So, having raised a sceptical eyebrow or two, let’s move on …
This is a very long book, some 653 pages in total (it is also, by the way, a very expensive book, listed at $90/£85: I wonder, is a pricey dead-tree publication with no version free to download from the author’s website really the best way to spread the categorial gospel in 2024?) Still, Yanofsky’s long chapters naturally divide into three groups, so we can take the book in chunks. The first four chapters aim to give a basic introduction to category theory. The next three chapters are on monoidal categories. The last three chapters are on further, often more advanced, topics (including ‘mini-courses’ on homotopy type theory, knot theory, quantum computing, and more). Here in this first post, I’ll just make some rather general comments about that introductory first part, with more specific comments to come in later posts.
As Yanofsky points out, in many books, ideas such as functor and natural transformation are introduced very early on. He prefers to make a slower ascent to the more abstract heights. So we first have a chapter ‘Categories’ giving basic definitions, examples, and something about how we can get new categories from old, and a bit more. Then we have a chapter ‘Structures within Categories’ where we encounter products, equalizers, pullbacks, and their duals, and limits/colimits in general. And only then do we get a chapter ‘Relationships between Categories’ where we first meet functors and natural transformations, and go on to discuss adjunctions and eventually Yoneda.
Now, I really like this general order of business — which is, of course, the same one I have followed in Introducing Category Theory (and in all its earlier versions under different titles). So how do our respective accounts compare?
The immediately obvious difference is a matter of length. For example, leaving aside its final section — a mini-course on Self-Referential Paradoxes (about which more anon) — Yanfosky’s chapter ‘Structures within Categories’ is 28 pages long. The topics correspond pretty much to topics of my Chapters 9–12, 14, 15, 18–20 (in the current version of ICT), which come to some 70 pages. Likewise, Yanfosky’s chapter ‘Relationships between Categories’ — this time without its final mini-course titled ‘Basic Categorical Logic’ — is 67 pages long. And the coverage broadly corresponds to that of my Chapters 16, 28–45, which come to some 184 pages. What accounts for that major divergence? Sheer long-windedness on my part?
I hope not. One thing that I do which Yanofsky doesn’t is to write chapters on pre-categorial (though we might say quasi-categorial) ideas about e.g. products, quotients, and Galois connections, before introducing the categorial accounts of products, quotients and adjunctions. I suspect this reflects a difference in vision: Yanofsky perhaps sees more sheer novelty in categorial ideas than I do. He has quite a few text-boxes headed ‘Important Categorical Idea’ where I’d be tempted to say that the relevant idea is one we already repeatedly encounter in modern (but pre-categorial) abstract mathematics. Anyway, those framing chapters of mine aim to ease the path into categorial ways of thinking by more explicitly linking them to the already-familiar.
But setting aside those additions, then yes, it is often the case that when it gets down to technical details, I go more slowly and more discursively (with more ‘classroom chat’) than Yanofsky. For example, he has a 17 page section plus a couple more pages on adjunctions compared to my 36. Where he dives in, hitting the reader with four definitions of adjunctions at the outset, I give one definition and then the story more gently unfolds in a way that makes the other possible definitions emerge in a natural way. And where Yanofsky e.g. gives a short-hand one paragraph proof of RAPL (his Theorem 4.6.4), ICT offers seven shorter numbered paragraphs, carefully explaining the nuts and bolts of the same proof strategy in a way which I hope is very significantly easier to follow.
And so it goes. Tom Leinster has remarked that “the level of abstraction in the Yoneda Lemma means that many people find it quite bewildering”. So the challenge is to make Yoneda as unbewildering as possible. ICT has a couple of chapters, running to 18 pages with quite a bit of motivational chat. Yanofsky has a rapid-fire 6 pages, and I suspect many readers — if not bewildered — will remain puzzled, and unclear whether they have a grip on what’s going on.
Now, just with respect to this matter of pace, some will indeed prefer a snappier introduction to basic category theory than mine. Of course. But I think that, even though I prefer Yanofsky’s ordering of topics, the go-to faster-track option remains Leinster’s Basic Category Theory (which is a similar length to Chapters 1 to 4 of Yanofsky minus a ‘mini-course’ or two). Yes, Yanofsky’s book is officially aimed at those with less mathematical background: but, once it gets going, it too in fact requires a reader with a fair amount of “mathematical maturity”. So such a reader wanting a basic introduction could tackle Leinster’s lovely book, which is after all free to download (not a minor consideration!).
There is quite a bit more to be said, however, about Yanofsky’s opening chapters. So watch this space.
The post Yanofsky, Monoidal Category Theory — 1 appeared first on Logic Matters.
November 15, 2024
Regrouping

One of the more beautiful sights in Cambridge is the long avenue of London plane trees on Jesus Green, a delight at every time of year, equally in summer sun or on a grey autumn day with the leaves falling. It so raises the spirits every time we walk out into town. And we’ve really needed that: it has been a stressful month with a serious health scare at home. Which has very happily turned out to be a false alarm (with thanks to the NHS for extremely rapid investigations and scans). But it has all been, shall we say, rather distracting …
We are regrouping. And I’m at last in the mood again for logical matters. In particular, I’m back to revising Introducing Category Theory. I still (over-optimistically?) hope to get a Version 1.2 out by the end of the year — more than just an update for corrections, but with fewer radical changes than could warrant it being appropriately called a second edition. In the last few days, I’ve been wrangling with the early chapters on groups and categories of groups once more, I hope to some reasonably good effect.
More generally as I go through the book, I find I’m doing scattered amounts of rephrasing and making minor alterations for clarity. But so far, I’ve found no real horrors crying out for correction; and at this point, the only major additions I want to make are (1) some brief remarks about the idea of monoidal categories since these are flavour of the month (I’ll be interested to see Noson Yanofsky’s brand new book) and (2) an expanded/improved treatment of structural set theory/ETCS (I’ve been spurred on to want to do better on that in part by recently re-reading this extremely helpful piece on set theories and type theories by Mike Shulman). I’ll post any interesting-enough new sections here.
I confess that, while de-stressing after recent events, I treated myself to some serious Apple Therapy, in the form of the new, very mini, Mac Mini to drive my Apple Studio Display. I’m delighted and can warmly recommend. An indulgence, yes (though it seemed absurdly cheap with an education discount). But it really is impressive.
The LaTeX file for the 450 page category theory book (with a lot of commutative diagrams in TikZ which notoriously slow things down) compiles to a PDF in 23.80 seconds on my M2 MacBook Air, and 14.40 seconds on the M4 Mini. That’s a very noticeable speed bump. I’ll now have to work out how to to use the memoize package which avoids having to recompile stable diagrams every time you update the PDF which should speed things even more.
You don’t want my views about the way the world out there is going to hell in a handcart (for where does one start?). So I’ll try to keep posts here — or at least the non-logical ones! — more heartening. For today, then, here is a musical treat to pass on. A few years back, the BBC relayed a live concert by the wonderful Elisabeth Brauß in Birmingham playing Schubert’s Four Impromptus D.899. They have recently rebroadcast her extraordinarily sensitive performance, and for two or three weeks you can find it again here on BBC Sounds (starting at 1.48 in). Real balm for the troubled soul.
The post Regrouping appeared first on Logic Matters.
October 15, 2024
Categorial progress …

I paperbacked my gentle introductory notes on category theory sooner than ideally I would have wished. But with routine-but-major heart surgery scheduled unexpectedly early, I thought I should at least get a beta version of the book out while I could, not knowing what the future would hold.
In the last week or so, I’ve started returning to the book, since a number of issues with it have been nagging away at me. Indeed, I now have a list of well over a hundred notes-to-self, ranging from “Must be more consistent in the use of ‘one-one’ vs ‘one-to-one’’’, through relatively easy-to-fix queries like “Even if I don’t prove that the arrow ![[\top,\bot]](https://i.gr-assets.com/images/S/compressed.photo.goodreads.com/hostedimages/1729063087i/36062462.png) is monic in a topos, can’t I at least arm-wavingly say why it morally ought to be?”, and then on to heavier issues like “Maybe I really should say something about Tarski–Grothendieck universes?”, “Since I do explain about products of arrows
is monic in a topos, can’t I at least arm-wavingly say why it morally ought to be?”, and then on to heavier issues like “Maybe I really should say something about Tarski–Grothendieck universes?”, “Since I do explain about products of arrows 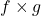 , shouldn’t I at least say something about how this leads on to the idea of monoidal categories?”. And so on.
, shouldn’t I at least say something about how this leads on to the idea of monoidal categories?”. And so on.
Working through these queries is therefore going to keep me merrily busy for some weeks as I put together a Version 1.2 of the notes. So far, delving back into elementary category theory has indeed been pretty enjoyable, not least because (and here I tempt fate) I haven’t yet found any really embarrassing mistakes in Version 1.1. Long may that last! But if you have spotted foul-ups, large or small, or have more general suggestions for improving a section, now is the time to let me know!
The post Categorial progress … appeared first on Logic Matters.
October 8, 2024
Latex pages
I’m revising/re-organizing the LaTeX for Logicians pages, so there will be some (temporary) muddle and broken links, etc.
The post Latex pages appeared first on Logic Matters.
October 7, 2024
Book note: Kunen, Foundations of Mathematics

Finally, here’s the last book in my ‘must-revisit’ stack! — Kenneth Kunen’s The Foundations of Mathematics (College Publications, 2009). Now, I’m going to avert my gaze from some of the philosophical asides here. Kunen writes, for example,
Presumably, you know that set theory is important. You may not know that set theory is all-important. That is:
All abstract mathematical concepts are set-theoretic.All concrete mathematical objects are specific sets.Abstract concepts all reduce to set theory.
Really? Really? … Well, fortunately you don’t at all need to buy into such obiter dicta (or into the brief philosophical Ch. III) to find some of Kunen’s technical expositions interesting and helpful.
Ch. 1 (77 pp.) is on set theory, shaped by presenting the axioms of ZFC, unfolding their content and significance, getting as far as talking about ordinals and cardinals, choice, the role of the axiom of foundation, etc. This is clearly done: the chapter could suit mathematicians already a little familiar with sets-in-use from their algebra or topology courses, and/or will make a sharp and useful follow-up — one step more sophisticated but still relatively elementary — if tackled after an entry-level set-theory introduction like Enderton’s.
Ch. 2 (100 pp.) discusses some model theory and proof theory. But, in headline terms, I really didn’t find this chapter as accessible and helpful as the previous one.
Ch. 4 (50 pp.) is on recursion theory. And here a key link is made with the first chapter by construing the inputs and outputs of computable functions as hereditarily finite sets. This is a neat device that puts us in the neck of the woods explored by Melvin Fitting’s lovely book Incompleteness in the Land of Sets. And in fact, you’ll probably get much more out of tackling interesting Kunen’s chapter by reading Fitting first (as well as a more conventional introduction to recursion theory).
In briefest terms, the first and last chapter are, I think, recommendable.
And here I’ll pause the flurry of book notes on some relatively introductory logic texts. As I said before, these have really been written as aides memoires for myself, as I start thinking about the next edition of the Beginning Mathematical Logic Study Guide. But I find that if I make the effort to turn telegraphic jottings into posts here, it does help considerably to concentrate the mind and fix ideas. So make of these recent posts what you will!
The post Book note: Kunen, Foundations of Mathematics appeared first on Logic Matters.
October 5, 2024
On de Swart’s Philosophical and Mathematical Logic

I have mixed feelings about Harrie de Swart’s Philosophical and Mathematical Logic (Springer, 2018). For this long book really is a strange mish-mash, supposedly aimed at philosophers. There are chapters (not very good) on e.g. the philosophy of language and “fallacies and unfair discussion methods”, and e.g. a section on social choice theory. Then there are chapters more directly relevant to the Guide, particularly on propositional and predicate logic, and on intuitionistic logic. Let’s concentrate on those.
If the overall structure of the book is a bit of a disorderly hodgepodge, so too can be the structure of individual chapters. Take, for example, the chapter on propositional logic. We get a bit of baby-logic level talk about truth-functions, then suddenly a compactness argument. Then we are back to baby-logic on defining inferential validity. Some remarks on enthymemes are followed by a bit of metalogic. We get an untidily-presented Hilbert-style proof system (the typography of this book is often clumsy). Then there is what is marked as a digression on a natural deduction system, too quick to be useful. Next we get Beth/Fitting tableaux and a completeness proof for them (but sadly not ideally well-presented, which is a great pity as it makes the treatment of tableaux in later chapters that bit less accessible ). The chapter finishes with a random walk through some paradoxes, and then some arm-waving history in a strange chronology. Frankly, what a presentational mess!
The ramble round propositional logic is followed by a so-so chapter on sets, finite and infinite. And then we are onto predicate logic. Now, this chapter on FOL has — by my lights — a very nice feature: de Swart notationally distinguishes constants from ‘free variables’ from ‘bound variables’ as three different types of symbols, and defines terms as built (ultimately, perhaps using function expressions) from constants and/or free variables alone. This enables him to sidestep that annoying fussing about allowable substitutions and about unwanted variable capture that arises if we take the conventional line and have an initially undifferentiated class of variables, and we get nice tableaux rules etc. I’m rather minded in the Guide to say enough about Beth/Fitting tableaux to make the discussion in de Swart’s propositional logic chapter rather more accessible, and then I can recommend those sections plus this chapter on FOL as pretty useful.
Taking up the tableaux theme again, I can then also recommend the chapter on intuitionistic logic which (as noted in an earlier version of the Guide) gives a pretty nicely explained account of one way of doing tableaux for this logic — even if this chapter is still not my ideal presentation of intuitionistic logic. (The ideal short book has yet to be written!)
As for the rest of de Swart’s book? It must sound very ungrateful to say that someone who has written ten chapters adding up to well over five hundred pages would have done better to write a much more focused, more disciplined (but at points more expansive) book of less than half the length. But I’m afraid that that has to be my summary verdict.
The post On de Swart’s Philosophical and Mathematical Logic appeared first on Logic Matters.
October 4, 2024
Van Gogh: Poets & Lovers

Such is the title of the new Van Gogh exhibition at the National Gallery in London. “Over just two years in the south of France, Van Gogh revolutionised his style in a symphony of poetic colour and texture. He was inspired by poets, writers and artists. We look at this time in Arles and Saint-Rémy as a decisive period in his career. His desire to tell stories produced a landscape of poetic imagination and romantic love on an ambitious scale.”
We haven’t been to the exhibition yet. But we have already bought the accompanying book — a typically beautiful production from Yale University Press. These were the years of sunflowers, starry nights, wheatfields and cypresses, olive trees, interiors with those iconic chairs: so many familiar paintings are brought together. And I’ve now read most of the essays in the book with considerable enjoyable (and enlightenment). The tortured soul of romantic myth is quietly downplayed — we learn much more (or at least I learnt more) of Van Gogh’s influences, those writers and poets as well as other artists. And learn too (the revelation to me) of just how he conceived of groups of paintings as essentially related to each other — for example, belonging together in the décoration of the Yellow House in Arles.
I can really warmly recommend the book — a consolation and delight if you are far away and unable to get to the exhibition, and an inspirational preparatory guide if you can later get there.
The post Van Gogh: Poets & Lovers appeared first on Logic Matters.
October 2, 2024
Revisiting Bell & Machover
I had on my desk — or rather, standing in a row under my desk so as not to topple over — a stack of books that I wanted to read/revisit before the end of September, as preparation for revising the Study Guide (particularly the chapter on FOL). There are two books from that stack which I haven’t mentioned yet. I really want to move on, so I’ll be brief and briefer than the books really deserve. But I don’t feel too bad about this because — in at least enough parts! — I can be quite positive.
So first, in this post, let me wind the clock right back and quickly revisit a classic book from another era, which oddly doesn’t feature either in the current version of the Study Guide or in its Appendix of book notes on major wide-ranging texts on mathematical logic.

Once upon a long time ago, John Bell and Moshé Machover ran a notable one-year masters-level programme on mathematical logic and the foundations of mathematics at London University. They then developed their lecture notes into A Course in Mathematical Logic published by North-Holland in 1977. This is a very substantial book of 599 pages, and a major achievement in its time, rightly well-regarded back in the day.
But, almost fifty years on, the question inevitably arises: what does it have to offer the reader today compared with more recent texts (in particular, how well is it likely to work for a student launching into a course of self-study?).
As the authors note, various parts of the Course had their origins in different lecture courses, and they can often be tackled independently of each other. For example, you don’t need to know the particular details of Bell and Machover’s account of FOL in order to cope with their later discussion of formal arithmetics. It is therefore quite reasonable to chunk up the book into discrete parts, and to assess these separately. So that’s what I’ll do.
Chs 1–3, Propositional and first-order logic (pp. 124). There is a lot to like about the first chapter here — in particular the way that both tableaux and axiomatic systems are introduced and interrelated. (Unsigned) tableaux are nicely motivated immediately after the truth-functional semantics for the basic connectives is defined (and we get a proof too that a version of excluded middle could be conservatively added as a tableaux rule). Soundness and a (weak) completeness theorem for tableaux are snappily proved. Then we meet a Hilbert-style proof system, and it is shown directly (i.e. by syntactic proof-manipulations) that this warrants the same deductions as the tableaux system, establishing that the new proof system is complete too. Then we get a direct proof of weak completeness for our Hilbert system by Kalmar’s method, and a direct proof of strong completeness by Zorn’s Lemma and the construction of maximal consistent sets. This could be very useful reading for many, drawing various ideas together and showing how they interrelate.
But I can’t in the same way recommend the similarly structured chapters on FOL. Although they start well enough, the semantic story about FOL — in particular when it comes to a laboured discussion of substitution — soon becomes rather too heavy-handed, and the version of a tableau system for FOL is far from the nicest.
Ch. 4, Boolean algebras (pp. 36) This is a nice stand-alone chapter, and it still makes a recommendable introductory account — especially §§1–5.
Ch. 5, Model theory (pp. 65) Somewhat action-packed, and lacking some of the helpful classroom asides we find in earlier chapters. There are now more accessible treatments of elementary model theory.
Chs 6–8, Recursion theory and arithmetic (pp. 174) Once upon a time, this group of chapters would have been particularly interesting in virtue of its early account of the then relatively-recent MRDP theorem and the use of that theorem in proving further key results. Still pretty readable, but this is a topic area with some wonderful alternative texts. Though for one alternative option on recursion theory and arithmetic, we should certainly note Machover’s more approachable reworking of some of the same material in his own later, shorter, book (though he doesn’t actually prove the MRDP theorem there, referring back to the details here).
Ch 9, Intuitionistic first-order logic (pp. 59). There is a useful initial motivating discussion in §§1-4. But we don’t get the clearest of accounts of how the Beth/Fitting tableaux system which is introduced next is supposed to work: de Swart in his chapter on intuitionism, for example, does better. And the rest of the chapter doesn’t give e.g. the nicest introduction to Kripke semantics either. So not the place to start.
Ch. 10, Set theory (pp. 72). After more routine introductory sections, the remaining sections — including §5 on reflection principles, §7 on absoluteness, §8 on constructible sets, §9 on the consistency of AC and GCH — could well still be useful supplementary reading for those who already know some elementary set theory. But of course there are many alternatives!
Ch. 11, Non-standard analysis (pp. 45). This chapter is a sophisticated but somewhat opaque treatment, a level or two up from most of what has gone before, and rather too remote from the accessible but intriguing entry-level considerations we usually meet in introductory accounts of Robinson-style constructions. Certainly not for the faint-hearted.
Summary verdict An exceptional book in its day, still worth revisiting in part.
The post Revisiting Bell & Machover appeared first on Logic Matters.
September 30, 2024
Two shorter book notes

Yuri Manin who died last year was a seriously distinguished mathematician, being — for instance — one of the first recipients of the Schock Prize for mathematics. His interests ranged very widely, from algebra and topology to quantum field theory. So A Course in Mathematical Logic for Mathematicians (1977 translation, Springer) is written by an author with an usually broad background which interestingly shows through from time to time in the book.
The Preface starts: “This book is above all addressed to mathematicians. It is intended to be a textbook of mathematical logic on a sophisticated level, presenting the reader with several of the most significant discoveries of the last ten or fifteen years. These include: the independence of the continuum hypothesis, the Diophantine nature of enumerable sets, the impossibility of finding an algorithmic solution for one or two old problems.” So, yes, this is indeed aimed at pretty competent mathematicians. And yes, the attraction of the book when it appeared was that it gave early textbook accounts of e.g. Boolean valued models in set theory, or of the MRDP theorem.
Almost fifty years on, there are — quite unsurprisingly — more accessible accounts to be had of those then-much-more-recent results. And the level of discussion can be, well, ‘sophisticated’. So Manin’s book isn’t, whether in whole or in part, really a candidate for primary recommendations in the Beginning Mathematical Logic Study Guide. Still, it is distinctive enough that it should probably get a mention as being of possible interest to enthusiasts who find its style congenial. Indeed, I thought it did get just such a mention in earlier versions of the Guide; but it turns out that my memory plays me false.

A book I do mention in the current Guide is Volume II of George Tourlakis’s Lectures, i.e. the volume on set theory (I was probably unnecessarily polite about it!). But what about Volume I (CUP, 2003)?
This has two long chapters. The first (204 pp.) is called ‘Basic Logic’. We get an account of first-order languages, a Hilbert-style proof system (with all instances of tautologies as axioms), soundness, completeness and compactness proofs, and a little model theory (including e.g. the Loś-Vaught test and something about infinitesimals). Then we learn about computability and recursive functions, leading to semantic and syntactic versions of the first incompleteness theorem. The menu of topics is a standard one, then. But I just can’t bring myself to warm to the way the exposition goes, especially when it comes to Gödelian incompleteness. There are, in summary terms, much better options available.
The second chapter (116 pp.) is called ‘The Second Incompleteness Theorem’. The blurb advertises this as “the first presentation of a complete proof of Gödel’s second incompleteness theorem since Hilbert and Bernay’s [sic] Grundlagen” (but cf. Adamowicz/Zbierski 1997?). To my mind, Tourlakis’s presentation hacks through a mass of detail in a way that just isn’t going to engender much understanding at all. Stick e.g. to Rautenberg.
The post Two shorter book notes appeared first on Logic Matters.



