Skipping past five books …
I said at the end of the last post that I was going to return to discuss Smullyan’s Further Guide. But having looked at it again more closely, I’m inclined to think this book is really a bit too idiosyncratic to get more than a passing mention in the Logic Matters Study Guide. So on second thoughts I’ll say no more about it here. Which isn’t at all to deny that Smullyan’s book would be intriguing and challenging for the right reader.
One of the parts of the Study Guide I’m most concerned to improve in a second edition is the coverage of FOL; hence my (re)visiting a raft of relatively elementary texts to see what alternative/additional recommendations I might offer. Here, for the record, are three books which are broadly quite conventional and — looking back at some notes, and dipping in again — I simply judge to have nothing distinctive to recommend them in coverage and/or approach compared with other treatments of the same familiar material. Michał Walicki’s Introduction to Mathematical Logic (World Scientific, 2012, 268 pp.) is marred by bad English and is also unbalanced on PL vs FOL. Robert L Causey’s Logic, Sets and Recursion (Jones and Bartlett, 2nd edn. 2006, 512 pp.) strikes me as tedious. José Zalabardo’s Introduction to the Theory of Logic (Westview, 2000, 330 pp.) is better, but the technical presentations can be quite dense.
A level or two up from those three books, there is an earlier and more mathematically flavoured book by Zofia Adamowicz and Paweł Zbierski, Logic of Mathematics (Wiley 1977). This is a serious text; but it is often significantly harder work and less reader-friendly than many of the alternatives.
In a bit more detail, after a very brief introduction, the Logic of Mathematics has two parts. The first part (135 pp.) is an introduction to FOL, with an emphasis on model-theoretic ideas (so we start with discussions of mathematical structures, maps between structures, etc., before meeting first-order languages designed to talk about such things). There’s a standard axiomatic system, and a Henkin completeness proof. We get as far as defining ultraproducts and giving a direct proof of compactness using ultraproducts without going via completeness. All fine, but not distinctively inviting.
The second part of the book (105 pp.) starts with three chapters around and about the first incompleteness theorem, starting from a proof that the primitive recursive functions are representable in PA by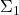 
formulas. But this lovely topic is just not made as engaging as it should be. A fourth chapter then gives a decidedly opaque treatment of the second incompleteness theorem.
The book finishes with three ambitious chapters, one on the independence of Goodstein’s Theorem, one on Tarski’s result that the theory of ordered real closed fields admits the elimination of quantifiers and hence is complete, and one on Matiyasevich’s Theorem. Credit to Adamowicz and Zbierski for tackling these, but I can only report that in each case much more accessible discussions are available elsewhere.
True, these various negative headline judgements are rather peremptory; but then as I’ve said before the whole point of the Study Guide project is to make discriminations. So, moving on again, …
The post Skipping past five books … appeared first on Logic Matters.
