Book note: Marker, An Invitation to Math. Logic, III

Part III of Marker’s book gives us a 63 pp. introduction to the theory of computability. Ch. 9 explores models of computation, first very briskly introducing unlimited register machines. We next meet primitive recursive functions, and then the partial recursive functions. It is then proved that the partial recursive functions are exactly those partial functions computable by a register machine; and we get a bit more evidence for Church’s Thesis by noting that machines with random access memory won’t compute more. The chapter — under 20 pages before the Exercises start — ends with a very quick glance at Turing machines.

So this all proceeds at a breathless pace. There are just three sides on URM machines, just two on Turing machines. The reader is left to work out the motivation for the official definition of a primitive recursive function from the examples that actually follow that definition. Again, the move from primitive recursive to partial recursive functions is done at pace (and after just a page, we immediately meet an Ackermann-style function as an example of an intuitively computable and total recursive but not primitive recursive function). None of the ideas thus far are hard, of course: but there are some quite excellent, rather less breathless and hence more illuminating, alternative treatments available.

Similar remarks apply to the next two chapters. Ch. 10 is on universal machines and undecidability. It is shown that there is a universal computable functions 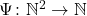such that if 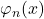is 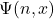, then 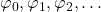is an enumeration of all the computable (one-place) partial functions. We meet Kleene’s T-predicate, the s–m–n theorem, then the unsolvability of the halting problem leading to the undecidability of first-order validity. And next it is on to Rice’s theorem and the (second) Recursion Theorem — with all this in the space of just 11 pages! Really?

Then Ch. 11, only a couple of pages longer, discusses computably enumerable sets, many-one reducibility, computably inseparable sets, the arithmetical hierarchy, Kolmogorov randomness and more. To be frank, I see nothing to be gained by rushing through at this pace. Setting aside the very last topic, the beginner — and especially one engaged in solo self-study — will assuredly get a better conceptual  understanding of what is going on by tackling, e.g., the more expansive early chapters of Cutland’s classic text instead of these three rushed chapters by Marker.

Now, Chs 9 to 11 may fly by at unhelpful speed, but the topics covered there are, we can readily agree,  entry-level. By contrast, Ch. 12 on Turing Reducibility rachets up the level of sophistication significantly — it is still only 14 pages, yet we get as far as Friedburg-Muchnik (which e.g. Cutland says is beyond the scope of his book, but which is proved by Cooper in his more advanced text but not starting until his p. 238) and the Low Basis Theorem (Cooper p. 330). Assuming you come primed with a strong enough understanding of basic computability theory, you could perhaps usefully tackle this chapter (these upper-level topics are of course intrinsically interesting).  But again my sense is that the slower presentation of Friedburg-Muchnik in Cooper (say) is much more likely to engender a deeper understanding of the priority method used in the proof.

So, a summary verdict on Part III: too much is done too quickly for a first encounter with this material. Of course, this could be useful revision/consolidation material for enthusiasts who like Marker’s brusque style; though, by my lights, there are more attractive alternatives for that too.

The post Book note: Marker, An Invitation to Math. Logic, III appeared first on Logic Matters.