Peter Smith's Blog, page 79

Excluded middle, harmony, intuitionist logic for beginners

In the first two chapters on propositional natural deduction for my revised logic text — coming quite a way into the book — I start with a system for conjunction, disjunction and negation. There are the usual pairs of introduction/elimination rules for conjunction and disjunction. There are three rules for negation, (RAA) — a subproof from A to ★ proves not-A; (Abs) — from A and not-A derive ★; and (DN), the usual double negation rule. ‘★’ is an absurdity marker not a falsum wff. (EFQ) — from absurdity, anything — is a derived rule, but not one of the three basic rules. We note that (RAA) and (Abs) can be thought of as another harmonious pair of introduction/elimination rules, leaving (DN) an odd one out. (Rules for the conditional are introduced in the third chapter.)

The first chapter on natural deduction motivates/introduces the rules by talking through some worked examples. The second chapter looks at some issues, about explosion, the best disjunction elimination rule, vacuous discharge, etc, and takes with another look at the negation rules. First, we note equivalents to (DN), including (EM), excluded middle. Then — at the very end of the chapter — I briefly touch on the status of (DN)/(EM).

I want to say something about this last issue. But equally, in the context of an introductory book I can’t say much. Here below is a draft of the relevant page-and-a-half. I’d very much welcome comments (perhaps not so much about philosophical doctrine, as about the expositional clarity given the intended audience! — can I put things better?).

In §21.4, we noted that the negation rules (RAA) and (Abs) make a nicely harmonious introduction/elimination pair. Which leaves the remaining negation rule (DN) and its equivalents out on a limb. As we asked before: what, if anything, is the significance of this? The issues here quickly become complex and contentious; but here are a few introductory remarks.

We ordinarily distinguish being true from being warrantedly assertible. The naive thought is that whether a proposition is true depends on how the world is — and how the world is may be beyond our ken, even in some cases beyond our capacity to find out. Hence, we suppose, a proposition can be true without there being any available warrant or grounds for justifiably asserting it.
But on reflection, for some classes of propositions, perhaps there is after all no more to being true than being warrantedly assertible. So-called ‘intuitionists’ and other constructivists hold that mathematics is a case in point. Mathematical truth, they say, does not consist in correspondence with facts about objects laid out in some Platonic heaven (what kind of objects could these be? how could we possibly know about them?). Rather, being mathematically true is a matter of being warrantedly assertible on the basis of a proof.
We can’t discuss here whether an intuitionist view of mathematics is actually right. But we can ask: what should be our principles of correct informal reasoning if we accept such a view? For the intuitionist, correct inferences in mathematics are those inferences that preserve warrant-to-assert-on-the-basis-of-proof. Which inferences involving the connectives are these?

If you have a warrant for A and have a warrant for B, then you surely have a warrant for their conjunction, A and B. Likewise, having a warrant for A (or equally, a warrant for B) is enough to give you a warrant for A or B, when the ‘or’ is inclusive. And if you can show that supposing A leads to absurdity, that is enough to put you in a position to justifiably reject A, i.e. to give you a warrant for not–A.

So even if we are thinking of good inference as a matter of preservation of warranted assertibility, versions of the now familiar introduction rules for the three connectives — with (RAA) as negation-introduction — will still apply. And since the harmonious elimination rules simply allow us to extract again from a wff what the introduction rule for its main connective required us to put in, the elimination rules will continue to apply too.
What, however, will be intuitionist’s attitude to the rule that we can cancel double negations or to equivalent rules? Take the law of excluded middle. The intuitionist won’t deny this (by the rules he accepts, not-(A or not-A) implies both not-A and not-not-A, and hence implies a contradiction). However, the intuitionist won’t endorse excluded middle as a generally applicable principle either. Suppose that A is a mathematical claim that is neither provable nor refutable. Then, according to the intuitionist who holds that all there is to truth in mathematics is provability, we have no warrant to suppose that mathematically things are one way or the other with respect to A, so no warrant for A or not-A.
Now going formal again, imagine you are an intuitionist who wants to encapsulate the inference rules you accept into a variant of our natural deduction system. Then you will adopt all the same rules as our PL system minus (DN) (since that’s equivalent to the unwanted excluded middle). Such a system, at least once we add the rules for the conditional too, is said to define intuitionistic propositional logic. And arguably, this intuitionistic logic is the right formal logic for arguing with the connectives when dealing with any domain where truth is warranted assertability/provability.
Imagine alternatively that you conceive of truth in a more naively ‘realist’ way for some domain. So you think of the truth-values of (non-vague) propositions of the relevant kind as being determined one way or another by the world, independently of whether we can warrantedly judge whether they are true or false. You will then think of negation here in the classical way, as simply swapping the value of a proposition, taking you from a determinately true proposition to a false one and vice versa; and every proposition of the relevant kind determinately has one value or the other, ensuring that excluded middle always holds. Going formal, you will therefore adopt (EM) or equivalently (DN) as one of your rules for the connectives. The classical logic of our PL system reflects that classically realist view of truth.

So, at any rate, goes one often-told story. But it goes without saying that there is a great deal to wrestle with here. Does the apparently attractive logic of PL, with its immediately appealing rules, really presuppose a particular realist conception of truth? Are there really areas of enquiry where the appropriate notion of truth is non-realist, more akin to an idea like ‘warranted assertability’ or ‘provability’. If there are, is intuitionist logic really the right logic for such domains? Does it then make sense to think of different logics as being appropriate to different domains? Or should we rather think of the law of excluded middle — if it doesn’t apply to reasoning in general — as not part of core logic at all? Should we perhaps think of excluded middle, when it applies, as really more like a very general metaphysical claim about the determinacy of some parts of the world?

It also goes without saying that we can’t begin to tackle such intriguing but baffling issues in this book!

And there the chapter will end, apart from the usual end-of-chapter summary and exercises. As I said, all comments (or rather, all comments which bear in mind the intended introductory role of these remarks) will be very gratefully received!

The metaphysics of logic?

A collection of essays on The Metaphysics of Logic, edited by Penelope Rush, was published as a very expensive haddock — no, no, you idiot spell-checker, hardback — in 2014. Even with my large discount as a CUP author, I balked at the price. But it is now newly available as a paperback, and (I confess, without looking too closely) I picked up a copy the other day.

I can’t honestly recommend that you do the same.

At my not-so-tender years, I’m just not very willing to spend my limited time reading papers that are badly written or  unclear where they are going. So I didn’t get very far with the first two pieces in the collection, by Penelope Rush herself and by Jody Azzouni.

The next paper by Stewart Shapiro is predictably three steps up in terms of clarity, focus, and lightness of touch. He is writing about ‘Pluralism, relativism and objectivity’. But if you have read his interesting 2014 book Varieties of Logic then you won’t find much new here.

There follows a typically thought-provoking paper by the late Solomon Feferman on his so-called conceptual structuralism. But it is available on his website here: Logic, mathematics and conceptual structuralism.

Penelope Maddy follows with ‘A second philosophy of logic’, again written with her characteristic clarity. But as with Shapiro’s paper, if you have been keeping up with this  author’s recent work, there will be no surprises. Maddy herself says that the paper “reworks and condenses the presentation” of Part III of her earlier book Second Philosophy. So while the paper here might serve some as a useful introduction to her thinking, it doesn’t really add anything new.

The next paper is at least new, but I’m not sure what other virtues it has. Curtis Franks is out to defend the idea that ‘logic, in the vigor and profundity that it displays nowadays, does and ought to command our interest precisely because of its disregard for norms of correctness’. So he aims to ‘lead the reader around a bit until his or her taste for a correct logic sours’. (Note the ‘a’.) Well, the therapy didn’t work on this reader (though there some interesting but hardly original remarks on the relationship of classical and intuitionist logic). But you can try for yourself here: Logical nihilism.

There follows a piece by Mark Steiner on ‘Wittgenstein and the covert Platonism of mathematical logic’. Wittgenstein seems to make both radical criticisms of classical ideas and to want to leave everything as it is. Steiner explores how to reconcile these tendencies.  Just how much you get out of this will depend on how much residual interest you have in Wittgenstein on the philosophy of the mathematics-he-really-seems-not-to-have-known-much-about.

And that’s all the papers in the first part of the collection, ‘The Main Positions’. These are  all papers by old hands, Rush apart, who have already contributed books on logic and foundations of mathematics. It would have been much more interesting to hear new takes on old positions from younger philosophers.

The next part of the book consists on four random papers cobbled together under the catch-all ‘History and Authors’. The only interesting one is Sandra Lapointe writing about Bolzano’s Logical Realism.

Finally we have three papers on ‘Specific issues’ (now the editor is really struggling to find an organising principle for her heap of contributions). Graham Priest has a short and thin piece on Revising Logic. Jc Beall, Michael Hughes, and Ross Vandegrift contribute another short paper, on Glutty theories and the logic of antinomies (how is this relevant to the volume? — ‘We shall argue that [the logic] LA reflects a fairly distinctive set of metaphysical and philosophical commitments, whereas LP, like any formal logic, is compatible with a broad set of metaphysical and philosophical commitments’). Finally, Tuomas Tahko writes on The Metaphysical Interpretation of Logical Truth: you’ll only like this paper if you think there is anything to be said for slogans like ‘A belief, or an assertion, is true if and only if its content is isomorphic with reality.’ Which I don’t.

So a pretty disappointing collection, one way or another. Save your pennies for some good haddock.

A little writing about writing

A while back — a distressingly long time ago, actually, as it seems like only the day before yesterday — I wrote a couple of pages (linked here)  primarily aimed at beginning graduate students. One was on developing a decent and effective writing style, the other was about getting published; both were based on sessions I’d given a few times in a ‘graduate training programme’.

Rereading them, I thought the page about getting published managed to now look both banal and in certain respects rather dated. And I’m now too out of the swim to want to improve and update it, so I’ve dropped the link.

But general advice on writing surely doesn’t date in quite the same way, and I still quite like the page I first wrote a dozen years back. So I’ve tinkered with it a bit (and followed my own advice in trimming it down where possible). Here’s the latest version. Comments welcome — also, I’d like to link to other people’s similar pages of advice if you have any particular favourites to recommend.

What I didn’t add was a warning about how much time getting from acceptably written to quite well written can take! Reworking my intro logic book involves writing some new chapters. It seems to take me as long to get the prose in a state I’m happy with as to fix the actual contents of a chapter in a late draft. On the other hand, there is real pleasure to be had when things do click into place. The polishing stage can be mightily frustrating and rewarding at the same time.

The Pavel Haas Quartet at the Wigmore Hall (and on BBC)

Pavel Haas Quartet – Pavel Nikl
Photo: Marco Borggreve

Up to the London to go to another Pavel Haas Quartet concert. They played Igor Stravinsky’s short Concertino for String Quartet (new to me, and I’ll need to listen again to get more out it), followed by a wonderful performance of the Ravel quartet. After the interval, the Pavel Haas were joined by Pavel Nikl — who was their original violist, and only left the Quartet early last year for reasons of family illness. They played Dvořák’s String Quintet in E flat major, Op 97, to rapturous applause — indeed an appropriate response. They have recently recorded this Quintet (together with the Dvořák Piano Quintet — the CD is released soon); the music was very obviously in their hearts and in their fingers, and was played with great warmth and their usual stunning ensemble.

Although it isn’t the same as being there, you can listen to the concert for another four weeks on the BBC site, here.

Trinity Poets

The answer to the quiz question? The first group, from George Herbert on, unlike members of the second group, might keep company together in an anthology of poets who were all members of Trinity, Cambridge. OK, if you are fussy, it might be stretching a point, I suppose, to count the versifying A.A. Milne as a poet: but let’s be ecumenical, as his verse certainly has added to the gaiety of nations!

And, yes, a substantial anthology of Trinity Poets has recently been published by Carcanet, edited by Adrian Poole and Angela Leighton. It features almost fifty poets from the sixteenth to the twenty-first centuries, many familiar, but also quite a few new to me. Like many a poetry anthology, it affords the delight of serendipitous discovery. Not least among the most recent poets. So while this is a book I bought with a certain self-mocking collegial devotion, I found myself dipping into it with considerable unforced pleasure.

A literary quiz

Until more logical inspiration strikes, a literary quiz question for you.

Where might George Herbert, Andrew Marvell, John Dryden, Lord Byron, Alfred Lord Tennyson and A. E. Houseman keep company with A. A. Milne and Vladimir Nabokov? And why haven’t John Donne, John Milton, Alexander Pope, Percy Bysshe Shelley, Robert Browning or John Betjemann been invited?

Answer in the next post.

Chiaroscuro: in dark times, some light

Dark times, in many too ways. Words can fail us. But Haydn’s inexhaustible humanity can be a comfort and inspiration, no? So let me recommend a recent CD of his music that I have so very much enjoyed, the Chiaroscuro Quartet returning to the Opus 20 quartets to complete their recording (BIS 2168 — you can also stream through Apple Music, and find their previous four discs there too).

Four friends, occasionally coming together to play concerts and record, performing with delight and bold inventiveness. Their use of gut strings makes for wonderful timbres, now earthy, now confiding, now echoing a viol consort. This is extraordinary playing, and not just from Alina Ibragimova who leads the quartet: the sense of ensemble and the interplay of voices puts some full-time quartets to shame. Richly rewards repeated listening.

OUP philosophy book sale

In case you missed an announcement, OUP has a sale offer on philosophy books with 30% off across the board. (Go to the OUP site, click on the left at the top of the menu “Academical and Professional”). Neil Tennant’s brand new Core Logic which I mentioned in the last post is available, of course. And forthcoming books which I am looking forward to, which are likely to be of interest to readers of Logic Matters, include

Elaine Landry, Categories for the Working Philosopher (Nov 2017).
Geoffrey Hellman and Stewart Shapiro, Varieties of Continua: From Regions to Points and Back (Jan 2018).
Tim Button and Sean Walsh, Philosophy and Model Theory  (Feb 2018).

Enthusiasts for category theory may also be interested in Olivia Caramello’s book

Theories, Sites, Toposes: Relating and studying mathematical theories through topos-theoretic ‘bridges’ (Nov 2017) — though I have in the past found it difficult to grasp her project, which sounds as if ought to be of interest to those with foundational interests.

All these books are available for pre-order in the sale.

Core Logic

The revised, surely-more-natural, disjunction elimination rule mentioned in the last post is, of course, Neil Tennant’s long-standing proposal — and the quote about the undesirability of using explosion in justifying an inference like disjunctive syllogism is from him. This revision has, I think, considerable attractions.  Even setting aside issues of principle, it should appeal just on pragmatic grounds to a conservative-minded logician looking for a neat, well-motivated, easy-to-use, set of natural deduction rules to sell to beginners.

But, in Tennant’s hands, of course, the revision serves a very important theoretical purpose too. For suppose we want to base our natural deduction system on paired introduction/elimination rules in the usual way, but also want to avoid explosion. Then the revised disjunction rule is just what we need if we are e.g. to recover disjunctive syllogism from disjunction elimination. And Tennant does indeed want to reject explosion.

Suppose, just suppose, that even after our logic teachers have tried to persuade us of the acceptability of explosion as a logical principle, we continue to balk at this — while remaining content e.g. with the usual remaining negation and conjunction rules. This puts us in the unhappy-looking position of accepting the seemingly quite harmless 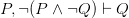and 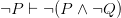while wanting to reject 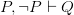. So we’ll have to reject the unrestricted transitivity of deduction. Yet as Timothy Smiley put it over 50 years ago, “the whole point of logic as an instrument, and the way in which it brings us new knowledge, lies in the contrast between the transitivity of ‘entails’ and the non-transitivity of ‘obviously entails’, and all this is lost if transitivity cannot be relied on”. Or at least, all seems to be lost. So, at first sight, restricting transitivity is a hopeless ploy. Once we’ve accepted those harmless entailments, we just have to buy explosion.

But maybe, after all, there is wriggle room (in an interesting space explored by Tennant).  For note that when we paste together the proofs for the harmless entailments we get a proof which starts with an explicit contradictory pair 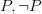. What if we insist on some version of the idea that (at least by default) proofs ought to backtrack once an explicit contradiction is exposed, and then one of the premisses that gets us into trouble needs to be rejected? In other words, in general we cannot blithely argue past contradictions and carry on regardless. Then our two harmless proofs cannot be pasted together to get explosion.

But how can we restrict transitivity like this without hobbling our logic in the way that Smiley worried about? Well suppose, just suppose, we can arrange things so that if we have a well-constructed proof for 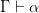and also a well-constructed proof for 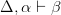, then there is EITHER a proof of 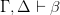(as transitivity would demand) OR ELSE proof of 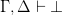. Then perhaps we can indeed learn to live with this.

Now, Neil Tennant has been arguing for decades, gradually revising and deepening his treatment, that we can arrange things so that we get that restricted form a transitivity. In other words, we can get an explosion-free system in which we can paste proofs when we ought to be able to, or else combine the proofs to expose that we now have contradictory premisses (indeed that looks like an epistemic gain, forcing us to highlight a contradiction when one is exposed). On the basis of his technical results, Tennant has been arguing that we can and should learn to live without explosion and with restricted transitivity (whether we are basically classical or intuitionist in our understanding of the connectives). And he has at long last brought everything together from many scattered papers in his new book Core Logic (just out with OUP). This really is most welcome.

Plodding on with my own book, I sadly don’t have the time to comment further on this Tennant’s book for now. But just one (obvious!) thought for now. We don’t have to buy his view about the status of core logic (in its classical and constructivist flavours) as getting it fundamentally right about validity (in the two flavours). We can still find much of interest in the book even if we think of enquiry here more as a matter of exploring the costs and benefits as we trade off various desiderata against each other, with no question of there being a right way to weight the constraints. We can still want to know how far can we go in preserving familiar classical and constructivist logical ideas (including disjunctive syllogism!) while avoiding the grossest of “fallacies of irrelevance”, namely explosion. Tennant arguably tells us what the costs and benefits are if we follow up one initially attractive way of proceeding — and this is a major achievement. We need to know what the bill really is before we can decide whether or not the price is too high.

A more natural Disjunction Elimination rule?

We work in a natural deduction setting, and choose a Gentzen-style layout rather than a Fitch-style presentation (this choice is quite irrelevant to the point at issue).

The standard Gentzen-style disjunction elimination rule encodes the uncontroversially valid mode of reasoning, argument-by-cases: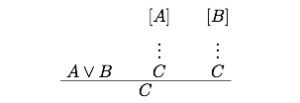

Now, with this rule in play, how do we show 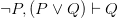? Here’s the familiar  line of proof: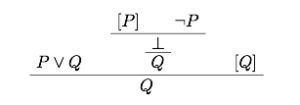But familiarity shouldn’t blind us to the fact that there is something really rather odd about this proof, invoking as it does the explosion rule, ex falso quodlibet. After all, as it has been well put:

Suppose one is told that A B holds, along with certain other assumptions X, and one is required to prove that C follows from the combined assumptions X, A B. If one assumes A and discovers that it is inconsistent with X, one simply stops one’s investigation of that case, and turns to the case B. If C follows in the latter case, one concludes C as required. One does not go back to the conclusion of absurdity in the first case, and artificially dress it up with an application of the absurdity rule so as to make it also “yield” the conclusion C.

Surely that is an accurate account of how we ordinarily make deductions! In common-or-garden reasoning, drawing a conclusion from a disjunction by ruling out one disjunct surely doesn’t depend on jiggery-pokery with explosion. (Of course, things will be look even odder if we don’t have explosion as a primitive rule but treat instances as having to be derived from other rules.)

Hence there seems to be much to be said — if we want our natural deduction system to encode very natural basic modes of reasoning! — for revising the disjunctive elimination rule to allow us to, so to speak, simply eliminate a disjunct that leads to absurdity. So we want to say, in summary, that if both limbs of a disjunction lead to absurdity, then ouch, we are committed to absurdity; if one limb leads to absurdity and the other to C, we can immediately, without further trickery, infer C; if both limbs lead to C, then again we can derive C. So officially the rule becomes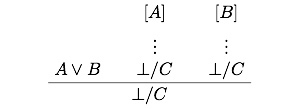where if both the subproofs end in so does the whole proof, but if at least one subproof ends in C, then the whole proof ends in C. On a moment’s reflection isn’t this, pace the tradition, the natural rule to pair with the disjunction introduction rules? (At or at least natural modulo worries about how to construe “” — I think there is much to be said for taking this as an absurdity marker, on a par with the marker we use to close of branches containing contradictions on truth trees, rather than a wff that can be embedded in other wffs.)

If might be objected that this rule offends against some principle of purity to the effect that the basic, really basic, rules for another connective like disjunction should not involve (more or less directly) another connective, negation. But it is unclear what force this principle has, and in particular what force it should have in the selection of rules in an introductory treatment of natural deduction.

The revised disjunction rule isn’t a new proposal! — it has been on the market a long time. In the next post, credit will be given where credit is due. But for now I want the consider the proposal as a stand-alone recommendation, not as part of any larger revisionary project. The revised rule is obviously well-motivated, makes elementary proofs shorter and more natural. What’s not to like?