Peter Smith's Blog, page 83

Going cold turkey

I can’t say I’m surprised that an election has been called. As it becomes clearer and clearer (to the Tories in power — they were warned!)  how horribly long and messy and potentially disastrous the Brexit process will be, you can see why Theresa May, her Chancellor, and the other grown-ups in the room will be hoping and praying for a majority large enough to be able to ignore the madder Brexiteers in their party. We shall see.

And that’s going to be my last word on the whole depressing matter here, at least until after the election. I wasted far too much time reading the political news, the commentaries, the deep background pieces, at referendum time, and again with the Trump election. There was no joy in that and I’m not sure I ended up very much more enlightened about what the hell has been going on with us (instant history is rarely good history). So this time around, it is a self-dying ordinance for me. It is already clear, at least to me, how to cast my solitary vote locally. And so, until the day comes round, no more newspapers on the iPad first thing; no more late-night catch-ups; no more long-reads from political writers. I’m going cold turkey.

Another postcard from Rome

We always like to go to smaller, less-visited places — not just to avoid the teeming crowds, but also because we find that smaller galleries and churches and palazzi can be more humanly interesting and (not feeling overwhelmed) more enjoyable. Three final highlights of our stay have been seeing a fine exhibition Artemisia Gentileschi and Her Times,

visiting the small but stunningly frescoed Oratorio del Gonfalone, and going to the beautiful Villa Farnesina in Trastevere (above) which has frescoes by (among others) Raphael. Even the exhibition wasn’t busy, and we were the only visitors to the Oratorio (used for evening concerts and other events — you knock on a door in the street behind, and we were shown it by the President of the confraternity).  All wonderful.

And for when you’ve finished feeding the soul, a top restaurant recommendation: Pierluigi.

Postcard from Rome

A week or so in Rome, with beautiful sun, some wonderful food, coffees as they should be, quite a lot of wandering around back streets, and a less than frenetic cultural pace visiting a few churches and exhibitions. We arrived just as the not-so-United Kingdom formally triggered the process of leaving the EU. Seems somehow rather appropriate to show our feelings about this folly by leaving the UK for the Eternal City, for however short a time.

I must say that I have found the Brexit absurdities plus the Trump fiasco less than cheering. Though having nothing original or insightful to say about either, I’ve not wanted to bang on about them here. But the political news has been lowering and distracting enough to stem the flow of blog posts for a while. A few more days of sun and noisy civilization, and normal service ought to be resumed. 

A word for our times

TrumpBrexiety (© Lucy Mangan)

Raymond Smullyan (1919–2017)

I first came across Raymond Smullyan’s work — surely  like many of my sort of vintage — through his wonderfully inventive and illuminating short(ish) paper “Languages in which self-reference is possible” which was reprinted in Hintikka’s 1969 The Philosophy of Mathematics (in the Oxford Readings series). Still more than worth reading, after all this time. And that paper led me to look out his First-Order Logic over forty years ago. I think it took me a while to really appreciate that classic: certainly, I kept battling on teaching first-year students Lemmon-style natural deduction for while before I was fully gripped by the loveliness of trees! I had occasion to read the first half of First-Order Logic again a few months ago, and it is such a delight.

But perhaps even more elegant, clear, readable, illuminating, getting-to-the-heart-of-things, there’s Smullyan at his very best in the three Oxford Logic Guides he published in quick succession — Gödel’s Incompleteness Theorems (1992), Recursion Theory for Metamathematics (1993), and  Diagonalization and Self-Reference (1994). They give the lie to G.H. Hardy’s bitter remark that “Exposition, criticism, appreciation, is work for second-rate minds.” Smullyan’s expositions and re-organizations and novel re-appreciations and inventive drawings-out of new connections are surely the work of a first-rate mind.

And then, as a late coda, there is that other great book that Smullyan wrote with Melvin Fitting, Set Theory and the Continuum Hypothesis (1996). Those of us past the first, second, and even third flush of youth can’t but be encouraged and cheered to see Smullyan getting perhaps to the very top of his game, as far as the writing of serious logical texts is concerned, as he moves into his seventies. (The very late books like Logical Labyrinths and A Beginner’s Guide to Mathematical Logic are perhaps too uneven and quirky to really work, but still have fun and instructive episodes.)

I can’t think of a single logician whose writings I have enjoyed reading and working through more than Smullyan’s, and whose elegant lucidity I’d more like to be able to emulate. And there are few logicians that I’ve learnt as much from. So I wanted to mark Smullyan’s passing, as others have, with very warm appreciation and gratitude.

“But what about all the puzzle books? You haven’t mentioned them!” Well, I know that many others have loved them, but I very much prefer my logic served straight up: and I think it would be a sad if Smullyan is mainly remembered for them. I don’t seem to have the kind of mind that is drawn to puzzle books, to magic tricks, or Taoism: but that’s uptight Englishness for you!

The New York Times obituary

Setting tableaux using prooftrees.sty

The first edition of IFL was typeset using FrameMaker (long since defunct on a Mac), so I’m having to LaTeX the second edition from scratch. I’m planning to use Clea Rees’s fairly new package prooftrees.sty for downward-branching tableaux, a.k.a. truth-trees, since this seems to give the right level of control over trees and beat other options by some way.

I have therefore added a link on the LaTeX for Logicians page on tree proofs to a document on setting tableaux using this package. This will contain some notes on using the package, e.g. on how to avoid it clashing with busstrees.sty, and on any useful undocumented tweaks I find. And then I’ll also give a few examples, including some constructed for IFL.

I’d be very happy to hear about any tips and tricks for this package from other users that could also be shared at LaTeX for Logicians. (And of course, all other suggestions and  corrections for L4L are always welcome!)

Since it is Schubert’s birthday ….

Barbara Bonney, soprano; David Shifrin, clarinet; André Watts, piano. Der Hirt auf dem Felsen, “The Shepherd on the Rock”, D. 965

Conditionals again

Here are two draft chapters on conditionals for the second edition of my Introduction to Formal Logic (to replace chapters 14 and 15 of the current edition). I’ve got to the point that I’d very much welcome comments. Note, there will be added exercises which will further explore e.g. the biconditional and further oddities of equating ‘if’ and ‘⊃’.

The main changes? I no longer endorse Jackson’s theory in the way I used to do.  So what positive line do I take? How do I sell the blasted material conditional?

… even if it turns out that ‘⊃’ is not a close analysis of ordinary ‘if’, we can still adopt it to serve as an easily managed, elegantly simple, substitute in formal languages for the messier vernacular conditional. We hereby do so!

In fact, this is exactly how the material conditional was introduced by Frege, the founding father of modern logic, in his Begriffsschrift. Frege’s aim was to construct a formal language in which mathematical reasoning, in particular, could be represented entirely clearly and unambiguously – and for him, such clarity requires departing from “the peculiarities of ordinary language” as he calls them, while capturing some essential logical content. Choice of notation apart, the central parts of Frege’s formal apparatus including the material conditional, together with his basic logical principles (bar one), turn out to be exactly what mathematicians need.

That’s why modern mathematicians – who do widely use logical notation for clarificatory purposes – often introduce the material conditional in text books, and then cheerfully say (in a Fregean spirit) that this tidy notion is what they are officially going to mean by ‘if’. It serves them perfectly in formally regimenting their theories (e.g. in giving axioms for formal arithmetic or set theory). And the rules that the material conditional obeys – like (MP) and (CP) – are just the rules that mathematicians already use in reasoning with conditionals. Much more about this in due course.

This gives us, then, more than enough reason to continue exploring the material conditional. For we will want to investigate what happens when we adopt ‘⊃’ as a ‘clean’ substitute for the conditional in our formal languages, one which serves the central purposes for which we want conditionals, at least in contexts such as mathematics.

For more, do please have a look at the two quite short chapters (I guess anyone teaching or indeed learning logic will have views on the material conditional — I’m trying to be pretty anodyne, so would like to know if I upset too many readers!). As I say, all comments will be most gratefully received.

Serendipitous distractions

So the CUP Book Sale is over for another twelve months — and with changed rules after last year’s unseemly scrums, this year’s Sale was a very much more enjoyable and civilised affair. After a few pretty abstemious visits, I still came away with a dozen books in all, including to my suprise a couple that were on my wish-list from books published in 2016 — George Herbert: 100 Poems (a beautiful book in form and content!) and Bart Jacobs’ Introduction to Coalgebra (for its promise of categorial interest).

Books are put on the sale shelves in a completely random order. So half the pleasure is making serendiptous finds of titles that I could not usually justify buying (even with my press author’s discount and my level of self-indulgence). At £3 for a paperback — only a few pennies more than the Saturday newspaper — how could I resist a little music handbook on The Goldberg Variations?  And I’ve been inspired by the excellent recent BBC film To Walk Invisible to start doing some re-reading of the Brontës; so The Cambridge Companion to The Brontës looks fascinating.

However, the book which I sat down with, a glass or two in hand, and devoured in a sitting later the very day I got it was G. H. Hardy’s A Mathematician’s Apology (with a long introduction by C. P. Snow). I’m not sure that I’ve read this cover-to-cover since I was a schoolboy, and if I ever had a copy it has long since gone astray. It is a strange book in some ways, and a sad one too. But this resonated for me: “When the world is mad, a mathematician may find in mathematics an incomparable anodyne.”  Perhaps not incomparable: there’s always Bach. But losing myself thinking through elegant mathematics, trying to get something really clear in my own mind, and perhaps trying to explain it as best I can to others, certainly works for me. Hardy also wrote, astringently, that “Exposition, criticism, appreciation, is work for second-rate minds.” Perhaps so: but it can keep us second-rate minds happily distracted just for a while from the world’s current madness!

Frege on “if”

I’ve been looking at the passage early in the Begriffsschrift where Frege introduces the material conditional — not, of course, using that label, and not of course with our notation. He notes that 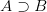can be affirmed when A is denied or when B is affirmed, and in those cases “there need not exist a causal connection between the two contents” (the content of A and the content of B). One can also

make the judgment without knowing whether A and B are to be affirmed or denied. For example, let A denote the circumstance that the Moon is in quadrature [with the sun] and B the circumstance that it appears as a semicircle. In this case  can be translated with the aid of the connective ‘if’: ‘If the moon is in quadrature, then it appears as a semicircle’. The causal link implicit in the word ‘if’, however, is not expressed by our symbols, although a judgement of this kind can be made only on the basis of such a link.

That’s Michael Beaney’s translation, with notation changed: but other translations don’t differ in relevant ways. In particular, they all use the word ‘causal’ in rendering Frege’s remarks. And this is what caught my eye.

For Frege seems to be intending to make general claims here. To judge 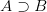  we need not suppose that there is a causal connection or link between A and B, it suffices (of course) to be in a position to deny A or assert B. By contrast, however, a judgement if A then B can only be made on the basis of a causal link. And doesn’t that strike us as an odd line for him to take, given that Frege’s first interest is in the language of arithmetic and the  language of analysis, where causation doesn’t come into it? True arithmetical ‘if’s aren’t causal ‘if’s — or so many of us English-speaking analytic philosophers would be inclined to say (not least because we have read our Frege!).

We might wonder, then about the shared translation here. But the relevant German is “ursächlicher Zusammenhang” and “ursächliche Verknüpfung”; and according to the dictionary ‘ursächlich’ means ‘causal’. So it seems that the translations are right.

Though this sets me musing. In English (or at least, in my corrupted-by-philosophy English) there is something of a disconnect between ‘cause’ and ‘because’. If we have A true and this fact causes B to be true, then I am happy to say B, because A. But this doesn’t reverse: in particular, in mathematical cases where  I am happy to say something of the form B, because A, I’d usually balk at talking about causation. For example, I’m quite happy to say of a particular function that it is computable because it is primitive recursive, but would balk (wouldn’t you?) at saying that its being primitive recursive causes it to be computable.

Now I suppose English could have had the notion of becausal link, more general than a causal connection, i.e. some connection or other that holds when B, because A is true. And then we could imagine the view that “a becausal link is implicit in the word ‘if'” (however exactly we are to spell out ‘implicit’ here).

So that raises a question: when Frege talks about ‘if’s and causal connections, does he in fact mean anything stronger than becausal connections (assuming that a ‘because’ need not be causal ‘because’). How are things in philosophical German? Does “ursächliche Verknüpfung” definitely connote a causal as opposed to, more generally, becausal link?