Peter Smith's Blog, page 76

Onwards!

The twelfth birthday of this blog went by uncelebrated, but I guess it is a milestone of sorts.

While a number of good logic/maths blogs continue flourishing (see the sidebar!), many philosophy blogs do seem to be dropping by the wayside — becoming moribund or (like the long-running philosophy of religion Prosblogion) simply  disappearing. I wonder why philosophers are rather giving up on this relatively easy and relaxed way of talking to each other? Possibly, all the cool kids have moved on to something else (select Facebook groups, perhaps? — though I can’t say that that appeals, and even less so after recent shenanigans). Or very possibly, it’s a reflection of the fact that academic life is getting ever more stressed and time-pressured. I have the luxury of retirement, with no one looking over my shoulder.

Not that there haven’t been times over the last couple of years, with the world seeming to be going to hell in a handcart rather faster than usual, when it has been difficult to muster quite enough enthusiasm to write here about what are, after all, decidedly minor matters. But then, I enjoy being occasionally distracted  by other blogs; and enough people do seem to enjoy coming here to be distracted in their turn.

So onwards! Posts soon on exhibitions of Italian art, on philosophical logic books from back in the day which are worth another look, on the Pavel Haas Quartet (again), on some other quartets, on novels I’ve been (re)reading recently, and even some more logic matters. Well, a chap needs a hobby …

The post Onwards! appeared first on Logic Matters.

Every perceptual experience is possibly delusory

(A) Take the following familiar kind of philosophical claim:

Every perceptual experience is possibly delusory!

How do you read this? Do you parse it as

(Every perceptual experience is such that)(it is possible that) it is delusory

or as

(It is possible that)(every perceptual experience is such that) it is delusory?

Do you think that one reading is correct (or at least the strongly preferred reading), and the other incorrect (or at least to be deprecated)? Or do you take (1) to be ambiguous between the ∀♢ reading (2) and the ♢∀ reading (3)?

Peter Geach in Reference and Generality takes it that (1) is unambiguously to be read as (3), with ‘every’ taking narrow scope. Or to be more accurate he talks — at p. 104 of the third edition —  about the fallacy in ‘the transition from “Any sense perception may be illusory” to “Every sense perception may be illusory”.’ I take it that the slight difference in wording is neither here nor there for the current point, and that the fallacy Geach is after is the fallacy of moving from ∀♢ to ♢∀. So indeed Geach is construing his  ‘every’ proposition as ♢∀ (and he doesn’t discern ambiguity).

Interestingly, however, when I asked [on Twitter] about (1), a couple of more-than-respectable voices in different necks of the logical woods agreed with Geach that (1) is not ambiguous — however, they claimed contra Geach that (1) is to be read as (2), i.e. ♢∀. Thus  “I don’t read [this] as ambiguous; [it] seems clearly to have the ∀♢ reading”. And “I can imagine situations where someone uses (1) to be ♢∀, but they’re all situations where someone is using [1] improperly or imprecisely”.

(B) Why is Geach so confident that in his ‘every’ proposition,  like in our (1), the quantifier has narrow scope, while in the corresponding ‘any’ proposition it has wide scope? For him, I think, this view goes with a more general view that ‘every’ takes narrow scope when ‘any’ takes wide scope. Thus contrast

If everyone loves Nerys, then Owen does,
If anyone loves Nerys, then Owen does.

Then, reasonably uncontroversially (and assuming no special emphasis on ‘anyone’), the normal readings of these propositions are different, and these will be regimented respectively as

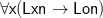
with ‘every’ having narrow scope with respect to the conditional, and vice versa for ‘any’. Indeed, I can imagine Geach armed with his scope principle saying “I can imagine situations where someone uses (1) to be ∀♢, but they’re all situations where someone is using (1) improperly or imprecisely”!!

(C) I take the disagreement between Geach and my twitter correspondents to be a bit of evidence in favour of my own view that both sides are wrong, and that — in the no-doubt corrupted state of modern chat! — (1) is pretty much ambiguous as it stands between the readings (2) and (3).

Now, actually, I don’t want or need to hang anything on this claim in the bit of my intro logic book which I’m re-writing. For when it comes to such quantified claims, it will be agreed on all sides that you do have to take note of questions of scope, even if you disagree about the verdicts. And that’s the crucial point you want when explaining that quantifiers, unlike proper names, have scopes.

Still, I’d be interested to know what other people’s linguistic intuitions are here!  Are you in the No Real Ambiguity camp about (1), and if so do you jump with Geach to the ∀♢ reading, or with some others to the ♢∀ reading? Are you in the You Can Read It Either Way camp? Do you have some other example of an ordinary language proposition mixing a quantifier and a modality which is, you think, a more compelling example of ambiguity? Do tell!

The post Every perceptual experience is possibly delusory appeared first on Logic Matters.

The stuff of nightmares

Once upon a time, John Corcoran and Stewart Shapiro reviewed a little book, by distinguished authors, from a distinguished press, What is Mathematical Logic edited by John N. Crossley for OUP. It’s the nightmare of getting to deserve a review like that which might rather slow a chap down as he tries to revise his own logic text …

The post The stuff of nightmares appeared first on Logic Matters.

The Pavel Haas Quartet play Shostakovich’s 2nd Quartet

The post The Pavel Haas Quartet play Shostakovich’s 2nd Quartet appeared first on Logic Matters.

Five books — Philosophy of Maths

You may very well know the Five Books website, where a wide-ranging cast of contributors are asked “to make book recommendations in their area of work and explain their choices in an interview”. The recommendations are often quirky, sometimes even slightly bizarre, but rarely without interest. It’s an illuminating and fun project.

There are a good number of topics in philosophy covered at Five Books, including some quite narrow ones. Though I am guessing that, reasonably enough, they are not going to get round to dealing with a topic of rather limited interest like the philosophy of mathematics. That thought sets me wondering: what five books in the area would I recommend in the same spirit as a Five Books posting. So here’s my selection — my selection today, at any rate: another day I might feel differently!

Modern philosophy of mathematics is still shaped by debates starting over a century ago, springing from the work of Frege and Russell, and also from Hilbert’s alternative response to the  “crisis in foundations”, and from the impact of Gödel’s work on the logicist and Hibertian programmes. All this is covered brilliantly and at relatively modest length in Marcus Giaquinto’s  The Search for Certainty: A Philosophical Account of Foundations of Mathematics (OUP, 2002) This is not just engaging and reliable but is written with very enviable clarity. (By all means, then go back to reading Frege’s Grundlagen, or dip into e.g. Bertrand Russell’s Introduction to Mathematical Philosophy. But you won’t find a better initial guide to those foundational debates than Giaquinto.)

Textbooks tend to present developed chunks of mathematics in a take-it-or-leave-it spirit, the current polished surface hiding away the earlier rough versions, the conceptual developments, the false starts. So Imre Lakatos’s Proofs and Refutations (originally 1963/4: CUP 1976) makes for a wonderful counterbalance. A classic exploration in dialogue form of the way that mathematical concepts are refined, and mathematical knowledge grows. We may wonder how far the morals that Lakatos draws can be generalised; but this remains a fascinating read.

The next book is a (too rare) example of a philosopher writing a mathematics book, engaging head-on with the conceptual issues the mathematics throws up. Michael Potter’s Set Theory and Its Philosophy (OUP 2004) is exactly what you need to read before trying to think about which brand of set theory (if any) to buy and why, or about the sense in which set theory is foundational, etc. The interplay between the mathematical and the philosophical here is very illuminating.

Many philosophers know a  bit about arithmetic and set theory: but there is a lot more to mathematics than that. If you want to engage philosophically with mathematics more widely, you need to have some sense of what is going on in some other areas of mathematics and to understand something of how these areas hang together (remember Sellars’s words about philosophy concerning itself with how things hang together …). I can’t think of a better place to start than with Saunders Mac Lane’s Mathematics: Form and Function (Springer 1986). You will need some, a little, mathematics to cope with this: but then you can’t hope to do the philosophy of X without knowing something about X! And this book is a remarkable achievement, written by a great mathematician with a genuine concern for some of the philosophical issues in the vicinity.

Thanks to the Stanford Encyclopedia and various series of Companions and Handbooks, it has never been easier to get up to speed with (fairly) recent work in various areas of philosophy. That’s certainly true in this area, thanks to Stewart Shapiro, ed., The Oxford Handbook of Philosophy of Mathematics and (Its) Logic (OUP 2005). Oddly the ‘its’ is missing from the book’s official title, but the essays here only talk about aspects of logic of concern to the philosophy of maths, and the ‘its’ is rightly there in the title of Shapiro’s own editor’s introduction. So here are 26 essays on aspects of the philosophy of mathematics and on relevant logical matters, written by a star cast, and — unlike many collections of this kind — at a pretty consistent level of accessibility and quality, and in some cases offering essays on opposing sides of major debates. Perhaps the overall coverage is slightly conservative in the choice of topics: but there is still a huge amount of interest here. If you don’t find a good proportion of these essays engaging and worthwhile, then mainstream philosophy of mathematics perhaps just isn’t for you.

So, with many regrets about what I’ve had to leave out, there are my suggestions for five books — I’d be very intrigued to hear yours!

The post Five books — Philosophy of Maths appeared first on Logic Matters.

Formal Theories of Truth

No one can say that Jc Beall, Michael Glanzberg and David Ripley have rattled on at self-indulgent length in their new OUP book Formal Theories of Truth. Just 119 small pages of main text. My kind of book, these days!

It’s elegantly organized, lively and engaging. First a general but carefully spelt-out version of a Liar Paradox derivation is set out. Then various options for escape are outlined. There’s a chapter on changing our inference rules for connectives, a chapter on restricting the inferences between P and T[P], a chapter on digging into the substructure of our logic, a short chapter on other directions to take. This is one very neat way of putting some order into the ramifying debates of formal treatments of the Liar. (It reads like an extended Stanford Encylopedia article — and indeed, that’s in effect what it is.)

The book is aimed, the authors say, at interested readers ‘with a little bit of formal logic training (even a first course in logic) who wish to take a first step into so-called formal theories of truth’. I wonder if those who have taken just a first logic course will fully ‘get’ e.g. the snappy claim that a diagonal lemma can be proved in the right settings (pp. 31-32) or will understand talk about limit ordinals (p. 44), etc. I’m not usually one to ask for a longer book. But I think this one, in fact, gives a bumpier ride than some of the ‘budding philosophers’ in the target audience will be comfortable with, and could sometimes have gone more slowly. Will the reader who hasn’t already been given an arm-waving lecture explanation really pick up, e.g., the beautiful idea underlying Kripke’s theory?

Still, for readers who are perhaps a little past the budding stage, who have perhaps had some first fleeting encounters with a formal theory of truth or two, and are in need of a way of organizing and interrelating the fragments they know about, in order to get into a good position to move on to tackle more details, this can be warmly recommended as exactly the book they have been wanting.

The post Formal Theories of Truth appeared first on Logic Matters.

One that got away

We were looking the other evening for our copy of a lovely book, Nathan Silver’s 1968  Lost New York. I remember buying it second hand when we had no money, perhaps five years after it was first published, in the even-then old-fashioned warren that was Galloway and Morgan in Aberystwyth. The book is a  photographic essay on the lost buildings and streets of a past city. It is very evocative, not that I’ve ever been to New York, or now ever will (but then the city of the mind —  of Edith Wharton, say — is not there to be visited). But there’s something about glimpses of cities the day-before-yesterday, though I find it hard to put into words the deep appeal I find in them.

We couldn’t believe it that the book had gone. Somehow, in a mad moment, in one of those necessary fits of clearing out to keep at bay the ever over-flowing shelves, we must have looked at each other and said ‘have you looked at that in a dozen years or more? no?? then it should go to Oxfam!’. But we can’t remember how we ever came to agree that. For the book is a delight to browse in occasionally, and we were sentimentally attached to it. How odd.

So I have found a copy online, absurdly cheap. And here it is again. But not quite as we remember it — for this is a later reprint, and at least in our memory the original photographic reproductions were sharper, on glossier paper. But maybe our memories play us false, and it’s just that a replica isn’t quite the original with its own small history.

The post One that got away appeared first on Logic Matters.

Button & Walsh: Philosophy and Model Theory

It is always pleasing to be able to warmly recommend a new book. So let me enthusiastically draw your attention to this newly published book by Tim Button and Sean Walsh, Philosophy and Model Theory, just published by OUP. (The pbk is £30 — but this is xvi + 517 larger-format and action-packed pages, so we certainly can’t complain!)

This is a unique book, both explaining technical results in model theory (eventually at a pretty non-trivial level), and exploring the appeals to model theory in various branches of philosophy, particularly philosophy of mathematics, but in metaphysics more generally (recall ‘Putnam’s model-theoretic argument’), the philosophy of science, philosophical logic and more. So that’s a very scattered literature that is being expounded, brought together, examined, inter-related, criticised and discussed. Button and  Walsh don’t pretend to be giving the last word on the many and varied topics they discuss; but they are offering us a very generous helping of first words and second thoughts. It’s a large book because it is to a significant extent self-contained: model-theoretic notions get defined as needed, and many of the most philosophically significant results are proved.

The book only arrived yesterday, so at this point I have to report just having read the opening four chapters (two carefully, two more quickly) and dipped very speedily in and out later in the book. But it seems to me that — in fact, as you’d expect from these authors — the expositions of the techie stuff is quite exemplary (they have a good policy of shuffling some extended proofs into chapter appendices), and the philosophical discussion is done with vigour and a rather engaging style. The breadth and depth of knowledge brought to the enterprise seems to be remarkable.

So first impressions: this book looks as if it is an outstanding achievement. Logic-minded philosophers should find it fascinating; and — with judicious skimming/skimming (the signposting in the book is excellent) — so should mathematicians with an interest in some foundational questions. Make sure it is in your university library (and at that price, in your library!).

The post Button & Walsh: Philosophy and Model Theory appeared first on Logic Matters.

On Frege seeing what is in front of his nose

Take a mathematician of Frege’s generation, accustomed to writing the likes

(1)

(2) If , then or ,

— and fancier things, of course!

Whatever unclear thoughts about ‘variables’ people may or may not have had once upon a time, they have surely been dispelled well before the 1870s, if not by Balzano’s 1817 Rein analytischer Beweis (though perhaps that was not widely enough read?), at least by Cauchy’s 1821 Cours d’analyse which everyone serious will have read. Both Bolzano and Cauchy take claims like (1) and (2) to be true just if each instance is true, plain and simple, and clearly gloss various claims written with variables as claims holding ‘for any value of x’. Maybe it is worth noting, then, that the mathematicians of the day, at least when on their best behaviour, could be very decently clear about this!

But then it seems to be only the tiniest of steps to say outright that an ideal notation for such claims might have the form ‘for any value of , 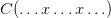’, and that such an explicit form is true when ‘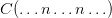’ is true whatever ‘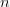’ names. So — looked at from this angle — the wonder is not that Frege came up with his basic account of the logical form of expressions of mathematical generality like (1) and (2), but that no one had quite said as much before.

If you go back to Bolzano’s 1810 Beyträge, what happens there (with hindsight) seems very odd indeed. After all, here is someone who within a few years — in his 1816 Der binomische Lehrsatz and (even more) the 1817 Rein analytischer Beweis — is very clear indeed about variables and their use, when making essential practical use of quantification in talking about continuity etc. Yet in the earlier Beyträge, his Contributions to a Better-Grounded Presentation of Mathematics, when Bolzano turns to talking about logic and the principles of deduction, he looks quite antediluvian — and as far as I know he never revisited the logical basics to try to do better. OK, he says the mathematician will need more principles than we’ll find in the traditional syllogistic, and your hopes rise just for a moment: but the additional principles he comes up with are such a very limited and disappointing lot — the likes of A is an M, A is an N, so A is an M-and-N. It seems that the Bolzano of the Beyträge is — despite his disagreements and amendments — so thoroughly soaked in Kant and in broadly Aristotlean logic that he just can’t see what is right in front of his nose in the mathematician’s use of variables.

At least here, then, Frege’s originality — it might be said — is not depth of insight but his unabashed willingness to take the mathematician’s usage of the likes of (1) and (2) at bald face value, and to not try to shoehorn such generalizations into the canonical forms sanctioned by received wisdom. It is as if his now standard treatment of generality is a very happy result of Frege’s knowing rather little of previous logic and philosophy.

I have often wondered, then, if Frege’s philosophical commentators have seen his basic discovery of a quantifier(-for-scoping)/variable notation as more exotic than it is. Take the pre-Frege usage of mathematician’s variables-of-generality at face value, without preconceptions (“don’t think, look” as Wittgenstein might say). Then note that we must distinguish generalizing a negation (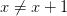) and negating a generalization (it’s not true in general that ) — so if we are going to use a symbol for negation we are going to somehow have to mark relative scopes. And we are already more or less there!

Now, in Begriffsschrift and pieces written around that time, Frege’s concern seems to be very much with regimenting mathematical language (formalizing the logical bits of it to go along with the common formal expressions we use for the non-logical bits, showing how adding the logical bits allows us to neatly cut down on the non-logical primitives by giving us the resources to define more complex concepts out of simpler ones, etc. etc.). He says remarkably little — except in using a few toy examples like the ‘Cato killed Cato’ one — about ordinary, non-mathematical, language more generally. So e.g. Dummett’s reading of Frege from the very beginning as aiming for a story about the real underlying structure of ordinary language generalizations is arguably considerable over-interpretation: Frege seems at least in Begriffsschrift to be more in the business of giving us a tidied up replacement for informal ways of talking, useful in regimenting science — one modelled, to borrow his phrase, upon the formula language of arithmetic.

Saying all this is of course not for a moment to underplay the depth of Frege’s reflections consequent on his discovery of the quantifier/variable notation! But I would very much like to know if there are any discussions in the history of maths or history of logic literatures on the how variables were regarded in 19th century mathematics.

The post On Frege seeing what is in front of his nose appeared first on Logic Matters.

Names and quantifiers

‘Socrates is a philosopher’ gets rendered into an appropriate formal language of predicate logic by the likes of 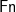; ‘Someone is a philosopher’ gets rendered by 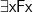. The syntactic difference between a formal name and a quantifier-tied-to-a-variable vividly marks a semantic difference between the rules for interpreting the two resulting formal wffs. And there isn’t the same sort of immediately striking syntactic difference between the vernacular name ‘Socrates’ and the quantifier ‘someone’.

That’s agreed on all sides, I guess. But many have wanted to say more — namely that, in English, there is no syntactic difference between the name and the quantifier. Thus,

Quine writes that ‘one of the misleading things about ordinary language is that the word “something” masquerades as a proper name’. Well, presumably there is no masquerade if you can easily tell them apart by their surface look. So, more carefully, Quine’s idea is presumably that the English quantifier is just like a proper name as far as surface sentence structure is concerned. Or as Michael Dummett explicitly puts it: ‘As far as the sentence-structure of natural language is concerned, signs of generality such as “someone” and “anyone” behave exactly like proper names — they occupy the same positions in sentences and are governed by the same grammatical rules.’

But this is just not true (as Alex Oliver, for one, has had fun pointing out). Thus, contrast ‘Something wicked this way comes’ with the ungrammatical ‘Jack wicked this way comes’, or ‘Someone brave rescued the dog’ with ‘Jill brave rescued the dog’. Or contrast ‘Foolish Donald tweeted’ with the ungrammatical ‘Foolish someone tweeted’. Compare too ‘Senator, you’re no Jack Kennedy’ with ‘Senator, you’re no someone’. Or what about ‘Hey, Siri!’ compared with ‘Hey, someone!’?

Other quantifiers too aren’t interchangeable with names. Consider ‘Nobody’. We get similar failures of substitution: we can’t replace ‘Nobody wise …’ with ‘Jill wise …’, or replace ‘Foolish Donald …’ with ‘Foolish nobody …’, and preserve grammaticality, etc. And ‘Nobody ever finishes War and Peace’ constrasts with the ungrammatical ‘Jack ever finishes War and Peace’, while ‘Jill never finished War and Peace’ contrasts with ungrammatical ‘Nobody never finished War and Peace’.

And so it goes. Quine’s and Dummett’s claims simply overshoot. English grammar doesn’t treat names and quantifiers exactly on a par. But even if it did, ordinary language would only be “misleading” (in Quine’s word) if there was some tendency for us ordinary speakers to get misled. Now, Mark Sainsbury indeed talks of ‘our tendency to regard quantifiers … as names’. But what is the evidence is that we have such a tendency? This is shown, says Sainsbury, ‘by the fact that Lewis Carroll’s jokes are funny’. But that really is hopeless! After all, Carroll’s wordplay (you know the kind of thing: ‘I see nobody on the road,’ said Alice. ‘I only wish I had such eyes … To be able to see Nobody!’ etc. etc.), apart from being wearyingly unfunny, has nothing specifically to do with confusing quantifiers with names (as Alex Oliver notes, it’s pretty much on a par with the likes of ‘What’s your name?’ ‘Watt.’ ‘I said, what’s your name?’ ‘Watt’s my name’ …)

OK: Quine, Dummett are wrong that English names and quantifiers “are governed by the same grammatical rules”, and even if they weren’t, that would give us no reason to suppose that we are misled (Quine, Sainsbury) by the grammatical similarity or that we tend to regard quantifiers as names.

And yet, and yet … Even if the claim that “signs of generality behave exactly like proper names” is false au pied de la lettre, we are left with the feeling that the sort of exceptions we’ve noted are somehow quirks of idiom rather than deeply significant. We are left with the sense that there is something important and true which ought to be  rescuable from the very familiar kind of remarks from Quine Dummett and Sainsbury. But what is it? We say arm-waving things in our intro logic lectures — but what will we happy to put in black and white?

It is tempting to say this:  the syntax of our formal first order language more perspicuously tracks the semantics of the formal language than the syntax of English names vs quantifiers tracks their semantics. But in a way, this is just too easy to say. Of course  the syntax tracks the semantics in our formal language in a way that is  perspicuous even to beginners — we purpose-designed the language to be exactly that way! And who knows how things are in English when it comes to syntactic or semantic theory — of course that’s not perspicuous at all, as half a century of modern linguistic theory has shown?!

Now, Quine, Dummett and Sainsbury aren’t  aiming to contrast the known with the unknown: they make a positive (even if false) claims about English, after all. But then, to repeat the question, just what that is instructive and importantly true can we extract from those incorrect claims about quantifiers “behaving exactly like” (?!) names in English but not in first order languages? I have (or rather had) my lecture patter. But, as I think about the relevant bit of my revised IFL book, I’d be very interested to know what others say to their students!

The post appeared first on Logic Matters.