Peter Smith's Blog, page 58
May 1, 2020
Boris Giltburg plays Beethoven’s Pathétique
As well as streaming lunchtime performances from his home (see his Facebook page), Boris Giltburg is still occasionally releasing filmed performances from his ongoing project to play all 32 sonatas in Beethoven’s 250th anniversary year. The latest is this terrific performance of the Pathétique, the 8th sonata. The previous seven, along with Giltburg’s always interesting introductory descriptions, can be found here. This is such life-affirming playing for these troubled times.
The post Boris Giltburg plays Beethoven’s Pathétique appeared first on Logic Matters.
April 30, 2020
Luca Incurvati’s Conceptions of Set, 9
Naive set theory entails contradictions. Really bad news. Or so most of us think. But what if we are prepared to be more tolerant of contradictions, e.g. by adopting a dialethic and paraconsistent logic, which allows there to be contradictions which are true (as well as false) and where contradictions don’t entail everything? Could we rescue the naive conception of set, accommodate e.g. the idea of a Russell set, by departing from classical logic in this way? A desperate measure, most of us will think. Even if willing, once upon a time, to pause to be amused by varieties of dialethic logic, at this late stage in the game, I don’t have much patience left for the idea of going naive about sets by going far-too-clever-by-half about logic. But Luca is evidently a lot more patient that I am! He devotes Chapter 4 of his book to investigating various suggestions about how to save naive set theory by revising our logic. How does the story go?
Luca very helpfully divides his discussion into three main parts, corresponding to three dialethic strategies.
The first he labels the The Material Strategy — we adopt a non-classical logic which keeps the material conditional, so that  is still simply equivalent to
is still simply equivalent to 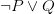 , while we reject the classically valid disjunctive syllogism, and hence material modus ponens.
, while we reject the classically valid disjunctive syllogism, and hence material modus ponens.
Graham Priest initially thought that a ‘simple and natural choice’ here is his LP, the Logic of Paradox. But LP doesn’t validate the transitivity of the material conditional, and this hobbles the proof of various elementary theorems of set theory — even the usual proof of Cantor’s Theorem fails. And on the usual definition of set identity in terms of coextensionality, Leibniz’s Law fails too.
Can we tinker with LP to avoid these troubles? Luca mentions a few options: all of them have equally unattractive features — giving us a set theory that is too weak to be useful. So, Luca’s verdict seems right: the prospects of saving naive set theory as a formal theory by developing the material strategy in anything like the way originally suggested by Priest are dim indeed.
What about the second strategy The Relevant Strategy, where we adopt a relevant logic that does validate modus ponens? Luca dives into an extended discussion of so-called depth-relevant logics, also advocated by Priest. We won’t follow the ins and out of the arguments here. But it is again hard not to agree with Luca’s eventual verdict that (i) “Priest does not seem to have offered a good argument for focusing on the logic he is considering,” and further (ii) the logic is in any case still too weak for us to carry out standard arguments in set theory. At which point, most of us would get off this particular bus! But Luca takes us on another couple of stops, considering some proposals from Zach Weber for strengthening the depth-relevant logic. The argument become more involved, but again Luca arrives at a strongly negative verdict (enthusiasts can follow up the details): Weber’s logic remains poorly motivated — I would say it smacks of ad-hoc-ery — and Weber’s resulting theory lacks a genuine principle of extensionality so in the end can’t be regarded as a set theory anyway.
That leaves us with a third strategy also to be found in Priest, The Model-Theoretic Strategy. An intuitionist can allow that classical logic is just fine when we are reasoning about decidable matters. Similarly, the idea now is, that a dialetheist can allow that classical logic is just fine when we are reasoning over consistent domains. So the dialetheist can continue to reason classically about a consistent core subdomain of sets — e.g. the cumulative hierarchy — while asserting that this is just part of the full universe of naive set theory, about which we must reason dialethically.
There is, you might well think, an immediate problem about this position. If you accept the cumulative hierarchy as a consistent core universe of sets about which we can argue classically, and which gives us all the sets we can want for mathematical purposes (ok, push the hierarchy up high enough to keep the category theorists happy!), then just what are we getting by adding by more putative sets, the inconsistent ones? It’s not like adding points at infinity to the Euclidean plane, for example, to give us an interestingly enriched mathematical structure (results about which can be reflected down into interesting new results in the original domain). And I’m ‘naturalist’ enough in Maddy’s sense to ask: if the putative enriched structure of naive set theory isn’t mathematically interesting, why bother?
But I’ve jumped the gun: what does this supposed enriched structure look like? With some trickery which Luca describes, we can explain how to extend a model of ZF to become a model of a naive set theory with LP as its logic (so the formal theory might be inadequate to work inside, as argued before, but still have a rich model). But why suppose that this particular fancied-up model captures the structure of the full supposed universe of a naive set theory? As Luca points out, we have no good reason to suppose that. But then “the paraconsistent set theorist needs, after all, to say more about what the universe of sets looks like. It is not enough to simply suppose that it contains some paradigmatic inconsistent sets and has the cumulative hierarchy as an inner model.” The story is radically incomplete.
Summing up, the idea of rescuing naive set theory by going dialethic, using any of the three strategies, looks to be degenerating research programme. Probably many of us would have predicted that outcome! — but we can thank Luca for doing the hard work of confirming this in some detail.
And that takes us to the end of Chapter 4, and a bit more than half way through the book. And for most readers, the three remaining chapters promise to be considerably more interesting than the one we’ve just been looking. Next up, for example, is a discussion of the commonly-encountered idea of `Limitation of Size’.
The post Luca Incurvati’s Conceptions of Set, 9 appeared first on Logic Matters.
April 28, 2020
Luca Incurvati’s Conceptions of Set, 8
We have reached the last few pages of §3.6; we are still considering whether the iterative conception delivers Replacement. Luca has critically considered two proposed routes from the one to the other; he now turns to discuss a third, an Argument from Reflection.
Naively put, reflection principles tell us that, for any property — or at least, any kosher property of the right kind! — belonging to the universe of all sets, we can find a level of the hierarchy which already has that property. In other words, kosher properties of the whole universe are “reflected” down to a set-sized sub-universe. Three interrelated questions arise:
Does the iterative conception sanction any form of reflection principle like this, and if so why?
How are we to spell out, more formally, some acceptable form(s) of reflection principle? What are the kosher properties that can get reflected down?
Which formal reflection principles entail Replacement?
On (1), Luca outlines a supposed link between (i) the idea that iteration goes on ‘as far as possible’ with the idea (ii) that the hierarchy should be ‘absolutely infinite’ in the sense that it resists unique characterization by any non-trivial property. And from (ii) it is supposed to follow that any property we can correctly assign to the universe must fail to pin down the full universe, so (iii) that property will already exemplified by some initial part of the hierarchy.
But I don’t really get the supposed link between (i) and (ii). At the end of his discussion, Luca claims that “absolute infinity is a natural way of understanding the idea that the iteration process is to be carried out as far as possible.” But I could have done with rather more explanation of why it should seem natural. And indeed I could have done with a more about the step from (ii) to (iii).
But ok, let’s grant that for some class of kosher properties, there is an intuitively appealing chain of reasoning that leads naturally enough from the iterative conception to reflection for those properties.
We now need to go formal: how do we formally capture the relevant reflection principles? The discussion of (2) and (3) inevitably becomes more technical. I won’t attempt to summarize here Luca’s already rather compressed exploration (which also touches on closure principles as a weaker alternative to reflection principles). In fact, I suspect many readers of the book will find this episode pretty tough going. Those beginners who needed e.g. to be reminded about cardinals and ordinals at the end of Chapter 1 are surely not going to easily follow this discussion which turns, inter alia, on distinguishing which order of higher-order variables are allowed to occur parametrically in formal versions of reflection principles. But yes, a strong enough formal reflection principle will entail Replacement. Still, I suppose someone might well pause to wonder whether the required open expressions with higher order parameters express kosher properties of the kind that were being countenanced in the intuitive considrations at stage (1).
Overall, I found Luca’s discussion of what he calls the Argument for Reflection intriguing (it got me re-reading some of the literature he mentions), but inconclusive. But then he too in the end is cautious. He says that “if the idea of iteration as far as possible is perhaps not part of the iterative conception, it harmonizes well with it. Understood or augmented in this way, the iterative conception sanctions the Axiom of Ordinals and possibly the Replacement Schema”. [my emphasis]
Which gets us to the end of Chapter 3, responding to some initial ‘Challenges to the Iterative Conception’. So let’s pause here. The rest of the book looks at various rivals to the iterative conception, starting in Chapter 4 with the naïve conception again — can we, after all, rescue it from its apparently damning inconsistency by departing from classical logic? I’ll discuss the whole chapter in one bite in the next posting!
The post Luca Incurvati’s Conceptions of Set, 8 appeared first on Logic Matters.
April 27, 2020
From a small corner of Cambridge, 5

The days are often very long, yet the weeks seem to fly by. Such odd distortions of time as we are knocked out of our usual patterns of life.
We have been walking out on Midsummer Common most days, in wonderful weather, with almost no-one else around, just the occasional runner or dog-walker whom you can easily dodge. But gone for now are our old regular habits of dropping into one or another of a couple of coffee shops on the far side of the Common. It is such little things that you miss. We took a decision years ago not to have a serious coffee machine at home, partly because there’s little space on the kitchen worktops, but mainly to encourage us to leave the house and have a decent walk in order to have proper espressos and to get some friendly human contact too. Who knows when that can all begin again?
It was my birthday a couple of weeks ago. Once upon a time in olden days, BC, we’d thought of going up to London to visit the Artemisia exhibition at the National Gallery. Well, that didn’t happen, either the exhibition or the visit. But as a present I did get the catalogue which has been published and is terrific. In fact, aren’t many art exhibition catalogues these days just wonderful? Quite beautifully produced, with often very readable and illuminating essays (which, judging by the characteristic pages of endnotes, are grounded in a huge amount of scholarship lightly worn), and all for the price of a couple of exhibition entry tickets. This book is no exception. We saw the Artemisia exhibition in Rome a few years ago; and yes of course it is a great pity not to experience again the visual impact of some of those dramatic canvasses face to face (and that seems the appropriate description). But this catalogue is much more than a small consolation: it’s an art-work in itself and very enjoyable. So that’s this week’s lockdown book recommendation!
But as a present I did get the catalogue which has been published and is terrific. In fact, aren’t many art exhibition catalogues these days just wonderful? Quite beautifully produced, with often very readable and illuminating essays (which, judging by the characteristic pages of endnotes, are grounded in a huge amount of scholarship lightly worn), and all for the price of a couple of exhibition entry tickets. This book is no exception. We saw the Artemisia exhibition in Rome a few years ago; and yes of course it is a great pity not to experience again the visual impact of some of those dramatic canvasses face to face (and that seems the appropriate description). But this catalogue is much more than a small consolation: it’s an art-work in itself and very enjoyable. So that’s this week’s lockdown book recommendation!
The post From a small corner of Cambridge, 5 appeared first on Logic Matters.
April 25, 2020
Luca Incurvati’s Conceptions of Set, 7
In a couple of very well known papers, George Boolos argued that “the axioms of replacement do not follow from the iterative conception”. Was he right? Or can Replacement be justified on (some core version of) the iterative conception? This is the topic of the particularly interesting §3.6 (pp. 90–100) of Conceptions of Set, ‘The Status of Replacement’.
Luca discusses three lines of argument to be found in the literature for the thought that the iterative conception does warrant Replacement. I’ll comment on two in this post.
The first he calls Gödel’s Argument. Two quotes from Gödel: (i) “From the very idea of the iterative concept of set it follows that if an ordinal number α has been obtained, the operation of power set P iterated α times leads to a set Pα(∅)” And then (ii) “the next step will be to require that any operation producing sets out of sets can be iterated up to any ordinal number.”
In response, Luca makes the following central points:
Tait and Koellner have argued that elaborating Gödel’s claim (i) requires appeal to Choice. But not so. For we can work with the Scott-Tarski definition of an ordinal, and then, without needing an assumption of Choice, Gödel’s thought will at least warrant adding to Z+ the Axiom of Ordinals — the axiom that there is a level Vα for every ordinal α.
This theory with the Axiom of Ordinals is rich, much more powerful than Z+, and in fact buys us the nice results that Boolos claimed for Replacement. However, the Axiom of Ordinals is weaker than full Replacement.
A version of Gödel’s second claim (ii) is needed to get us from the iterative conception to full Replacement, and it isn’t clear why (ii) should be thought of as part of the iterative conception.
On (1), accepting Gödel’s (i), Luca’s discussion seems spot on. On (2) quite a few readers (those familiar with ZFC but who haven’t read Potter’s book) might well have welcomed rather more at this point on the Axiom of Ordinals, on its virtues and mathematical consequences. They might reasonably ask: if the Axiom of Ordinals in fact gives us (a good deal of) what we want, just why — other than conservative adherence to tradition! — should we buy full-power Replacement? On (3), we could I suppose go back to pause over (i) to wonder if the idea of the universe of sets being layered by iterating the set of operation has to go along with the idea that those iterations should be ordinal-many (for any ordinal we can obtain). But leave that aside: Luca it is surely right that it is one thing to build into the iterative conception the idea that the core set of operation should in some sense be iterated ‘as far as possible’, it is another thing to require that other operations be iterated as far as possible too.
The second line of argument for Replacement to be discussed is what Luca calls The Argument from Co-finality. Thinking in terms of stages of the hierarchy, Shoenfield (in his famous Handbook article) suggests that for any collection of stages S, there will be one after it “provided that we can imagine a situation in which all of the stages in S have been completed”. But then assume that we have a set x and for every y in x there is a stage Sy correlated somehow or other with y. Then
Suppose … we take each y in x … and complete the stage Sy. When we reach the stage at which x is formed, we will have formed each y in x and hence completed each stage Sy.
So if S is the collection of stages Sy, we can imagine a situation in which all of the stages in S have been completed and there will be a stage after it.
Now, if we buy this cofinality principle, then Replacement is immediate (since Replacement tells us that the image of x under a function f will itself be a set; for each y in x take Sy to be the stage at which f(y) is formed, and then by Shoenfield’s principle there will be a stage after all those at which we can gather together all the f(y) into a set …).
What are we to make of all this? Luca surely hits the nail on the head! As he neatly notes, Shoenfield’s argument
seems to assume that if a process can be completed, and we replace each stage of the process with a process that can be completed, then the maxi-process consisting of all these processes can itself be completed. But this is just the Axiom of Replacement reformulated in terms of stages and processes.
The supposed defence of Replacement is therefore too close to being circular.
So we haven’t got here an independent argument from the iterative conception to Replacement. Luca concludes, however, on a (surprisingly?) sympathetic note: “the cofinality principle certainly seems to harmonize well with the iterative conception, and can perhaps be seen as one way of spelling out the idea that the cumulative process through which the hierarchy is obtained should be iterated as far as possible.” But equally couldn’t we spin it the other way? — the iterative conception itself doesn’t take us as far as Replacement, and it takes a further independent thought to justify that principle. Which leaves us with the question of what rival further thoughts (equally harmonizing with the basic iterative conception) might be on the cards.
To be continued on a third line of argument for Replacement, via reflection principles.
The post Luca Incurvati’s Conceptions of Set, 7 appeared first on Logic Matters.
April 22, 2020
Book note: Ralf Krömer’s Tool and Object
It is inevitably going to be difficult to write illuminatingly about the history of category theory. For this is entangled with the distinctly complicated history of mid-twentieth-century topology. Colin McLarty sees the difficulty like this:
For even a rough understanding of [just some of] the problems [topologists] faced we would have to go into the array of homology theories at the time and the forefront of 1940s abstract algebra, and we would do this without using category theory, and we would waste a lot of time on things category theory has now made much easier. We could give a few trivial examples just before reversing the order of discovery to define categories, functors, and natural transformations but precisely the examples serious enough to have motivated the definitions are too hard to be worth giving now without benefit of categorical hindsight.
Is that too pessimistic? Well, this much is surely true. It would take rather exceptional expositional skills, combined with an exceptional depth of mathematical understanding, to be able to helpfully isolate and explore critical moments in the development of category theory, while doing this in a way that is both detailed and yet also still quite widely accessible.
For different reasons, it is a challenge too to write illuminatingly about the philosophy of category theory. Working out what is really novel about categorical concepts and approaches isn’t easy. Working out in what senses category theory does or does not provide a new kind of foundation for mathematics isn’t easy. And we are not exactly helped by the fact that some category theorists are wont to make distractingly sweeping claims about the philosophical significance of what they are up to, claims which are hard to deconstruct. So it would take a different set of skills, beginning with a serious feel for the philosophy of mathematics more generally, to tackle the philosophy of category theory.
 It is highly ambitious of anyone, then, to take on writing a book which is intended to be both ‘A History and Philosophy of Category Theory’. But that’s the subtitle of Ralf Krömer’s 2007 book Tool and Object. This has been on my ‘must read one day’ list for quite a while. I’ve at last had time to take a serious look at it. How well does Krömer succeed at the daunting dual task?
It is highly ambitious of anyone, then, to take on writing a book which is intended to be both ‘A History and Philosophy of Category Theory’. But that’s the subtitle of Ralf Krömer’s 2007 book Tool and Object. This has been on my ‘must read one day’ list for quite a while. I’ve at last had time to take a serious look at it. How well does Krömer succeed at the daunting dual task?
I found the book a very considerable disappointment, even allowing for the difficulties we’ve just mentioned. Life being short and all that, I’ve decided against a chapter-by-chapter commentary here, as it would take a lot more time than it would be worth, either for me as writer or for you as reader. But in headline terms, the philosophical bits are just far too arm-waving for someone of my analytic tastes; and I found the historical mathematical exposition just too unhelpful, even for someone coming to the party with a decent amount of mathematical background. The exception, perhaps, is Chapter 6, ‘Categories as sets: problems and solutions’ which is more closely focused on one familar issue, and is quite a useful guide to some of the discussions on “The possibilities and problems attendant on the construction of a set-theoretical foundation for CT and the relevance of such foundations”. And forgive me if I leave it at that. Your mileage may vary of course; but I can’t recommend this book.
The post Book note: Ralf Krömer’s Tool and Object appeared first on Logic Matters.
April 21, 2020
Luca Incurvati’s Conceptions of Set, 6
In §3.3 of Conceptions of Set, Luca discusses what he calls the ‘no semantics’ objection to the iterative conception. He sums up the supposed objection like this:
Consider the case of iterative set theory, which for present purposes will be our base theory Z+. Since the set-theoretic quantifier is standardly taken as ranging over all sets, it seems that one of the interpretations quantified over in the definition of logical validity for L [the standard first-order language of set theory] – the intended interpretation – will have the set of all sets as its domain. But there can be no set of all sets in Z+, on pain of contradiction. Hence, the objection goes, if we take all sets to be those in the hierarchy, we cannot give the usual model-theoretic definition of logical validity.
Or rather, that is how the objection starts. Of course, the further thought that is supposed to give the consideration bite is that, if we can’t apply the usual model-theoretic definition of logical validity, then we are bereft of a story to tell about why we can rely on the inferences we make in our set theory when we quantify over all sets.
As Luca immediately remarks, this challenge is not especially aimed at the iterative conception: any conception of the universe of sets that rules out there being a set of all sets will be open to the same prima facie objection. It looks too good to be true!
Graham Priest is mentioned as a recent proponent of this objection. But as Luca point out, Kreisel over fifty years ago both mentions the issue raised in the quote and has a response to what I called the further thought which is supposed to make the issue a problem. For Kreisel’s ‘squeezing argument’ is designed precisely to show that we have a perfectly good warrant for using standard first-order logic as truth-preserving over all structures, not just the ones that can be formally regimented in the usual model-theoretic way. I’ve defended Kreisel’s argument, properly interpreted, e.g. here: so I’m more than happy to go along with Luca’s endorsement.
Luca does, however, have other things to say about the ‘no semantics’ objection before turning to Kreisel’s way out. As he notes, we can hold onto the idea that we can sensibly quantify over all sets, and hold on to the core of the classical Tarskian definition of validity, by denying that domains have to be taken to be sets. Of course, there is little point in arm-wavingly talking about classes instead of sets as if that by itself resolves anything. What we need to do is to reject what Richard Cartwright calls the All-in-One Principle which tells us that to quantify over some things presupposes that there’s a set (or proper class, or other single object-in-its-own-right) to which they all belong. We can speak, if you like, of virtual classes, classes-as-many, i.e. we can use a singular idiom for talking about objects, plural. But better, we should just go straight to giving the semantics for FOL in a plural metalanguage, saying that quantifiers range over objects (one or many), interpretations assign e.g. monadic predicates some of these objects (zero, one or many), and so on. We know this can be done, and the plural metalanguage itself formalized — Oliver and Smiley show how do this in all the detail you could want in their Plural Logic. I’m really not sure why Luca doesn’t mention the possibility of taking the plural route here, as it would surely give him another rebuttal of the further thought that drives the `no semantics’ objection.
What Luca does discuss is another way of giving up the idea that the domain of quantification is an object which he finds in work by Rayo, Williamson and Uzquiano. They propose a higher-order semantics where our metatheory is to be regimented in a second-order way. I don’t find this especially natural, and it is not at all clear to me why going higher-order should be thought a better bet than staying first-order but allowing plurals.
The post Luca Incurvati’s Conceptions of Set, 6 appeared first on Logic Matters.
April 19, 2020
Choice and ignorance
I was very struck by the following remark made in passing on Asaf Karagila’s blog:

We know absolutely nothing … I’m always pulled up short when reminded about gaps in our knowledge like this! Why are these things so hard?
The post Choice and ignorance appeared first on Logic Matters.
April 18, 2020
Lockdown listening: online opera etc.
I was late to notice that the terrific Bachtrack site is keeping a very well organized list of online streaming opera, dance, concerts, etc. So just in case you too had missed it, here’s a link. The Guardian also has an excellent and frequently updated guide to Lockdown Listening.
The post Lockdown listening: online opera etc. appeared first on Logic Matters.
Bachtrack’s guide to online opera etc.
I was late to notice that the terrific Bachtrack site is keeping a very well organized list of online streaming opera, dance, concerts, etc. So just in case you too had missed it, here’s a link.
The post Bachtrack’s guide to online opera etc. appeared first on Logic Matters.



