Peter Smith's Blog, page 57

Luca Incurvati’s Conceptions of Set, 13

Among other things, I need to get more answers to the exercises in IFL2 online before publication, and that’s a ridiculously time-consuming task, which is no doubt why I’ve been rather putting it off! Doing some of the needed work partly explains the hiatus in getting back to Luca’s book. But there’s another reason for the delay too. I’ve found it quite difficult to arrive at a clear view of the second half of his Chapter 6 on NF. However, I must move on, so these remarks will remain tentative:

Early on, in §1.8, Luca distinguished what he called logical and combinatorial conceptions of set. And now in §6.7, he tells us that NF can be treated as a theory of logical collections.

It is a familiar claim that some such distinction between logical and combinatorial collections is to be made. And it seems tolerably clear at least how to make a start on elaborating a combinatorial conception: the initial idea is that, take any objects, however assorted and however arbitrarily selected they might be, they can be combined to form a set with just those objects as members. And then it is reasonable to argue that the iterative conception of set is a natural development of this idea. It is much less clear, however, even how to make a start on elaborating the so-called logical conception. Let’s pause over this again before turning to the details of §6.7.

In §1.8, Luca suggests “Membership in a logical collection is determined by the satisfaction of the relevant condition, falling under the relevant concept or having the relevant property. Membership is, in a sense, derivative: we can say that an object a is a member of a [logical] collection b just in case b is the extension of some predicate, concept, or property that applies to a.” But are there going to be enough actual predicates (linguistic items) to go around to give us the sets we want? Which language supplies the predicates? If we say ‘a logical set is the extension of a possible predicate’ then we are owed an account of possible predicates — and in any case, this doesn’t really seem to tally with the idea of membership as a derivate notion: the picture now would rather seem to be that here already are the sets with their members, and they are (as it were) waiting to be available to serve as extensions for any predicates that we might care to cook up in this or that possible language.

So maybe we need to concentrate on the concepts or properties? The notion of a concept here is slippery to say the least, so let’s think about properties for a bit. How plentiful are properties? We don’t want to get too bogged down in metaphysical discussions here, but for orientation let’s recall that David Lewis famously makes a distinction between the sparse natural ‘elite’ properties (which can appear in laws, where sharing such a property makes for real resemblance, etc., etc.) and the abundant non-natural properties (where Lewis explicitly explains that for any combinatorial set of actual and possible objects, however gerrymandered, there is an abundant property, namely the property an object has just in case it is a member of the given set). Now, taking logical sets to be the extensions of properties in an abundant sense which is anything like Lewis’s will just collapse the supposed logical/combinatorial distinction.

But on the other hand, taking logical sets to be always the extensions of properties in some narrower sense would again seem to be in danger of giving us too few sets. It is a common argument, for example, that x’s being, as we might casually say, F or G is really just a matter of x’s being F or x’s being G — the world doesn’t contain, as part of its furniture, as well as the property F and the property G the disjunctive property F-or-G. In other words, even if F and G are real properties which have logical sets as extensions, there is no real property F-or-G to have the union of those sets as its extension. Drat! So perhaps we do want to be thinking in terms of predicates after all, since we can apply Boolean operations of predicates (and get unions and intersections of extensions) in a way we can’t apply them to natural properties (at least on some popular and well-defended views). But defining sets in terms of predicates wasn’t looking a great idea …

The nagging suspicion begins to emerge that the idea that we can (i) characterize a logical set as “the extension of some predicate … or property” while (ii) not collapsing the idea of a logical set into the notion of a combinatorial set depends on cheating a bit by blurring the predicate/property distinction. We need something predicate-like to give us e.g. the Boolean operations; we need something sufficiently natural-property-like to avoid the unwanted collapse. So what’s the honest story about logical collections as extensions going to be? Let’s see what more Luca has to say!

To be continued

The post Luca Incurvati’s Conceptions of Set, 13 appeared first on Logic Matters.

From a small corner of Cambridge, 7

You don’t want my thoughts on the current political mess. So here’s a peaceful photo of St John’s chapel instead, taken from across Jesus Green on our morning walk. Once upon a time at this hour, there would early-morning rowers on the path, furiously cycling back from boathouses on the river. Now the Green is almost deserted.

So the university is planning for all lectures to be given online for the next academic year. Supervisions and small classes will continue, but no large group teaching for over a year from now. Not unexpected. After all, it is difficult to imagine anyone sensible wanting to be in an unnecessary crowd for a good while. But that decision close to home is a not-so-very-cheering reminder that we are indeed surely in for a long haul.

So I imagine that we won’t be going to concerts, for example, for many months. It’s really good to see, then, that Wigmore Hall are planning a series of twenty lunchtime concerts (one or two performers and no audience, broadcast live and then available for video streaming) for a month starting next week.   I wonder, though, if they are telling us something in having the series culminating  by rending our hearts in a performance of Winterreise? In the meantime, though, some unalloyed musical pleasure. The Chiaroscuro Quartet have released a disc of the first three of Haydn’s late great Op. 76 quartets. This is wonderful music (of course!) and here played with same insight and verve and delight and (appropriately!) light and shade as the Chiaroscuro’s earlier recording of the Op. 2o quartets. If anything will relieve the gloom of these troubled days for an hour, and then for more hours of repeated listening, then this is it! Warmly recommended.

The post From a small corner of Cambridge, 7 appeared first on Logic Matters.

Luca Incurvati’s Conceptions of Set, 12

We turn then to Chapter 6 of Luca’s book, ‘The Stratified Conception’.

This chapter starts with a brief discussion of Russell’s aborted ‘zigzag’ theory, which tries to modify naive comprehension by requiring that it applies only to sufficiently “simple” properties (or rather, simple propositional functions). It seems that Russell thought of the required simplicity as being reflected in a certain syntactic simplicity in expressions for the relevant properties. But he never arrived at a settled view about how this could be spelt out. It is only later that we get a developed set theory which depends on the comprehension principle being constrained by a syntactic condition. In Quine’s NF, the objects which satisfy a predicate A form a set just when A is stratifiable — when we can assign indices to its (bound) variables so that the resulting A* would be a correctly formed wff of simple type theory. And so the rest of Chapter 6 largely concerns NF.

Luca also touches on NFU, the version of Quine’s theory which allows urelemente. And — though this is a matter of emphasis — I’m was a bit surprised that the main focus here isn’t more consistently on this version. At the beginning of the book, Luca seems to hold that the most natural form of a set theory should allow for individuals: thus he describes the iterative conception (for example) as being of a universe which starts with individuals, and then builds up a hierarchy of sets from them. And if, when considering its technical development, we then concentrate on an iterative set theory without individuals, that’s because of easy equi-consistency results: adding urelements to ZFC’s theory of pure sets doesn’t change the scene in a deep way, so for many purposes it just doesn’t matter whether we discuss ZFC or ZFCU. But, famously, it isn’t like this with NF vs NFU. The consistency status of NF is still moot (Randall Holmes claims a proof, but its degree of opacity remains extremely high), and NF is inconsistent with Choice. While NFU is well known to be consistent and is consistent with Choice. Thus Holmes himself writes of NF and its variants that “only NFU with Infinity, Choice and possibly further strong axioms of infinity … is really mathematically serviceable.” That’s perhaps a judgement call, given Rosser’s earlier work on maths within NF. But it is certainly arguable that NF is something of a curiosity, while NFU wins mathematically. And given that it is more natural anyway in allowing for individuals, I’d have rather expected that NFU would have been the stratified theory for Luca to choose to really highlight.

Some would say that a chapter called ‘The Stratified Conception’ must be mistitled — for there isn’t really a conception of the set-theoretic world at work here! In §6.4, Luca talks of the ‘received view’ of NF(U) as being, precisely, a set theory which lacks conceptual motivation. Thus he quotes D. A. Martin calling it “the result of a purely formal trick … there is no intuitive concept”. Boolos writes that NF “appear[s] to lack a motivation independent of the paradoxes”. Fraenkel said “there is no mental image of set theory” which leads to NF’s characteristic axiom. If the received view is right, then Luca’s chapter could be very short!

But after outlining NF (and some of its oddities!) in §6.2, putting it into the context of the paradox-avoiding choice between indefinitely extensibility and universality in §6.3 (NF chooses the second), and noting the received view in §6.4, Luca turns in §6.5 to describe the path from type theory to NF. To negotiate the annoying repetitions of e.g. cardinal numbers at each type, Russell had already adopted a policy of using untyped claims which are to be read as typically ambiguous. So allowed instances of comprehension should be stratifiable though the explicit type indications are dropped. Then, as Luca explains, it is a rather natural step to consider keeping the stratifiable instances of comprehension while no longer supposing that stratifications are ontologically significant — i.e. we collapse the ontological type hierarchy into a single untyped domain. Which is what NF does (and indeed the theory is equiconsistent with adding to the simple theory of types an axiom schema that registers type ambiguity by saying that a typed wff is equivalent to the result of raising the types of all variables in that wff by one). So — contra the ‘received view’ (though in fact this is quite well known) — there is a pretty natural route which ends up with NF(U).

So far so good. But while observing that we can arrive at NF(U) by collapsing types gives the theory some motivation, more than the ‘received view’ allows, that doesn’t yet give us a positive conception of the resulting world of sets. More needs to be said: and that’s going to be the business of Luca’s §§6.6 and 6.7, to be discussed in the next post.

But first, it is perhaps worth noting that NFU can be developed without initially introducing the stratifiability condition at all (well, I find this intriguing!). Here I’m thinking of the axiomatization for set theory given by Randall Holmes in his Elementary set theory with a universal set. The domain contains atoms, sets, and (primitive) ordered pairs. Assume as fixed background that (i) extensionality holds for sets, (ii) atoms have no members. And now consider the following bunches of axioms:

Axioms telling us that the sets form a Boolean algebra — there’s the empty set at the bottom, the universal set at the top, every set has a complement, any two sets have an intersection and a union which is also a set.
An axiom of set union of the usual kind (given a set A of sets, there’s a set which is the union of the members of the members of A).
Some axioms telling us that every object has a singleton. Some axioms telling us that for any two objects there is an ordered pair of them, and that pairs and projections from pairs behave sensibly. Some axioms telling us sets have Cartesian products, and that binary relations as sets of ordered pairs behave sensibly.

So far, this might look to be a pretty natural base theory if we are trying to articulate a conception of sets which allows sets to behave the Boolean way we naively expect, and also allows a few familiar elementary constructs in the theory of relations and functions. Now suppose we add to the base theory two more specific axioms. These might not be ‘axioms we first think of’ but the first looks entirely unsurprising as a set-theoretic truth; and while the second gives us a set which is ‘too big’ by limitation-of-size principles, if we are going to buy a universal set, then this seems a reasonably natural assumption too.

For any relation, there is a set of the singletons of the objects that stand in that relation.
The pairs (x, y) where x is a subset of y form a set.

And now here’s the pay-off. A theory with these axioms proves NFU’s stratified comprehension axiom as a theorem. And (still assuming the fixed principles (i) and (ii)), stratified comprehension gives us everything else except the defining axioms for pairs. I’m not quite sure what to make of this result. But it might suggest that we can also motivate a route to NFU that doesn’t depend on what could perhaps still look like trickery with types.

To be continued.

The post Luca Incurvati’s Conceptions of Set, 12 appeared first on Logic Matters.

Guest post: Thomas Forster on Conceptions of Set and motivating NF

The next chapter of Conceptions of Set discusses set theories like NF that modify naive comprehension by imposing a stratification condition. My friend Thomas Forster, NF-iste extraordinaire, has been looking at some of Luca’s book too, and dropped me this note, which I thought it would be good to share here.

The usual on dit about stratification is that it has no semantics. This is the kind of thing people go around saying. And, as Luca points out, it simply isn’t true. There is this theorem of mine (building on work of Petry and Henson) that says that the stratifiable formulae are precisely those that are invariant under Rieger-Bernays permutations. I’m pretty sure that Dana Scott knew this result ages ago but didn’t feel the need to write it out. Henson must have known it too. I wrote it up and published it because it seemed to me that it mattered and that it should be brought out into the open. And that the on dit needed to be knocked on the head.

Here is another way of making the same point. There is the di Giorgi picture of (structures for the language of) set theory. A structure for the language of set theory is a set equipped with an injection into its power set (after all, a structure for the language of set theory is a set with an extensional relation on it, and an extensional relation on X is an injection from X into its power set [see my Logic, Induction and Sets, esp. §8.1]). We can think of this picture as each member of the set “coding” a subset of the set. Now Cantor’s theorem tells us that no such injection can be surjective. So some subsets must be left uncoded. So, in constructing a structure for the language of set theory, one has two steps to take. (i) One decides which sets are to be left out, and then (ii) one decides which surviving sets are to be coded by which elements. Natural question Q: which sentences have their truth-values already determined by stage (i)? That is, what sentences have the feature that their truth-values are determined purely by our decision about which subsets are going to be coded, and are not affected by our decision about which subsets are coded by which elements? Some examples are obvious. The structure believes the empty set axiom iff the empty set is in the range of the injection. The structure believes that every set has a singleton iff, whenever s is a subset that is coded, then the singleton of the element coding s is also a coded subset (never mind what the coding is). Answer to Q (of course): the stratified sentences!

But there is a larger question here. The Petry-Henson-Forster theorem relates one particular kind of invariance to one particular syntactic feature (namely stratification). In this case, it’s invariance under change of implementation. But there are other kinds of implementation-insensitivity, and typing systems that accompany them. There are people who understand the axiom scheme of replacement (not very many, it has to be said) and how it is all about implementation insensitivity. Here is an example: Does it make any difference to the abstract theory of ordinals you get whether you use von Neumann ordinals or Scott’s trick ordinals? It shouldn’t! But if you want to prove that it doesn’t then you need replacement.

Tomorrow, I hope, back to me on Luca’s chapter on NF.

The post Guest post: Thomas Forster on Conceptions of Set and motivating NF appeared first on Logic Matters.

Tim Button’s Set Theory: A Open Introduction

Tim Button wrote up his Cambridge lecture notes for a course on set theory for philosophers, previously taught by Michael Potter and then Luca Incurvati, as Open Set Theory which he then contributed to the Open Logic Project, and the resulting Set Theory: An Open Introduction can now be downloaded from this page on the Project’s site. The result, as you would expect from this author, is very good. It makes an excellent, and free, alternative to e.g. Enderton’s famous introductory book. It is particularly clear in marking off the initial informal (naive) development of the theory of sets, cardinals, ordinals etc. from the ensuing elaboration of an official iterative conception of the hierarchy and the formal development of an axiomatization of ZFC. It is perhaps just occasionally uneven in level; but when I do a half-yearly update of the Teach Yourself Logic Study Guide in a few weeks time, this will get promoted to a top recommendation.

I’ll be checking out again more of Open Logic’s offerings, for this project seems to have developed very well. In particular, I’ll also be recommending Richard Zach’s Incompleteness and Computability, which you can download here. More in TYL 2020.5. 

The post Tim Button’s Set Theory: A Open Introduction appeared first on Logic Matters.

Luca Incurvati’s Conceptions of Set, 11

We are continuing to discuss Luca’s Chapter 5. The naive comprehension principle — for every property F, there is a set which is its extension — seems intuitively appealing but leads to paradox. So how about modifying the principle along the following lines: for every good property F, there is a set which is its extension (a set of Fs)? Such a principle might inherit something of the intuitive appeal of the unmodified naive principle, but (with a suitable choice of what counts for goodness) avoid contradiction. So what could make for goodness, here? One suggestion that goes back to Cantor, Russell, and von Neumann, is that a property F is good if not too many things fall under it — in other words, we should modify naive comprehension by imposing what Russell called a ‘limitation of size’. How should the story then go?

In §5.2 and §5.3 Luca carefully explores the roots of the Cantorian idea that F is a good property if there are fewer Fs than ordinals. In §5.4. we then meet a proposal inspired by remarks of von Neumann’s: F is good if there are fewer Fs than sets. Luca then goes on to discuss one familiar way of implementing the von Neumann approach, famously explored by Boolos. We add to second order logic a Frege-like abstraction principle that says (roughly) that, when F and G are good, if everything which is an F is a G and vice versa, then the set of Fs is the set of Gs.

Logic Matters.

Luca Incurvati’s Conceptions of Set, 10

I’m picking up Luca’s book again, at Chapter 5. In the previous chapter, the question was: can we save the naive conception of set from ruin by tinkering with our logic? Short answer: no, not in a well-motivated way that will leave us with a set theory worth having. In this chapter, the question is: can we save the essence of the naive conception while retaining classical logic by minimally restricting naive comprehension?

Quine wrote:

Only because of Russell’s paradox and the like do we not adhere to the naive and unrestricted comprehension schema […] Having to cut back because of the paradoxes, we are well advised to mutilate no more than what may fairly be seen as responsible for the paradoxes.

Which suggests a simple-minded approach. Take one step back from disaster, and just accept all the instances of comprehension that do not generate paradox.

But what would that mean? First option: we should severally accept each instance of comprehension that does not entail contradiction. But it is easy to see that this is won’t work, because instances of comprehension which — taken separately — are consistent can together entail contradiction. Luca gives nice examples.

Second option, and surely more in keeping with Quine’s intention: we should accept those instances of comprehension which taken together do not entail contradiction. But this idea too doesn’t work.

As Luca points out, the proposal now is reminiscent of another paradox-avoiding proposal: be almost naive about truth by accepting just the maximal consistent set of all the instances of the T-schema. But McGee has a nice argument showing that that idea won’t wash; and Luca with Julien Murzi has generalized McGee’s argument so it applies here.

As a warm up, we can show that a maximally consistent set of instances of naive comprehension that e.g. includes the claim that there is an empty set is negation complete and hence (assuming the resulting set theory interprets Robinson arithmetic, a very weak demand!) is not recursively axiomatizable. Now, Luca says that such a set of instances can then hardly count as a set theory; but I’m not quite sure how much that would worry Quine. OK, any nicely axiomatized subset of that maximally consistent won’t be the full story about sets; but if we regiment enough of those consistent instances of comprehension into a theory rich enough for the working mathematician’s ordinary set-theoretic purposes (extending the theory if and when needed), why worry? We have a working theory (in one familiar sense), and a supposed story about why it is nice, i.e. it is part of the maximal naive set theory (in another familiar sense).

But let’s not pause over the hors d’oeuvre: the main course is the demonstration that (as in the case with instances of the T-schema) there after all there isn’t a unique maximal consistent set of all the instances of naive comprehension. Well, you might think that that too wouldn’t be too disastrous if the possible divergences between consistent stories were remote from ordinary business. But no such luck — uniqueness fails as badly as possible:

For any consistent sentence σ, there is a maximally consistent set of instances of naive comprehension implying σ, and another one implying ¬σ.

So the proposal to look for a maximal consistent set of instances of naive comprehension fixes no determinate theory at all (axiomatizable or otherwise). Hence the simple-minded reading of Quine’s one-step-back-from-disaster is indeed simply hopeless.

Two pernickety quibbles. The McGee 1992 paper in the biblio is the wrong one, it should his ‘Maximal Consistent Sets of Instances of Tarski’s Schema (T)’ in JPL. And the beginning of the Appendix on the Incurvati/Murzi upgrade of McGee’s theorem isn’t as clear as it ideally could be: e.g. a reader will pause to wonder what 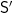is. But the argument of §5.1 indeed seems conclusive. The rest of this chapter is then about  ‘limitation of size’ principles. So let’s pause here and consider them in the next post.

The post Luca Incurvati’s Conceptions of Set, 10 appeared first on Logic Matters.

Hope in lockdown

To mark forty days of lockdown in the UK, Stile Antico created this socially-distanced recording of Thomas Tallis’ forty-part motet, Spem in alium, using smartphones and tablets.

The post Hope in lockdown appeared first on Logic Matters.

From a small corner of Cambridge, 6

We have at last ventured from our small corner of the city into centro storico on our morning walk: it was almost deserted. Here is a glimpse of Trinity and its Newtonian apple tree — without the dozens of tourists who are usually to be seen sitting along that low wall. Cambridge gets about eight million visitors a year, mostly on day trips (which is pretty absurd as there is really so little to see apart from King’s College Chapel, as most of the older colleges are closed to visitors most of the time). I imagine that very many residents would be pretty happy if that level of mass tourism doesn’t return here for years, if ever. But that’s just one more unknown about the post-virus world.

Meanwhile, no visit this week to Wigmore Hall on Tuesday to see the Pavel Haas, no driving off  today down to St. Mawes in Cornwall for the planned fortnight. Drat. But those are small things in the overall scheme; we are daily reckoning up our good fortune compared with so very many, and just keeping ourselves safe. And the preternaturally good spring weather has been mighty cheering and made those morning walks a delight. So on we go, into this new normal, whatever it turns out to be.

We can, of course, get books delivered here by post. But where’s the fun in that? One small everyday pleasure we really miss is getting to second-hand charity bookshops; we much enjoy the serendipity, the chance discoveries. The wonderfully well-run and well-stocked Oxfam bookshop in Walden is a particular favourite, and in normal times we drop in there perhaps twice a month. And when in Cornwall, there is a terrific bookshop at the National Trust house at Trelissick near St. Mawes. A couple of years ago, we happened to be there when someone came in to donate a paperback set of Helen Dunmore’s first ten novels (obviously brand new); I snapped them up within a minute, having by chance just finished and much admired one of her later novels, Exposure. I have been reading those earlier novels with great pleasure over the intervening months. And I’ve just finished Counting the Stars, Dunmore’s imagining of Catullus and his obsession with Clodia. I’m not sure that this is her most successful novel; and arguably her Catullus — for all his obsession — seems a mite too tame, lacking some the fury and satiric energy that drives the poetry. But I can still recommend it for a spring evening read, far from Rome!

The post From a small corner of Cambridge, 6 appeared first on Logic Matters.

Topology: A Conceptual History

‘In the history of mathematics the twentieth century will remain as the century of topology.’ (Jean Dieudonné).

That remark may be something of an exaggeration; but perhaps not by very much. And, by any reckoning, philosophers of mathematics ought to be especially interested in the development of topology over the century. It provides such a rich set of case studies in the way new mathematical concepts emerge and are developed, and in the way that new problems and new methods become adopted as canonical.

The trouble, of course, is that it isn’t easy to get a handle on the conceptual development of topology. I.M. James has edited a History of Topology, which weighs in at over a thousand pages, comprising forty essays of decidedly mixed quality and interest. Dieudonné has written A History of Algebraic and Differential Topology, 1900 – 1960, another six hundred pages or more, much of it pretty impenetrable to anyone other than a serious topologist. Then there is a three volume Handbook of the History of General Topology — another daunting twelve hundred pages, and pretty difficult to extract out any nuggets of philosophical interest.

As far as I know, however, there is nothing earlier which does the job of Topology: A Conceptual History. This book doesn’t at all pretend to be a comprehensive and fine-detailed history, recording all the false starts and mis-steps and minor alley ways; it is more in the spirit of a Lakatosian rational reconstruction, done with verve and insight. And, by contrast, this approach does vividly bring out the main contours of some key conceptual developments in a way that e.g. the lumbering Handbook essays mostly don’t. Moreover we get to see this done at a level of some mathematical detail — it’s not just arm-waving — while still remaining relatively accessible (a modest amount of undergraduate mathematics should mostly suffice). So philosophers of mathematics will come away, for example, with at least some feel for what homotopy and homology theories are about — and hence acquire some better understanding of the way different areas of enquiry (in this case, topology and algebra) can hang together in deep ways. We also get along the way genuinely illuminating sketches of the contributions of major figures starting from Euler, Riemann and Möbius, noting a dozen more.

An impressive achievement, then, and done within a tolerable length too! So I’m going to greatly enjoy reading this book (and also following up the two or three seemingly well-chosen suggested short readings for each chapter). I plan to blog about all this here …

… if and when someone gets round to writing the needed Topology: A Conceptual History.

The post Topology: A Conceptual History appeared first on Logic Matters.