Peter Smith's Blog, page 116

Coffee culture

When I was a lad, a long while since, the usual English alternative to tea seemed to be a cup of a beverage known as ‘milky coffee’. Black coffee was suspiciously foreign or downright louche — and indeed had to be drunk as a bohemian pose rather than for enjoyment since the coffee itself seemed almostly universally awful and (the cost of beans being as it was) very weak.

Now of course, we have a sophisticated coffee culture here. Sort of.

Well, you can get a fairly decent espresso macchiato in Caffè Nero (if you gently nudge the barista to doing it properly — the clue is in the name, guys: mark with a just bit of steamed milk/foam, but don’t try to fill the espresso cup to overflowing!). But I couldn’t help but notice that today it wasn’t just the usual majority choice: everyone else in the busy place had either a huge cappuccino (four or five times the size of anything you’d get in Italy) or a giant mug of latte. Fifty-something years on, milky coffee still rules, OK?

TYL, #13. March version of the Guide

The March version of the Teach Yourself Logic Guide is now available to be downloaded. The February version was downloaded 750 times, so I guess it is well worth continuing to put effort into this project.  In reading around, I’m certainly finding it interesting to revisit some old acquaintances, and to get newly acquainted with some books that have been accusingly sitting on my shelves unread. Enjoy!

The new material in this month’s version of the Guide consists of entries (more or less a page long each) on three books. I have only posted a draft commentary on one of these three books here on the blog (you’ll see that I’m skipping forward in the chronological order, and I’ll be returning to some of the many other books published in the same period). Here are the summary verdicts:

‘Little Kleene’, i.e. his Mathematical Logic of 1967 (cheaply available from Dover). Do read Chapter 5 on computability, incompleteness, decidability and closely related topics. This is nicely done, complements Kleene’s earlier treatment of the same material in Introduction to Mathematics, and takes an approach which is interestingly different from what you will mostly see elsewhere.
Ebbinghaus, Flum and  Thomas Mathematical Logic (1978, 1994).  The core material in Part A of the book is covered better (more accessibly, more elegantly) elsewhere. Of the supplementary chapters in Part B, the two chapters that stand out as worth looking at are perhaps Ch. 9 on extensions of first-order logic, and Ch. 14 (though not easy) on Lindström’s Theorems.
Goldstern and Judah, The Incompleteness Phenomenon: A New Course in Mathematical Logic  (1995). The first two chapters of this book can’t really be recommended either for making a serious start on first-order logic or for revision. The third chapter could be used for a brisk revision of some model theory if you have already done some reading in this area. The final chapter about incompleteness (which the title of the book might lead you to think will be a high point) isn’t the most helpful introduction in this style — go for Leary’s Friendly Introduction instead — and on the other hand it doesn’t go far enough for revision/consolidatory purposes.

So, I’m being very picky again when it comes to the Big Books. There is warm praise to come, though! Watch this space …

Pavel Haas Quartet, Wigmore Hall

I’ve raved here about the Pavel Haas Quartet before. But we had another chance to see them live at the Wigmore Hall last night. And they were as terrific as ever.

The Quartet were on fire from the start, playing Schnittke’s String Quartet No.3 with passion, commitment, authority and utterly convincing musicality. The only flaw in the performance was that just before the end, Veronika Jaruskova broke a string: they had to stop and rewind a page or so before finishing. I would have been very happy to have heard a lot more again, and I can only hope they record this.

Then they played the Shostakovich String Quartet No.8 (a piece I know a great deal better). I have never heard a more emotionally overwhelming performance. To borrow a phrase from another reviewer on another occasion, “they seamlessly drifted between fervor and introspection”. The Pavel Haas seem to sit on stage in a tighter semi-circle than others, and the interaction between them is a wonder to watch and gives such emotional intensity to their playing.

The Shostakovich was perhaps the high point of the evening, even compared with what was to come after the interval, when we heard Beethoven’s Quartet in B flat Op.130 with the Grosse Fuge played as the final movement. Primed as we were by the Schnittke and Shostakovich, this late quartet sounded even stranger, more ‘modern’, than usual, and it was played with the same level of emotional drive. I have perhaps heard more wrenching performances of the Cavatina (from the Lindsays in particular), but then the Pavel Haas launched themselves into Grosse Fuge with more fire and extreme attack than even the Lindsays used to give it. Quite astonishing. The audience was besides itself at the end.

Takács Quartet in Cambridge

The best string quartet now performing? Many think so. Their discography is astonishing. So it was a simply wonderful chance to hear the Takács Quartet live in Cambridge last night in the very intimate surroundings of the Peterhouse Theatre which seats just 180. They played the two Quartets Op 51 by Brahms, and Haydn’s Quartet in D, Op 76 no. 5. Not, to be honest, a programme I was particularly looking forward to, Brahms not being a favourite of mine. But the performances were wonderful, with such rhythmic verve and expressive range, and I was much more convinced by the Brahms than I’d ever been before. While the Haydn was simply the most joyful experience. The audience were obviously bowled over, and the Takács seemed to respond warmly to the considerable intimacy of the setting, which must be unusual for them these days. Three cheers, and more besides, to the very generous donors who make the Camerata Musica series possible. Next up, András Schiff playing the last three Beethoven sonatas …

IGT2: a spotter’s guide

So here’s how to spot IGT2 out in the wild, lurking shyly on the bookseller’s shelves, trying to hide its gaudy plumage … Distinctive yellow flashes, and quite a bright green spine with white markings. Multi-coloured on the front. Thought you’d like to see.

OK folks: you just know you want one for yourself. Cambridge locals will find it already in the CUP bookshop (and can get 20% off the official price of £19.99 for the pbk, with their uni card). Amazon UK has it for 12% off and free delivery. Amazon USA has a rather more measly discount, and you’ll have to wait a few weeks for the book to arrive across the Atlantic. But it is still a bargain for a book that weighs in at xvi + 388 larger format pages, and even contains some timeless truths.

Now I’ve just got to finish  getting all the exercises up on the website …

Call for survey articles by philosophers in early career

Philosophia Mathematica seeks to publish half a dozen survey articles on current and emerging areas of interest in philosophy of mathematics written by early-career philosophers.

If you are interested, please submit a 500-word sketch of the area that you propose to survey, along with a CV containing details of your publications, to the editor, Robert Thomas by one of two deadlines, March 31 and September 30, 2013. (At March 31, submissions will be considered and some topics assigned. Until Sept. 30, further submissions will be considered as they arrive and may be assigned, subject to not duplicating a previous assignment.)

Inquiries are welcome. Publication will occur individually as articles are ready. Submissions of articles and shorter discussion notes on the subjects of special issues and any other topic in philosophy of mathematics are always welcome.

Maria João Pires: intimacy and intensity

Suppose, just suppose, that one of the very greatest and most loved actors of his (or her) generation was tackling one of the high peaks of the repertoire, returning perhaps to a previous near-triumph with a quarter of a century’s more experience. Every broadsheet would have extensive reviews, though telling most readers about a performance they will never see (even if in reach of London and in funds to make the journey), because the tickets have long since sold out. There will be interviews with the actor, even colour-supplement spreads. You know how it goes.

Now here is one of the very greatest  and most admired pianists of her generation, still at the very height of her powers, returning to Schubert’s last piano sonata, a quarter of a century after a very fine earlier recording. You would have thought that the broadsheets with arts pages would at least notice this major event. After all, nearly all their readers can afford the CD, so accessible that it will arrive at the click of a button. So here surely is something worth reviewing. Here too is perhaps an occasion for interviews, and retrospective pieces on a remarkable artist.

But no. As far as I’ve seen, nothing.

Which is not at all unusual these days. It is difficult  not to feel (as you do when look round your fellow concert-goers, noting all the grey heads) that slowly but inexorably a deep engagement with classical music is becoming less and less central to our cultural life.

Well here, let it be said, is the most extraordinary music-making, indeed inviting the most personal engagement. Maria João Pires offers us a performance of the A Minor Sonata D. 845  played with intense intimacy. There is nothing declamatory here: she is sitting across the room, playing for us listening, close around her. There’s a care to every phrase which isn’t mannered, wonderful lightness of touch when called for, and moments when time is slowed to a pause (her magical way with the Trio of the third movement). For this sonata alone you will want the disc.

But then there is D. 960. What is to be said? For many, this is very high on the list of  the music that matters the most, that has to be returned to time and again. We have a most wonderful inheritance of recordings from Schnabel onwards of this “music which … is better than it can be performed”. Brendel, Richter and Imogen Cooper, all more than once, Lupu, Kovecevich and Uchida — all are stunning in their different ways, all their recordings are to listened to repeatedly.  And Pires herself recorded the sonata 25 years ago.

It would be absurd (or at least absurd for me) to try to make comparisons. Let me just say that this new recording is surely a more than a worthy addition to that great inheritance. This is not one of those more brooding performances where we are made conscious from the beginning that this is the work of a dying man (performances which give the first movement such ominous weight as to unbalance the whole sonata). There is an intimate directness to her undeclamatory opening: again, we are sitting with Pires — she is not addressing us across a concert hall. And it is only slowly that the intensity is ratcheted up in the first movement (especially about 11 minutes in), and then we are gripped by a new tension as the opening theme and development return once more. The following Andante sostenuto is unsentimental, played with a rhythmic delicacy that becomes magical. The Scherzo is played vivace con delicatezza as Schubert asks: but Pires deconstructs the Trio with bass emphases which I can’t recall being made quite so aware of before,  harking back to previous movements. The final Allegro has moments of lightness again but also a certain weight and drive giving a more-than-satisfying balance to the whole sonata, the tumbling final chords finishing in a sudden silence.

This won’t replace your other recordings of D. 960, how could it? But you will want to listen and listen again, and you will hear more from Pires each time. Wonderful.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

TYL, #12. The Big Books — Goldstern and Judah 1995

Some 300 people have downloaded the February version of the Teach Yourself Logic Guide, so I guess I’m not entirely wasting my energy. Sure, the Guide won’t be a particular exciting project for many: so I must try to get back to blogging about more interesting stuff. But for those who are following, here — far out of chronological sequence — is a draft entry for the Big Books chapter on Goldstern and Judah’s The Incompleteness Phenomenon.

A number of people have recommended this book to me, so I thought I should take a closer look. Well, I have, and I wasn’t bowled over. What am I missing?

Half of The Incompleteness Phenomenon: A New Course in Mathematical Logic by Martin Goldstern and Haim Judah (A.K. Peters, 1995: pp. 247) is a treatment of first-order logic. The rest of the book is two long chapters of just the same length, one on model theory, one on incompleteness and a little on recursive functions. So the emphasis on incompleteness in the title is somewhat misleading: it is at least equally an introduction of some model theory. I have had this book recommended to me more than once, but I find myself immune to its supposed charms (I too often don’t particularly like the way that it handles the technicalities): your mileage may vary.

Some details Ch. 1 starts by talking about inductive proofs in general, then gives a semantic account of sentential and then first-order logic, then offers a Hilbert-style axiomatic proof system.

Early on, the authors introduce the notion of 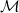-terms and 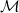-formulae. An 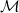-term (where 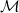is model for a given first-order language 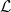) is built up from 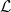-constants, 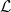-variables and/or elements of the domain of 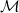, using 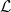-function-expressions; an 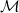-formula is built up from 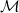-terms in the predictable way. Any half-awake student is going to balk at this. Re-reading the set-theoretic definitions of expressions as tuples, she will realize that the apparently unholy mix of bits of language and bits of some mathematical domain in an 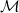-term is not actually incoherent. But she will right wonder what on earth is going on and why: our authors don’t pause to explain. (A good student who knows other presentations of the basics of first-order semantics should be able to work out after the event what is going on in the apparent trickery of Goldstern and Judah’s sort of story: but this isn’t the way to start, without adequate explication of the point of the procedure.)

Ch. 2 gives a Henkin completeness proof for the first-order deductive system given in Ch. 1. This has nothing special to recommend it, as far as I can see: there a lot of more helpful expositions available. The final section of the chapter is on non-standard models of arithmetic: Boolos and Jeffrey (Ch. 17 in their third edition) do this more approachably.

Ch.3 is on model theory. There are three main sections, ‘Elementary substructures and chains’, ‘ultra products and compactness’, and ‘Types and countable models’. So this chapter — less than sixty pages — aims quite high to be talking about ultraproducts and about types. You could read it after working through e.g. Manzano’s book: but I certainly don’t think this chapter makes for an illuminatingly accessible first introduction to serious model theory.

Ch. 4 is on incompleteness, and the approach here seems significantly more gentle than the previous chapter. The authors make things easier for themselves by adopting a version of Peano Arithmetic which has exponentiation built in (so they don’t need to tangle with Gödel’s beta function). And they only prove a semantic version of Gödel’s first incompleteness theorem (the authors don’t say anything about why we might want to prove the syntactic version of the first theorem, and don’t even mention the second theorem). The proof goes as by showing directly that — via Gödel coding — various syntactic properties and relations concerning PA are expressible in the language of arithmetic with exponentiation (in other words, they don’t argue that those properties and relations are primitive recursive and then show that PA can express all such properties/relations). But this isn’t done particularly well: I think this sort of more direct assault on incompleteness is better handled in Leary’s book (recommended in the Guide).

The book ends by over-briskly introducing the ideas of primitive recursive and recursive functions.

Summary verdict The first two chapters of this book can’t really be recommended either for making a serious start on first-order logic or for consolidatory reading. The third chapter could perhaps be used for a brisk revision of some model theory if you have already done some reading in the area. The final chapter about incompleteness (the title of the book might lead you to think that this will be a high point) isn’t a helpful introduction: it could be skimmed through to see how the authors approach things, but it doesn’t really go far enough for more serious purposes.

Teach Yourself Logic, #11. New version of the Guide

Right. I really must get on with other work (in particular the task of writing exercises for the Gödel book awaits).  But, as an exercise in constructive procrastination I’ve just uploaded the February 2013 version of the Teach Yourself Logic Guide.

Chapter 1 on The Basics is in a reasonably stable state, and I’ve only tinkered with that in small ways since the last version as uploaded back in November. I’ve added another section to Chapter 3, ‘Exploring Further’.  But the big change is that I’ve started work on the new Chapter looking at some of the Big Survey Books on mathematical logic. There’s quite a long list to work through — I must be mad to have taken this task on myself! — so don’t hold your breath waiting for the entry on your favourite book. Still, between you and me, it has been enjoyable to dive in, blow the dust off some old acquaintances, and remind myself what they get up to. So I do plan to continue adding entries sporadically.

I’ve added to the Guide the entries on the classic texts by Kleene, Mendelson and Shoenfield of which I posted drafts here. As a bonus I’ve also just added an additional entry on Joel Robbin’s 1969 book Mathematical Logic: A First Course. Yes, yes, that doesn’t really come next in chronological order and it isn’t exactly a Big Book either (the main text is just 170 pages). But it does cover an interesting amount in a short space. And having been a bit grouchy about Mendelson and very grouchy about Shoenfield, I’m inclined to be rather warm about this. My summary verdict is

A different route through this material [first- and second-order logic, primitive recursive arithmetic, PA2, Gödel's theorem], Robbin’s book is accessibly written and still worth reading. Look especially at Ch. 3 for the unusually detailed story about how to build a language with a function expression for every p.r. function, and at the last chapter for how to work in PA2.

For more details, see the Guide!

Teach Yourself Logic, #11. New version of the Guide (plus something on Robbin 1979)

Right. I really must get on with other work (in particular the task of writing exercises for the Gödel book awaits).  But, as an exercise in constructive procrastination I’ve just uploaded the February 2013 version of the Teach Yourself Logic Guide. Chapter 1 on The Basics is in a reasonably stable state, and I’ve only tinkered with that in small ways since the last version uploaded back in November. I’ve added another section to Chapter 3, ‘Exploring Further’.  But the big change is that I’ve started work on the new Chapter looking at some of the Big Survey Book. There’s a long list to work through — I must be mad to have taken this on! — so don’t hold your breath waiting for the entry on your favourite book. Still, it has been enjoyable to dive in, blowing the dust off some old acquaintances, and reminding myself what they get up to. So I plan to continue adding entries sporadically.

I’ve put into the Guide the entries on the classic texts by Kleene, Mendelson and Shoenfield for which I posted drafts here. As a bonus I’ve also just added an additional entry on Joel Robbin’s 1969 book Mathematical Logic: A First Course. Yes, yes, that doesn’t really come next in chronological order and it isn’t exactly a Big Book either (the main text is just 170 pages). But it does cover an interesting amount in a short space. And having been a bit grouchy about Mendelson and very grouchy about Shoenfield, I’m inclined to be rather warm about this. My summary verdict is

A different route through this material [first- and second-order logic, primitive recursive arithmetic, PA2, Gödel's theorem], Robbin’s book is accessibly written and still worth reading. Look especially at Ch. 3 for the unusually detailed story about how to build a language with a function expression for every p.r. function, and at the last chapter for how to work in PA2.

For more details, see the Guide!