Peter Smith's Blog, page 113

‘The contemporary conception of logic’, #2

A month ago I posted here a quick comment on some remarks of Warren Goldfarb’s about ‘the contemporary conception of logic’, in particular about the special role (supposedly) given to schemata in the definition of some key logical concepts. I’ve since found that David Bostock in his recent book on Russell’s logical atomism takes pretty much the same line about ‘logic as it is now conceived’. They are, in effect, projecting Quine’s somewhat idiosyncratic views onto the wider logical community.

Their remarks have provoked me into dipping into standard mathematical logic texts, from Mendelson onwards. The headline news is that only one such book I looked it — in fact, Mendelson’s — takes the line that Goldfarb and Bostock think characteristic of modern logic.

Which isn’t to deny that there are important differences between Frege’s approach to logic (Goldfarb’s concern) and Russell’s approach (Bostock’s interest), on the one hand, and most contemporary logicians on the other. But it does suggest that whatever is to be put on our side of the contrast, it isn’t a matter of us moderns typically giving schemata a special role in our very definitions of key logical properties like validity.

I have written up some working notes on this, giving some details of what happens in various canonical modern math. logic texts — with more detail on the first few books chronologically (as they happen to cover most of the available options), and then speeding up as my excitement wanes. You can download the notes here.

Back to Gödel Without Tears — but not a MOOC

For a number of years, when I taught a course on Gödel’s incompleteness theorems, I distributed handouts, which — as is the way of these things — grew and grew and eventually became early drafts of An Introduction to Gödel’s Theorems. But when it was eventually published, even the first edition of the book was over 350 pages long. So I then found myself writing another set of handouts for classroom use, an introduction to the Introduction, as it were! The most recent version of those handouts has been freely available here for a couple of years as Gödel Without (too many) Tears, and this has been downloaded about 4000 times.

Well, since GWT was last revised, I’ve put together a second edition of the Gödel book;  so it would be useful to now update GWT (and to add some sections to correspond to the final chapters of the book as well). So here’s a plan.

Starting on Monday 15th October, I’ll be posting eight weekly instalments of a new version of Gödel Without (too many) Tears. This first tranche should take us up to the First Theorem. Then we’ll start again in the new year on Monday 20th January with another eight instalments.

The dates happen to be chosen to fit term dates here in Cambridge, but also (rather more importantly) to spread the load for me. Much better to commit to a slow delivery, than promise to rattle through faster and then not keep to schedule.

 I’ll try to ensure that these freely available notes can be used as a stand-alone introduction to the incompleteness theorems as well as being an accompaniment to the second edition of the book. So this will be a sort of online course. Not an official MOOC, though, but something very much more informal. No teaching assistants grading stuff, no online tests, no accreditation — just some reader-friendly PDFs, maybe a short video or two, and intellectual fun to be had!

Still, I’ll no doubt be happy to give at least some backup and make some responses to queries. I’m still thinking a bit about how and where best to do that. I don’t particularly want to faff about e.g. setting up special discussion forum software on the logicmatters site. So one option would be to use an external service like ProBoards.com. Another option would be to keep things even simpler: invite reports of typos, thinkos, or obscurities in the appropriate comments boxes on pages here, and suggest that anyone with a substantive question which might be of more general interest ask it on math.stackexchange.com (where, with luck, I won’t be the only person answering — so you could get a helpfully different angle on some sticking point). But I’d welcome thoughts about this.

Anyway, spread the word that this sort-of-a-course is coming up!

Chiaroscuro on BBC iPlayer

You can listen to their Edinburgh Festival concert on BBC iPlayer for a few days. Their performance of the Schubert “Rosamunde” quartet — starting at 1.08 in from the beginning of the transmission — seems even better than their CD recording. Which is saying quite something.

Next post, back to logic. Promise!

The Chiaroscuro Quartet again

We went with high expectations to hear the Chiaroscuro Quartet playing in the Summer Music Festival in Cambridge on Saturday, but we were completely bowled over. They are just wonderfully good. If the quartet is playing near (or not so near) you sometime, buy the tickets and go! And buy their recordings too.

I should have noticed from the pictures on their website — here they are in rehearsal — that they perform standing up (apart from the cellist, of course) and very close to each other. The two violinists in particular almost dance together in their expressive movement, and the ensemble between all four players is quite extraordinary. The quartet most certainly isn’t a star vehicle for Alina Ibragimova, but as ideally balanced as you’d hope. And interestingly, their sound in concert seems rather richer and warmer than on their CDs (they play on gut strings tuned at lower than modern pitch, and their recordings perhaps emphasize the unusual timbre).

They played the Mozart E flat Quartet, K428 (which the Quartet have recorded on their second CD), which was predictably terrific. And after the interval came the eighteen year old Mendelsson’s string Quartet (Op. 12, no. 2) — despite the numbering, his first written quartet. We hadn’t heard this for perhaps twenty years, and it was a delight. But the real revelation of the evening was the first piece they played, Haydn’s A major Quartet, Op. 20, no. 4. This was how Haydn should be played, with dancing lightness, grace, and utter musicality. Magical. As, judging from their applause, the whole audience surely recognized.

Is this how it was for you?

In the shop window you have promptly identified the cover with the title you were looking for. Following this visual trail, you have forced your way through the shop past the thick barricade of Books You Haven’t Read, which were frowning at you from the tables and shelves, trying to cow you.

But you know you must never allow yourself to be awed, that among them there extend for acres and acres the Books You Needn’t Read, the Books Made For Purposes Other Than Reading, Books Read Even Before You Open Them Since They Belong To The Category Of Books Read Before Being Written. And thus you pass the outer girdle of ramparts, but then you are attacked by the infantry of the Books That If You Had More Than One Life You Would Certainly Also Read But Unfortunately Your Days Are Numbered. With a rapid maneuver you bypass them and move into the phalanxes of the Books You Mean To Read But There Are Others You Must Read First, the Books Too Expensive Now And You’ll Wait Till They’re Remaindered, the Books ditto When They Come Out In Paperback, Books You Can Borrow From Somebody, Books That Everybody’s Read So It’s As If You Had Read Them, Too. Eluding these assaults, you come up beneath the towers of the fortress, where other troops are holding out:

the Books You’ve Been Planning To Read For Ages,

the Books You’ve Been Hunting For Years Without Success,

the Books Dealing With Something You’re Working On At The Moment,

the Books You Want To Own So They’ll Be Handy Just In Case,

the Books You Could Put Aside Maybe To Read This Summer,

the Books You Need To Go With Other Books On Your Shelves,

the Books That Fill You With Sudden, Inexplicable Curiosity, Not Easily Justified.

Now you have been able to reduce the countless embattled troops to an array that is, to be sure, very large but still calculable in a finite number; but this relative relief is then undermined by the ambush of the Books Read Long Ago Which It’s Now Time To Reread and the Books You’ve Always Pretended To Have Read And Now It’s Time To Sit Down And Really Read Them.

With a zigzag dash you shake them off and leap straight into the citadel of the New Books Whose Author Or Subject Appeals To You. Even inside this stronghold you can make some breaches in the ranks of the defenders, dividing them into New Books By Authors Or On Subjects Not New (for you or in general) and New Books By Authors Or On Subjects Completely Unknown (at least to you), and defining the attraction they have for you on the basis of your desires and needs for the new and the not new (for the new you seek in the not new and for the not new you seek in the new).

All this simply means that, having rapidly glanced over the titles of the volumes displayed in the bookshop, you have turned toward a stack of An Introduction to Gödel’s Theorems fresh off the press, you have grasped a copy, and you have carried it to the cashier so that your right to own it can be established.

You cast another bewildered look at the books around you (or, rather: it was the books that looked at you, with the bewildered gaze of dogs who, from their cages in the city pound, see a former companion go off on the leash of his master, come to rescue him), and out you went.

(As Italo Calvino almost puts it, at the beginning of ‘If on a winter’s night a traveler’.)

Cloud storage made easy: with a bit of helpful geekiness

This may be useful for someone who like me doesn’t keep up with every geeky development, and so can miss out on things (thanks to Keith Frankish for the heads-up).

OK: you know that it makes sense to back up a lot of your stuff “in the cloud” (we’ll set aside questions of security and sensitive personal stuff — I’m talking about all the rest).  At this late date, you don’t need a lecture about backing up from me!  And you very likely know about the delights of Dropbox. But maybe you are running out of free space. Or you just want to be doubly secure. What to do (without paying out for a “premium” account)?

Well, you could try the new cloud storage service at copy.com, which is about two months old, and aims to muscle in on Dropbox. Sign up by clicking on this link and you’ll get 20GB of free storage [and -- full disclosure -- I get 5GB extra storage for every sign-up if you do the email verification to kick things off]. I suspect this is a time-limited early-adopters generous offer to help spread the word. Give it a whirl, as you’ve nothing to lose. Signing up involves no more than choosing a password, downloading an app, and clicking a verification link in an email — nothing scary.

Then what happens? A folder “Copy” is installed, and while the app is running what you put in the folder gets automatically copied to the cloud  (you can sync across machines, and can access contents from the cloud from mobile apps — the usual kind of thing you’d expect). Why not give it a go, to increase your cloud storage?

“Ah, but I don’t want to muck about with my folder system and/or I’ve already got a Dropbox folder for stuff I want to backup in the cloud”.  No problem. Here’s the promised helpful geekiness:  you don’t actually have to move files or folders into the Copy folder — you can just put into that folder a symbolic link to anything you want backed up. E.g. a symlink to your “Current work” folder, or to your iPhoto library, or whatever.  (“What’s a symbolic link?” Not an alias — you can Google the difference. The key thing is that a symlink is transparent to Copy and to Dropbox, so putting a symlink into your Copy and/or your Dropbox folder is as good as putting a copy of the file into the folder, except it takes up no space on your hard drive and the copy changes when the file does. Mac users can make symbolic links exceedingly easily using this. )

You can thank me later …

I missed this exchange about Analysis …

I missed this exchange about Analysis, in which a couple of nice things are said about a certain one-time Editor. Heavens, though — what a time-consuming task that editing malarky was …

‘The contemporary conception of logic’

Warren Goldfarb, in his paper ‘Frege’s conception of logic’ in The Cambridge Companion to Frege, announces that his ‘first task is that of delineating the differences between Frege’s conception of logic and the contemporary one’. And it is not a new idea that there are important contrasts to be drawn between Frege’s approach and some modern views of logic. But one thing that immediately catches the eye in Goldfarb’s prospectus is his reference to the contemporary conception of logic. And that should surely give us some pause, even before reading on.

So how does Goldfarb characterize this uniform contemporary conception? It holds, supposedly, that

the subject matter of logic consists of logical properties of sentences and logical relations among sentences. Sentences have such properties and bear such relations to each other by dint of their having the logical forms they do. Hence, logical properties and relations are defined by way of the logical forms; logic deals with what is common to and can be abstracted from different sentences. Logical forms are not mysterious quasi-entities, à la Russell. Rather, they are simply schemata: representations of the composition of the sentences, constructed from the logical signs (quantifiers and truth-functional connectives, in the standard case) using schematic letters of various sorts (predicate, sentence, and function letters). Schemata do not state anything and so are neither true nor false, but they can be interpreted: a universe of discourse is assigned to the quantifiers, predicate letters are replaced by predicates or assigned extensions (of the appropriate arities) over the universe, sentence letters can be replaced by sentences or assigned truth-values. Under interpretation, a schema will receive a truth-value. We may then define: a schema is valid if and only if it is true under every interpretation; one schema implies another, that is, the second schema is a  logical consequence of the first, if and only if every interpretation that makes the first true also makes the second true. A more general notion of logical consequence, between sets of schemata and a schema, may be defined similarly. Finally, we may arrive at the logical properties or relations between sentences thus: a sentence is logically true if and only if it can be schematized by a schema that is valid; one sentence implies another if they can be schematized by schemata the first of which implies the second.

Note an oddity here (something Timothy Smiley has complained about in another context). It is said that a ‘logical form’ just is a schema. So what is it then for a sentence to have a logical form (as you can’t have a schema): presumably it is for the sentence to be an instance of the schema. But the sentence ‘Either grass is green or grass is not green’ — at least once we pre-process it as ‘Grass is green 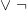grass is green’ — is an instance of both the schema 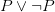and the schema . These are two different schemata: but surely no contemporary logician when thinking straight would say that the given sentence, for this reason at any rate, has two different logical forms. So something is amiss.

But let’s hang fire on this point. The more immediate question is: just how widely endorsed is something like Goldfarb’s described conception of logic? For evidence, we can take a look at some well-regarded math. logic textbooks from the modern era, i.e. from the last fifty years — which, I agree, is construing ‘contemporary’ rather generously (but not to Goldfarb’s disadvantage). We’d need to consider e.g. how the various authors regard formal languages, what they take logical relations to hold between, how they regard the letters which appear in logical formulae, what accounts they give of logical laws and logical consequence, and how they regard formal proofs. To be sure, we might expect to find many recurrent themes running through different modern treatments (after all, there is only a limited number of options). But will we find enough commonality to make it appropriate to talk of `the’ contemporary conception of logic?

Of course, I hope it will be agreed that this question is interesting in its own right: I’m really just using Goldfarb as a provocation go on the required trawl through the literature. I’ve picked off my shelves a dozen or so textbooks from Mendelson (1962) to (say) Chiswell and Hodges (2007), and it will be interesting to see how many share the view of logic which Goldfarb describes.

Preliminary report: to my surprise (as it isn’t how I remembered it) Mendelson’s conception of logic does fit Goldfarb’s account very well. At the propositional level, tautologies for Mendelson are a kind of schema (so aren’t true!); logical consequence is defined as holding between schemata; Mendelson’s formal theory is a theory for deriving schemata. Likewise, charitably read, for his treatment of quantificational logic. Moreover Mendelson avoids the unnecessary trouble that Goldfarb gets himself into when he talks of logical form: Mendelson too talks of logical structure, but he supposes that this is ‘made apparent’ by using statement forms, not that it is to be identified with statement forms. So 1/1 for Goldfarb.

So far so good. But chronologically the next book I’ve looked at is ‘little Kleene’ , i.e. Kleene’s Mathematical Logic (1967). And Goldfarb’s account doesn’t apply to this. For a start, Kleene’s 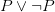 is not schematic but picks out a truth in some object language fixed in the context, as it might be Jack loves Jill or Jack doesn’t love Jill or  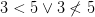Which (to cut the story short) makes the score 1/2.

I’ll let you know what the score is when I’ve looked at the other texts on my list …

The Chiaroscuro Quartet … what can one say?

The Chiaroscuro Quartet have a second CD out now — the Beethoven op. 95 “Serioso”, Mozart’s E flat K. 428 quartet, and Mozart’s Adagio and Fugue K. 546. This all strikes me as being as wonderful as their debut disk. The quartet perform “on period instruments, informed by an historical approach” which means, for a start, they play on gut strings, with minimal vibrato and tuned to A430. But don’t take against that! As Alina Ibragimova, the leader, has said, the quartet’s approach is “more about creating a rich sound world rather than being historically correct.” True, it takes a few minutes to get accustomed to the timbre; yet it makes for a freshness and clarity which is then utterly compelling.

In particular, I find their performance of the Schubert “Rosamunde” Quartet D.840 on their first CD just astonishing for a quartet so young and intensely moving (or is it moving because they are young and will take the risks?). There are some utterly wonderful recordings of the Schubert out there, including — pre-eminently, I would earlier have said — one by the Lindsays (recorded in 1987), which is almost matched by the Belcea (2002), and closely followed perhaps the Takács (2006). But the Chiaroscuro’s performance is just magical, haunting, intense and intimate. I’m not quite lost for words, but really the message has to be simply “Listen!”.

(Readers near Cambridge might like to know that the quartet are playing here on August 2nd.)

 

The Development of Logic, Mk III?

It’s now just over fifty years since William and Martha Kneale’s The Development of Logic was first published. The book is still in print, and there remains nothing quite like it. There’s a very great deal of scholarship revealed in the first four-hundred or so pages leading up to Frege, and those pages still read rather well, and remain a very helpful introduction. The pivotal role then given to Frege was not so usual at the time, and William Kneale’s discussion over some eighty pages was a boon to generations of students. The concluding chapters seem much more dated now, but overall the book remains a quite splendid achievement.

It would surely be near impossible now for a pair of authors to emulate the range of the Kneales from-Aristotle-to-the-present. At one end of the task, just think of the explosion of work on later Greek, Roman and medieval philosophy which would have to be engaged with. At the other end of the task, think how far logic has moved forward on how many fronts in the last half-century or so. It’s not surprising, then, a student looking for real breadth is now faced with multi-author blockbusters. The Handbook of the History of Logic has reached eleven volumes and something like 8000 pages(!). As is the way of such things, the quality and level of its entries varies wildly, with authors rather too keen to show off their expertise, so far too much will be beyond the reach of (the contemporary equivalent of) the student who once gratefully reached for The Development of Logic.

Even a recent multi-author volume of more restricted scope, Leila Haaparanta’s The Development of Modern Logic, runs at something like three times the length of the Kneale’s coverage of the same period. And this book seems to suffer particularly badly from a lack of editorial vision (how come the estimable Wilfrid Hodges writing on ‘Set Theory, Model Theory, and Computability Theory’ (yes, all three!) is confined to 28 pages, while Andrew Aberdein and Stephen Read get 111 pages on ‘The Philosophy of Alternative Logics’?). There’s some useful material here, but it’s no update of the Kneale’s book.

I rather think, then, that there is a gap here waiting to be filled by, shall we call it, The Development of Modern Logic: from Frege to Tarski — a single-author book aimed at advanced undergraduates or beginning graduate students in philosophy (and mathmos who care about such things). Pre-Frege, the coverage could be fairly minimal. And the book could still stop (in effect) roughly when the original The Development of Logic stops.

Why so? The Kneales write in their preface “our primary purpose has been to record the first appearance of those ideas which seem to us most important in the logic of our own day”. Now I’m not so sure how illuminating it is to dig down to first appearances of ideas, especially given that the founding fathers of modern logic were so ignorant/dismissive of their predecessors. (To be sure, it is quite fun to know something of what there is to know about Chrysippus, for example: but it won’t help you to understand any better Frege or Russell or Hilbert or the rest. Or to jump to another example, Bolzano deserves credit for his story about logical consequence: but it was buried in obscurity and had little direct influence.) On the other hand, however, I do think that the Kneale’s officially Whiggish approach (which they don’t themselves stick to at all closely) can be a helpful way to go. To be sure, it is not the only sort of history worth doing: but it is one illuminating route to take. After all, around forty years ago, more or less, a certain conception of what constitutes the core of modern logic gets entrenched. The question arises: how and why did we get from Frege’s founding document, the Begriffsschrift, to the entrenched modern conception? Exploring this is a narrow enough project to be carried out in a reasonable-sized, accessible, book, but surely interesting enough to be a very worth-while exercise.

After all, it isn’t that easy for students e.g. to find out what happens logically in Principia, or e.g. to discover. just what Hilbert’s contribution to the development of logic was, or e.g. to understand how Gödel could prove the semantic completeness of first-order logic years before Tarski had nailed down the semantics.

So, as I say, I rather think that the project of writing in a student-friendly way about the development of logic from Frege to Tarski would be very worth doing. Maybe I should make a start. What do you think?