Peter Smith's Blog, page 117

Teach Yourself Logic, #10. The Big Books — Shoenfield 1967

I think I might be going to regret this. I’ve just realized that there are over 25 “Big Books” on math logic on my shelves that could reasonably warrant a mention in the planned chapter in the Teach Yourself Logic Study Guide. So no promises to get everything finished quickly! Still, the chronologically next entry writes itself pretty easily. So let’s get it out of the way.

Joseph R. Shoenfield’s Mathematical Logic (Addison-Wesley, 1967: pp. 334) has, over the years, also been much recommended and much used: it is officially intended as ‘a text for a first-year [maths] graduate course’. This is hard going, a significant jump up in level from Mendelson, though often the added difficulty in mode of presentation seems to me not to be necessary. The book can probably only be recommended to hard-core mathmos who already know a fair amount and can cherry-pick their way through the book. It does have heaps of hard exercises, and some interesting technical results are in fact buried there. But whatever the virtues of the book, they certainly don’t include approachability or elegance or student-friendliness in the early chapters.

In a bit more detail, Chs. 1–4 cover first order logic, including the completeness theorem. It has to be said that the logical system chosen is rebarbative. The primitives are , , 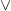, 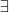and . Leaving aside the identity axioms, the axioms are the instances of excluded middle and instances of 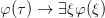, and then there are five rules of inference. So this neither has the cleanness of a Hilbert system not the naturalness of a natural deduction system. Nothing is said to motivate this horrible choice as against others.

Ch. 5 is an introduction to some model theory getting as far as the Ryll-Nardjewski theorem. But this will done far too rapidly for most readers (unless you are using it as a terse revision course).

Chs. 6–8 cover the theory of recursive functions and formal arithmetic. Schoenfield defines the recursive functions as those got from an initial class by composition and regular minimization. As elsewhere, ideas are presented in a take-it-or-leave-it spirit, and no real motivation for the choice of definition is given (and e.g. the definition of the primitive recursive functions is relegated to the exercises). Unusually for a textbook at this sort of level, the discussion of recursion theory in Ch. 8 goes far enough to cover a Gödelian ‘Dialectica’-style proof of the consistency of arithmetic, though the presentation is not particularly accessible.

Ch. 9 on set theory is perhaps the book’s real original raison d’être. It is a quarter of the whole text and was (if I recall right) the first extended textbook presentation of Cohen’s independence results via forcing, from four years previously. The treatment also touches on large cardinals. This was surely an admirable achievement in its time: but it is equally surely not now the place to start with set theory in general or forcing in particular, given the availability of later presentations. [Or at least, that was my first thought, based on memory: but I'm inclined to go back and revise judgement at least on the set theory chapter.]

Summary verdict Now only for very selective dipping into by already-well-informed enthusiasts.

Teach Yourself Logic, #10. The Big Books — Schoenfield 1967

I think I might be going to regret this. I’ve just realized that there are over 25 “Big Books” on math logic on my shelves that could reasonably warrant a mention in the planned chapter in the Teach Yourself Logic Study Guide. So no promises to get everything finished quickly! Still, the chronologically next entry writes itself pretty easily. So let’s get it out of the way.

Joseph R. Schoenfield’s Mathematical Logic (Addison-Wesley, 1967: pp. 334) has, over the years, also been much recommended and much used: it is officially intended as ‘a text for a first-year [maths] graduate course’. This is hard going, a significant jump up in level from Mendelson, though often the added difficulty in mode of presentation seems to me not to be necessary. The book can therefore only be recommended to hard-core mathmos who already know a fair amount and can cherry-pick their way through the book. It does have heaps of hard exercises, and some interesting technical results are in fact buried there. But whatever the virtues of the book, they certainly don’t include approachability or elegance or student-friendliness.

In a bit more detail, Chs. 1–4 cover first order logic, including the completeness theorem. It has to be said that the logical system chosen is rebarbative. The primitives are , , 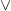, and . Leaving aside the identity axioms, the axioms are the instances of excluded middle and instances of 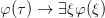, and then there are five rules of inference. So this neither has the cleanness of a Hilbert system not the naturalness of a natural deduction system. Nothing is said to motivate this horrible choice as against others.

Ch. 5 is an introduction to some model theory getting as far as the Ryll-Nardjewski theorem. But this is all done far too rapidly (unless you are using it as a terse revision course).

Chs. 6–8 cover the theory of recursive functions and formal arithmetic. Schoenfield defines the recursive functions as those got from an initial class by composition and regular minimization. Again, no real motivation for the choice of definition is given (and e.g. the definition of the primitive recursive functions is relegated to the exercises). Unusually for a textbook at this sort of level, the discussion of recursion theory in Ch. 8 goes far enough to cover a Gödelian ‘Dialectica’-style proof of the consistency of arithmetic, though the presentation is not particularly accessible.

Ch. 9 on set theory is perhaps the book’s real original raison d’être. It is a quarter of the whole text and was (if I recall right) the first extended textbook presentation of Cohen’s independence results via forcing, from four years previously. The treatment also touches on large cardinals. This was surely an admirable achievement in its time: but it is equally surely not now the place to start with set theory in general or forcing in particular, given the availability of later presentations.

Summary verdict Now only for very selective dipping into by already-well-informed (and perhaps rather masochistic) enthusiasts.

David Fray plays Bach

One of the most wonderful CDs of Bach keyboard music (indeed surely one of greatest Bach recordings ever) is Martha Argerich’s 1979 disc of the Partita No. 2, the Toccata BWV 911, and the English Suite No. 2. She plays with a quite extraordinary combination of clarity and sensitivity, of life and intensity. A hard act to follow.

Yet here in a new release is the young French pianist David Fray, also playing the Partita No. 2 and the same Toccata, but this time completing the disc (more generously) with the Partita No. 6. Surely the overlapping choice of programme here isn’t accidental. He is inviting a comparison. How does Fray’s disc  stand up?

I thought (and still think) that his recording of the Schubert Impromptus Op.90 and the Moments Musicaux is stunning (much better in this repertoire than the mannered Paul Lewis). I haven’t, though, heard his previous much admired Bach discs. But I’m now a new convert here too. This disc is surely remarkable. Fray has said  “We shouldn’t be afraid of acknowledging the expressiveness of Bach’s music”. And this is indeed expressive playing (yet within reason, without exaggeration), and again there’s great clarity and intensity. There is, for example, appropriate introspection in the 2nd Partita’s Sarabande and zest in the 6th Partita’s Air. This is overall a truly thoughtful and impressive recording. Warmly recommended.

Teach Yourself Logic, #9. The Big Books — Mendelson 1964

Continuing with a draft of the next section in the Big Books part of the Guide (see the previous post for more explanation):

Elliot Mendelson’s Introduction to Mathematical Logic (Van Nostrand, 1964: pp. 300) was first published in the distinguished and influential company of The University Series in Undergraduate Mathematics. It has been much used by generations of students since: a 4th edition was published by Chapman Hall in 1997 (pp. 440), with a slightly expanded 5th edition being published in 2009. I will here compare the first and fourth editions, as these are the ones I know.

This isn’t, in fact a very big Big Book: the length is kept under control in part by not covering a great deal, and in part by a certain brisk terseness. As the Series title suggests, the intended level of the book is upper undergraduate mathematics, and the book keeps to that aim. The style is indeed reasonably clear but though also now rather old-fashioned. (The choices of typography are not wonderfully pretty, and can make some pages look denser than they really are.)

After a brief introduction, Ch. 1 is on the propositional calculus. It covers semantics first (truth-tables, tautologies, adequate sets of connectives), then an axiomatic proof system. The treatments don’t change much between editions, and will only be of interest if you’ve never encountered a Hilbert-style axiomatic system before.

Ch. 2 is on quantification theory, again in an axiomatic style. The fourth edition adds to the end of the chapter more sections on model theory: there is a longish section on ultra-powers and non-standard analysis, then there’s (too brief) a nod to semantic trees, and finally a new discussion of quantification allowing empty domains. The extra sections in the fourth edition are a definite bonus: without them, there is nothing special to recommend this chapter, if you have worked through the suggestions in §1.1, and in particular the chapters in van Dalen’s book.

Ch. 3 is titled ‘Formal number theory’. It presents a formal version of first-order Peano Arithmetic, and shows you can prove some expected arithmetic theorems within it. Then Mendelson defines the primitive recursive and the (total) recursive functions, shows that these are representable (capturable) in PA. He then considers the arithmetization of syntax, and proves Gödel’s first incompleteness theorem and Rosser’s improvement. The chapter then proves Church’s Theorem about the decidability of arithmetic. One difference between editions is that the later proof of Gödel’s theorem goes via the Diagonalization Lemma; another is that there is added a brief treatment of Löb’s Theorem). If you’ve read my Gödel book or the equivalent, then there is nothing to divert you here, except that Mendelson does go through every single stage of laboriously showing that the relation m-numbers-a-PA-proof-of-the-sentence-numbered-n is primitive recursive.

Ch. 4 is on set theory, and — unusually for a textbook — the system presented is NBG (von Neumann/Bernays/Gödel) rather than ZF(C). In the first edition, this chapter is under fifty pages, and evidently the coverage can’t be very extensive and it also goes too rapidly. The revised edition doesn’t change the basic treatment (much) but adds sections comparing NBG to a number of other set theories. So while this chapter certainly can’t replace the introductions to set theory recommended in §1.7, it could be worth skimming briskly through the chapter in later editions to learn about NBG and other deviations from ZF.

The original Ch. 5 on effective computability starts with a discussion of Markov algorithms (again, unusual for a textbook), then treats Turing algorithms, then Herbrand-Gödel computability and proves the equivalence of the three approaches. There are discussions of recursive enumerability and of the Kleene-Mostowski hierarchy. And the chapter concludes with a short discussion of undecidable problems. In the later edition, the material is significantly rearranged, with Turing taking pride of place and other treatments of computability relegated to near the end of the chapter; also more is added on decision problems. Since the texts such as those by Cutland and Cooper mentioned in §1.6 don’t talk (much) about Markov or Herbrand-Gödel computability, you might want to dip into the chapter briefly to round out your education.

I should mention the appendices. The first edition has a very interesting appendix giving a version of Schütte’s variation on a Gentzen-style consistency proof for PA. Oddly this is missing from later editions. The fourth edition has instead an appendix on second-order logic.

Summary verdict There is now little reason to plough through the book end-to-end. It doesn’t have the charm and readability of Kleene 1952, and there are better separate introductions to each of the main topics. However, skim the early chapters if you’ve never seen axiomatic systems of logic used in earnest. Look at the section on non-standard analysis. If set theory is your thing, dip in to learn about NBG. And round out your knowledge of definitions of computation by looking through Ch. 5.

Teach Yourself Logic, #8. The Big Books — starting with Kleene 1952

OK, after a bit of a gap, it is back to thinking about the Teach Yourself Logic self-study Guide. The shape of the Guide is evolving as I write it (well, at least there is random mutation …). I’m now inclined to carve the material into three main chunks. Ch. 1 will still be more or less the existing chapter on ‘The basics’ (as in the current edition, Version 7.1 from November, available here). Ch. 3 will be the already-promised chapter ‘Exploring further’ (of which only one section is so far on-line). But now, sandwiched between those chapters, I’m planning a chapter surveying the ‘Big Books’ on mathematical logic.

The usual menu for a first serious mathematical logic course is another treatment of first-order logic, basic model theory, basic theory of computability and related matters (like the incompleteness theorems), and introductory set theory. So the plan in this new Ch.2 will be to look at some of the single or dual author multi-topic books  that aim to cover most or all of this menu, to give an indication of what they cover and — more importantly — how they cover it, while commenting on style, accessibility, etc.

It seems appropriate that this survey comes between Chs 1 and 3. For we will in fact be looking at further treatments of  material already covered in some of the sections of Ch.1,  keeping at the same or an only slightly more advanced level, without tackling some of the hairier excitements of Ch. 3.  The survey books rarely provide the best introductions now available to this or that area: but they can provide useful aids to widening and deepening understanding and can be revealing about how topics from different areas can fit together.

I don’t promise to discuss every worthwhile Big Book, or to give even coverage to those I do consider. But I’m again working on the principle that a patchy guide is better than none at all. I’m going to take the Big Books in chronological order, so here — to get things started — is my draft section on the first on the list. This indicates the level of detail that I’m thinking of doing things in. Comments welcome as usual.

First published sixty years ago, Stephen Cole Kleene’s Introduction to Metamathematics (North-Holland, 1962: pp. 550) for a while held the field as a survey treatment of first-order logic, the theory of computable functions, and Gödel’s incompleteness theorems.

In a 1991 note about writing the book, Kleene notes that up to 1985, about 17,500 copies of the English version of his text were sold, as were more thousands of various translations (including a sold-out first print run of 8000 of the Russian translation). So this is a book with a quite pivotal influence on the education of later logicians, and on their understanding of the fundamentals of recursive function theory and the incompleteness theorems in particular.

But it isn’t just nostalgia that makes old hands continue to recommend it. Kleene’s book remains particularly lucid and accessible: it is often discursive, pausing to explain the motivation behind formal ideas. It is still a pleasure to read (or at least, it ought to be a pleasure for anyone interested in logic enough to be reading this far into the Guide!).

Chs. 1–3 are introductory. There’s a little about enumerability and countability (Cantor’s Theorem); then a chapter on natural numbers, induction, and the axiomatic method; then a little tour of the paradoxes, and possible responses.

Chs. 4–7 are a gentle introduction to the propositional and predicate calculus and a formal system which is in fact first-order Peano Arithmetic (you need to be aware that the identity rules are treated as part of the arithmetic, not the logic). Although Kleene’s official system is Hilbert-style, he shows that ‘natural deduction’ introduction and elimination rules can be thought of as derived rules in his system, so it all quickly becomes quite user-friendly. (He doesn’t at this point prove the completeness theorem for his predicate logic: as I said, things go quite gently!)

Ch. 8 starts work on ‘Formal number theory’, showing that his formal arithmetic has nice properties, and then defines what it is for a formal predicate to capture (‘numeralwise represent’) a numerical relation. Kleene then proves Gödel’s incompleteness theorem, assuming a Lemma — eventually to be proved in his Chapter 10 — about the capturability of the relation ‘m numbers a proof [in Kleene's system] of the sentence with number n.

Ch. 9 gives an extended treatment of primitive recursive functions, and then Ch. 10 deals with the arithmetization of syntax, yielding the Lemma needed for the incompleteness theorem.

Chs. 11-13 then give a nice treatment of general (total) recursive functions, partial recursive functions, and Turing computability. This is all very attractively done.

The last two chapters, forming the last quarter of the book, go under the heading ‘Additional Topics’. In Ch. 14, after proving the completeness theorem for the predicate calculus without and then with identity, Kleene discusses the decision problem. And the final Ch. 15 discusses Gentzen systems, the normal form theorem, intuitionistic systems and Gentzen’s consistency proof for arithmetic.

Kleene writes beautiful clearly. And, modulo relatively superficial presentational matters, you’ll probably be struck by a sense of familiarity when reading through, as aspects of his discussions evidently shape many later textbooks (not least my own Gödel book). The Introduction to Metamathematics remains a really impressive achievement: and not one to be admired only from afar, either.

Summary verdict Still can be warmly recommended as an enjoyable and illuminating presentation of this fundamental material, written by someone who was himself so closely engaged in the early developments back in the glory days.

Ticking over quietly …

My short joint review of Volker Halbach’s and Leon Horsten’s not-now-so-recent books on truth (surprisingly published as a ‘Critical Notice’), which I’d already posted excerpts from here on the blog, is now online.

Things have been ticking over quietly since I sent off the book-I-promised-not-to-mention-again-until-the-dratted-thing-is-actually-published. But I have made a start in getting a page with sets of exercises under way. I envisage almost as many sets of exercises as there are chapters, which is a lot. And it is very slow work. For example, the very next set to be done, corresponding to the new Ch. 3 on the idea of effectively computable functions and effectively decidable sets, is planned to be almost a guided-teach-yourself-the-very-basics-of-computability-theory: and doing this sort of thing well is not easy. So I certainly don’t promise a full set of exercises by publication day. But — at least when interspersed with other things — it should be fun to slowly put them together.

I was in two minds about whether do include sets of answers alongside the question sets. But in fact, the time consuming part of all this is deciding on the exercises. And the utilitarian calculation is that there will be more students who will be pleased to have answers than there are instructors who will be displeased to have to think up a few more exercises of their own if/when they want class tests! So I will be providing answers.

In other news, just before Christmas Joseph Jedwab very kindly sent me a depressingly long list of corrections for the reprinted, supposedly corrected, version of Intro to Formal Logic. Sigh. You can download a list from the link on the book’s page here. (I hope the corrections can be made in physical copies when the book is next reprinted.)

What else? I’ve been distracted a little (one of the better things about being retired is that you have time for this sort of distraction) by reading one of those Great Books which has been on my shelves for years, but never properly read — on this occasion, it’s Saunders Mac Lane’s Mathematics: Form and Function. It’s a remarkable achievement. It’s not always easy to follow, so there was a bit of skipping. But there was the pleasure of being re-acquainted with some bits of maths that I last met doing tripos aeons ago. And more seriously, there was the pleasure and instruction of being reminded (or getting to see) How It All Hangs Together. If you think, as that Sellars quote has it, that philosophy is in the business of “seeing how things … hang together”, then this is a philosophical exploration (quite apart from Mac Lane’s occasional tanglings with explicitly philosophical claims about mathematics). I guess it should be compulsory reading for any philosopher interested in mathematics, and I’m rather regretting only having dipped in it before.

A suitable accompaniment to reading Mac Lane? My Christmas present to myself. Yes, yes, I agree: no one needs quite so many discs of that composer! Yet they are endlessly enjoyable if undemanding listening. Warmly recommended!

So that’s done then!

So …there it is. Or rather, there it was, a print-out of Gödel Mk 2 sitting on the table, before being taken off to the CUP building today, as an electronic version was emailed. Done and dusted. I hope. Of course I was agonizing over trivia up to the very last minute. But now I’ve promised myself not to look at it again till the presses are rolling and I can do no more about it. Nor will I mention it again here until near publication day. Promise! But, on the whole, that’s been a very enjoyable writing experience, and I’m very grateful to CUP for the chance of putting together a much improved version of the book.

Three cheers for TeXShop

As I write this, I’m printing out a hard copy of the Gödel book — hopefully the version to be taken along to CUP along with the PDF file when they re-open next week.

I’ve been tinkering with this second edition, on and off, since I got the contract back in July 2011 (and no doubt bored everyone who visits here by talking about it so much). It’s a long-ish book: 403 pages in all, with lots of symbols, lots of cross-references to resolve, not to mention auto generated bibliography and index. I’ve been using TeXShop + LaTeX (plus BibDesk) on a Mac. How many times did this document processing system crash, foul-up, or produce unintended gremlins over the eighteen months?

Zero. Yep, zero.

I’d say I was really impressed if it weren’t what I’ve come to take for granted. But it is pretty amazing now I stop to think about it. So it surely should occasionally still be said: Three cheers for LaTeX, for BibDesk, and not least to Richard Koch for TeXShop, my constant companion!

A Christmas card

All good wishes for a peaceful Christmas

In the dunce’s corner …

I’m spending a bit of quality time in the dunce’s corner, having dashed off a ‘solution’ to a problem in propositional calculus (yes propositional calculus, for heaven’s sake) over at math.stackexchange and got it quite wrong. And as fate would have it, I was off-line for a while, staying over with my aged mother, so couldn’t quickly delete it. Ho hum. So much for totting up “reputation points” eh?

OK: here’s the problem for you (from Enderton’s Math Logic book): let # be the three-place connective such that #(A, B, C) is true so long as the majority of A, B, C are true. Show that {#, ¬} is not an expressively adequate set of connectives.

Knowing I’m quite capable of that sort of thing makes the business of doing a final read of  Gödel 2 for thinkos a bit fraught. Even at this last minute stage I’ve found a silly omission. Ah well ….

Still, there are mistakes and mistakes. I had occasion a couple of days ago to look at James Robert Brown’s Philosophy of Mathematics where he makes a complete hash of understanding why the Intermediate Value Theorem is non-trivial (no, a diagram does not cut it). I was wondering about whether to bang on about that here, when — by one of those coincidences — I came across the ever-excellent T.W. Körner‘s Companion to Analysis where he takes a sideswipe at Brown: “The author cannot understand the problems involved in proving results like the intermediate value theorem and has written his book to share his lack of understanding with a wider audience.” Körner than proceeds to give a presentation which should be enough for most readers to work out (at least some of) what’s gone so wrong in Brown’s discussion. Job done.