Peter Smith's Blog, page 118

Proof reading again …

I’m slowly working through the proof-reader’s corrections for Gödel Mark 2 (and re-reading the book carefully one last time as I go). So far, I’ve got through a quarter of the book, and CUP’s reader has found two tiny slips (one a missing space I’d spotted myself, and the other a missing ‘that’ which is arguably optional anyway). OK, the reader also sprinkles around some suggestions for altering punctuation and italicization: but so far, I’m not inclined to make any of those further changes — taking the line that there is no special reason to depart from the conventions I adopted in the first edition which satisfied another proof reader.

So two tiny errors found in the first ninety-odd pages of my submitted PDF. Extremely good, I’d say. But no, it isn’t because I’m amazingly accurate at proof-reading my own work before sending it off. Au contraire. This is very much due to that experiment a few months ago in ‘crowd-sourcing’ the preliminary proof-reading for typos and thinkos. I can only say again how very grateful I am to everyone who helped out. The experiment obviously worked: I recommend it warmly to anyone else writing a similar book.

Weather report

“If you don’t like the weather in New England now, just wait a few minutes.” Mark Twain’s remark applies in spades in Old England. Changeable or what?

But one nice thing about retirement which they don’t tell you  – and I’m trying to look on the bright side here, you understand — is that the weather you experience really does get a whole lot better. For suddenly you have the freedom to snatch whatever nice half-days there are (and there are quite a few scattered about the average week, even this time of year) and you can get out for a walk in the winter sun. And when it is cold and dank and grey all day, you have the freedom to stick at home in the warm, Reading a Good Book or whatever.

Not that my timetable used to be so very constraining, to be honest. But after a few decades you do rather get into a fixed mindset: Thursdays are work days and so it must be nose to the grindstone.

Not now: these days, it is positively Liberty Hall.  Nice morning? Then the proof-correcting can wait. Bitter afternoon (as it is now)? Then it is tea and cake and Haydn and the red pen …

Make mine an Earl Grey.

The Decline of the West, Episode 42

Here’s a very dispiriting new blog post by Tim Gowers about the dire state of school maths teaching in the UK. I’m a bit surprised, though, that he’s surprised by what he discovered. Certainly, my experience teaching Cambridge philosophy students (a very bright lot), about half of whom had done A-level maths and got top grades, was that very few of them really understood any maths. They might have picked up a bag of tricks to apply in response to some formulaic questions. But as for some conceptual understanding of classical analysis or an appreciation of the idea of rigorous proof ‘in the wild’ … Sigh. (No wonder philosophy of mathematics can leave them cold!)

And judging from the many comments to Tim Gowers’s post, the decline in school maths teaching is not confined to this declining off-shore island.

Well, there’s no point in moaning about this, though I hope my local friendly mathematicians are exercising what influences they can to help stop the rot. But it does mean that there’s a real problem for teachers of logic and writers of logic books aimed at students. We tend to be mathematically ept ourselves, and students are good at dissembling — or at least, at remaining silent — so we can so easily fail to realize just how mathematically inept so many of our students are (through no fault of theirs, let it be emphasized). What to do? I don’t have the teaching problem any more: but I do have the writing problem. I guess I’ve fallen over the years into working with the principle if in doubt, go slower and explain even more. But it does make for long books to write and long books to read.

 

Teach Yourself Logic, #7. A bit of deviance

There’s a new version of the self-help Guide downloadable from the Teach Yourself Logic page. Heavens this is time consuming, but having (as it now seems, foolishly) started, I guess I should do the best job on this that I can. Anyway, there are new sections on extensions of classical logic (second order, plural, free) and deviations from the classical paradigm (intuitionism, relevance logics). There also is a major structural change to the Guide. It is now going to be in two big chapters, one on the basics and one on more advanced stuff. Partly this is to make it all look less daunting (the idea is that any grad student working in logic-relevant areas ought to know the sort of stuff that is in Ch. 1, and then the enthusiasts for this or that area can pursue the relevant sections of Ch. 2). And partly this is to acknowledge the fact more advanced work in one area can often presuppose familiarity the basics in other areas.

All suggestions for improvement welcome as always. I’d welcome in particular any additional introductory suggestions on Second-Order Logic, and on Intuitionistic Logic. At the moment, on Second-Order Logic, I start by mentioning the article

Herbert Enderton, ‘Second-order and Higher-order Logic’, Stanford Encyclopedia of Philosophy. http://plato.stanford.edu/entries/log...

And suggest following that up with

John L. Bell, David DeVidi and Graham Solomon’s Logical Options: An Introduction to Classical and Alternative Logics (Broadview Press 2001), §3.3.

But now what? Stewart Shapiro, Foundations without Foundationalism: A Case for Second-Order Logic, Oxford Logic Guides 17 (Clarendon Press, 1991) is very accessible — but is there something less weighty to read beforehand?

And on Intuitionist Logic, I suggest starting with

John L. Bell, David DeVidi and Graham Solomon’s Logical Options §§5.2, 5.3., which give an elementary explanation of the contructivist motivation for intuitionist logic, and then explains a tree-based proof system for both propositional and predicate logic.
Graham Priest, An Introduction to Non-Classical Logic (CUP, much expanded 2nd edition 2008), Chs. 6, 20. These chapters of course flow on naturally from Priest’s treatment in that book of modal logics, first propositional and then pred icate.
Then, up a notch in mathematical sophistication (but manageable if you have tackled earlier chapters in this book, so you are familiar with the style), there is Dirk van Dalen, Logic and Structure (Springer, 4th edition 2004), §§5.1–5.3.

We will return in Ch. 2 to some further explorations of intuitionism where we’ll mention e.g. Dummett’s book. But what about other more introductory level material?

 

Postcard from Turin

It’s been a while since we were in Italy, so a quick city break — this time to Turin (a new city for us). The central city is rather impressive, wide colonnaded streets and some large piazzas. And with the streets being laid on pretty much on a grid system, you get some very long urban views, with occasional glimpses of the mountains beyond. We (unsurprisingly) had some pretty good meals, and paused not a few times in cafés — for the best ever macchiato, go to the delightful Caffe Mulassano. But the high point of our visit was (surprisingly) the Museo Egizio. Yes, of course this is famous, usually said to be the best Egyptian museum outside Cairo: but to be honest we went a bit dutifully, only to be bowled over. The collection really is quite overwhelming. The museum is undergoing refurbishment, and a  lot of the exhibits are still shown in a very old fashioned way, but even so, the cumulative effect especially of all the small ancient grave goods is astonishing. And the theatrically lit new display of the monumental statues is exceedingly dramatic. Surely unmissable if you happen to find yourself in Turin.

Teach Yourself Logic, #6

A new page for the Guide is now here on the site. And a new version of the Guide (Version 6.0, 6th November) can be downloaded from there. It goes without saying, of course, that all constructive comments and suggestions will be welcome.

Teach yourself logic, #5: Arithmetic, computation and Gödelian incompleteness

I’ve just written a (partial) draft of another chunk of my developing Teach Yourself Logic reading guide. As always, comments and suggestions will be very welcome indeed. I’ve tried to restrain myself, but this segment of the Guide is already rather long. But here goes …

A standard part of any logician’s education will be an encounter with first-order Peano Arithmetic as a non-trivial example of a rigorously formulated axiomatic system, and with Gödel’s epoch-making proof of the incompleteness of PA, and indeed of any nice enough theory that can ‘do’ enough arithmetic.

Gödel’s 1931 proof uses facts about primitive recursive functions (a subclass of the computable functions), and you certainly need to know about them. A more general treatment of the idea of an effectively computable function (arguably capturing all of them) was developed a few years later, is of the greatest intrinsic interest and also throws more light on the incompleteness phenomenon. So there’s a choice to be made. Do we look at things in a roughly historical order, proving initial versions of Gödel’s incompleteness theorem before moving on to look at the general treatment of computable functions. Or do we do some of the general theory first? Here are two books to start with which take the two different routes:

Peter Smith, An Introduction to Gödel’s Theorems (CUP 2007) does things in the historical order. Don’t be put off by the series title ‘Cambridge Introductions to Philosophy’: putting it in that series was the price I paid for cheap paperback publication. This is still quite a meaty logic book, with a lot of theorems and a lot of proofs, but I hope rendered very accessible.
Richard Epstein and Walter Carnielli, Computability: Computable Functions, Logic, and the Foundations of Mathematics (Wadsworth 2nd edn. 2000) does computability theory first. This is a nicely introductory book, clearly done, with lots of interesting historical information too in Epstein’s 28 page timeline on ‘Computability and Undecidability’ at the end of the book.

As you’ll already see from these two books, this is a delightful area. Elementary computability theory is conceptually very neat and natural, and the early Big Results are proved in quite remarkably straightforward ways (just get the hang of the basic ‘diagonalization’ construction, the idea of Gödel-style coding, and one or two other tricks and off you go …).

A notch up in difficulty, here’s another book that focuses on the general theory of computation:

George Boolos, John Burgess, Richard Jeffrey, Computability and Logic (CUP 5th edn. 2007). This is the latest edition of an absolute classic. The first version (just by Boolos and Jeffrey) was published in 1974; and there’s in fact a great deal to be said for the 1990 third edition as being the best. The later versions have been done by Burgess and have perhaps lost elegance and some of the individuality, and the level of difficulty has become uneven. But this is still great stuff, and you will want to read the first two parts of the book at an early stage, perhaps being more selective when it comes to the last part, ‘Further Topics’.

An interestingly unusual route to the incompleteness phenomenon is traced in

Melvin Fitting, Incompleteness in the Land of Sets (College Publications, 2007). Short, also fairly elementary, elegant and very clear.

After these, where should you go? Here are three stand-out suggestions:

Nigel Cutland, Computability: An Introduction to Recursive Function Theory (CUP 1980). This is a rightly much-reprinted classic and is beautifully put together. It does have the look-and-feel of a maths text book. But if you can cope with Boolos and Jeffrey, you can manage this.
Raymond Smullyan, Godel’s Incompleteness Theorems (Oxford Logic Guides, OUP, 1992) is another modern classic. Terse and elegant, proving some beautiful slightly abstract versions of the incompleteness theorems.
Richard Kaye, Models of Peano Arithmetic (Oxford Logic Guides, OUP, 1991) is a third classic, connecting up the treatment of arithmetic with material on model theory, and telling us a great deal about non-standard models of PA (models which contain more than the ‘real’ natural numbers). And this reveals more about what PA can and can’t prove — though be warned that this book is rather more challenging in places.

That is probably more than enough about the logical basics. The literature on computability is huge, however, and I haven’t yet mentioned any books that approach things from a computer-science rather than a pure-logic perspective, and deal inter alia with the fascinating topic of computational complexity. So I had better touch on a few of those. But first, here’s an aside mentioning a few more books with a logical flavour, at very varied levels:

[At this point, in small print, I go on to mention (with shorter comments)

Rósza Péter, Recursive Functions  (1967).
Hartley Rogers, Jr., Theory of Recursive Functions and Effective Computability (1967)
Herbert B. Enderton, 'Elements of Recursion Theory', in J. Barwise, ed., Handbook of Mathematical Logic (1977).
Piergiorgio Odifreddi, Classical Recursion Theory , Vol. 1 (1989)
Martin Goldstern and Haim Judah, The Incompleteness Phenomenon (1998).
A. Shen and N. K. Vereshchagin, Computable Functions (2003).
Per Lindström, Aspects of Incompleteness (2003). Terse, not always reader-friendly, but well repays the effort.
Torkel Franzén, Inexaustibility (2004).
S. Barry Cooper, Computability Theory (2004).

which all have virtues of various kinds!]

As I mentioned, computer scientists are — surprise, surprise! — interested in the theory of computation, and their books tend to have a different slant. It is certainly worth knowing at least a little about the topic of computational complexity. I’ll mention just three places to start:

Michael Sipser, Introduction to the Theory of Computation (Thomson, 2nd edn. 2006) is a standard and very well regarded text. It aims to be very accessible and to take its time giving clear explanations of key concepts and proof ideas. I think it is successful. The last third of the book is on computational complexity.
Ofed Goldreich, P, NP, and NP-Completeness (CUP, 2010). Short, clear, and introductory stand-alone treatment of computational complexity.
Ashley Montanaro, Computational Complexity , notes for a 2012 lecture course here in Cambridge. This has a useful quick guide to further reading, so I don’t need to add anything further here.

And that’s surely more than enough! But any suggestions for additions? deletions? improvements? 

Gaps in the truth about truth according to Leon Horsten?

I very much like Leon Horsten’s The Tarskian Turn as an attempt to make more widely available some recent work on formal axiomatic theories of truth,  without scaring readers off by excessive technicality or by unnecessarily spelling out tricky proofs. Students doing an advanced course on the notion of truth really ought to know the headlines about this  formal stuff, for a reason Tim Williamson has stressed:

One clear lesson [of these logical investigations] is that claims about truth need to be formulated with extreme precision, not out of kneejerk pedantry but because in practice correct general claims about truth often turn out to differ so subtly from provably incorrect claims that arguing in impressionistic terms is a hopelessly unreliable method.

So three cheers for Horsten’s efforts at lucid and lively explanation here. But his book is more than a merely expository essay. It is philosophically opinionated, takes sides, and even is prepared to endorse one particular axiomatic theory of truth as philosophically in good shape. This makes The Tarskian Turn engagingly provocative.

As is common in these sorts of investigations, Horsten takes as a test case the enterprise of adding a theory of truth to first-order Peano Arithmetc, PA. And the theory he recommends is PKF (that’s Feferman’s axiomatization of Kripke’s three-valued model, but redone in a Partial, gappy, logic). Roughly the idea is that you augment the language of PA with a truth-predicate T, take a rule version of Kleene’s strong logic, add the non-induction axioms of PA and the rule form of induction. 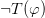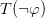Then we have the T-biconditionals of atomic sentences of PA, plus two-way rules that allow us to commute T with the logical operators: so, in Horsten’s sloppy but readable shorthand, we can infer from  and vice versa, and similarly for other operators. 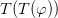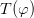Finally we have a two-way rule that allows us to infer  from  and vice versa.

The T-rules here are entirely natural, so PKF has all kinds of nice features. In particular, it is easily seen that everything remains classical for T-free sentences, and so classical PA can proceed undisturbed. So it is only some sentences involving T for which PKF’s non-classicality really matters and where e.g. excluded middle fails (where indeed we might want it to fail). Horsten thinks PKF is a best buy. Is it?

In his much more expansive, much more technically detailed book Axiomatic Theories of Truth Volker Halbach also investigates  PKF but is much less enthusiastic about it. Partly this is because of a general resistance to the idea of departing from classical logic if that can be avoided. And partly this is because of technical observations about the mathematical limitations of PKF (it can’t do much transfinite induction on open wffs involving the T-predicate). However, I don’t see why Horsten need be moved by these considerations. After all, logical regimentation always involves trade-offs of costs and benefits: and Horsten will say that given pure arithmetic remains classical, the cost of having to go non-classical in ones background logic (in ways that only really matter in cases that involve troublesome uses of the T-predicate) is a price worth paying for the benefit of skirting round paradox. And if that leads us to restrict transfinite induction in cases of no ordinary mathematical interest, why care?

But there are other worries about PKF. As Horsten notes, it isn’t that PKF rejects excluded middle in the troublesome cases, but rather it is silent. But is silence really what we want from a theory here? Horsten cheerfully says

The system PKF … is not vulnerable to a strengthened liar attack because it makes no claim concerning the truth value of the liar sentence. PKF simply does not assert the liar sentence, nor its negation, nor that it is true, nor that it is not true.

Indeed. But now the theory is out there, on the table for all to see, can’t we as philosophers stand back and reflect on it, and forcefully raise the question of the truth or otherwise of claims on which PKF fails to give a verdict? And off we go again … (To be sure there are philosophical positions where refusal to affirm or deny a putative proposition P is backed up with therapy that is supposed to massage away our temptation to suppose that P does express a contentful proposition. But Horsten is the business of theory not therapy.)

Horsten himself, then, is remarkably silent on what seems to be an obvious question. Instead he concludes his book by considering whether PKF is at least consonant with a broadly deflationist or minimalist stance. He thinks it is. For the theory treats truth as an insubstantial property without ‘a fixed nature or essence’ in the sense that there is no more to truth than is grasped in grasping some inference rules (though Horsten in fact  doesn’t rule out there being inference rules beyond those codified in PKF). But what about the fact that the compositional theory is non-conservative over arithmetic? Indeed PKF is arithmetically as strong as a transfinitely ramified system of predicative analysis that goes by the label , whose first-order arithmetical consequences go far beyond those of PA.

Horsten is remarkably unworried. I think he is too swayed by a (quoted) claim of Feferman’s that suggests that systems of predicative analysis only elaborate commitments that are already implicit in accepting PA, a suggestion that runs clean against Isaacson’s well-known thesis (which I’ve defended elsewhere) that PA marks the natural boundary of those truths that can be reached by purely arithmetical reasoning. We can’t examine who is right about that here. But we might complain that neither does Horsten: he fails to acknowledge just how contentious it is to suppose that the progression through systems of predicative analysis stronger than the arithmetically conservative system 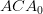can somehow be regarded as insubstantial rather than as involving new infinitary ideas (and so it remains equally contentious to suppose that a theory of truth arithmetically equivalent to a strong system of analysis can still count as deflationary). We might well dissent at the end of the book, then, about Horsten’s philosophical assessment of the merits of PKF.

Still, I think we should still be very grateful for a beautifully structured guided tour, with thought-provoking commentary, making some recent formal work on truth accessible to a wide student audience interested in the truth about truth (and accessible as well as to non-expert colleagues who want to know what the logicians down the corridor have been up to).

The consistency of NF

Randall Holmes has now announced “I believe that I am in possession of a fairly accurate outline of a proof of the consistency of New Foundations.”

He goes on to say “NF has the same consistency strength as TST + Infinity, has the same kinds of extensions as NFU in the same ways, has no interesting consequences for the combinatorics of small sets, etc. No surprises, this is a rather boring outcome in my opinion …” Well, I don’t know about boring! If Randall has indeed cracked this long-standing problem, it’s a major achievement. He is still editing the document, so nothing is released yet. However, Thomas Forster is organizing a conference here in Cambridge in the spring and Randall says he will “certainly be discussing this.”

And Thomas confirms  ”I am indeed organising an NF meeting in Cambridge in the spring, current intention is last week of March and first week of April. The idea is that before Randall arrives there will be a warm-up act wherein the background and some preparatory material is set out for people who are not already familiar with it. Thus when Randall arrives we will all be primed and ready to go. … I am not at this stage soliciting other offers of talks, tho’ that may change. If you have something you think I may find irresistible by all means try to twist my arm. And – of course – contact me if you want to come.”

February 2013 concerts: Takacs and Pavel Haas Quartets

Just so you can’t complain if I later post rave reviews of concerts you didn’t know about …  The Takacs Quartet are going to be in Cambridge playing in the very intimate small Peterhouse theatre on February 23rd in the Camerata Musica season (the Hagen Quartet and András Schiff are also playing in the season early next year: which would be a quite astonishing line-up were it not for the fact that previous seasons have been equally stellar). And the Pavel Haas Quartet, whom I have enthused about here before, are playing at the Wigmore Hall on February 26 including the Beethoven Op. 130 with the Grosse Fuge. There are tickets left for both concerts as I post (but not for long, I imagine).