Peter Smith's Blog, page 112
November 18, 2013
The Škampa Quartet play Mozart and Smetena
We’d booked to see the Pavel Haas Quartet play at lunchtime at the Wigmore Hall today, but they have had to delay restarting their concert schedule, and so we heard the Škampa Quartet as their truly excellent stand-ins. They played Mozart’s Quartet in D, K575 with considerable finesse and charm and persuasiveness. But what made the concert was a performance of the first of Smetena’s quartets, ‘From my life’. Passionate, intimate, dancing and lyrical by turn, the Škampa played with true heart and soul (and wonderful togetherness). This was a very fine performance indeed. We heard the Pavel Haas play the Smetena last year, and that was perhaps even more remarkable an experience: but the Škampa in their current line-up were definitely more than worth the day trip to London to hear.
I’m mentioning this because you can hear the concert for the next week on BBC Radio 3, here.
November 15, 2013
TYL, #18: another update for the Teach Yourself Logic Guide
After a bit of a hiatus, there’s now another update for the Teach Yourself Logic Guide. So here is Version 9.3 of the Guide (pp. iii + 68). Once more, do spread the word to anyone you think might have use for it.
And by the way, there’s a stable URL for the page which always links to the latest version, http://logicmatters.net/students/tyl/, which you can use in reading lists, or on your website’s resources page for graduate students, etc.
The main new addition is a two-page overview of Peter Hinman’s blockbuster, Fundamentals of Mathematical Logic. But there are a couple of other additional reviews in the Big Books appendix, and as always there has also been some minor tinkering throughout.
The previous version from 1 September has been downloaded over 2500 times in ten weeks. As I’ve said before, I’m therefore encouraged to occasionally continue revising and expanding as people seem to be finding the Guide useful. So keep watching this space …
November 14, 2013
Gödel’s incompleteness theorems, on SEP at last
The Stanford Encyclopedia of Philosophy (what would we do without it?) has at last filled one of its notable gaps in coverage: there is now a entry by Panu Raatikainen on Gödel’s Incompleteness Theorems. It isn’t quite how I would have written such an entry, but it is clear and very sensible, and certainly won’t lead the youth too badly astray (which needs to be said when it comes to discussions of these things!).
Here, though, are a few comments. I start with three places where the discussion could perhaps mislead:
(1) There’s an early section on ‘The Relevance of the Church-Turing Thesis’, which starts
Gödel originally only established the incompleteness of a particular though very comprehensive formalized theory P, a variant of Russell’s type-theoretical system … it was, at the time, unclear just how general [his result] really was … What was still missing was an analysis of the intuitive notion of decidability, needed in the characterization of the notion of an arbitrary formal system.
This rather suggests that we only get a clean general result round about 1936 when we have homed in on a sharp general account of effective decidability. But of course, Gödel’s original paper already gives a perfectly sharp general formulation: if the axioms and rules of inference of a theory T are primitive-recursively definable, and T represents every primitive recursive relation, then T is incomplete so long as omega-consistent (and indeed there will be arithmetical sentences undecidable by T). Moreover, the restriction here to primitively-recursively axiomatized systems is no real restriction. And I’m not thinking here of the technical point that any recursively axiomatized theory can be primitive-recursively re-axiomatized; there’s a more humdrum point — any effectively axiomatized system you are likely to dream up will already be primitive-recursively axiomatized (unless we are trying to be perverse, we don’t ordinarily define a class of axioms, for example, in such a way that it will require an open-ended search to determine whether a given sentence belongs to the class). So: I think it would be better to say that Gödel 1931 already gives a beautifully general result. And the fact that we can extend it from the primitively-recursively axiomatized to recursively axiomatized theories is pretty much a technical footnote.
(2) In the section describing how the First Theorem might be proved, we read
The next and perhaps somewhat surprising ingredient of Gödel’s proof is the following important lemma … The Diagonalization Lemma
Let A(x) be an arbitrary formula of the language of F with only one free variable. Then a sentence D can be mechanically constructed such that
F ⊢ D ↔ A(⌈D⌉).
Well, not Gödel’s proof. As in fact Raatikainen himself notes later.
As to the Diagonalization Lemma, actually Gödel himself originally demonstrated only a special case of it, that is, only for the provability predicate. The general lemma was apparently first discovered by Carnap 1934.
But that’s still wrong on both counts. Gödel didn’t state even the restricted version in 1931, nor in his 1934 lectures. Nor does Carnap’s 1934 Logische Syntax der Sprache.
We need to distinguish two different claims, which we might call the Diagonal Equivalence and the Diagonal Lemma. The Lemma we have just met, and is a syntactic claim about what can be proved. The Equivalence is a semantic claim, to the effect that given an arbitrary formula A(x) we can construct as sentence D such that D is true on interpretation just in case A(⌈D⌉) is. And it is this semantic Equivalence claim that Gödel refers to in his 1934 lectures.
Now, in §35 of his 1934, Carnap neatly proves the general Diagonal Equivalence, and in §36 he uses this, together with the assumption that not provable is expressible by an open wff in his Language II to show that Language II is incomplete. But note that constructing the semantic Diagonal Equivalence is not to establish the Diagonalization Lemma. And Carnap doesn’t actually state or prove that in his §35. And when we turn to §36, we see that Carnap’s argument for incompleteness is the simple semantic argument depending on the assumed soundness of his Language II. So at this point Carnap is giving a version of the semantic incompleteness argument sketched in the opening section of Gödel 1931 (the one that appeals to a soundness assumption), and not a version of Gödel’s official syntactic incompleteness argument which appeals to omega-consistency. Indeed, Carnap doesn’t even mention omega–consistency in the context of his §36 incompleteness proof. He doesn’t need to.
Anyway, neither Gödel 1931 or 1934 nor Carnap 1934 state the modern syntactic Diagonalization Lemma (as opposed to the semantic Equivalence). And I’m not sure who first did.
(3) We’ve just touched on the point that Gödel 1931 has two proofs that there are undecidable sentences in sufficiently rich theories, the first one depending on the semantic assumption that the theory is sound (and the weak assumption that it can express primitive recursive relations), the other depending on the syntactic assumption that the theory is omega-consistent (and the stronger assumption that it can represent p.r. relations). Students ought to know this, or they will get confused when they read some other discussions.
Well, Raatikainen does bury some relevant remarks at the end of his piece. He speaks of
a weak version of the incompleteness result: the set of sentences provable in arithmetic can be defined in the language of arithmetic, but the set of true arithmetical sentences cannot; therefore the two cannot coincide. Moreover, under the assumption that all provable sentences are true, it follows that there must be true sentences which are not provable. This approach, though, does not exhibit any particular such sentence.
But this perhaps forgets that Gödel’s own initial semantic argument (p. 149 in Collected Papers Vol. I) does of course exhibit a particular undecidable sentence.
A couple more observations. First, I thought section on ‘Feferman’s Alternative Approach to the Second Theorem’ was probably too compressed to be very useful. Second, it is natural to ask: are there ‘ordinary’ arithmetical statements which (like Gödel sentences) we can frame in the language of PA, which are also unprovable in PA, though we can prove them true using richer resources? The section on ‘Concrete Cases of Unprovable Statements’ addresses this, briefly, but then moves on to talking about unprovable statements in richer languages, unprovable in richer theories. Students might be puzzled about whether there is supposed to be any unity to these examples and what, if anything, they are supposed to show which they haven’t learnt from Gödel’s theorems.
But all that said, it is excellent to see the SEP filling an obvious gap with an accessible and (mostly) very clear discussion!
November 1, 2013
Does mathematics need a philosophy? — 3
Some final thoughts after the TMS meeting last week (again, mostly intended for local mathmos rather than the usual philosophical readers of this blog …).
Consider again that rather unclear question ‘Does mathematics need a philosophy?’. Here’s another way of construing it:
Are mathematicians inevitably guided by some general conception of their enterprise — by some ‘philosophy’, if you like — which determines how they think mathematics should be pursued, and e.g. determines which modes of argument they accept as legitimate?
Both Imre Leader and Thomas Forster touched on this version of the question in very general terms. But to help us to think about it some more, I suggest it is illuminating to have a bit of detail and revisit a genuine historical debate.
We need a bit of jargon first (which comes from Bertrand Russell). A definition is said to be impredicative if it defines an object E by means of a quantification over a domain of entities which includes E itself. An example: the standard definition of the infimum of a set X is impredicative. For we say that y = inf(X) if and only if y is a lower bound for X, and for any lower bound z of X, z ≤ y. And note that this definition quantifies over the lower bounds of X, one of which is the infimum itself (assuming there is one).
Now Poincaré, for example, and Bertrand Russell following him, famously thought that impredicative definitions are actually as bad as more straightforwardly circular definitions. Such definitions, they suppose, offend against a principle banning viciously circular definitions. But are they right? Or are impredicative definitions harmless?
Well, local hero Frank Ramsey (and Kurt Gödel after him) equally famously noted that some impredicative definitions are surely entirely unproblematic. Ramsey’s example: picking out someone as the tallest man in the room (the person such that no one in the room is taller) is picking him out by means of a quantification over the people in the room who include that very man, the tallest man. And where on earth is the harm in that? Surely, there’s no harm at all! In this case, the men in the room are there anyway, independently of our picking any one of them out. So what’s to stop us identifying one of them by appealing to his special status in the plurality of them? There is nothing logically or ontologically weird or scary going on.
Likewise, it would seem, in other contexts where we take a realist stance, and where we suppose that – in some sense – reality already supplies us with a fixed totality of the entities to quantify over. If the entities in question are ‘there anyway’, what harm can there be in picking out one of them by using a description that quantifies over some domain which includes that very thing?
Things are otherwise, however, if we are dealing with some domain with respect to which we take a less realist attitude. For example, there’s a line of thought which runs through Poincaré, an early segment of Russell, the French analysts such as Borel, Baire, and Lebesgue, and then is particularly developed by Weyl in his Das Kontinuum: the thought is that mathematics should concern itself only with objects which can be defined. [This connects with something Thomas Forster said, when he rightly highlighted the distinctively modern conception of a function as any old pairing of inputs and outputs, whether we can define it or not -- this is the ‘abstract nonsense’, as Thomas called it, that the tradition from Poincaré to Weyl and onwards was standing out against.] In that tradition, to quote the later great constructivist mathematician Errett Bishop,
A set [for example] is not an entity which has an ideal existence. A set exists only when it has been defined.
On this line of thought, defining a set is – so to speak – defining it into existence. And
from this point of view, impredicative definitions will indeed be problematic. For the definitist thought suggests a hierarchical picture. We define some things; we can then define more things in terms of those; and then define more things in terms of those; keep on going on. But what we can’t do is define something into existence by impredicatively invoking a whole domain of things already including the very thing we are trying to define into existence. That indeed would be going round in a vicious circle.
So the initial headline thought is this. If you are full-bloodedly realist — ‘Platonist’ — about some domain, if you think the entities in it are ‘there anyway’, then you’ll take it that impredicative definitions over that domain can be just fine. If you are some stripe of anti-realist or constructivist, you will probably have to see impredicative definitions as illegitimate.
Here then, we have a nice example where your philosophical Big Picture take on mathematics (‘We are exploring an abstract realm which is “there anyway”’ vs. ‘We are together constructing a mathematical universe’) does seem to make a difference to what mathematical devices you can, on reflection, take yourself legitimately to use. Hence the fact that standard mathematics is up to its eyes in impredicative constructions rather suggests that, like it or not, it is committed to a kind of realist conception of what it is up to. So yes, it seems that most mathematicians are implicitly caught up in some general realist conception of their enterprise, as Imre and Thomas in different ways came close to suggesting. In the terms of the previous instalment, we can’t, after all, so easily escape entangling with some of the Big Picture issues by saying ‘not our problem’.
Return to the story I gestured at in the last instalment about what I called the the Battle of the Isms. I rather cheated by then assuming that the game was taking mathematics uncritically as it is and seeing how it fits in the rest of our story of the world and of our cognitive grasp of the world. In other words, I took it for granted that the enterprise of trying to get an overview, trying to understand how mathematics fits together with other forms of enquiry, isn’t going to produce some nasty surprises and reveal that the mathematicians might somehow have being doing some of it wrong, and need to mend their ways! But as we’ve just been noting, historically that isn’t how it was at all. So while Logicism (which Imre mentioned) and Hilbert’s sophisticated version of Formalism were conservative Isms, which were supposed to give us ways of holding on to the idea that — despite its very peculiar status — classical mathematics is just fine as it is, these positions were up against some radically critical strands of thought. These included famously Brouwer’s Intutionism as well as Weyl’s Predicativism. The critics argued that the classical maths of the late nineteenth century had over-reached itself in descending into ‘abstract nonsense’ (which was why we got a crisis in foundations when the set-theoretic and other paradoxes were discovered), and to get out of the mess we need to stick to more constructivist/predicativist styles of reasoning, recognising that world of mathematics is in some sense our construction (which you might think has something to do with how we can get to know about it).
Now, that’s more than a little crude and we can’t follow those debates any further here. As a thumbnail history, though, what happened is that as far as mathematical practice is concerned the conservative classical realists won. Predicative analysis, for example, survives in a small back room of the mansion of mathematics, where its practitioners still like to show off how you far you can get hopping on one leg, with an arm tied behind your back — as the lovers of abstract nonsense, as Thomas described himself, might put it. Though by the way, it very importantly turns out that predicative analysis is all that science actually needs (so we don’t have, so to speak, external, practical reasons for going classical). But the victory of the classical realists wasn’t a conceptually well-motivated philosophical victory — there are such things, sometimes, but this certainly wasn’t one of them. The conceptual debates spluttered on and on, but the magisterial authority of Hilbert and others was enough to convince most mathematicians that they needn’t change their way of doing things. So they didn’t.
Yet it seems that we can imagine things having gone differently on some Twin Earth, where the internal culture (the philosophy, if you like) of mathematicians developed differently over a hundred years, so that low-commitment approaches were particularly prized, and the constructivists/predicativists got to occupy the main rooms of the mansion, dishing out the grants to their students, while the lovers of abstract nonsense were banished to the attics to play with their wild universe of sets in the Department of Recreational Mathematics. Or if we can’t imagine that, why not?
There’s a lot more to be said. But maybe, just maybe, it does behove mathematicians — before they scorn the philosophers — to reflect occasionally that it really isn’t quite so obvious that our mathematical practice is free from deep underlying philosophical presumptions (even in a broad, Big Picture sense).
October 31, 2013
Does mathematics need a philosophy? — 2
A few more thoughts after the TMS meeting (mainly for non-philosophers) …
‘Does mathematics need a philosophy?’ The question isn’t exactly transparent. So, to ask one of those really, really annoying questions which philosophers like to ask, what exactly does it mean?
Well, here’s one more focused question it could mean (and it was in part taken to mean in the TMS discussion): should mathematicians take note of, care about, the philosophy of mathematics as currently typically done by paid-up philosophers of mathematics? Both Imre Leader and Thomas Forster had something to say about this. And they agreed. The answer to this more focused question, they said, is basically “no”. Thomas went as far as saying,
The entirety of “Philosophy of Mathematics” as practised in philosophy departments is — to a first approximation — a waste of time, at least from the point of view of the working mathematician.
Fighting talk, eh?! But is that a reasonable assessment?
Well, I suppose it could have been that much of the philosophy is a waste of time because philosophers just don’t know what the heck they are talking about when it comes to mathematics. But that’s rather unlikely given how many professional philosophers have maths degrees (when I was in the Philosophy Faculty, a third of us had maths degrees, including one with a PhD and another with Part III under their belts). So it probably isn’t going to be just a matter of brute ignorance. What’s going on among the philosophers, then, that enables Imre and Thomas to be quite so sniffy about the philosophy of mathematics as practised?
Here’s my best shot at a charitable reading of their shared view. There’s a lovely quote from the great philosopher Wilfrid Sellars that many modern philosophers in the Anglo-American tradition [apologies to those Down Under and in Scandinavia ...] would also take as their motto:
The aim of philosophy, abstractly formulated, is to understand how things in the broadest possible sense of the term hang together in the broadest possible sense of the term.
Concerning mathematics, then, we might wonder: how do the abstract entities that maths seems to talk about fit into our predominantly naturalistic world view (in which empirical science, in the end, gets to call the shots about what is real and what is not)? How do we get to know about these supposed abstract entities (gathering knowledge seems normally to involve some sort of causal interactions with the things we are trying to find out about, but we can’t get a causal grip on the abstract entities of mathematics)? Hmmmm: what maths is about and how we get to know about it — or if you prefer than in Greek, the ontology and epistemology of maths — seems very puzzlingly disconnected from the world, and from our cognitive capacities in getting a grip on the world, as revealed by our best going science. And yet, … And yet maths is intrinsically bound up with, seems to be positively indispensable to, our best going science. That’s odd! How is it that enquiry into the abstract realms of mathematics gets to be so empirically damned useful? A puzzle that prompted the physicist Eugene Wigner to write a famous paper called “The Unreasonable Effectiveness of Mathematics in the Natural Sciences”.
Well, perhaps it’s the very idea of mathematics describing an abstract realm sharply marked off from the rest of the universe — roughly, Platonism — that gets us into trouble. But in that case, what else is mathematics about? Structures in some sense (where structures can be exemplified in the non-mathematical world too, which is how maths gets applied)? — so, ahah!, maybe we should go for some kind of Structuralism about maths? But then, on second thoughts, what are structures if not very abstract entities, after all? Hmmmm. Maybe mathematics is really best thought of as not being about anything “out there” at all, and we should go for some kind of sophisticated version of Formalism after all?
And so we get swept away into esoteric philosophical fights, as the big Isms slug it out (there are more guys than I’ve mentioned waiting on the sidelines to join in too: I’ll come back to them in the next post).
Now: the sorts of questions that ignite the Battle of the Isms do look like perfectly good questions … for philosophers. But they are questions which get a lot of their bite, as I say, from worries about how maths hangs together with other things we tend to believe about the world and our knowledge of it. And the working mathematician is likely to think that, fine questions though they may be, s/he has quite enough nitty-gritty problems to think about within mathematics, thank you very much, and is far too busy to pause to worry about how what s/he’s up to relates to other areas of enquiry. So it’s division of labour time: let the philosophers get on with their own thing, building broad-brush ontological and epistemological stories about Life, the Universe, and Everything (including the place of maths); and let the mathematicians get on doing their more particular things. The philosophers had better know a smidgin about maths so their stories about how it fits into the Big Picture aren’t too unrealistic. But the mathematicians needn’t return the compliment, ’cos Big Picture stuff frankly isn’t their concern.
Right ….
Doesn’t that actually look a pretty sensible view, which would sustain the line that Imre and Thomas took (and indeed, between them, they made a few remarks suggesting this sort of picture)?
But still, for all that, I think we (qua mathematicians) should hesitate to be quite so quick to ignore the philosophers. For the simple truth is that philosophers in fact talk about much more than the Big Picture stuff. To be sure, the beginning undergraduate curriculum tends to concentrate in that region: e.g. for an excellent textbook see Stewart Shapiro’s very readable Thinking about Mathematics (OUP, 2000). But the philosophers also worry about questions like this: Have we any reason to suppose that the Continuum Hypothesis has a determinate truth-value? How do we decide on new axioms for set theory as we beef up ZFC trying to decide the likes of the Continuum Hypothesis? Anyway, what’s so great about ZFC as against other set theories (does it have a privileged motivation)? In what sense if any does set theory serve as a foundation for mathematics? Is there some sense in which topos theory, say, is a rival foundation? What kind of explanations/insights do very abstract theories like category theory give us? What makes for an explanatory proof in mathematics anyway? Is the phenomenon of mathematical depth just in the eye of the beholder, or is there something objective there? What are we to make of the reverse mathematics project (which shows that applicable mathematics can be founded in a very weak system of so-called predicative second-order arithmetic)? Must every genuine proof be formalisable (in the sort of way I talked about in the last post), and if so, using what grade of logical apparatus? Are there irreducibly diagrammatic proofs? …
I could go on. And on. But the point is already made. These questions, standing-back-a-bit and reflecting on our mathematical practice, can still reasonably enough be called philosophical questions (even if they don’t quite fit Sellars’s motto). They are more local than what I was calling the Big Picture questions — they don’t arise from looking over our shoulders and comparing mathematics with some other form of enquiry and wondering how they fit together, but rather the questions are internal to the mathematical enterprise. Yet certainly they are discussed by mathematically-minded people who call themselves philosophers as well as by philosophically-minded people who call themselves mathematicians (sometimes it is difficult to remember who is which, and some people call themselves both!). And the questions are surely worth some mathematicians thinking about some of the time. Which, thankfully, they do.
To be continued …
October 29, 2013
Does mathematics need a philosophy? — 1
At last week’s meeting of the Trinity Mathematical Society, Imre Leader and Thomas Forster gave introductory talks on “Does Mathematics need a Philosophy?” to a startlingly large audience, before a question-and-answer session. The topic is quite a big one, and the talks were very short. But here are a few after-thoughts (primarily for members of TMS, but others might be interested …).
(1) Imre did very briskly sketch a couple of recognizably philosophical views about mathematics, platonism and formalism. And he suggested that mathematicians tend to be platonist in their assumptions about what they are up to (in so far as they think they are exploring a determinate abstract mathematical universe, where there are objective truths to be discovered) but they turn formalist when writing up their proofs for public consumption. But I think that runs together formalism as an account of the nature of mathematics (“it’s all juggling with meaningless symbols, a game of seeing what symbol strings you can ‘deduce’ from other strings according to given rules”) with the project of formalization. Since I’ve more than once heard other mathematicians just make the same conflation, it’s worth pausing to pick it apart. (If some of the following sounds familiar, it is because I’m shamelessly plagiarizing my earlier self.)
To be sure, then, in presenting complex mathematical arguments, it helps to regiment our propositions into mathematical-English-plus-notation in ways which are expressly designed to be precise, free from obscurities, and where the logical structure of our claims is clear [think of the way we use the quantifier/variable notation -- as in  — to make the structure of statements of generality crystal clear]. Then we try to assemble our propositions into something approximating to a chain of formal deductions. Why? Because this enforces honesty: we have to keep a tally of the premisses we invoke, and of exactly what inferential moves we are using. And honesty is the best policy. Suppose we get from the given premisses to some target conclusion by inference steps each one of which is obviously valid (no suppressed premisses are smuggled in, and there are no suspect inferential moves). Then our honest toil then buys us the right to confidence that our premisses really do entail the desired conclusion. Hooray!
— to make the structure of statements of generality crystal clear]. Then we try to assemble our propositions into something approximating to a chain of formal deductions. Why? Because this enforces honesty: we have to keep a tally of the premisses we invoke, and of exactly what inferential moves we are using. And honesty is the best policy. Suppose we get from the given premisses to some target conclusion by inference steps each one of which is obviously valid (no suppressed premisses are smuggled in, and there are no suspect inferential moves). Then our honest toil then buys us the right to confidence that our premisses really do entail the desired conclusion. Hooray!
True, even the most tough-minded mathematics texts are written in an informal mix of ordinary language and mathematical symbolism. Proofs are very rarely spelt out in every formal detail, and so their presentation still falls short of the logicians’ ideal of full formalization. But we will hope that nothing stands in the way of our more informally presented mathematical proofs being sharpened up into fully formalized ones. Indeed, we might hope and pray that they could ideally be set out in a strictly regimented formal language of the kind that logicians describe (and which computer proofs implement), with absolutely every tiny inferential move made totally explicit, so that everything could be mechanically checked as being in accord with some overtly acknowledged rules of inference, with the proofs ultimately starting from our stated axioms.
True, the extra effort of laying out everything in complete detail will almost never be worth the cost in time and ink. In mathematical practice we use enough formalization to convince ourselves that our results don’t depend on illicit smuggled premisses or on dubious inference moves, and leave it at that — our motto is “sufficient unto the day is the rigour thereof”. Here are local heroes Whitehead and Russell making the point in Principia:
Most mathematical investigation is concerned not with the analysis of the complete process of reasoning, but with the presentation of such an abstract of the proof as is sufficient to convince a properly instructed mind.
(A properly instructed mind being, like them, a Trinity mathmo.)
Let’s all agree, then: formalization (at least up to a point) is a Good Thing, because a proof sufficiently close to the formalized ideal is just the thing you need in order to check that your bright ideas really do fly and then to convince the properly instructed minds of your readers. [Well, being a sort-of-philosophical remark, you'll be able to find some philosophers who seem to disagree, as is the way with that cantankerous bunch. But the dissenters are usually just making the point that producing formalizable proofs isn't the be-all and end-all of mathematics -- and we can happily agree with that. For a start, we often hanker after proofs that not only work but are in some way explanatory, whatever exactly that means.]
So Imre would have been dead right if he had said that mathematicians get to work (semi)-formalizing when they check and write up their proofs. But in fact, having described formalism as the game-with-meaningless-symbols idea, he said that mathematicians turn formalist in their proofs. Yet that’s a quite different claim.
Anyone who is tempted to run them together should take a moment to recall that one of the earliest clear advocates of the virtues of formalization was Frege, the original arch anti-formalist. But we don’t need to wheel out the historical heavy guns. The key point to make here is a very simple one. Writing things in a regimented, partially or completely symbolic, language (so that you can better check what follows from what) doesn’t mean that you’ve stopped expressing propositions and started manipulating meaningless symbols. Hand-crafted, purpose-designed languages are still languages. The move from ‘two numbers have the same same sum whichever way round you add them’ to e.g. ‘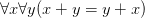 ’ changes the medium but not the message. And the fact that you can and should temporally ignore the meaning of non-logical predicates and functions while checking that a formally set-out proof obeys the logical rules [because the logical rules are formal!], doesn’t mean that non-logical predicates and functions don’t have a meaning!
’ changes the medium but not the message. And the fact that you can and should temporally ignore the meaning of non-logical predicates and functions while checking that a formally set-out proof obeys the logical rules [because the logical rules are formal!], doesn’t mean that non-logical predicates and functions don’t have a meaning!
In sum then, the fact that (on their best public behaviour) mathematicians take at least some steps towards making their proofs formally kosher doesn’t mean that they are being (even temporary) formalists.
Which is another Good Thing, because out-right naive formalism of the “it’s all meaningless symbols” variety is a pretty wildly implausible philosophy of mathematics. But that’s another story ….
To be continued
October 16, 2013
Stefan Collini writes again about the attack on universities
In the latest London Review of Books, Stefan Collini writes again from the heart and with critical incisiveness about the privatisation disasters befalling British universities. Here’s his peroration:
Future historians, pondering changes in British society from the 1980s onwards, will struggle to account for the following curious fact. Although British business enterprises have an extremely mixed record (frequently posting gigantic losses, mostly failing to match overseas competitors, scarcely benefiting the weaker groups in society), and although such arm’s length public institutions as museums and galleries, the BBC and the universities have by and large a very good record (universally acknowledged creativity, streets ahead of most of their international peers, positive forces for human development and social cohesion), nonetheless over the past three decades politicians have repeatedly attempted to force the second set of institutions to change so that they more closely resemble the first. Some of those historians may even wonder why at the time there was so little concerted protest at this deeply implausible programme. But they will at least record that, alongside its many other achievements, the coalition government took the decisive steps in helping to turn some first-rate universities into third-rate companies. If you still think the time for criticism is over, perhaps you’d better think again.
Read the article, weep, … and then if you are still in a UK academic job get a grip and do something!
Stefan Collini writes again on the attack on universities
In the latest London Review of Books, Stefan Collini writes again from the heart and with critical incisiveness about the disasters befalling British universities. Here’s his peroration:
Future historians, pondering changes in British society from the 1980s onwards, will struggle to account for the following curious fact. Although British business enterprises have an extremely mixed record (frequently posting gigantic losses, mostly failing to match overseas competitors, scarcely benefiting the weaker groups in society), and although such arm’s length public institutions as museums and galleries, the BBC and the universities have by and large a very good record (universally acknowledged creativity, streets ahead of most of their international peers, positive forces for human development and social cohesion), nonetheless over the past three decades politicians have repeatedly attempted to force the second set of institutions to change so that they more closely resemble the first. Some of those historians may even wonder why at the time there was so little concerted protest at this deeply implausible programme. But they will at least record that, alongside its many other achievements, the coalition government took the decisive steps in helping to turn some first-rate universities into third-rate companies. If you still think the time for criticism is over, perhaps you’d better think again.
October 7, 2013
Today wonderful reading: good fun!
If you follow @PeterSmith on Twitter — and why not? — these are apparently the delights that await you …
Logic and Schubert, eh? Can’t be bad.
Added: HT to Rowsety Moid for spotting the tagline I should have used to begin with!
Logic and Schubert
If you follow @PeterSmith — and why not? — these are apparently the delights that await you …
Logic and Schubert, eh? Can’t be bad.




