Peter Smith's Blog, page 106

Saffron Hall/Brodsky Quartet

We’ve just made our first visit to a concert at Saffron Hall, less than forty minutes from Cambridge. This is a multi-purpose hall newly built as part of Saffron Walden County High School and opened at the very end of last year. Once upon a long time ago, Mrs Logic Matters was at school there, and as we ordered interval drinks at the bar, she found herself standing again outside the head’s office, remembering being torn off a strip inside (mascara, too much; skirt, too short …).

But I digress. The Hall itself is large and the stage huge, as you can see, so the four music stands for the string quartet (and raised seat for the cellist)  looked very lost and lonely on the bare expanse. I worried that this space wasn’t going to work for such a small ensemble. Quite wrongly. The hall dimmed to leave the performers in a central pool of light. The acoustics were simply wonderful (apparently, there are state-of-the-art adjustable  acoustics). The sight lines were perfect. The general ambience was very engaging, with particularly friendly front-of-house volunteers.   There’s even a lot of parking. We were very impressed indeed with the Hall.

And the Brodskys? They began with Stravinsky’s short Three Pieces for String Quartet, new to me, and then gave a magical account of the fifth Shostakovich Quartet before the interval. Haunting and sensitively done. Bowled over. After the interval, however, the quartet played Death and the Maiden, and — by contrast — neither of us particularly warmed to their performance. (I had my doubts about the suitability of first violin’s playing style, and there wasn’t enough youthful fierceness either in the opening movement or the closing dance of death.) Still, the Shostakovich alone was more than worth the journey.

The main reason for posting this, however, is very warmly to encourage anyone within striking distance of Saffron Walden to check out the Hall’s programme of concerts over the next few months: Maria Joao Pires, The Sixteen, Ian Bostridge, Paul Lewis …  in a number of cases repeating a programme from the Wigmore Hall a few days before or after. A rather astonishing line up. The efforts of the new Director in her first season are more than worth supporting.

Quick book note: Pollard’s Mathematical Prelude to the Philosophy of Maths

“This book is based on two premises: one cannot understand philosophy of mathematics without understanding mathematics and one cannot understand mathematics without doing mathematics.” Thus the blurb of Stephen Pollard’s recent book A Mathematical Prelude to the Philosophy of Mathematics (Springer, 2014: xi + 202pp).

I certainly agree that if you want to study the philosophy of X, then it is pretty good idea to know something about X! And that applies in particular when X = mathematics. But in fact many serious philosophy departments do actually teach some relevant maths, in the guise of mathematical logic courses. Students can encounter core first-order logic up to a smidgin of model theory, variations/extensions such as intuitionistic logic and second-order logic, something about theories of arithmetic, theories of computable functions, and bit of set theory. True, these topics won’t necessarily be taught in the style of a hard-core maths course: the emphasis might be more on the Big Ideas and on conceptual foundations rather than on especially tricky problem-solving. But still, philosophy students who do tangle with the traditional menu of mathematical logic topics should acquire enough first-hand knowledge of enough serious mathematics for their philosophy of maths course to get some initial traction.

Of course, if elementary mathematical logic is all the maths you ever get to know, you’ll end up with a rather skewed view of the mathematical enterprise. But at least you’ve made a start. It is then a nice question what other maths it would be good for a budding philosopher of maths to acquire some small acquaintance with. Now, Pollard talks in his preface of the book’s “motley” character, which might suggest for a moment we are going to get an interestingly varied menu of topics, including some out of the usual run. But this isn’t really how things go. We in fact get three chapters on set theory, preceded by two chapters on arithmetic, and succeeded by another chapter on arithmetic and a chapter on intuitionistic logic. So in fact it is business pretty much as usual — mostly covering, though briefly, the sort of topics logicians typically cover for their philosophy students — albeit with some twists in the treatment of arithmetic which we’ll come to in a moment.

How then does this compare with other accounts of the familiar topics? Starting with the set theory chapters, Pollard fusses a lot at the outset, stressing that we shouldn’t be misled by unhappy metaphors of the “sets are like boxes” … variety, and recommending that we think of them as more like unordered list-types. And then he runs and runs with this idea, talking about “Zermelian lists” and more before reverting to standard set talk. But I didn’t find this particularly well done. And I frankly don’t think this, as an expository ploy, would be likely to work any better as an introduction to set theory than the standard approach of e.g. those wonderfully lucid entry-level books on set theory that I recommended in the TYL Guide.

The preceding chapter on first-order Peano Arithmetic is more conventional, but also rather compressed, and again there are significantly better options out there.

So that leaves three chapters to say just a little more about. The first chapter of the book is indeed unusual, for it starts by discussing Hilbert’s stroke arithmetic, so we get a discussion of tokens and types of tally marks, and then aims to develop primitive recursive arithmetic on this basis. The metaphysics of types here seems to get rather murky (types can be uninstantiated on p. 6, so they seem to be platonic universals at that point, but on p.7 it seems they are worldly enough for their existence to vary between worlds, so maybe not so platonic after all; and things aren’t really sorted out in Sec. 1.9 “Some Philosophy” ). Maybe we can work at extracting a clear position, but this is not what we want to be doing at this early point in what is supposed to be a maths book. Is this really the best way to introduce/motivate PRA? And indeed the ensuing development of PRA really could be clearer. So I’m not sure I’d want to recommend this chapter either.

But Pollard in his Preface does invite readers to pick and choose. And I so choose the last two chapters! The first of these takes us back to arithmetic after the excursus on set theory, but now to Frege Arithmetic. Students encountering the (neo)logicist programme in their philosophy of maths course could well find this presentation quite useful, as a companion piece to set alongside the Stanford Encyclopedia article. (I should note that, as in other chapters in the book, there are lots of comprehension-testing exercises as you go along, which some will find helpful.)

Then the final chapter goes off somewhat at a tangent, presenting a certain approach to intuitionist logic. This approach has its roots in the work of Gentzen, Prawitz, Dummett and Tennant, aiming to show that there is a particular naturalness to intuitionist logic if we think of the meaning of logical operators as given by their introduction rules, with elimination rules required to be harmonious (with this idea developed against the background of a certain way of thinking about negation and absurdity). But the particular version of the idea we get here is due to Jaroslav Peregrin, ‘What is the Logic of Inference?’ Studia Logica 88 (2008) 263-294. Pollard’s exposition is done with verve, and a student ought to find it both intriguing and illuminating. The best and most novel chapter in a rather patchy book, I think.

More logic, phil. maths, foundations blogs?

Brian Weatherson has an interesting new blogroll of “active philosophy blogs” with “substantive” content (where, sob, Logic Matters doesn’t get a mention — I must try harder, obviously, either to be more active or more philosophical). Inspired by that, I thought it was more than time to update the blogroll here. So alongside are now two short blogrolls to be going on with — scroll down the sidebar. One lists a few blogs with (occasional) logic/phil. maths/foundations of maths/or just maths content, the other links to a few other random favourites. (Hover your cursor over the blog title for a mini-description.)

The first list of logicky blogs is surprisingly short [Added: still short after an update, though I am being a bit selective]. Which probably simply reflects that I haven’t looked hard enough. So, folks, what am I missing? Any recommendations for (still active) blogs with good logic-related content??

Though actually, now I think about it, even Weatherson’s wide-ranging philosophy list is quite short, given the number of enthusiastic, energetic, philosophers out there. Perhaps the cool kids have moved on and blogs are no longer the done thing. A pity if so. They can be fun and illuminating for readers, and writers do get some ideas out there into the wider world (even a modest effort like Logic Matters counts its visitors per day in the many hundreds on the least generous of the stats counters).

[Added: with many thanks to @logicians on twitter, I've added a few more links, some I'd forgotten about, and one new to me.]

Quick book note: Stewart Shapiro’s Varieties of Logic

Stewart Shapiro’s very readable short book Varieties of Logic (OUP, 2014) exhibits the author’s characteristic virtues of great clarity and a lot of learning carried lightly. I found it, though, to be uncharacteristically disappointing.

Perhaps that’s because for me, in some key respects, he was preaching to the converted. For a start, I learnt long ago from Timothy Smiley that the notion of consequence  embraces a cluster of ideas. As Smiley puts it, the notion “comes with a history attached to it, and those who blithely appeal to an ‘intuitive’ or ‘pre-theoretic’ idea of consequence are likely to have got hold of just one strand in a string of diverse theories.” Debates, then, about which is the One True Notion of consequence are likely to be quite misplaced: for different purposes, in different contexts, we’ll want to emphasize and develop different strands, leading to different research programmes. As Shapiro puts it, the notion(s) of consequence can be sharpened in different ways — and taking that point seriously, he suggests, is already potentially enough to deflate some of the grand debates in the literature (e.g. about whether second-order logic is really logic).

And I’m still Quinean enough to find another of Shapiro’s themes congenial. Do we say, for example, that ‘or’ or ‘not’ mean the same for the intuitionist and the classical mathematician? Or is there a meaning-shift between the two? Shapiro argues that for certain purposes, in certain contexts, with certain interests in play, yes, we can say (if we like) that there is meaning shift; given other purposes/contexts/interests we won’t  say that. The notion of meaning is maybe too useful to do without in all kinds of situations; but it is also itself too shifting, too contextually pliable, to ground any grand debate here.

Put it this way, then. I’m pretty sympathetic with Shapiro’s claims that some large-scale grand debates are actually not very interesting because not well-posed. What that means, I take it, is that we’ll in fact find the interesting stuff going on a level or two down, below the topmost heights of cloudy generality, in areas where enough pre-processing has gone on to sharpen up ideas so that questions can be well-posed.

Here’s the sort of thing I mean. Take the very interesting debate between those like Prawitz, Dummett and Tennant who see a certain conception of inference and the logical enterprise as grounding only intuitionistic logic (leaving excluded middle as a non-logical extra, whose application to a domain is to be justified, if at all, on metaphysical grounds), and those like Smiley and Rumfitt who argue that that line of thought depends on failing to treat assertion and rejection on a par as we ought to do. This debate is prosecuted between parties who have agreed (at least for present purposes) on how to sharpen up certain ideas about logic, consequence, the role of connectives, etc.,  but still have an argument about how the research programme should proceed.

Shapiro doesn’t mention that particular debate. Absolutely fair enough (I just plucked out something that happens to interest me!). The complaint, though, is that he doesn’t supply us with much by way of other illustrations of investigations of varieties of logic at a level or two below the most arm-waving grand debates — i.e. at the levels where, by his own account, the real action must be taking place. Hence, I suppose, my general disappointment.

Shapiro does however mention a number of times one interesting example to provide grist to our mills, namely smooth infinitesimal analysis. This, if you don’t know it, is a deviant form of infinitesimal analysis — deviant, at any rate, from the mathematical mainstream. (If you look at Nader Vakil’s recent heavy volume Real Analysis Through Modern Infinitesimals  in the CUP series Encyclopedia of Mathematics and Its Applications, then you’ll find smooth analysis gets the most cursory of mentions in one footnote.) The key idea is that there are nil-potent infinitesimals — at a rough, motivational level, quantities so small their square is indeed zero, even though they are not assumed to be zero. More carefully, we have quantities 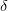such that  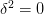and 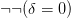, but — because the logic is intuitionistic — we can’t assert 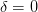. And then, the key assumption, it is required that for any function 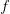, and number , there is a unique number 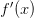such for any nil-potent 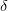, 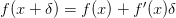. So looked at down at the infinitesimal level, 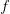is linear, and 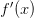gives its slope at — so is the derivative of 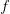. Now it turns out that, with enough assumptions in place, this theory allows us to define integration in a correspondingly natural way, and then we can readily prove the usual basic theorems of analysis.

Now that is indeed interesting. But — and here’s the rub — the internal intuitionistic logic is absolutely crucial. The usual complaint by the intuitionist is that adding the law of excluded middle unjustifiably collapses important distinctions (in particular the distinction between 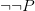and 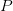).  But in the case of smooth analysis, add the law of excluded middle and the theory doesn’t just collapse (by making all the nil-potent infinitesimals identically zero) but becomes inconsistent. What are we to make of this? In particular, what can the defender of classical logic make of this?

I guess there is quite a lot to be said here. It is a nice question, for example, how much sense we can make of all this outside the topos-theoretic context where the Kock-Lawvere theory of smooth analysis had its original home. To be sure, as in John Bell’s A Primer of Infinitesimal Analysis, we can write down various axioms and principles and grind through deductions: but how much understanding ‘from the inside’ does that engender? Shapiro says just enough to pique a reader’s interest (for someone who hasn’t already come across smooth analysis), but not enough to leave them feeling they have much grip on what is going on, or to help out those who are already puzzling about the theory. And that’s a real disappointment.

Philosophers being offensive

If philosophers want to be really offensive, at least do it with style.

I’m reminded of a story about my favourite Cambridge philosopher, C.D. Broad. Not entirely a nice man.

A long time colleague of his at Trinity was the organic chemist Frederick Mann, whom Broad evidently thought an uncultured dullard. One evening at High Table, Broad finds himself unfortunately sitting opposite Mann. Broad beams cherubically. Pauses. And, to no-one in particular, sighs “Ah, where every prospect pleases …”.

The Very Short Teach Yourself Logic Guide

I seem to have gone full circle! The very first instalment of the TYL Study Guide was a short blogpost here. Then things grew. And grew. Until we get to the current 100 page PDF monster — and that’s only as short(!) as it is because some material has been exported to the Appendix and a supplementary webpage on Category Theory. Of course, the long version is full of good things, explains why the chosen texts are recommended, explains why others aren’t, suggests alternatives and supplementary reading, and more. But still, some might be interested in just getting the headline news.

So now, rather in the spirit of the original post, there’s an encouraging short and snappy page, The Very Short Teach Yourself Logic Guide, which just gives you the winners, the top recommendations for entry-level reading on the various areas of the core math. logic curriculum. (If you want to know why they are the winners, then you will have to look in the corresponding section of the full version of the Guide.)

Gillian Bennett: on doing the brave, decent and loving thing

If you happened not to see her final testimony and plea for the legalization of assisted suicide, then do read these very moving webpages left by Gillian Bennett (the wife for 57 years of that fine philosopher Jonathan Bennett) who faced with the ravages of dementia, ended her life last month.

One little “}”

No, you didn’t need new spectacles. One little “}” missing, and the last half of the lovingly crafted TYL version 12.0 was all in the smaller font intended for postscripts and asides. Pah! Sometimes is annoying. Just a tinsy bit.

OK, so here’s version 12.0a, which is at least easier on the eyes.

Teach Yourself Logic, version 12.0

In time for the new semester/new term/new academic year (depending on how things are chunked up in your neck of the woods), there’s a new version of the Teach Yourself Logic Study Guide and a supplementary page on Category Theory, both downloadable from the Guide’s usual page.

The Guide has been restructured into Parts in a different, more logical way, to make navigating though the 95 pages easier. There have been quite a few changes in the recommendations (e.g. on FOL and model theory). The final section on serious set theory has been restored and improved. There’s even now an index of authors’ names. What’s not to like?

The Guide seems to get used quite a lot (one previous version was downloaded almost three thousand times), which is why it seems well worth spending time on it occasionally. But I’m pretty happy with the current structure and content, so I hope that for a while the main Guide will only need minor tinkering to keep it in good shape (though there might be some more supplementary pages still to come).

As usual, please do let me know if you spot typos, or indeed if you have more substantive comments!

Model theory without tears?

Ah well, you win some and you lose some. I was writing for months about recursive ordinals and proof theory with a view to a short-ish book. And now, quite a way in, I realise that I have to go back to the drawing board, do a lot more thinking and reading if I am to have anything both interesting and true to say, and then (maybe) start over. Well, at least being retired I don’t have ‘research productivity’ (or whatever it is currently called) to worry about. Frustrating, though.

As a distraction, initially just with a view to updating one of the less convincing parts of the Teach Yourself Logic Guide in the next version, I’ve been looking again at some of the available treatments of elementary model theory. One immediate upshot is that there are now new pages on Jane Bridge’s Beginning Model Theory and (more substantially) on María Manzano’s Model Theory linked along with some other recent additions at the Book Notes page.

Now, the books by Bridge and Manzano have their virtues, of course, as do some other accounts at the same kind of level, But still, the more I read, the more tempted I am to put my hand to trying to write my own Beginning Model Theory (or maybe that should be Model Theory Without Tears alongside Gödel Without Tears). The exegetical space between a basic treatment of first-order logic and the rather sophisticated delights of (say) Wilfrid Hodges’s Shorter Model Theory and David Marker’s Model Theory isn’t exactly crowded with good texts, and it would be fun to have a crack at. And unlike the recursive ordinals project, at least I think I understand what needs to be said! Which is a good start …