Peter Smith's Blog, page 103

Blue Monica

Monica Vitti — for those who still end up at Logic Matters because of that little flurry of pictures of that icon of the Italian films of my youth which I posted a few years ago.

A little problem in high school geometry

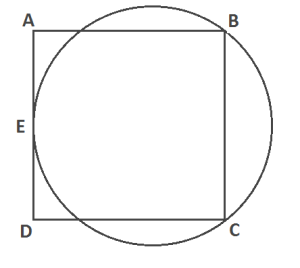Let E be the midpoint of the side AD of a square ABCD.

Problem: Determine which has the greater perimeter, the square ABCD or the circle through E, B, C?  (You can assume you know the value of π. Otherwise try to use elementary methods.)

The neat solution is, I think,  rather satisfying, even though it doesn’t require any special ingenuity to find it. Metaproblem: Why is this solution aesthetically pleasing?

The answer — to the problem, if not the metaproblem —  is below the fold: but try blowing the dust of your school geometry before looking at the cheat sheet!

OK: obviously we need to compare the diameter of the circle with the side of the square. But we haven’t yet got a diameter drawn — so put in the obvious one, through E to the opposite side of the circle at F, with EF intersecting BC at G.

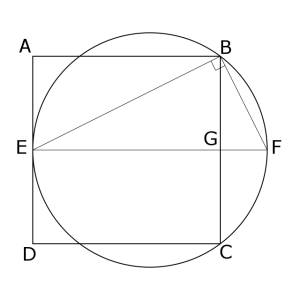The hint was “use elementary methods”, which in the first year of geometry typically means drawing some triangles, and using basic facts about similar triangles, angles of triangles inscribed in circles, etc. So the absolutely obvious next thing to do is to draw a triangle to get the augmented diagram.

Now we know that |BG| = |AE| = |EG|/2. And it is entirely elementary that EGB and BGF are similar. So |FG|/|BG| = |BG|/|EG|. From these two facts we immediately have |FG| = |EG|/4.

Set |EG| to be one unit. Then the perimeter of the square is 4, and the perimeter of the circle is π5/4

That is — you would have thought — entirely straightforward. But the proof is also rather satisfying, possibly easier than you were expecting, as it uses minimal input. You don’t need to know about Cartesian coordinates or anything like that.

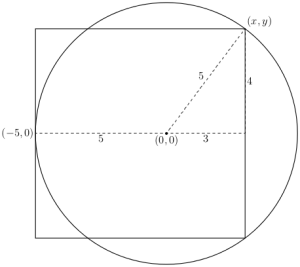It was therefore interesting (and to an extent puzzling) to see that when this question was posed on math.stackexchange and taken up on reddit answers were all over the place. And the most upvoted answer was initially one that depended on it just dawning on you (from your familiarity with Pythagorean triangles) that the situation must be as diagrammed on the left. So the perimeter of the square is (in those units) 32, and of the circle is 2π.5. But such guesswork doesn’t make for an elegant proof, even if in this case your very first guess might deliver the goods. We can remove the guesswork by applying brute force and the Pythagorean theorem to the diagram on the right. 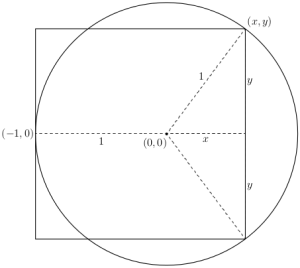And now we just use the facts that 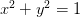and 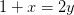and do the algebra. But that is still, surely, not at all such a neat proof as our original one.

What this illustrates, anyway, is perhaps that satisfying proofs don’t have to be ingenious or depend on unexpected tricks. Sometimes, the aesthetic pleasure comes from slightly surprising simplicity and economy of means.

[Diagrams snaffled from math.stackexchange!]

 

A nice problem in high school geometry

Let E be the midpoint of the side AD of a square ABCD.

Problem: Determine which has the greater perimeter, the square ABCD or the circle through E, B, C?  (You can assume you know the value of π. Otherwise try to use elementary methods.)

The neat solution is obvious when you spot it, and I find rather satisfying. Metaproblem: Why is this solution aesthetically pleasing?

I’ll post the answer — to the problem, if not the metaproblem —  tomorrow!

Category theory: status report

It is an irksome habit, and I wish I could break it and plough on regardless. But I always find when writing anything lengthy that there comes a point by which I’ve accumulated enough little niggling worries about things I’ve already said that I just have to go back to page one and work through again from the beginning, ironing things out. So that’s what I’m doing at the moment with my category theory notes. The exercise is — surprise, surprise! — taking longer than expected, but I hope has made for some interesting expository changes, about which more in due course, when the revised/expanded notes are ready for prime time.

Meanwhile, here’s an update/expansion of the page on Category Theory giving links to (broadly speaking) student-orientated materials available online.

893 posts later …

The Logic Matters blog started, back in the olden days, on March 9, 2006. It’s our ninth birthday. Will there be cake?

So here we are, at post number 894. The two stats packages which monitor Logic Matters give very disparate results, but a thousand or two people come to the site each day, and if there is a mention on reddit, for example, that number can jump well into the tens of thousands. And the stats agree that in the last five years, visits to the site in general and the blog in particular have gone up four-fold. So I seem to get to corrupt the minds of the youth spread the logical word to many more here than I ever did in my teaching career. Which makes it fun and all worth the effort.

Onwards!

David Fray plays Schubert: Fantaisie

I buy far too many CDs and go to a fair number of concerts, and so I usually blog only about some of the ‘five star’ discs or concerts which bowl me over. Which does mean that when I do write, my reviews (such as they are) tend to be consistently full of superlatives. It is certainly not that I’m an uncritical listener: very far from it. Still, I don’t want to be carping, or to be tediously negative here. I prefer to write from heartfelt enthusiasm. And this time, it is for David Fray’s latest CD.

One of the very finest Schubert recordings of the last ten years is Fray’s CD of the Op 92 Impromptus and the Moments Musicaux. He plays those pieces with luminous artistry and acute sensitivity — taking some notably slow tempi yet never seeming mannered or other than fully immersed in the complexities and ambiguities of Schubert’s music. There is, I have remarked elsewhere, something Richter-like in Fray’s intensity, and in his wonderful ability to impose his vision of the music.

Fray has now returned to Schubert, and indeed firstly to a piece indelibly associated with a quite extraordinary recording by Richter — the G major sonata D894. And the comparison in some ways is still very apt. For like Richter, Fray plays the first movement with great expansiveness. Where, for example,  Brendel in his later digital recording takes 17′.16″ and Paul Lewis 17′.28″ — both very fine performances — Fray takes 19′.06″. This still falls far short of Richter’s astonishing, bordering-on-the-perverse, 26′.51″ in the (in)famous 1979 recording. Yet here is the magical thing: from Fray’s way with his very slight holdings-back, the slightest hesitations, to his control of the architecture of the movement, everything gives his performance a seeming scale closer to Richter’s. (He takes little more than half a minute more than Mitsuko Uchida’s 18′.29″ and yet Fray’s first movement  at crucial moments seems markedly more spacious.)

Another magical thing: the wonderfully nuanced clarity of Fray’s playing here —  effortlessly cantabile passage work, forte passages which never become brashly declamatory, unending attention to detail with nothing exaggerated or out of place.

Now, there can be a problem — can’t there? — with performances of some of Schubert’s major works: how to make a satisfying whole of a piece that starts with one or two immense movements — immense both in scale and emotional weight. (One of the many things that I particularly admire about the Pavel Haas Quartet’s Schubert CD which I reviewed here is the extraordinarily balance they achieve across the four movements of Death and the Maiden and again of the String Quintet.) How does the rest of David Fray’s performance of the ‘Fantasie’ sonata hold up against this test?

Extraordinarily well, I would say. I was rather surprised, when I checked, that Fray’s timings in the remaining three movements are rather quicker than Brendel, Lewis and Uchida. Yet he plays with such grace and attention to texture and detail that Schubert’s music is given all the space it needs, and there are again quite magical touches. The Trio in the third movement catches with your breath. The final Allegretto dances through its episodes with an exquisite lightness of touch in building to its conclusion.

In short, I would say that of the dozen or more great performances of the G major sonata that I have on disc, this is at least as fine as any: it is worth getting Fray’s new CD for this alone.

But there is more. Fray follows with a lovely performance of the Hungarian Melody D817. And then for the last two major pieces on the CD he is joined by his one-time teacher Jacques Rouvier. First, they play the Fantasia in F minor D940. This, the incurable romantics among us will remember, was dedicated by Schubert to his young pupil the Countess Karoline Esterházy, often thought to have been the object of his hopeless love: and the piece certainly calls for yearning and passion. I have long loved the old recording from 1978 by Imogen Cooper and Anne Queffélec. But Fray and Rouvier are perhaps even better. Certainly, the yearning in the first dotted theme (with its Hungarian echoes) is as heartfelt; the passion as the music then goes through its evolving moods — stormy, a burst of sunshine, clouds regathering interspersed with more moments of fleeting happiness — is as intense; the moment when the first yearning theme returns is as affecting; the build-up through the fugato passage to the very final appearance of the initial theme as the music comes to its abrupt recognition that the yearning is indeed hopeless, all this is wonderfully well done.

The CD concludes with the ‘Lebensstürme’ Allegro D947. Not, for whatever reason, my favourite Schubert piano music: but again this surely it could not be played better than it is here.

A wonderful disc then, most warmly recommended.  (And there is, by the way, a video about this CD on David Fray’s website.)

Category theory again

The category theory page here has been much expanded with links to (i) some online lecture notes, and (ii) some books which are freely (and legitimately!) available online in one form or another.

I am not at all aiming to include everything that is available out there: but on the other hand, if I have missed something good, do please let me know!

The Pavel Haas Quartet at the Wigmore Hall

To the Wigmore Hall again last week to see hear the Pavel Haas Quartet playing Czech music old and new. The most engaging concert, we agreed, that we’d been to for months.

To begin, Dvorak’s four Miniatures Op. 75a for two violins and viola (not so much a trio as pieces for violin accompanied by the other two strings). These were played just perfectly by Veronika Jaruskova with quite extraordinary lyrical beauty in the final movement, making something really rather special out of these charming miniatures. Then into the first Janacek String Quartet, ‘Kreutzer Sonata’, with this often jaggedly urgent and restless music played with the PHQ’s characteristic controlled passion and commitment. The quartet’s ensemble, their unity in tone, is quite extraordinary.

The PHQ were then joined by Colin Currie for the UK première of a piece commissioned for them, Jiri Gemrot’s Quintet for two violins, viola, cello and marimba. The sound world of the marimba sometimes interweaving with the strings, sometimes set against strong chordal writing for the quartet, was captivating and often very exciting. The atomspheric slow movement in particular produced quite some magical sounds: “the first violin sings with an eerie, disembodied voice to a hypnotic accompaniment from the marimba”, as the FT reviewer puts it. We perhaps weren’t always convinced by the piece, although it somehow sounded so very Czech — occasionally the writing for the strings seemed too blocky, when more imaginative textures could have been developed. But the playing was just superb, and we’d most certainly go to hear the Quintet performed again.

After the interval, the Pavel Haas played Pavel Haas, the second quartet ‘From the Monkey Mountains’, the one which features percussion in the last movement. This was, as we would hope and expect, a quite peerless performance of a very piece (a few years ago we could have said ‘neglected masterpiece’, so we owe PHQ much for championing Pavel Haas’s quartets).

A five star concert, then. And the audience rightly gave the PHQ the warmest, cheering, applause at the end. I hope they felt properly appreciated. For we only half filled the Hall, albeit in the middle of the week on a chill night. Which is a bit depressing when it is one of the world’s very greatest quartets, surely getting to the height of their considerable powers, and offering a programme which was engaging rather than challenging.

I just regret that we couldn’t go back to hear them again in another Bohemian programme on Saturday (though we’ve already pencilled in their next two concerts at the Wigmore): for the moment, we’ll just have to look forward to the PHQ’s Smetena CD which is due out a little later this year.

Notes on Category Theory v.4

I wasn’t able to do much work in January for family reasons, but levels of concentration and energy are returning. So, much later than I’d hoped, here at last is an updated version of the Notes on Category Theory (still very partial though now 109 pp.). There are three newly added chapters, and some minor tinkering earlier. We now cover:

Categories defined
Duality, kinds of arrows (epics, monics, isomorphisms …)
Functors
More about functors and categories (and the category of categories!)
Natural transformations (with rather more than usual on the motivation)
Equivalence of categories (again with a section on motivation, why we want ‘equivalence’ rather than full isomorphism)
The Yoneda embedding (shown to indeed be an embedding by using an easy restricted version of the Yoneda Lemma)
An aside on Cayley’s Theorem
The Yoneda Lemma (how to get to the full-dress version by two conceptually easy steps from the restricted version).
Representables (definitions, examples, universal elements, the category of elements).
First examples of limits (terminal objects, products, equalizers and their duals)
Limits and colimits defined (cones, limit cones: pullbacks and upshots)
The existence of limits (in particular, having finite products and equalizers implies having all finite limits).

Coming soon: a further chapter on limits (on functors and the preservation of limits) and then a chapter on Galois connections as a nice gentle lead-in to the chapters on adjoints.

What is the category Set?

We all know that we quickly encounter issues of size when we start category theory. Categories, we are told, are collections of objects and morphisms satisfying certain axioms. But we very soon meet, among our very first examples of categories, categories like Set whose objects are too many for the collection of them to itself be a set. So what kind of ‘collection’ do we have here?

But here’s another issue about that initial example of the category Set which is ignored by many writers of introductory texts.

The issue can be posed, bluntly, like this: when the category Set is mentioned early on in an introductory text what category is that?

Typically no explanation is given at this stage. But of course which category we are dealing with depends on our set theory. For an NF-iste, the category of NFsets has very different properties from what is intended (for a start NFsets is not cartesian closed and later we learn that  Set is). But fair enough, in an intro book you aren’t going to mention that in the opening pages! Rather the authors are, surely, intending to point to stuff that their beginning readers can be assumed to know about, and are saying, “Hey you in fact already know about some categories, for example …” The charitable reading, then, is that authors are relying on their readers to think of  Set as comprising the sets they already know and love.

But what sets are those?

Well, for many readers (if they have done any more than had a bit of set-notation waved at them) the sets they know and love are the  pure sets of the cumulative hierarchy — pure in that there are no urlements, no memberless entities in the universe of sets other than the empty sets. If set theories with urelements are mentioned in passing in an intro set-theory course, it is usually only to be dismissed and forgotten about. So: in the absence of special explicit signals to the contrary, it seems (doesn’t it?) that we might reasonably take the category Set mentioned in the very early pages to be a category of pure sets of the usual hierarchy (or at least the hierarchy up to some inaccessible, or whatever). Just sometimes this is made explicit. Thus, Horst Schubert in his terse but very good and clear Categories (§3.1) writes “One has to be aware that the set theory used here has no “primitive (ur-) elements”; elements of sets, or classes …, are always themselves sets.”

But then what are we to make, a bit later in our introductory books, of e.g. the usual presentation of the Yoneda embedding as . Putting it this way, if you look at the details, assumes that hom-collections 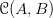for 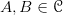actually live in . And since such a hom-collection is a set of -morphisms, that assumes that the 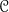-morphisms must live in the world of pure sets too. [Sure, we may want the relevant hom-collections to be set-sized in the Yoneda embedding case — but being no bigger than set-sized is one thing, living in the universe of pure sets is something else!]

But do we really want to assume that morphisms are always pure sets?

Might we not be looking to category theory for a story about how different bits of the mathematical universe hang together which need not presuppose some over-arching, all-in, set-theoretic reductionism, and so in particular doesn’t presuppose from day one that all morphisms are pure sets?

Now, as I noted, the foundational sections you often meet early in category theory books worry away about questions of size (sets vs classes etc.). But the present worry is orthogonal to all that, and is in a way more basic. If we want to make no assumption that the denizens of different bits of the mathematical universe are all cut from the same cloth, we won’t want to slip into assuming that sets of these denizens are all pure sets. So in particular, do we really want to assume that a collection of morphisms (hom-set) must actually live in Set, if that’s the category mentioned back almost on p.1 of the book which is naturally read (and sometimes explicitly said to be) a category of pure sets? It may be that Set eventually gets to play a special role in the mathematical universe, with other most other categories being representable inside it: but surely this should be something to be shown later, not an assumption to be built in from the start.

In Chapter 3 of his fine Basic Category Theory, Tom Leinster makes the right moves here. Back track. What are the sets that, before we start into category theory, we know and love and which are pointed to as constituting an exemplar of a category? Not the sets of pure ZFC (which mathematicians other than set theorists could even spell out the axioms which are supposed to tell you what these are?) but rather what we might call the sets of the working mathematician — sets of naturals, perhaps, or sets of reals, or sets of points in a space, or a set of continuous functions, or … And these are sets with ur-elements, elements that are not themselves presumed to be sets. (Or if we ascend to talk of sets of sets of naturals, for example, it remains the case that when we descend again through members of members … everything typically bottoms out with primitive non-sets.)

We assume various operations are permissible on these sets, and we can codify the permissible operations (for the purposes of the non-set-theorist, falling short of ZFC). Now Leinster associates this with Lawvere’s codification of the Elementary Theory of the Category of Sets (ETCS). But of course, Zermelo was in the same game, aiming to codify the principles of set-building that the working mathematician actually needs, aiming to provide enough to do the usual constructions but not enough to threaten paradox, and Zermelo’s original set theory too allowed for ur-elements. But then, if Set is to be a category of sets-with-urelements, built up using the principles working mathematicians actually need (whatever they are) — which indeed makes some of appeals to Set in category theory much more natural — then this really needs to be said (as Leinster does, and others don’t, and some actually deny).

Of course, we could go Schubert’s way and take hom-sets to be pure sets, so that morphisms and the other apparatus of category theory are all pure sets. But seeing category theory in this way as simply in the service of an across-the-board set-theoretic reductionism would surely be an unhappy way of looking at things: category theory seemed to promise more than that!