Metin Bektas's Blog: Metin's Media and Math - Posts Tagged "physics"
Intensity (or: How Much Power Will Burst Your Eardrums?)
Under ideal circumstances, sound or light waves emitted from a point source propagate in a spherical fashion from the source. As the distance to the source grows, the energy of the waves is spread over a larger area and thus the perceived intensity decreases. We'll take a look at the formula that allows us to compute the intensity at any distance from a source.
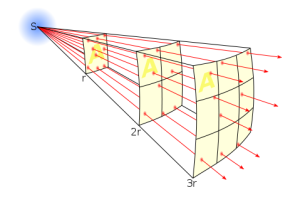
First of all, what do we mean by intensity? The intensity I tells us how much energy we receive from the source per second and per square meter. Accordingly, it is measured in the unit J per s and m² or simply W/m². To calculate it properly we need the power of the source P (in W) and the distance r (in m) to it.
I = P / (4 · π · r²)
This is one of these formulas that can quickly get you hooked on physics. It's simple and extremely useful. In a later section you will meet the denominator again. It is the expression for the surface area of a sphere with radius r.
Before we go to the examples, let's take a look at a special intensity scale that is often used in acoustics. Instead of expressing the sound intensity in the common physical unit W/m², we convert it to its decibel value dB using this formula:
dB ≈ 120 + 4.34 · ln(I)
with ln being the natural logarithm. For example, a sound intensity of I = 0.00001 W/m² (busy traffic) translates into 70 dB. This conversion is done to avoid dealing with very small or large numbers. Here are some typical values to keep in mind:
0 dB → Threshold of Hearing
20 dB → Whispering
60 dB → Normal Conversation
80 dB → Vacuum Cleaner
110 dB → Front Row at Rock Concert
130 dB → Threshold of Pain
160 dB → Bursting Eardrums
No onto the examples.
----------------------
We just bought a P = 300 W speaker and want to try it out at maximal power. To get the full dose, we sit at a distance of only r = 1 m. Is that a bad idea? To find out, let's calculate the intensity at this distance and the matching decibel value.
I = 300 W / (4 · π · (1 m)²) ≈ 23.9 W/m²
dB ≈ 120 + 4.34 · ln(23.9) ≈ 134 dB
This is already past the threshold of pain, so yes, it is a bad idea. But on the bright side, there's no danger of the eardrums bursting. So it shouldn't be dangerous to your health as long as you're not exposed to this intensity for a longer period of time.
As a side note: the speaker is of course no point source, so all these values are just estimates founded on the idea that as long as you're not too close to a source, it can be regarded as a point source in good approximation. The more the source resembles a point source and the farther you're from it, the better the estimates computed using the formula will be.
----------------------
Let's reverse the situation from the previous example. Again we assume a distance of r = 1 m from the speaker. At what power P would our eardrums burst? Have a guess before reading on.
As we can see from the table, this happens at 160 dB. To be able to use the intensity formula, we need to know the corresponding intensity in the common physical quantity W/m². We can find that out using this equation:
160 ≈ 120 + 4.34 · ln(I)
We'll subtract 120 from both sides and divide by 4.34:
40 ≈ 4.34 · ln(I)
9.22 ≈ ln(I)
The inverse of the natural logarithm ln is Euler's number e. In other words: e to the power of ln(I) is just I. So in order to get rid of the natural logarithm in this equation, we'll just use Euler's number as the basis on both sides:
e^9.22 ≈ e^ln(I)
10,100 ≈ I
Thus, 160 dB correspond to I = 10,100 W/m². At this intensity eardrums will burst. Now we can answer the question of which amount of power P will do that, given that we are only r = 1 m from the sound source. We insert the values into the intensity formula and solve for P:
10,100 = P / (4 · π · 1²)
10,100 = 0.08 · P
P ≈ 126,000 W
So don't worry about ever bursting your eardrums with a speaker or a set of speakers. Not even the powerful sound systems at rock concerts could accomplish this.
----------------------
This was an excerpt from the ebook "Great Formulas Explained - Physics, Mathematics, Economics", released yesterday and available here: http://www.amazon.com/dp/B00G807Y00.

First of all, what do we mean by intensity? The intensity I tells us how much energy we receive from the source per second and per square meter. Accordingly, it is measured in the unit J per s and m² or simply W/m². To calculate it properly we need the power of the source P (in W) and the distance r (in m) to it.
I = P / (4 · π · r²)
This is one of these formulas that can quickly get you hooked on physics. It's simple and extremely useful. In a later section you will meet the denominator again. It is the expression for the surface area of a sphere with radius r.
Before we go to the examples, let's take a look at a special intensity scale that is often used in acoustics. Instead of expressing the sound intensity in the common physical unit W/m², we convert it to its decibel value dB using this formula:
dB ≈ 120 + 4.34 · ln(I)
with ln being the natural logarithm. For example, a sound intensity of I = 0.00001 W/m² (busy traffic) translates into 70 dB. This conversion is done to avoid dealing with very small or large numbers. Here are some typical values to keep in mind:
0 dB → Threshold of Hearing
20 dB → Whispering
60 dB → Normal Conversation
80 dB → Vacuum Cleaner
110 dB → Front Row at Rock Concert
130 dB → Threshold of Pain
160 dB → Bursting Eardrums
No onto the examples.
----------------------
We just bought a P = 300 W speaker and want to try it out at maximal power. To get the full dose, we sit at a distance of only r = 1 m. Is that a bad idea? To find out, let's calculate the intensity at this distance and the matching decibel value.
I = 300 W / (4 · π · (1 m)²) ≈ 23.9 W/m²
dB ≈ 120 + 4.34 · ln(23.9) ≈ 134 dB
This is already past the threshold of pain, so yes, it is a bad idea. But on the bright side, there's no danger of the eardrums bursting. So it shouldn't be dangerous to your health as long as you're not exposed to this intensity for a longer period of time.
As a side note: the speaker is of course no point source, so all these values are just estimates founded on the idea that as long as you're not too close to a source, it can be regarded as a point source in good approximation. The more the source resembles a point source and the farther you're from it, the better the estimates computed using the formula will be.
----------------------
Let's reverse the situation from the previous example. Again we assume a distance of r = 1 m from the speaker. At what power P would our eardrums burst? Have a guess before reading on.
As we can see from the table, this happens at 160 dB. To be able to use the intensity formula, we need to know the corresponding intensity in the common physical quantity W/m². We can find that out using this equation:
160 ≈ 120 + 4.34 · ln(I)
We'll subtract 120 from both sides and divide by 4.34:
40 ≈ 4.34 · ln(I)
9.22 ≈ ln(I)
The inverse of the natural logarithm ln is Euler's number e. In other words: e to the power of ln(I) is just I. So in order to get rid of the natural logarithm in this equation, we'll just use Euler's number as the basis on both sides:
e^9.22 ≈ e^ln(I)
10,100 ≈ I
Thus, 160 dB correspond to I = 10,100 W/m². At this intensity eardrums will burst. Now we can answer the question of which amount of power P will do that, given that we are only r = 1 m from the sound source. We insert the values into the intensity formula and solve for P:
10,100 = P / (4 · π · 1²)
10,100 = 0.08 · P
P ≈ 126,000 W
So don't worry about ever bursting your eardrums with a speaker or a set of speakers. Not even the powerful sound systems at rock concerts could accomplish this.
----------------------
This was an excerpt from the ebook "Great Formulas Explained - Physics, Mathematics, Economics", released yesterday and available here: http://www.amazon.com/dp/B00G807Y00.
Hollywood and Physics
We've all seen these kinds of movies. After a fast and dramatic chase, the bad guy jumps out of the car, determined to end the good guy once and for all. His evil plans have been thwarted for the last time! In self-defense, the good guy is forced to take a shot and when the bullet hits, the evildoer is thrown violently backwards as a result of the impact and through the nearest shop window. Once the hero is reunited with the love of his life, the credits roll and we are left to wonder if that's really how physics work.
In a previous example we calculated the momentum of a common 9 mm bullet (p = 5.4 kg m/s). Suppose the m = 75 kg evildoer gets hit by just this bullet. Since the bullet practically comes to a halt on impact, this momentum has to be transferred to the unlucky antihero for the conservation of momentum to hold true. Accordingly, this is the speed at which the bad guy is thrown back:
5.4 kg m/s = 75 kg · v'
v' ≈ 0.07 m/s ≈ 0.26 km/h ≈ 0.16 mph
This is not even enough to topple a person, let alone make him fly dramatically through the air. From a kinematic point of view, the impact is not noticeable. The same is true for more massive and faster bullets as well as for a series of impacts. The only thing that can make a person fall instantly after getting shot is a sudden drop in blood pressure and the resulting loss of consciousness. But in this case, the evildoer would simply drop where he stands instead of being thrown backwards.
This is not the only example of Hollywood bending the laws of physics. You've probably heard the weak "fut" sound a Hollywood gun makes when equipped with a silencer. This way the hero can take out an entire army of bad guys without anyone noticing. But that's not how pistol silencers work. At best, they can reduce the the sound level to about 120 dB, which is equivalent to what you hear standing near a pneumatic hammer or right in front of the speakers at a rock concert. So unless the hero is up against an army of hearing impaired seniors (which wouldn't make him that much of a hero), his coming will be noticed.
(This was an excerpt from Physics! In Quantities an Examples)
In a previous example we calculated the momentum of a common 9 mm bullet (p = 5.4 kg m/s). Suppose the m = 75 kg evildoer gets hit by just this bullet. Since the bullet practically comes to a halt on impact, this momentum has to be transferred to the unlucky antihero for the conservation of momentum to hold true. Accordingly, this is the speed at which the bad guy is thrown back:
5.4 kg m/s = 75 kg · v'
v' ≈ 0.07 m/s ≈ 0.26 km/h ≈ 0.16 mph
This is not even enough to topple a person, let alone make him fly dramatically through the air. From a kinematic point of view, the impact is not noticeable. The same is true for more massive and faster bullets as well as for a series of impacts. The only thing that can make a person fall instantly after getting shot is a sudden drop in blood pressure and the resulting loss of consciousness. But in this case, the evildoer would simply drop where he stands instead of being thrown backwards.
This is not the only example of Hollywood bending the laws of physics. You've probably heard the weak "fut" sound a Hollywood gun makes when equipped with a silencer. This way the hero can take out an entire army of bad guys without anyone noticing. But that's not how pistol silencers work. At best, they can reduce the the sound level to about 120 dB, which is equivalent to what you hear standing near a pneumatic hammer or right in front of the speakers at a rock concert. So unless the hero is up against an army of hearing impaired seniors (which wouldn't make him that much of a hero), his coming will be noticed.
(This was an excerpt from Physics! In Quantities an Examples)
Einstein’s Special Relativity – The Core Idea
It might surprise you that a huge part of Einstein’s Special Theory of Relativity can be summed up in just one simple sentence. Here it is:
“The speed of light is the same in all frames of references”
In other words: no matter what your location or speed is, you will always measure the speed of light to be c = 300,000,000 m/s (approximate value). Not really that fascinating you say? Think of the implications. This sentence not only includes the doom of classical physics, it also forces us to give up our notions of time. How so?
Suppose you watch a train driving off into the distance with v = 30 m/s relative to you. Now someone on the train throws a tennis ball forward with u = 10 m/s relative to the train. How fast do you perceive the ball to be? Intuitively, we simply add the velocities. If the train drives off with 30 m/s and the ball adds another 10 m/s to that, it should have the speed w = 40 m/s relative to you. Any measurement would confirm this and all is well.
Now imagine (and I mean really imagine) said train is driving off into the distance with half the light speed, or v = 0.5 * c. Someone on the train shines a flashlight forwards. Obviously, this light is going at light speed relative to the train, or u = c. How fast do you perceive the light to be? We have the train at 0.5 * c and the light photons at the speed c on top of that, so according to our intuition we should measure the light at a velocity of v = 1.5 * c. But now think back to the above sentence:
“The speed of light is the same in all frames of references”
No matter how fast the train goes, we will always measure light coming from it at the same speed, period. Here, our intiution differs from physical reality. This becomes even clearer when we take it a step further. Let’s have the train drive off with almost light speed and have someone on the train shine a flashlight forwards. We know the light photons to go at light speed, so from our perspective the train is almost able to keep up with the light. An observer on the train would strongly disagree. For him the light beam is moving away as it always does and the train is not keeping up with the light in any way.
How is this possible? Both you and the observer on the train describe the same physical reality, but the perception of it is fundamentally different. There is only one way to make the disagreement go away and that is by giving up the idea that one second for you is the same as one second on the train. If you make the intervals of time dependent on speed in just the right fashion, all is well.
Suppose that one second for you is only one microsecond on the train. In your one second the distance between the train and the light beam grows by 300 meter. So you say: the light is going 300 m / 1 s = 300 m/s faster than the train.
However, for the people in the train, this same 300 meter distance arises in just one microsecond, so they say: the light is going 300 m / 1 µs = 300 m / 0.000,001 s = 300,000,000 m/s faster than the train – as fast as it always does.
Note that this is a case of either / or. If the speed of light is the same in all frames of references, then we must give up our notions of time. If the light speed depends on your location and speed, then we get to keep our intiutive image of time. So what do the experiments say? All experiments regarding this agree that the speed of light is indeed the same in all frames of references and thus our everyday perception of time is just a first approximation to reality.
“The speed of light is the same in all frames of references”
In other words: no matter what your location or speed is, you will always measure the speed of light to be c = 300,000,000 m/s (approximate value). Not really that fascinating you say? Think of the implications. This sentence not only includes the doom of classical physics, it also forces us to give up our notions of time. How so?
Suppose you watch a train driving off into the distance with v = 30 m/s relative to you. Now someone on the train throws a tennis ball forward with u = 10 m/s relative to the train. How fast do you perceive the ball to be? Intuitively, we simply add the velocities. If the train drives off with 30 m/s and the ball adds another 10 m/s to that, it should have the speed w = 40 m/s relative to you. Any measurement would confirm this and all is well.
Now imagine (and I mean really imagine) said train is driving off into the distance with half the light speed, or v = 0.5 * c. Someone on the train shines a flashlight forwards. Obviously, this light is going at light speed relative to the train, or u = c. How fast do you perceive the light to be? We have the train at 0.5 * c and the light photons at the speed c on top of that, so according to our intuition we should measure the light at a velocity of v = 1.5 * c. But now think back to the above sentence:
“The speed of light is the same in all frames of references”
No matter how fast the train goes, we will always measure light coming from it at the same speed, period. Here, our intiution differs from physical reality. This becomes even clearer when we take it a step further. Let’s have the train drive off with almost light speed and have someone on the train shine a flashlight forwards. We know the light photons to go at light speed, so from our perspective the train is almost able to keep up with the light. An observer on the train would strongly disagree. For him the light beam is moving away as it always does and the train is not keeping up with the light in any way.
How is this possible? Both you and the observer on the train describe the same physical reality, but the perception of it is fundamentally different. There is only one way to make the disagreement go away and that is by giving up the idea that one second for you is the same as one second on the train. If you make the intervals of time dependent on speed in just the right fashion, all is well.
Suppose that one second for you is only one microsecond on the train. In your one second the distance between the train and the light beam grows by 300 meter. So you say: the light is going 300 m / 1 s = 300 m/s faster than the train.
However, for the people in the train, this same 300 meter distance arises in just one microsecond, so they say: the light is going 300 m / 1 µs = 300 m / 0.000,001 s = 300,000,000 m/s faster than the train – as fast as it always does.
Note that this is a case of either / or. If the speed of light is the same in all frames of references, then we must give up our notions of time. If the light speed depends on your location and speed, then we get to keep our intiutive image of time. So what do the experiments say? All experiments regarding this agree that the speed of light is indeed the same in all frames of references and thus our everyday perception of time is just a first approximation to reality.
Earth’s Magnetic Field
You have been in a magnetic field all your life. The Earth, just like any other planet in the solar system, spawns its own magnetic field. The strength of the field is around B =0.000031 T, but research has shown that this value is far from constant. Earth’s magnetic field is constantly changing. How do we know this? When rocks solidify, they store the strength and direction of the magnetic field. Hence, as long it is possible to figure out the orientation of a rock at the time of solidification, it will tell us what the field was like back then
For rocks that are billions of years old, deducing the original orientation is impossible. Continental drifting has displaced and turned them too often. But thanks to the incredibly low speed of drifting continents, scientists were able to recreate the magnetic field of Earth for the past several million years. This revealed quite a bit.
For one, the poles don’t stand still, but rather wander across the surface with around 50 km per year. The strength of the field varies from practically zero to 0.0001 T (about three times the current strength). And even more astonishingly: the polarity of the field flips every 300,000 years or so. The north pole then turns into the south pole and vice versa. The process of pole reversal takes on average between 1000 and 5000 years, but can also happen within just 100 years. There is no indication that any of these changes had a noticeable impact on plants or animals.
Where does the magnetic field come from? At present there’s no absolute certainty, but the Parker Dynamo Model developed in the sixties seems to be provide the correct answer. The inner core of Earth is a sphere of solid iron that is roughly equal to the Moon in size and about as hot as the surface of the Sun. Surrounding it is the fluid outer core. The strong temperature gradient within the outer core leads to convective currents that contain large amounts of charged particles. According to the theory, the motion of these charges is what spawns the field. Recent numerical simulations on supercomputers have shown that this model is indeed able to reproduce the field in most aspects. It explains the intensity, the dipole structure, the wandering of the poles (including the observed drifting speed) and the pole reversals (including the observed time spans).
It is worth noting that the pole which lies in the geographic north, called the North Magnetic Pole, is actually a magnetic south pole. You might recall that we defined the north pole of a magnet as the pole which will point northwards when the magnet is allowed to turn freely. Since unlike poles attract, this means that there must be a magnetic south pole in the north (talk about confusing). By the same logic we can conclude that the Earth’s South Magnetic Pole is a magnetic north pole.
More interesting physics for non-physicists can be found here:

Physics! In Quantities and Examples
For rocks that are billions of years old, deducing the original orientation is impossible. Continental drifting has displaced and turned them too often. But thanks to the incredibly low speed of drifting continents, scientists were able to recreate the magnetic field of Earth for the past several million years. This revealed quite a bit.
For one, the poles don’t stand still, but rather wander across the surface with around 50 km per year. The strength of the field varies from practically zero to 0.0001 T (about three times the current strength). And even more astonishingly: the polarity of the field flips every 300,000 years or so. The north pole then turns into the south pole and vice versa. The process of pole reversal takes on average between 1000 and 5000 years, but can also happen within just 100 years. There is no indication that any of these changes had a noticeable impact on plants or animals.
Where does the magnetic field come from? At present there’s no absolute certainty, but the Parker Dynamo Model developed in the sixties seems to be provide the correct answer. The inner core of Earth is a sphere of solid iron that is roughly equal to the Moon in size and about as hot as the surface of the Sun. Surrounding it is the fluid outer core. The strong temperature gradient within the outer core leads to convective currents that contain large amounts of charged particles. According to the theory, the motion of these charges is what spawns the field. Recent numerical simulations on supercomputers have shown that this model is indeed able to reproduce the field in most aspects. It explains the intensity, the dipole structure, the wandering of the poles (including the observed drifting speed) and the pole reversals (including the observed time spans).
It is worth noting that the pole which lies in the geographic north, called the North Magnetic Pole, is actually a magnetic south pole. You might recall that we defined the north pole of a magnet as the pole which will point northwards when the magnet is allowed to turn freely. Since unlike poles attract, this means that there must be a magnetic south pole in the north (talk about confusing). By the same logic we can conclude that the Earth’s South Magnetic Pole is a magnetic north pole.
More interesting physics for non-physicists can be found here:

Physics! In Quantities and Examples



