John C. Baez's Blog, page 46

Applied Category Theory at NIST (Part 3)

[image error]

My former student Blake Pollard is working at the National Institute of Standards and Technology. He’s working with Spencer Breiner and Eswaran Subrahmanian, who are big advocates of using category theory to organize design and manufacturing processes. In the spring of 2018 they had a workshop on applied category theory with a lot of honchos from industry and government in attendance—you can see videos by clicking the link.

This spring they’re having another workshop on this topic!

• Applied...

Topos Theory (Part 7)

I’m almost done explaining why any presheaf category is an elementary topos, meaning that

• it has finite colimits;
• it has finite limits;
• it’s cartesian closed.
• it has a subboject classifier.

Last time I explained why such categories are cartesian closed; now let’s talk about the subobject classifier!

Subobject classifiers

In the category of sets, 0-element and 1-element sets play special roles. The 0-element set is the initial object, and any 1-element set is a terminal object. But...

Topos Theory (Part 6)

I’m explaining why any presheaf category is an elementary topos, meaning that

• it has finite colimits;
• it has finite limits;
• it’s cartesian closed.
• it has a subboject classifier.

Last time I tackled the first two bullet points; now let’s do the third. For starters, what’s a cartesian closed category, and why are they so nice? Answering this question will get us into some more ‘philosophical’ aspects of topos theory.

Cartesian closed categories

The category of sets has ‘sums’, also...

The Category Theory Behind UMAP

An interesting situation has arisen. Some people working on applied category theory have been seeking a ‘killer app’: that is, an application of category theory to practical tasks that would be so compelling it would force the world to admit categories are useful. Meanwhile, the UMAP algorithm, based to some extent on category theory, has become very important in genomics:

• Leland McInnes, John Healy and James Melville, UMAP: uniform manifold approximation and projection for dimension...

Superfluid Quasicrystals

Condensed matter physics is so cool! Bounce 4 laser beams off mirrors to make an interference pattern with 8-fold symmetry. Put a Bose–Einstein condensate of potassium atoms into this “optical lattice” and you get a superfluid quasicrystal!

[image error]

You see, no periodic pattern in the plane can have 8-fold symmetry, so the interference pattern of the light is ‘quasiperiodic’: it never repeats itself, thought it comes arbitrarily close, sort of like this pattern drawn by Greg Egan:

[image error]

In the Bose–...

Topos Theory (Part 5)

It’s time to understand why the category of sheaves on a topological space acts like the category of sets in the following ways:

• It has finite colimits.
• It has finite limits.
• It is cartesian closed.
• It has a subboject classifier.

We summarize these four properties by saying the category of sheaves is an elementary topos. (In fact it’s better, since it has all limits and colimits.)

As a warmup, first let’s see why that the category of presheaves on a topological space is an elementary...

Entropy in the Universe

If you click on this picture, you’ll see a zoomable image of the Milky Way with 84 million stars:

But stars contribute only a tiny fraction of the total entropy in the observable Universe. If it’s random information you want, look elsewhere!

First: what’s the ‘observable Universe’, exactly?

The further you look out into the Universe, the further you look back in time. You can’t see through the hot gas from 380,000 years after the Big Bang. That ‘wall of fire’ marks the limits of the...

Topos Theory (Part 4)

In Part 1, I said how to push sheaves forward along a continuous map. Now let’s see how to pull them back! This will set up a pair of adjoint functors with nice properties, called a ‘geometric morphism’.

First recall how we push sheaves forward. I’ll say it more concisely this time. If you have a continuous map 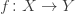between topological spaces, the inverse image of any open set is open, so we get a map

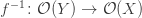
A functor between categories gives a functor between the opposite categories. I’ll use the same...

Topos Theory (Part 3)

Last time I described two viewpoints on sheaves. In the first, a sheaf on a topological space is a special sort of presheaf

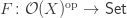
Namely, it’s one obeying the ‘sheaf condition’.

I explained this condition in Part 1, but here’s a slicker way to say it. Suppose 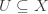is an open set covered by a collection of open sets 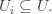Then we get this diagram:

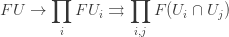
The first arrow comes from restricting elements of 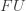to the smaller sets 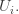The other two arrows come from this: we can either restrict from 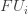to 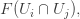or restrict from...

Can We Fix The Air?

A slightly different version of this article I wrote first appeared in Nautilus on November 28, 2019.

Water rushes into Venice’s city council chamber just minutes after the local government rejects measures to combat climate change. Wildfires consume eastern Australia as fire danger soars past “severe” and “extreme” to “catastrophic” in parts of New South Wales. Ice levels in the Chukchi Sea, north of Alaska, hit record lows. England sees floods all across the country. And that’s just this...