Topos Theory (Part 4)

In Part 1, I said how to push sheaves forward along a continuous map. Now let’s see how to pull them back! This will set up a pair of adjoint functors with nice properties, called a ‘geometric morphism’.

First recall how we push sheaves forward. I’ll say it more concisely this time. If you have a continuous map 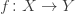between topological spaces, the inverse image of any open set is open, so we get a map

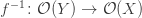
A functor between categories gives a functor between the opposite categories. I’ll use the same...