John C. Baez's Blog, page 14

Mathematics for Climate Change

Some good news! I’m now helping lead a new Fields Institute program on the mathematics of climate change.

You may have heard of the Fields Medal, one of the most prestigious math prizes. But the Fields Institute, in Toronto, holds a lot of meetings on mathematics. So when COVID hit, it was a big problem. The director of the institute, Kumar Murty, decided to steer into the wind and set up a network of institutions working on COVID, including projects on the mathematics of infectious disease ...

Just Intonation (Part 3)

Last time I said a bit about ‘just intonation’: that is, tuning where the most important notes have frequency ratios that are simple fractions. I focused on the historically important case of ‘5-limit tuning’, where the frequency ratios are products of powers of primes ≤ 5.

I went a long way toward getting some popular scales in 5-limit tuning. I started by drawing a chart called a ‘Tonnetz’ where going east multiplies the frequency by 3/2, and going roughly northeast multiplies the frequency ...

Boethius

There’s more to Boethius (480–524 AD) than I knew! Sure, he wrote On the Consolation of Philosophy while imprisoned, later to be executed. And sure, it contains worthy stoic chestnuts like

“Nothing is miserable unless you think it is so; and on the other hand, nothing brings happiness unless you are content with it.”

But how did he get there? In fact his story is quite dramatic. He was born in Rome a few years after the collapse of the Western Roman Empire. After mastering Latin and Gre...

Storm Babet in Granton Harbour

guest post by William Waites

In 2012, before I became involved with Granton Harbour, there was a strong Easterly storm that is still talked about. It washed a number of boats on swinging moorings in the West Harbour onto the shore. Many were badly damaged, some sunk. It was said to be a “30 year storm”. In November 2021, the named storm Arwen put at least two boats on the breakwater and damaged many others. It also finally sunk the yacht Runagate, originally owned by the author Nevil Shute and ...

Just Intonation (Part 2)

Now let’s dive into the beauties of 5-limit tuning—that is, tuning systems with frequency ratios that are products of powers of only the primes 2, 3 and 5:

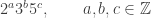
We’ve already tackled 3-limit tuning, where we only got to use the primes 2 and 3. Since multiplying the frequency by 2 merely raises a tone by an octave, giving a tone that sounds ‘just the same, only higher’, we were freed to focus on powers of 3/2. Multiplying the frequency by 3/2 raises a tone by a fifth, so we got a diagram called ...

Just Intonation (Part 1)

In ‘Pythagorean tuning’ all the frequency ratios between tones are products of powers of the primes 2 and 3. I explained this system in detail here. Because the largest prime it uses is 3, we say Pythagorean tuning is a form of ‘3-limit tuning’. One can imagine other forms of 3-limit tuning, though no other is as popular.

Now I want to start talking about ‘5-limit tuning’, where we allow frequency ratios to be products of powers of 2, 3 and 5.

The most popular form of 5-limit tuning is ofte...

Software for Compositional Modeling in Epidemiology

Here is the video of my talk at Applied Category Theory 2023. While it has ‘epidemiology’ in the title, it’s mostly about general ways to use category theory to build flexible, adaptable models:

Here are the slides:

• Software for compositional modeling in epidemiology.

Abstract. Mathematical models of disease are important and widely used, but building and working with these models at scale is challenging. Many epidemiologists use “stock and flow diagrams” to describe ordinary differenti...

Perfect Fifths in Equal Tempered Scales (Part 2)

When I listed some equal-tempered scales with good perfect fifths in Part 1, a reader named Sylvain noticed something interesting. The scales with 5, 7, 12, 29, 41 and 53 tones are particularly good, and

29 = 12 + 12 + 5
41 = 12 + 12 + 12 + 5
53 = 12 + 12 + 12 + 12 + 5

I asked if this is a coincidence. And now I know the answer: no, it’s not! There really is a reason for this pattern.

As we’ll see, part of the reason is that

7/12 ≈ 0.58333333333…

is very close to

log(3/2)/log(2) ≈ 0.58496...

Perfect Fifths in Equal Tempered Scales (Part 1)

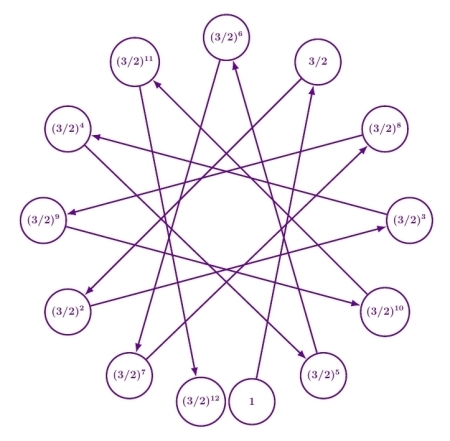
Last time I explained how Pythagorean tuning, one of the older tuning systems, arises from the fact that twelve fifths is almost the same as seven octaves. In other words, multiplying by 3/2 twelve times is almost the same as multiplying by 2 seven times:

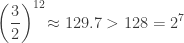
But not quite! That’s why the star above does not quite close.

In the most widely used modern scale, we deal with this discrepancy by using a fifth that does not have a frequency ratio of 3/2, but rather

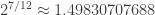
It’s a bit off, but not much. ...

Perfect Fifths in Equal Tempered Scales

Last time I explained how Pythagorean tuning, one of the older tuning systems, arises from the fact that twelve fifths is almost the same as seven octaves. In other words, multiplying by 3/2 twelve times is almost the same as multiplying by 2 seven times:

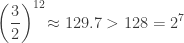
But not quite! That’s why the star above does not quite close.

In the most widely used modern scale, we deal with this discrepancy by using a fifth that does not have a frequency ratio of 3/2, but rather

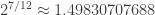
It’s a bit off, but not much. ...