John C. Baez's Blog, page 12

Well Temperaments (Part 2)

Last time I ended with a question: why are certain numbers close to 1 so important in tuning systems? It helps to understand a bit about this before we plunge into the study of well temperaments. It turns out that in some sense western harmony evolved one prime at a time, so let’s look at the subject that way.

The prime 2

If all the frequency ratios in our tuning system were powers of 2:

2i

life would be very simple. Multiplying a frequency by 2 raises its pitch by an octave, so the only ...

Giovanni Battista Doni

You know “do re mi fa sol la ti”? This system for naming notes was invented by a guy named Guido of Arezzo around 1000 AD. But he only named the first 6 notes, because the whole idea of a 7-note scale wasn’t very important for him: instead he used hexachords. And instead of “do” he used “ut”—because these were words in a Latin song.

In the 1600s, a musicologist named Giovanni Battist Doni added the name “si” for the seventh note. And around 1850, Sarah Ann Glover, an English music teache...

Category Theory in Epidemiology

This is a talk I gave at the Edinburgh Mathematical Society on December 4, 2023:

Abstract. “Stock and flow diagrams” are widely used for modeling in epidemiology. Modelers often regard these diagrams as an informal step toward a mathematically rigorous formulation of a model in terms of ordinary differential equations. However, these diagrams have a precise syntax, which can be explicated using category theory. Although commercial tools already exist for drawing these diagrams and solvin...

Well Temperaments (Part 1)

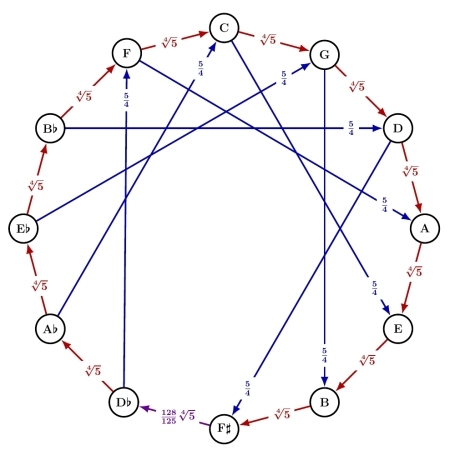
The tuning system called ‘quarter-comma meantone’ dominated western keyboard music from about 1550 to roughly 1690. The reason: it has very nice thirds and fifths in many different keys!

But as I keep saying, every tuning system has problems: like lumps in the carpet, the best you can do is move the problems around. Quarter-comma meantone achieves its greatness by completely flattening out the carpet except for one big lump: a single highly dissonant ‘wolf fifth’. Alas, this utterly spoils k...

The Harmonic Seventh Chord

Traditional western music theory embraces chords with frequency ratios that are products of powers of 2, 3, and 5… but not higher primes. Barbershop quartets go further!

These quartets love four-part harmony using dominant seventh chords. A ‘dominant seventh chord’ contains a note, its major third, its perfect fifth, and its minor seventh. In traditional harmony these have frequencies proportional to 4, 5, 6, and … not 7, because that would be against the rules, but instead some number close t...

Quarter-Comma Meantone (Part 7)

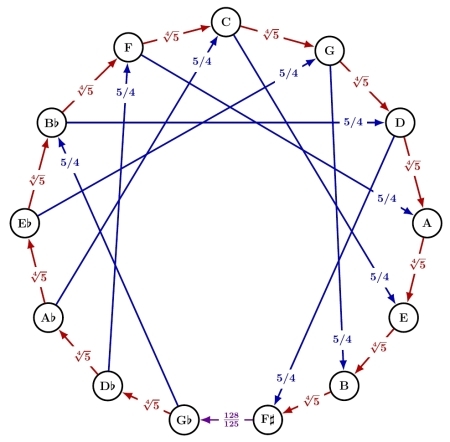
I’ve said a lot about quarter-comma meantone and its great properties. It’s almost time to start exploring the vast realm of ‘well-tempered’ tuning systems that flourished starting around 1690.

But there’s one last thing I want to say about quarter-comma meantone. If you use this system—or any of the systems I’ve talked about except equal temperament—there are some advantages to having your scale start at D rather than C! For example, Wikipedia presents quarter-comma meantone starting from D...

Quarter-Comma Meantone (Part 6)

So far I’ve focused on the quarter-comma meantone system in its mathematically beautiful, symmetrical form above. Today I’ll say more about the scale as actually played: how we trim it down from a 13-note scale to a more practical 12-note scale, and what are the intervals between notes in the resulting scale.

The scale above has:

• a lot of thirds with frequency ratios that are exactly 5/4,

• a lot of fifths that are only slightly flat compared to the ideal 3/2,

• a big problem that we need to...

Quarter-Comma Meantone (Part 5)

I’ve been talking about the quarter-comma meantone tuning system, which dominated western music from about 1550 to 1690. So far I’ve been drawing it using a circle of fifths, as above. This is a diagram where as we go clockwise each note is a fifth higher than the previous one.

But why is this system called ‘meantone’? Briefly, it’s because the size of a whole step between notes in this tuning system—called a ‘tone’—is the geometric mean of the two kinds of whole step in Pythagorean tuning...

Melakarta Ragas

It’s sort of ridiculous that I’ve never studied even the very basics of Indian music, like what are the ragas. Thanks to my friend Todd Trimble I’m dipping my toe into it. And it turns out that in Carnatic music, one of the two main kinds of Indian classical music, the 72 Melakarta ragas are just subsets of the usual 12-tone scale!

I just learned why there are 72. Let’s use western notation and call the 12-tone scale

C D♭ D E♭ E F F♭ G A♭ A B♭ B

To be a Melakarta raga, a subset of these t...

Quarter-Comma Meantone (Part 4)

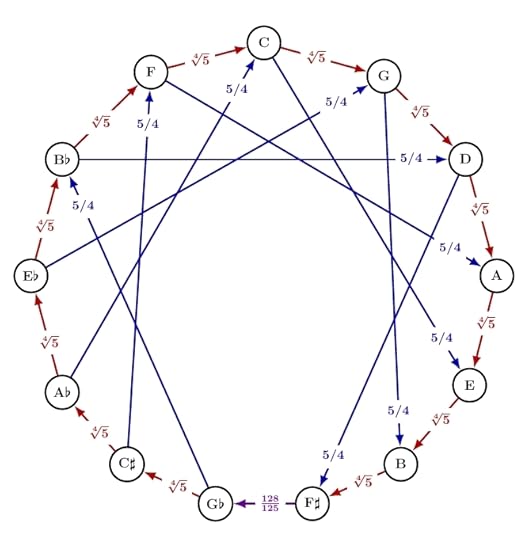
I’ve been talking about the marvelous tuning system that dominated western music from about 1550 to 1690: quarter-comma meantone. Above I’ve drawn it in its most mathematically beautiful form. For convenience I’m drawing it in the key of C, but you could use any key.

This scale has lots of ‘just major thirds’, which are pairs of notes with a frequency ratio of 5/4. I’ve drawn them as dark blue arrows.

This scale also has a visible symmetry under reflection across the vertical axis! What ...