Perfect Fifths in Equal Tempered Scales (Part 1)

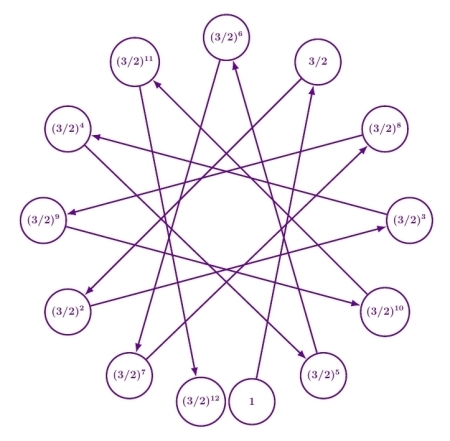
Last time I explained how Pythagorean tuning, one of the older tuning systems, arises from the fact that twelve fifths is almost the same as seven octaves. In other words, multiplying by 3/2 twelve times is almost the same as multiplying by 2 seven times:

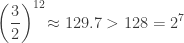
But not quite! That’s why the star above does not quite close.

In the most widely used modern scale, we deal with this discrepancy by using a fifth that does not have a frequency ratio of 3/2, but rather

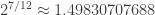
It’s a bit off, but not much. ...