Peter Smith's Blog, page 94

Encore #11: Eine kleine Klein-musik

After three long encores, here’s a short musical interlude for the mathematical which I first linked to in 2008. Fun if you’ve not encountered it before, and still fun to hear again.

Encore #10: Parsons on intuition

Just yesterday, Brian Leiter posted the results of one of his entertaining/instructive online polls, this time on the “Best Anglophone and German Kant scholars  since 1945“. Not really my scene at all. Though I did, back in the day, really love Bennett’s Kant’s Analytic (as philosophy this is surely brilliant, whatever its standing as “scholarship”). I note that in comments after his post, Leiter expresses regret for not having listed Charles Parsons in his list of contributors to Kant scholarship to be voted on. Well, true enough, Parsons has battled over the years to try to make sense of/rescue something from Kantian thoughts about ‘intuition’ as grounding e.g. arithmetical knowledge. But with what success, I do wonder? I found the passages about intuition in Mathematical Thought and Its Objects rather baffling. Here I put together some thoughts from 2008 blog posts.

Is any of our arithmetical knowledge intuitive knowledge, grounded on intuitions of mathematical objects? Parsons writes, “It is hard to see what could make a cognitive relation to objects count as intuition if not some analogy with perception” (p. 144). But how is such an analogy to be developed?

Parsons tries to soften us up for the idea that we can have intuitions of abstracta (where these intuitions are somehow quasi-perceptual) by considering the putative case of perceptions – or are they intuitions? – of abstract types such as letters. The claim is that “the talk of perception of types is something normal and everyday” (p. 159).

But it is of course not enough to remark that we talk of e.g. seeing types: we need to argue that we can take our talk here as indeed reporting a (quasi)-perceptual relation to types. Well, here I am, looking at a squiggle on paper: I immediately see it as being, for example, a Greek letter phi. And we might well say: I see the letter phi written here. But, in this case, it might well be said, ‘perception of the type’ is surely a matter of perceiving the squiggle as a token of the type, i.e. perceiving the squiggle and taking it as a phi.

Now, it would be wrong to suppose that – at an experiential level – ‘seeing as’ just factors into a perception and the superadded exercise of a concept or of a recognitional ability. When the aspect changes, and I see the lines in a drawing as a picture of a duck rather than a rabbit, at some level the content of my conscious perception itself, the way it is articulated, changes. Still, in seeing the lines as a duck, it isn’t that there is more epistemic input than is given by sight (visual engagement with a humdrum object, the lines) together with the exercise of a concept or of a recognitional ability. Similarly, seeing the squiggle as a token of the Greek letter phi again doesn’t require me to have some epistemic source over and above ordinary sight and conceptual/recognitional abilities. There is no need, it seems, to postulate something further going on, i.e. quasi-perceptual ‘intuition’ of the type.

The deflationist idea, then, is that seeing the type phi instantiated on the page is a matter of seeing the written squiggle as a phi, and this involves bring to bear the concept of an instance of phi. And, the suggestion continues, having such a concept is not to be explained in terms of a quasi-perceptual cognitive relation with an abstract object, the type. If anything it goes the other way about: ‘intuitive knowledge of types’ is to be explained in terms of our conceptual capacities, and is not a further epistemic source. (But note, the deflationist who resists the stronger idea of intuition as a distinctive epistemic source isn’t barred from taking Parsons’s permissive line on objects, and can still allow the introduction of talk via abstraction principles of abstract objects such as types. He needn’t have a nominalist horror of talk of abstracta.)

Let’s be clear here. It may well be that, as a matter of the workings of our cognitive psychology, we recognize a squiggle as a token phi by comparing it with some stored template. But that of course does not imply that we need be able, at the personal level, to bring the template to consciousness: and even if we were to have some quasi-perceptual access to the template itself, it wouldn’t follow that we have quasi-perceptual access to the type. Templates are mental representations, not the abstracta represented.

Parsons, however, explicitly rejects the sketched deflationary story about our intuition of types when he turns to consider the particular case of the perception of expressions from a very simple ‘language’, containing just one primitive symbol ‘|’ (call it ‘stroke’), which can be concatenated. The deflationary reading

does not accurately render our perceptual consciousness of strokes. It would make what I want to call intuition of a string an instance of seeing a certain inscription as  of a type …. But in actual cases, the identification of the type will be firmer and more explicit that the identification of any physical inscriptions that is an instance of the type. That the inscriptions are real physical objects with definite physical properties plays no role in the mathematical treatment of the language, which is what concerns us. An illusory presentation of a string, provided it is sufficiently clear, will do as well to illustrate a mathematical notion as a real one. (p. 161)

There seem to be two points here, neither of which will really trouble the deflationist.

The first point is that the identification of a squiggle’s type may be “firmer and more explicit” than our determination of its physical properties as a token (which I suppose means that a somewhat blurry shape may still definitely be a letter phi). But so what? Suppose we have some discrete conceptual pigeon-holes, and have reason to take what we see as belonging in one pigeonhole or another (as when we are reading Greek script, primed with the thought that what we are seeing will be a sequence of letters from forty eight upper and lower case possibilities). Then fuzzy tokens can get sharply pigeonholed. But there’s nothing here that the deflationist about seeing types can’t accommodate.

The second point is that, for certain illustrative purposes, illusory strings are as good as physical strings. But again, so what? Why shouldn’t seeing an illusory strokes as a string be a matter of our tricked perceptual apparatus engaging with our conceptual and/or /recognitional abilities? Again, there is certainly no need to postulate some further cognitive achievement, ‘intuition of a type’.

Oddly, Parsons himself, when wrestling with issues about vagueness, comes close to making these very points. For you might initially worry that intuitions which are founded in perceptions and imaginings will inherit the vagueness of those perceptions or imaginings – and how would that then square the idea that mathematical intuition latches onto sharply delineated objects? But Parsons moves to block the worry, using the example of seeing letters again. His thought now seems to be the one above, that we have some discrete conceptual pigeon-holes, and in seeing squiggles as a phi or a psi (say), we are pigeon-holing them. And the fact that some squiggles might be borderline candidates for putting in this or that pigeon-hole doesn’t (so to speak) make the pigeon-holes less sharply delineated. Well, fair enough. But thinking in these terms surely does not sustain the idea that we need some basic notion of the intuition of the type phi to explain our pigeon-holing capacities.

So, I’m unpersuaded that we actually need (or indeed can make much sense of) any notion of the quasi-perceptual ‘intuition of types’ – and in particular, any notion of the intuition of types of stroke-strings – that resists a deflationary reading. But let’s suppose for a moment that we follow Parsons and think we can make sense of such a notion. Then what use does he want to make of the idea of intuiting strokes and stroke-strings?

Parsons writes

What is distinctive of intuitions of types [here, types of stroke-strings] is that the perceptions and imaginings that found them play a paradigmatic role. It is through this that intuition of a type can give rise to propositional knowledge about the type, an instance of intuition that. I will in these cases use the term ‘intuitive knowledge’. A simple case is singular propositions about types, such as that ||| is the successor of ||. We see this to be true on the basis of a single intuition, but of course in its implications for tokens it is a general proposition. (p. 162)

This passage raises a couple of issues worth commenting on.

One issue concerns the claim that there is a ‘single intuition’ here on basis of which we see that that ||| is the successor of ||. Well, I can think of a few cognitive situations which we might agree to describe as grounding quasi-perceptual knowledge that ||| is the successor of || (even if some of us would want to give a deflationary construal of the cases, one which doesn’t appeal to intuition of abstracta). For example,

We perceive two stroke-strings
       ||
       |||
and aligning the two, we judge one to be the successor or the other.
We perceive a single sequence of three strokes ||| and flip to and fro between seeing it as a threesome and as a block of two followed by an extra stroke.

But, even going along with Parsons on intuition, neither of those cases seems aptly described as seeing something to be true on the basis of a single intuition. In the first case, don’t we have an intuition of ||| and a separate intuition of || plus a recognition of the relation between them? In the second case, don’t we have successive intuitions, and again a recognition of the relation between them? It seems that our knowledge that ||| is the successor of || is in either case grounded on intuitions, plural, plus a judgement about their relation. And now the suspicion is that it is the thoughts about the relations that really do the essential grounding of knowledge here (thoughts that could as well be engaging with perceived real tokens or with imagined tokens, rather than with putative Parsonian intuitions that, as it were, reach past the real or imagined inscriptions to the abstracta).

The other issue raised by the quoted passage concerns the way that the notion of ‘intuitive knowledge’ is introduced here, as the notion of propositional knowledge that arises in a very direct and non-inferential way from intuition(s) of the objects the knowledge is about: “an item of intuitive knowledge would be something that can be ‘seen’ to be true on the basis of intuiting objects that it is about” (p. 171). Such a notion looks very restrictive – on the face of it, there won’t be much intuitive knowledge to be had.

But Parsons later wants to extend the notion in two ways. First

Evidently, at least some simple, general propositions about strings can be seen to be true. I will argue that in at least some important cases of this kind, the correct description involves imagining arbitrary strings. Thus, that will be included in ‘intuiting objects that a proposition is about’. (p. 171)

But even if we now allow intuition of ‘arbitrary objects’, that still would seem to leave intuitive knowledge essentially non-inferential. However,

I do not wish to argue that the term ‘intuitive knowledge’ should not be used in that [restrictive] way. Our sense, following that of the Hilbert School, is a more extended one that allows that certain inferences preserve intuitive knowledge, so that there can actually be a developed body of mathematics that counts as intuitively known. This seems to me a more interesting conception, in addition to its historical significance. Once one has adopted this conception, one has to consider case by case what inferences preserve intuitive knowledge. (p. 172)

Two comments about his. Take the second proposed extension first. The obvious question to ask is: what will constrain our case-by-case considerations of which kinds of inference preserve intuitive knowledge? To repeat, the concept of intuitive knowledge was introduced by reference to an example of knowledge seemingly non-inferentially obtained. So how are we supposed to ‘carry on’, applying the concept now to inferential cases? It seems that nothing in our original way of introducing the concept tells us which such further applications are legitimate, and which aren’t. But there must be some constraints here if our case-by-case examinations are not just to involve arbitrary decisions. So what are these constraints? I struggle to find any clear explanation in Parsons.

And what about intuiting ‘arbitrary’ strings? How does this ground, for example, the knowledge that every string has a successor? Well, supposedly, (1) “If we imagine any [particular] string of strokes, it is immediately apparent that a new stroke can be added.” (p. 173) (2) But we can “leave inexplicit its articulation into single strokes” (p. 173), so we are imagining an arbitrary string, and it is evident that a new stroke can be added to this too. (3) “However, …it is clear that the kind of thought experiments I have been describing can be taken as intuitive verifications of such statements as that any string of strokes can be extended only if one carries them out on the basis of specific concepts, such as that of a string of strokes. If that were not so, they would not confer any generality.” (p. 174) (4) “Although intuition yields one essential element of the idea that there are, at least potentially, infinitely many strings …more is involved in the idea, in particular that the operation of adding an additional stroke can be indefinitely iterated. The sense, if any, in which intuition tells us that is not obvious.” (p. 176) But (5) “Once one has seen that every string can be extended, it is still another question whether the string resulting by adding another symbol is a different string from the original one. For this it must be of a different type, and it is not obvious why this must be the case. … Although it will follow from considerations advanced in Chapter 7 that it is intuitively known that every string can be extended by one of a different type, ideas connected with induction are needed to see it” (p. 178).

There’s a lot to be said about all that, though (4) and (5) already indicate that Parsons thinks that, by itself, ‘intuition’ of stroke-strings might not take us terribly far. But does it take us even as far as Parsons says? For surely it is not the case that imagining/intuiting adding a stroke to an inexplicitly articulated string, together with the exercise of the concept of a string of strokes, suffices to give us the idea that any string can be extended. For we can surely conceive of a particularist reasoner, who has the concept of a string, can bring various arrays (more or less explicitly articulated) under that concept, and given a string can recognize that this one can be extended – but who can’t advance to frame the thought that they can all be extended? The generalizing move surely requires a further thought, not given in intuition.

Indeed, we might now wonder quite what the notion of intuition is doing here at all. For note that (1) and (2) are a claims about what is imaginable. But if we can get to general results about extensibility by imagining particular strings (or at any rate, imagining strings “leaving inexplicit their articulation into single strokes”, thus perhaps ||…|| with a blurry filling) and then bring them under concepts and generalizing, why do we also need to think in terms of having cognitive access to something else which is intrinsically general, i.e. stroke-string types? It seems that Parsonian intuitions actually drop out of the picture. What gives them an essential role in the story?

Finally, note Parsons’s pointer forward to the claim that ideas “connected with induction” can still be involved in what is ‘intuitively known”. We might well wonder again as we did before: what integrity is left to the notion of intuitive knowledge once it is no longer tightly coupled with the idea of some quasi-perceptual source and allows inference, now even non-logical inference, to preserve intuitive knowledge? I can’t wrestle with this issue further here: but Parsons ensuing discussion of these matters left me puzzled and unpersuaded.

Again, as with the last post, that’s how things seemed to be more than seven years ago. If other readers have a better of sense of what a Parsonian line on intuition might come to, comments are open!

Encore #9: Parsons on noneliminative structuralism

I could post a few more encores from my often rather rude blog posts about Murray and Rea’s Introduction to the Philosophy of Religion. But perhaps it would be better for our souls to to an altogether more serious book which I blogged about at length, Charles Parsons’ Mathematical Thought and Its Objects. I got a great deal from trying to think through my reactions to this dense book in 2008. But I often struggled to work out what was going on. Here, in summary, is where I got to in a series of posts about the book’s exploration of structuralism. I’m very sympathetic to structuralist ideas: but I found it difficult to pin down Parsons’s version.

In his first chapter, Parsons defends a thin, logical, conception of ‘objects’ on which “Speaking of objects just is using the linguistic devices of singular terms, predication, identity and quantiÞcation to make serious statements” (p. 10). His second chapter critically discusses eliminative structuralism. The third chapter presses objections against modal structuralism. But Parsons still finds himself wanting to say that “something close to the structuralist view is true” (p. 42), and he now moves on characterize his own preferred noneliminative version. We’ll concentrate on the view as applied to arithmetic.

Parsons makes two key initial points. (1) Unlike the eliminative structuralist, the noneliminativist “take[s] the language of mathematics at face value” (p. 100). So arithmetic is indeed about numbers as objects. What characterizes the position as structuralist is that we don’t “take more as objectively determined about the objects about which it speaks than [the relevant mathematical] language itself specifies” (p. 100). (2) Then there is “the aspect of the structuralist view stressed by Bernays, that existence for mathematical objects is in the context of a background structure” (p. 101). Further, structures aren’t themselves objects, and “[the noneliminativist] structuralist account of a particular kind of mathematical object does not view statements about that kind of object as about structures at all”.

But note, thus far there’s nothing in (1) and (2) that the neo-Fregean Platonist (for example) need dissent from. The neo-Fregean can agree e.g. that numbers only have numerical intrinsic properties (pace Frege himself, even raising the Julius Caesar problem is a kind of mistake). Moreover, he can insist that individual numbers don’t come (so to speak) separately, one at a time, but come all together forming an intrinsically order structured — so in, identifying the number 42 as such, we necessarily give its position in relation to other numbers.

So what more is Parsons saying about numbers that distinguishes his position from the neo-Fregean? Well, he in fact explicitly compares his favoured structuralism with the view that the natural numbers are sui generis in the sort of way that the neo-Fregean holds. He writes

One further step that the structuralist view takes is to reject the demand for any further story about what objects the natural numbers are [or are not]. (p. 101)

The picture seems to be that the neo-Fregean offers a “further story” at least in negatively insisting that numbers are sui generis, while the structuralist refuses to give such a story. As Parsons puts it elsewhere

If what the numbers are is determined only by the structure of numbers, it should not be part of the nature of numbers that none of them is identical to an object given independently.

But of course, neo-Fregeans like Hale and Wright won’t agree that their rejection of cross-type identities is somehow an optional extra: they offer arguments which — successfully or otherwise — aim to block the Julius Caesar problem and reveal certain questions about cross-type identifications as ruled out by our very grasp of the content of number talk. So from this neo-Fregean perspective, we can’t just wish into existence a coherent structuralist position that both (a) construes our arithmetical talk at face value, as referring to numbers as genuine objects, yet also (b) insists that the possibility of cross-type identifications is left open, because — so this neo-Fregean story goes — a properly worked out version of (a), together with reflection on the ways that genuine objects are identified under sortals, implies that we can’t allow (b).

Now, on the sui generis view about numbers, claims identifying numbers with sets will be ruled out as plain false. Or perhaps it is even worse, and such claims fail to make the grade for being either true or false (though it is, of course, notoriously difficult to sustain a stable, well-motivated, distinction between the neither-true-nor-false and the plain false — so let’s not dwell on this). Conversely, assuming that numbers are objects, if claims identifying them with sets and the like are false or worse, then numbers are sui generis. So it seems that if Parsons is going to say that numbers are objects but are not sui generis, he must allow space for saying that claims identifying numbers with sets (or if not sets, at least some other objects) are true. But then Parsons is faced with the familiar Benacerraf multiple-candidates problem (if not for sets, then presumably an analogous problem for other candidate objects, whatever they are: let’s keep things simple by running the argument in the familiar set-theoretic setting). How do we choose e.g. between saying that the finite von Neumann ordinals are the natural numbers and saying that the finite Zermelo ordinals are?

It seems arbitrary to plump for either choice. Rejecting both together (and other choices, on similar grounds) just takes us back to the sui generis view — or even to Benacerraf’s preferred view that numbers aren’t objects at all. So that, it seems, leaves just one position open to Parsons, namely to embrace both choices, and to avoid the apparently inevitable absurdity that 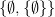is identical to 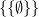(because both are identical to 2) by going contextual. It’s only in one context that ‘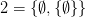’ is true; and only in another that ‘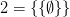’ is true.

And this does seem to be the line Parsons seems inclined to take: “The view we have defended implies that [numbers] are not definite objects, in that the reference of terms such as ‘the natural number two’ is not invariant over all contexts” (p. 106). But how are we to understand that? Is it supposed to be rather like the case where, when Brummidge United is salient, ‘the goal keeper’ refers to Joe Doe, but when Smoketown City is salient, ‘the goal keeper’ refers to Richard Roe? So when the von Neumann ordinals are salient, ‘2’ refers to 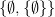and the Zermelo ordinals are salient, ‘2’ refers to 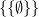? But then, to pursue the analogy, while ‘the goal keeper’ is indeed sometimes used to talk about now this particular role-filler and now that one, the designator is apparently also sometimes used more abstractly to talk about the role itself — as when we say that only the goal keeper is allowed to handle the ball. Likewise, even if we do grant that ‘2’ sometimes refers to role-fillers, it seems that sometimes it is used to talk more abstractly about the role — perhaps as when we say, when no particular -sequence of sets is salient, that 2 is the successor of the successor of zero. Well, is this the way Parsons is inclined to go, i.e. towards a structuralism developed in terms of a metaphysics of roles and role-fillers?

Well, Parsons does explicitly talk of “the conclusion that natural numbers are in the end roles rather than objects with a definite identity” (p. 105). But why aren’t roles objects after all, in his official thin ‘logical’ sense of object? — for we can use “the linguistic devices of singular terms, predication, identity and quantification to make serious statements” about roles (and yes, we surely can make claims about identity and non-identity: the goal keeper is not the striker). True, roles are as Parsons might say, “thin” or “impoverished” objects whose intrinsic properties are determined by their place in a structure. But note, Parsons’s official view about objects didn’t require any sort of ‘thickness’: indeed, he is “most concerned to reject the idea that we don’t have genuine reference to objects if the ‘objects’ are impoverished in the way in which elements of mathematical structures appear to be” (p. 107). And being merely ‘thin’ objects, roles themselves (e.g. numbers) can’t be the same things as ‘thick’ role-fillers. So now, after all, numbers qua number-roles do look to be sui generis entities with their own identity — objects, in the broad logical sense, which are not to be identified with any role-filler — in other words, just the kind of thing that Parsons seems not to want to be committed to.

The situation is further complicated when Parsons briefly discusses Dedekind abstraction, though similar issues arise. To explain: suppose we have a variety of ‘concrete’ structures, whether physically realized or realized in the universe of sets, that satisfy the conditions for being a simply infinite system. Then Dedekind’s idea is that we ‘abstract’ from these a further structure 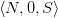which is — so to speak — a ‘bare’ simply infinite system without other inessential physical or set-theoretic features, and it is elements of this system which are the numbers themselves. (Erich H. Reck nicely puts it like this: “[W]hat is the system of natural numbers now? It is that simple infinity whose objects only have arithmetic properties, not any of the additional, ‘foreign’ properties objects in other simple infinities have.”) Since the bare structure is all that is generated by the Dedekind abstraction, “it conforms to the basic structuralist intuition in that the number terms introduced do not give us more than the structure” (p. 105), to borrow Parsons’s words. But, he continues,

This procedure gets its force from the use of a typed language. Thus, the question arises what is to prevent us from later, for some specific purpose, speaking of numbers in a first-order language and even affirming identities of numbers and objects given otherwise.

To which the answer surely is that, to repeat, on the Dedekind abstraction view, the ‘thin’ numbers determinately do not have intrinsic properties other than those given in the abstraction procedure which introduces them: so, by assumption, they are determinately distinct from any ‘thicker’ object with such further properties. Why not?

So now I’m puzzled. For Parsons, does ‘the natural number two’ (i) have a fixed reference to a sui-generis ‘thin’ role-object (or Dedekind abstraction, if that’s different), or (ii) have a contextually shifting reference to a role-filler, or (iii) both? The latter is perhaps the most charitable reading. But it would have helped a lot if Parsons had much more explicitly related his position to an articulated metaphysics of role/role-filler structuralism. Elsewhere, he writes that “the metaphysical tradition is likely to be misleading as a source of ideas about the objects of modern mathematics”. Maybe that’s right. But then it is all the more important to be absolutely clear and explicit about what new view is being proposed. And here, I fear, Parsons’s writing falls short of that.

Or so I thought now over seven years ago. I haven’t re-read Parsons’s text since. I would be very interested to get any comments from readers who worked their way to some  clearer understanding of his position. 

Encore #8: Perhaps not the strongest argument ever?

For some reason that now escapes me, I found myself in early 2008 reading An Introduction to the Philosophy of Religion by Michael Murray and Michael Rea (published by CUP in the same wide-ranging series as my Gödel book). I can’t say that I much rated the book. Partly that’s because it seemed to have little to do with the religion of most ordinary church-goers; and partly because many of the arguments seemed dreadful, to use a technical term. I was particular entranced by this one:

Philosophy of Religion 4: Lord, Liar, Lunatic (March 30, 2008)

Pp. 75–80 of the Murray/Rea Introduction contain a rather extraordinary episode which I can’t forbear from commenting on.

They consider the following argument — they call it the “Lord-Liar-Lunatic” argument — for believing the Jesus of Nazereth was divine. Jesus claimed to be divine. The claim is either true or false. If the latter, either Jesus knew it was false, and was a liar. “On the other hand, if he unwittingly falsely claimed to be divine, then he was crazy.” But

the influence of Jesus’s teaching … has been enormous. Literally millions of people have found peace, sanity and virtue in orienting their lives round his teachings. … All of these facts together make it seem very likely that Jesus was neither so wicked and egomaniacal as to try deliberately to deceive others into thinking that he was divine, nor so mentally unbalanced as to be fundamentally confused about his own origin, powers and identity. If Jesus was not a liar or a lunatic … then there is only one alternative left: his claim to divinity was true.

Which really is a quite jaw-droppingly awful argument. Suppose we grant that Jesus claimed himself to be fully divine (I thought that was actually contended by some biblical scholars, but let it pass). And suppose he did so fully sincerely even though he wasn’t divine. Then he was indeed badly deluded. But what on earth is the problem with that? History is full of people suffering from some “crazy” delusions yet functioning very successful in other domains of life.

Murray and Rea assume that you can’t be so badly off beam as to believe yourself divine when you aren’t and still count as fully sane: it isn’t, they argue, the sort of thing you can make a straight mistake about, at least if “divine” is used in the “perfect being” sense. OK: let’s agree with Murray and Rea: if Jesus was not divine, but believed he was, then he was not fully “sane”. But — to repeat — of course delusions of various kinds are entirely compatible with functioning successfully in all sorts of ways: being a great painter or architect, say, or being a great mathematician or chess player, surely. And why not be being an inspirational moral teacher? Bad cognitive mulfunction in one area is compatible with managing spectacularly well in other areas: indeed (who knows?) it could even contribute to the successes.

Imagine a world of many messianic preachers, some indeed deluded as to their own divinity (well, there’s been a fair bit of it around over the centuries — it’s a mental virus that can infect people, it seems). Most preach a variety of messages that fall on stony ground. Some preach messages that “catch on” temporarily, but in a quite horribly destructive way. But  let’s suppose that, picking up on ideas already in the air, one charismatically preaches in a way that strikes a chord with his contemporary listeners; the message is taken up, embroidered, mixed in with other themes his followers, and propagated; and this time, let’s suppose “millions of people [find] peace, sanity and virtue in orienting their lives round [these precipitations of] his teachings”. But the fact that one such preacher happens to initiate a benignly propagating message [if that’s what we think Christianity is — of course, that’s the subject of a different argument!] isn’t any evidence at all that the originator’s pretensions to be divine are any less deluded that those of his less successful colleagues. Given enough different shots at it, and given  our apparent human propensities to be caught up by religious ideas, some deluded preachers were more or less bound to strike lucky.

Murray and Rea write that “the Lord-Liar-Lunatic argument seems to us … to be stronger than some contemporary critics have given it credit for being”. I do find that an astonishing thing to say. The argument is quite transparently hopeless.

And it still strikes me as transparently hopeless despite some of the comments the original posting received!

Encore #7: Postcards from Siena

Continuing the series of re-posts as we approach the tenth birthday of the blog. In the early years of the blog, The Daughter had a home near Siena, and we visited often, and got to love the place. The photo above is her village a few miles east of Siena (and indeed the just-visible white blob in the centre of the picture, is the dome of the Duomo, which was covered for repair at the time). Here are some snippets from one visit in May and June 2008.

We have decamped back to Siena for the better part of a month. Or rather to a small village about 15km to the east. Siena is already bustling with tourists, but here things are very quiet. From one window, a few domestic sounds of village life; from another I can see half-a-dozen men slowly working in a line between the vines below the village walls. I suspect that logic postings here might be infrequent for a while, though I’ve brought a laptop and some things to work on when the mood takes me.

In the little piazza beneath our window, children have been celebrating their first communion. Being Italy, the occasion is marked before and after by a lot of noise, clanging bells and a brass band, and the inevitable gathering for food and wine. There are proud parents and grandparents, and the youth of the village dressed more for a party than for a solemn occasion. No doubt, it all means different things to different people: but these occasions are just part of village life, and I suspect that many of the participants are just comfortable through long familiarity with participating in religious services (with more or less regularity, more or less enthusiasm), and don’t worry too much about what it all means. It is what you do, and it ceremoniously links the occasions of life with the eternal verities.

We normally never watch breakfast TV, but here we have the excuse of trying to pick up more Italian: and actually it isn’t at all bad. The weekend show we watch has a nice slot visiting different places around Italy and talking at length about their local produce, and demonstrating a characteristic recipe. That — followed by walking through the woods onto the estate of Villa Arceno and alongside their vineyards — worked up appetites for Sunday lunch at a favourite restaurant, La Bottega di Lornano. But by then the weather was getting too threatening again to eat outside (even under their big awning). Still, a terrific meal as always, in Tuscan quantities, and we drank a favourite wine, Dievole’s Broccato. Prices in Italy are going up, and the pound is going down against the euro, so this is not quite the stunning bargain it would have seemed three years ago. But we still ate much better for less than the cost of a second-rate chain restaurant meal in England. Which is why we very rarely bother to eat out at home.

We went yesterday to the Archivio di Stato in Siena (which does guided visits three times a morning). The interest there — apart from the great ranks of volumes of documents — is an exhibition of the Tavolette di Biccherna. These are painted wooden panels that were produced as covers for bundles of civic account books, starting in 1258 with the practice continuing to the eighteenth century. The earlier ones, in particular, are fascinating (particularly interesting to see secular art of the time). Very definitely worth a visit: we enjoyed it great deal. There were exactly two other people there when we went.

Here, everyone has to park outside the walls of the old part of the borgo. But that’s no hardship. There’s stone and gravel put down between the olive trees just under the house, and you park the car among them, leaving it to quietly admire the views for miles over the hills. The trees have been brutalized since last year, obviously scaring the living daylight out of them, and as a result they are beginning to fruit like mad. I can report that the local olive oils vary, but from merely very good indeed to the amazing. (And judging from the ages on the gravestones in the village cemetery, they must have magically life-extending properties.)

It’s sunnier and warmer (for a while). This year the excellent restaurant just a few steps across the piazza has put a few tables outside, and will bring you a coffee and cornetto from when they open up in the morning, or an aperitivo in the afternoon. A great idea, but so far the weather has been such that we’ve only made use of it a few times. But this morning, sitting in the sun at half-past nine, it was already pretty hot. At last.

The meteo predicts that really good weather will start on Thursday. Since we are leaving on Wednesday, this is just a bit galling. This morning it was so cold we put the heating on again. And jazz last night in the little village piazza under our window was good, but not the balmy June night under the stars we might have expected, and the well-wrapped-up audience was understandably a bit thin.

Siena itself is like Cambridge at least in this respect: the tourists tend to stick to a small part of the city. So it can be very busy round the Campo and the Duomo. But other sights, even those the guide books warmly praise, can be more or less deserted. We did make one nice discovery a couple of days ago when it was dry in the afternoon. We found ourselves at the botanical gardens which we’d never visited before (and, predictably, they were more or less empty of people). They are very fine, cool under the trees, tumble down a steep slope, and so the views out of the city are beautiful. Recommended.

CD choice #3

I have been listening and re-listening over the last week to Angela Hewitt’s new CD of sixteen Scarlatti sonatas. An experience I most certainly can recommend. She plays, as always, with such thought, precision, polish, articulation, sheer musicality. Some pieces Hewitt plays surprisingly slowly, including the final one, the very familiar Kk 380: but her typically fascinating musical notes in the CD booklet make her case for thinking, with Kirkpatrick, that Scarlatti’s tempo indications are more indications of rhythmic character than speed. Listening to Hewitt’s disc, though, took me back to listen yet again to Mikhail Pletnev’s 1995 double CD. When I first found this shortly after it was released it was completely revelatory (to someone who only knew some of these sonatas from harpsichord performances). Pletnev is even freer, even more pianistic, than Hewitt; I suppose interesting questions arise about performances as distant from historic, period, style as this. But the results are so beguiling — often poignant, strange, emotionally telling — that I have to keep returning to them.

More categorial gentleness …

A new version of the Gentle Introduction to Category Theory (version of Feb 8th, pp. x + 273) is now online. Get it (by preference) from my academia.edu page or alternatively download it from the categories page here. Nearly all the sections from the old Notes on Category Theory have now been woven into the much re-arranged Gentle Intro — though for the last three chapters, the inclusion is just by the brute-force method of cutting’n’pasting from the old Notes without revision! Anyway, I have now taken the old Notes off-line and hereby cheerfully repudiate them as, erm, juvenilia. So to speak.

I’m still very much trying to nail down some of the basic categorial technicalities to my own satisfaction, aiming to make them seems as “obvious” as I can. In due course, there should be more episodes of discursive chat; and there is quite a bit more technical material I want to cover too. But I hope that even in its rather unpolished and very incomplete state, the Gentle Intro will be useful to those who would like something which is perhaps, in various respects, a bit more accessible(?) than e.g. Awodey’s or Leinster’s fine books.

Apple nerd note: Duet Display

If you have e.g. a MacBook of some description (or indeed a Windows machine), and an iPad, you can use the iPad as an additional display. Duet Display works over a USB cable, so is much much smoother and less flakey in operation than old implementations of the general idea using Bluetooth. Works a treat. OK, it won’t magically increase your “productivity” but it assuredly reduces the irritations of window-juggling when working. You can get Duet Display on the app store or from their site. If you don’t know it, a warmly recommended bargain.

Encore #6: Gödel vs Turing

And from the same collection of articles, a link to a paper that I (for once!) unreservedly praised and agreed with.

Church’s Thesis 13: Gödel on Turing (June 14, 2007)

Phew! At last, I can warmly recommend another paper in Church’s Thesis after 70 Years …

Some headline background: Although initially Gödel was hesitant, by about 1938 he is praising Turing’s work as establishing the “correct definition” of computability. Yet in 1972 he writes a short paper on undecidability, which includes a section headed “A philosophical error in Turing’s work”.

So an issue arises. Has Gödel changed his mind?

Surely not. What Gödel was praising in 1938 was Turing’s analysis of a finite step-by-step computational procedure. (Recall the context: Turing was originally fired up by the Entscheidungsproblem, which is precisely the question whether there is a finitistic procedure that can be mechanically applied to decide whether a sentence is a first-order logical theorem. So it is analysis of such procedures that is called for, and that was of concern to Gödel too.)

What the later Gödel was resisting in 1972 was Turing’s further thought that, in the final analysis, human mental procedures cannot go beyond such finite mechanical procedures. Gödel was inclined to think that, in the words of his Gibbs Lecture, the human mind “infinitely surpasses the powers of any finite machine”. So, surely, there is no change of mind, just an important change of topic.

That’s at any rate what I have previously taken to be the natural view. But I confess I’d never done any careful homework to support it. Perhaps because it chimes with view I’ve been at pains to stress in various comments on this collection of articles — namely that there is a very important distinction between (1)  the “classic” Church-Turing thesis that the effectively computable functions (step-by-small-step algorithmically computable functions) are exactly the recursive functions, and (2)  various bolder theses about what can be computed by (idealised) machines and/or by minds.

And so it is very good to see that now Oron Shagrir has given a careful and convincing defence of this natural view of Gödel’s thoughts on Turing, with lots of detailed references, in his (freely downloadable!) paper “Gödel on Turing on computability”. Good stuff!

Encore #5: Church’s Thesis and open texture

At various times, I have blogged a series of posts as I read through a book, often en route to writing a review. One of first books to get this treatment was  the collection of articles Church’s Thesis After 70 Years edited by Adam Olszewski et al. This was a very mixed bag, as is often the way with such collections. But some pieces stood out as worth thinking about. Here’s one (which I initially posted about in 2007, but returned to a bit later when we read it one Thursday in the Logic Seminar.

Stewart Shapiro, “Computability, Proof, and Open-Texture” (January 18, 2008)

Let me say straight away that it is a very nice paper, written with Stewart Shapiro’s characteristic clarity and good sense.

Leaving aside all considerations about physical computability, there are at least three ideas in play in the vicinity of the Church-Turing Thesis. Or betters there is first a cluster of inchoate, informal, open-ended, vaguely circumscribed ideas of computability, shaped by some paradigm examples of everyday computational exercises. Then second there is the semi-technical idea of effective computability (with quite a carefully circumscribed though still informal definition, as given in various texts, such as Hartley Rogers’ classic). Then thirdly there is the idea of Turing computability (and along with that, of course, the other provability equivalent characterizations of computability as recursiveness, etc.).

It will be agreed on all sides that our original inchoate, informal, open-ended ideas could and can be sharpened up in various ways. Hence, the notion of effective computability takes some strands in inchoate notion and refines and radically idealizes them in certain ways (e.g. by abstracting from practical considerations of the amount of time or memory resources a computation would use). But there are other notions, e.g. of feasible computability, that can also be distilled out. Or notions of what is computable by a physically realisable set-up in this or other worlds. It isn’t that the notion of effective computability is — so to speak — the only clear concept waiting to be revealed as the initial fog clears.

So I think that Shapiro’s rather Lakatosian comments in his paper about how concepts get refined and developed and sharpened in mathematical practice are all well-taken, as comments about how we get from our initial inchoate preformal ideas to, in particular, the semi-technical notion of effective computability. And yes, I agree, it is important to emphasize is that we do indeed need to do some significant pre-processing of our initial inchoate notion of computability before we arrive at a notion, effective computability, that can reasonably be asserted to be co-extensive with Turing computability. After all, ‘computable’ means, roughly, ‘can be computed’: but ‘can’ relative to what constraints? Is the Ackermann function computable (even though for small arguments its value has more digits than particles in the known universe)? Our agreed judgements about elementary examples of common-or-garden computation don’t settle the answer to exotic questions like that. And there is an element of decision — guided of course by the desire for interesting, fruitful concepts — in the way we refine the inchoate notion of computability to arrive at the idea of effective computability (e.g. we abstract entirely away from consideration of the number of steps needed to execute an effective step-by-step computation, while insisting that we keep a low bound on the intelligence required to execute each particular step). Shapiro writes very well about this kind of exercise of reducing the amount of ‘open texture’ in an inchoate informal concept (or concept-cluster) and arriving at something more sharply bounded.

But another  question arises about the relation between the semi-technical notion of effective computability, once we’ve got there, and the notion of Turing computability. Now, Shapiro writes as if the move onwards from the semi-technical notion is (as it were) just more of the same. In other words, the same Lakatosian dynamic (rational conceptual development under the pressure of proof-development) is at work in first getting from the original inchoate notion of computability to the notion of effective computability, as in then going on eventually to refine out the notion of Turing computability. Well, that’s a good picture of what is going on at the conceptual level. But Shapiro seems to assume that this conceptual refinement goes along with a narrowing of extension  (in getting our concepts sharper, we are drawing tighter boundaries). But that doesn’t obviously follow.  An alternative picture is that once we have got as far as the notion of effective computable functions, we do have a notion which, though informal, is subject to sufficient constraints to ensure that it does indeed have a determinate extension (the class of Turing-computable functions). We can go on to say more about that extension, in coming up with various co-extensive technical notions of computability, but still the semi-technical notion of effective computability does enough for fix the class of functions we are talking about. For some exploration of the latter view, see for example Robert Black’s 2000 Philosophia Mathematica paper.

So a key issue here is this: is further refinement of “open texture” in the notion of effective computability required to determine a clear extension? Shapiro seems to think so. But looking at his paper, it is in fact difficult to discern any argument for supposing that things go his way. He is good and clear about how the notion of effective computability gets developed. But he seems to assume, rather than argue, that we need more of the same kind of conceptual development before we are entitled to settle the Turing computable/the recursive as a canonically privileged class of effectively computable function. But supposing that these are moves of the same kind is in fact exactly the point at issue in some recent debates. And that point, to my mind, isn’t sufficiently directly addressed by Shapiro in his last couple of pages to make his discussion of these matters entirely convincing.