Peter Smith's Blog, page 98

‘But pardon, and gentles all’

November was a busy month. A wonderful week out in Vienna (not to mention the time out before and after, getting ready and recovering from the excitements!). Peter Johnstone’s tough category theory lectures to keep on top of. Reading for the 2016 version of the Teach Yourself Logic guide to be done.

The Gentle Introduction to matters categorial has, therefore, not got anywhere near as much attention as I would have liked. Pardon, gentles all.

I have, however, uploaded a new version — now 171 pages, with two short new chapters (one either side of the chapter on exponentials). Prompted by Paolo Giarrusso, I’ve completely recast what was a short and potentially misleading section on subobjects into a standalone chapter. And I’ve added another chapter on some mathematical gadgets to be found inside categories, namely group objects and natural number objects (though as you’ll see the current version ducks out of giving a clean proof of the final stated theorem on recursion). I have also tinkered elsewhere with the first dozen chapters — the ones preceding the introduction of functors — at quite a few scattered points, not least in sorting some typos. The later chapters from functors onwards, by contrast, remain untouched.  As I say, not the state that I’d like the Gentle Introduction to have got to. But I won’t have much time to look at it again over the next few weeks (for various nice reasons), so I thought I should at least make available such improvements as I have been able to make. Here, then, is the latest version.

So please do continue to “piece out our imperfections with your thoughts” and let me know of corrections, obscurities, possible improvements etc.

And “your humble patience pray/Gently to hear, kindly to judge” these efforts so far!

Book Note: Tony Roy, Symbolic Logic, #1

Tony Roy (Philosophy, California State University, San Bernardino) has generously made available his Symbolic Logic: An Accessible Introduction to Serious Mathematical Logic. I’m commenting here on the version of October 6, 2015. The full main text is no less than 746 pages long, and is followed another 180 pages of worked answers to exercises. So this really is a major endeavour. But despite the great length, it doesn’t range widely: the discussion is “ruthlessly directed at core results” in the hope of thereby indeed making them as accessible as possible. That’s a good goal to have.

The text is divided into four parts. First, The Elements (introducing axiomatic and natural deduction presentations of FOL); second, a brief Transition part (including material on mathematical induction); third, Classical Metalogic, getting as far as touching on compactness and the L-S theorems; fourth, Logic and Arithmetic. I will comment about these four parts in four posts.

Roy isn’t very explicit about his intended audience: but reasonably high-flying mathematicians will, surely, find the 327(!) page Part I much too slow and laboured. Rather, this text goes at the sort of pace, and has the sort and level of coverage, that we expect in first ‘baby logic’ books aimed at non-mathematical philosophers who may have done a critical reasoning course, but otherwise are new to the subject. So what will such a student reader find: how will he or she cope?

The first chapter gives the usual sort of account of the informal notions of validity and soundness. This does the job, though we can quibble about details. For example, I don’t like to define an argument in such a way that almost no mathematical proof is an argument (Roy’s arguments have just premisses and a conclusion, with no room for intervening steps!). I’m not sure what is gained by defining validity in terms of there being no consistent story in which all the premisses are true and the conclusion false. What makes a story consistent other than its ingredient propositions being possibly true together? But if we have that notion of being possibly-true-together, then we can directly define validity in terms of that. Again, the brief section on validity and form needs to say more: students need to get the idea that a form of argument that is not generally valid can have valid instances.

Chapter 2 is on Formal Languages (or rather the syntax thereof). Roy discussed both sentential and quantificational languages here (but you could easily extract from this and following chapters the bits about sentential logic and read all those through before tackling  any quantificational logic). The official choice of languages is austere, with only 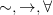as basic, with other connectives and the other quantifier introduced as abbreviations. Not my preference for an introductory book: for one thing, it is better to start with 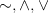and show how very nicely things go with these, before trying to sell the material conditional to sceptical philosophy students! For another thing, if philosophers are later to meet non-classical logics where the connectives/quantifiers aren’t inter definable, it’s better to keep things separate at the outset. But those considerations apart, this chapter is routine and clear enough.

Chapter 3 continues the syntactic theme and tackles Axiomatic Deduction. Roy himself notes that the reader might well want to skip this and return to it later. We get a standard Hilbert System (though unadorned with the Deduction Theorem at this stage, so unfriendly). As e.g. in Mendelson, we end up doing logic at one remove, with derivations all metalinguistic: which is fine if you make it transparently clear what is happening. But I don’t think Roy pulls this off. For example, he defines consequence (syntactic consequence in a deductive system) as holding between formal wffs. But then he slips unannounced into talking about consequence as a relation between sentence forms or schemata, and his examples of derivation become lists of schemata. 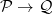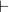A more minor thing, but he sloppily states the modus ponens rule  as ,   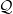— which on the standard understanding of is a proposition (or a schema for one) not the articulation of a rule. More seriously, the  presentation of the quantification rules and identity rules are, I think, likely to rather too quick for the intended neophyte audience. So overall, not a particularly successful chapter, I think.

Chapter 4 is on Semantics. Wffs of the formal languages are given valuations in the standard way. Though he calls valuations interpretations, Roy doesn’t actually seem to give the wffs of a formal sentential language, for example, any interpretative content — so philosophers might balk at the idea that we indeed have any object languages in play here.  Prescinding from general worries of that kind, however, I found the details of the treatment of quantificational semantics unhelpfully messy: there are a number of standard textbooks which do things in a more student-friendly way. I’m inclined to say much the same about the 70 page Chapter 5 which, perhaps rather late in the day,  is on Translation: to my mind, this often makes unnecessarily heavy weather of simple things. Students don’t need to bring to bear the official apparatus of quantificational semantics in order to work with translations to and from the formal languages.

Chapter 6 is 120 pp. on Natural Deduction, and presents a Fitch-style system, now with the usual four  connectives and both quantifiers. And Roy also introduces  into the system as a new symbol treated as an abbreviation for some contradiction: but this addition doesn’t seem to be handled tidily. The chapter, however, provides a great deal of help on proof-strategy for students using a Fitch-style system and could prove useful. Though a complaint might be that there isn’t a clean enough separation between (i) getting across a basic understanding of  the rules and of how the system works and (ii) the provision of heuristics for proof-discovery. And I suppose that a worry is that the mathematically ept won’t need anywhere near so much by way of heuristics, while the philosophers who primarily need to get to understand how proofs work (but needn’t fret so much about learning to roll their own proofs) could get lost in all the details.

Which all sounds a bit ungrateful! But, leaving price considerations aside, there is a lot of competition at this level from some very fine introductory logic books for the non-mathematical which are more polished and to my mind better organized. To be continued

Teach Yourself Logic 2016 — Last call for suggestions!

As I’ve noted, it is time to update the much-downloaded Teach Yourself Logic Study Guide for 2016, and I’ve recently made a start working through the current version.  So far, the editorial tinkering has been plentiful but minor as far as content is concerned, and even after quite a bit of thought I’m not finding myself inclined to make changes to the main recommendations in the early chapters. As for form, I’ve decided to keep the one-big-PDF format, rather than go over to a suite of webpages: but I hope the new version will be just a bit easier to find your way around (even such a simple thing as setting off main recommendations in text boxes makes the Guide look less daunting, more navigable).

So now I ask again: any suggestions for additions, improvements? In particular, are there any sets of freely available online lecture notes (your own or by others!) that are especially good and appropriate for self-study?

To repeat, suggestions from logicians at any stage of their career, whether taking first steps or on their zimmer frame, will be most welcome — either in the comments below, or by email (address at the bottom of my “about” page here).

A moment of cheer

For ever and a day, the old have bemoaned the state of the world and how it is now all going to the dogs. But it is difficult not to feel that, yes, even here in Europe, things really are going badly wrong. Certainly, I’ve found recent events more than usually unsettling and depressing. I offer then something to cheer us up for a moment.

In fact, Sabine Devieilhe’s whole Rameau disc ‘Le Grande Théâtre de l’Amour’ is terrific. Her stunning singing is matched by a very thoughtfully constructed programme: unlike some recital discs which can pall, the way that arias are interspersed with orchestral interludes means you can sit and listen straight through the whole disc with unalloyed delight. Recommended, then, if you too are feeling in need of something life-affirming.

Postcard from Vienna

Ephesos Museum, Vienna

A week in Vienna, staying in the Innere Stadt where The Daughter is living for three months. Some unreasonably good weather, warm enough to take coffee sitting outside. The city looking wonderful in the bright sun. And then in a different way, looking wonderful again as we walk delightedly through the centre almost every night after dinner (the pleasure of doing this is of course tinged with shame and indeed anger when we think of the horrible experience of late night English city centres). The cityscapes, street after street, palais after palais, are extraordinary (and yes, we rather liked the caryatids everywhere, despite the Secessionists’ scorn).

The museums and galleries have bowled us over, stunning collections quite beautifully displayed (I’m running out of superlatives here) — and though busy at the weekend, they are not overwhelmed with visitors in the way that the National Gallery and British Museum are. Even modest cafés are as they should be. A very generous son-in-law takes us to Restaurant Steirereck, which  is as good as they say, not to mention the restaurant at Hotel Sacher. Going to the ballet at the Staatsoper has been another delight — seemingly a much more mixed and more relaxed audience than the London equivalent.

It has all been far, far too short. To our surprise, our embarrassing lack of more than a few German phrases has been little hindrance (rather, we’d immediately be addressed in English in shops or cafés if we’d been heard chatting together), and we’ve felt very relaxed here. We must return for longer next year (the joys of retirement); maybe we can arrange a house swap …

Gently into November

I have just put an update for the Gentle Introduction to category theory online. Things have been moving pretty slowly (pressure of other interests, a planned chapter not really working out, spending far too much time revising earlier chapters, etc.); but we’ve inched forward to 157 fun-packed pages. Again, this version is stopping far short of a natural break point. But I’ll not be able to return to this for a few weeks, so I thought I should at least make available the best version of the earlier chapters I now have, and I can add three new chapters. (I note the newly added Theorem 63 which corrects a terrible blunder in some remarks in an earlier version! No promises that there aren’t more blunders to be found.)

 

Pausing en route

Clare Bridge, from Garret Hostel Bridge, October

One route from home to what passes for work takes me over Garret Hostel bridge; and early in the morning, before the tourists arrive and crowd the bridge, I can pause to take in the view which never ceases to delight.

These days, at the end of the lane, I go right, to where the mathematicians hang out at CMS, rather than left to old philosophical haunts. But I know very few of the philosophers now, and some mathmos have been kindly welcoming. Moreover, I find the café at CMS really rather conducive to work (if we can forget about the grimly bad coffee). So here I am at lunchtime, pausing for a while, as I try to batter the next few chapters of the Gentle Guide into shape, surrounding by the buzz of conversations and on-going supervisions at adjacent tables.

I have been going to Peter Johnstone’s Category Theory lectures three times a week. Rewarding, and something of an advertisement for old-school chalk-and-talk lectures — the chalk providing exemplary notes, the obiter dicta illuminating. But tough going. Seven lectures in, and we are already proving that a functor 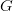 to 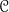has a left adjoint iff for every 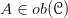the comma category has an initial object. Kudos to those students who fully are on the pace. But also, judging from a conversation or two, a supplementary discursive Gentle Introduction to help ease the path into category theory might yet be appreciated by some. Onward!

Teach Yourself Logic — suggestions? [Repost]

[I posted this back in August: and I’m moving this to the front of the blog to invite more contributions/suggestions!]

I haven’t looked at all at the Teach Yourself Logic Study Guide since the 2015 version came out on January 1st. I earlier had it in mind to do a mid-year update in time for the new (northern hemisphere) academic year: but that bird has long flown. The main Guide continues to be downloaded eighty or more times a month. It certainly seems to serve some need, and I get appreciative emails.  So I will put time aside over the coming months to get a 2016 version ready for next January 1st.

So now’s the time for feedback on both style and content. As far as style goes, while keeping to the spirit of the present Guide, what would make it more user-friendly? Should I keep the one-big-PDF format, or go over to a suite of webpages? [Added: after thinking a bit, I continue to incline strongly to the PDF format — it is easier to maintain, but also easier to read off line, and for students to work with by highlighting, commenting, etc. onscreen. But thoughts on style/layout etc. are still very welcome.]

As to content, any suggestions for additions, improvements? One thing I’ll want to say something about is The Open Logic project [added: I’ve posted some thoughts that  recently] But are there more conventional new(ish) publications, or overlooked older publications,  that could definitely rate a recommendation for student use?

Feedback from logicians at any stage of their career, whether taking first steps or on their zimmer frame, will be most welcome — either in the comments below, or by email (address at the bottom of my “about” page here).

And now for something completely different ….

And it is just Week 3 …

Moving gently on …

Autumn sun, Cambridge on the first day of lectures

I’m planning to go to a couple of lecture courses this term (including Peter Johnstone’s famed, take-no-prisoners, category theory course), and probably will join in a weekly reading group too. I also need to do quite a bit of other reading over the coming weeks if I’m to put together a decent update for the Teach Yourself Logic guide for 2016. Hence work on revising the category theory notes — already going at, shall we say, a rather gentle pace — will no doubt slow even more. So I thought I would put online the current version of Category Theory: A Gentle Introduction even though it doesn’t reach a natural break point. So far then, the now fourteen chapters (123 pp.), after introducing categories, consider limits and exponentials (constructions within categories) before moving on to start talking about functors (maps between categories). The category theory page here indicates which chapters to then read in the old notes, if you are feeling suitably enthused!