Peter Smith's Blog, page 97
December 23, 2015
A Christmas card

Gentile da Fabriano, Adoration of the Magi (detail), 1423
With all good wishes for a very happy and peaceful Christmas.
December 22, 2015
Serendipity
 We have far too many books for a house this small, despite our best efforts to make room on shelves by passing on the unloved or the never-to-be-reread to Oxfam. So these days, we try not to buy a newly published book if neither of us is going to read it more or less immediately (of course, a different rule applies to happy second-hand finds). That’s why, when Kate Atkinson’s companion piece to her truly brilliant Life after Life came out, despite our both very much looking forward to reading it, we didn’t buy it immediately, both already having tall piles of books waiting for us. And then it got to the point when a paperback was announced for the end of this month, and we decided to hang on and get it to read over festive season.
We have far too many books for a house this small, despite our best efforts to make room on shelves by passing on the unloved or the never-to-be-reread to Oxfam. So these days, we try not to buy a newly published book if neither of us is going to read it more or less immediately (of course, a different rule applies to happy second-hand finds). That’s why, when Kate Atkinson’s companion piece to her truly brilliant Life after Life came out, despite our both very much looking forward to reading it, we didn’t buy it immediately, both already having tall piles of books waiting for us. And then it got to the point when a paperback was announced for the end of this month, and we decided to hang on and get it to read over festive season.
But ah, a couple of weeks ago, in the National Trust shop at Wimpole, there it was — an almost pristine copy of A God in Ruins. The beautifully produced hardback for less than half the cost of a paperback. And it’s quite unreasonably cheering — isn’t it? — this kind of serendipitous find. Well ok, not that serendipitous, when you think about it: Kate Atkinson is a best-selling author, we often drop in to take a quick look at the book shelves of charity shops large and small, so I suppose it was pretty likely that we’d stumble on a copy over the months since it came out. But even that thought doesn’t make the find less cheering. It isn’t the matter of saving a few pounds (or of giving the money to a charity rather than a chain bookstore); that’s nice, to be sure, but it doesn’t account for the pleasure, the happy feeling engendered by the little smidgin of good fortune. And it’s the sort of little thing that sticks in the mind, “Do you remember finding that by chance when we were on holiday in …?”, it becomes part of your history of your encounter with the book in a way that just marching into Blackwells and picking the volume off a pile never does.
It is, or rather was, the same with CDs, the pleasure of the happy find in charity shops of something well-known that you’ve been wanting for a while, or of something quite obscure but intriguing. I had much more enjoyment over some years acquiring the complete Hyperion Schubert Edition — all 37 volumes of Graham Johnson’s astonishing exploration of all Schubert’s songs with various singers — mostly second-hand than I ever would have done just buying the lot new. I have had more fun again discovering baroque composers you’ve never heard of, or later obscure Bohemians, and the rest. (Of course there are plenty of misses as well as the hits, but the few pounds have gone to charity, so the misses don’t matter at all.) But now I mostly use Apple Music to stream music, for there is precious little space for more CDs; and I miss that kind of serendipity. Yes, of course, there is an unending source of music to explore there for the small subscription. Yes, of course, you make happy finds. But, dinosaur that I am, it just doesn’t feel the same.
No way, though, are we swapping real books for e-books. Putting a few on the iPads when travelling is fine: but a well-made real book remains a continuing delight that we are not giving up. So we’ll carry on the pleasurable truffling through the charity shops: it’s the splendid Oxfam bookshop in Saffron Walden tomorrow, I think …
And how was A God in Ruins? As good as they say. Just wonderful.
Teach Yourself Logic 2016
You need something good to read over the holidays; so here is the Teach Yourself Logic 2016: A Study Guide!
For anyone who doesn’t know TYL, it is aimed at philosophers (who have already done a baby logic course) and mathematicians who are trying to teach themselves some mathematical logic and need a guide through the very large literature.
For those who are familiar with the 2015 version, there are some presentational changes aimed at making the Guide look a bit less daunting and more manageable, a few new recommendations or changes of view, and a lot of minor tinkering.
As always, constructive comments are immensely welcome. And many thanks to those who have made suggestions over the last year. I fear I may have overlooked/forgotten about some good ones: in which case, nag me! But most logic teachers are busy people, and haven’t time to wade through an 89 page Guide, however zestfully written it is. So, in the new year, I might start putting some cut-down excerpts here on the blog, to ask for feedback on specific sections. I’m sure all kinds of improvements could be made; but having spent quite a bit of time on the new version already, and to prevent myself tinkering away more over the holidays when I should be doing more fun things, here it is. Enjoy!
December 16, 2015
Publicize your new book here?
It is difficult to know which statistics package to believe. Google Analytics says that Logic Matters steadily gets something in the order of 12,000 unique visitors a month, AWStats puts it around 18,000. And both say that the number of visits a month is at least three times as high. The WordPress stats are significantly higher again. It’s really nice to know that I’m not talking to myself!
The costs of hosting, backup, the domain names, etc. are not trivial. But they are only of the order of £200 a year, and since I do get a lot out of keeping Logic Matters going, that’s fine by me. So I’m not inclined to go to the bother of trying to emulate some Well-Known Blogs and seek paid advertising (I doubt that I’m missing out on much, given that the traffic on this site, though substantial, is not in the same league).
However … If you have a new book in mathematical logic or philosophy of maths/philosophy of logic that you would like to publicize at the top of the side bar that appears on most pages — i.e. where the cover image of my Gödel book currently appears –then get in touch (email at the foot of the “About” page). If I like the sound of it, then the deal will be that you send me a free copy of the book, and then you get at least four weeks in the sidebar (cover image linked to publisher’s site or Amazon). I save a bit on book bills, and you — for the cost of postage and one of your free author’s copies — get exposure to a large but very select audience of logic fans. Fair swap?
December 15, 2015
Conference: Philosophy of mathematics — truth, existence and explanation.
Philosophy of maths AND Italy — what’s not to like? So let me note that the second conference of the Italian Network for the Philosophy of Mathematics has been announced for 26-28 May 2016, University of Chieti-Pescara, Chieti, Italy.
The invited speakers are Volker Halbach (University of Oxford), Enrico Moriconi (University of Pisa), Achille Varzi (Columbia University) together with ‘early career’ speakers Marianna Antonutti Marfori (IHPST, Paris) and Luca Incurvati (University of Amsterdam).
This is an English language conference, and there is a call for abstracts for contributed talks “in any area of philosophy of mathematics connected with the issues of truth, existence, and explanation”. All the details can be found at the FilMat website here.
December 14, 2015
Book Note: Leary and Kristiansen, A Friendly Introduction …
I’ll return to say more about Tony Roy’s text in a day or two, but here is a new version of my earlier Book Note on the ‘Friendly Introduction to Mathematical Logic’, revised to take into account the expanded second edition. As you will see, very warmly recommended.
 Christopher C. Leary and Lars Kristiansen’s A Friendly Introduction to Mathematical Logic (Milne Library 2015: pp. 364 — ISBN 978-1-942341-07-9) is the second, significantly expanded, edition of a fine book originally just authored by Leary (Prentice Hall, 2000: pp. 218). The book is now available at a very attractive price; the main differences between the editions are a long new chapter on computability theory, and some 75 pages of solutions to exercises.
Christopher C. Leary and Lars Kristiansen’s A Friendly Introduction to Mathematical Logic (Milne Library 2015: pp. 364 — ISBN 978-1-942341-07-9) is the second, significantly expanded, edition of a fine book originally just authored by Leary (Prentice Hall, 2000: pp. 218). The book is now available at a very attractive price; the main differences between the editions are a long new chapter on computability theory, and some 75 pages of solutions to exercises.
So how friendly is A Friendly Introduction? – meaning, of course, ‘friendly’ by the standard of logic books!
I do like the tone a great deal (without being the least patronizing, it is indeed relaxed and inviting), and the level of exposition seems to me to be very well-judged for an introductory course. The book is officially aimed mostly at mathematics undergraduates without assuming any particular background knowledge. But as the Preface notes, it should also be accessible to logic-minded philosophers who are happy to work at following rather abstract arguments (and, I would add, who are also happy to skip over just a few inessential elementary mathematical illustrations).
What does the book cover? Basic first-order logic (up to the L-S theorems), the incompleteness theorems, and some computability theory. But by being so tightly focused, this book rarely seems to rush at what it does cover: the pace is pretty even. The authors do opt for a Hilbertian axiomatic system of logic, with fairly brisk explanations. (If you’d never seen before a serious formal system for first-order logic this could initially make for a somewhat dense read: if on the other hand you have been introduced to logic by trees or seen a natural deduction presentation, you would perhaps welcome a paragraph or two explaining the advantages for present purposes of the choice of an axiomatic approach here.) But the clarity is indeed exemplary.
Some details Ch. 1, ‘Structures and languages’, starts by talking of first-order languages (The authors make the good choice of not starting over again with propositional logic, but assume that most readers will know their truth-tables so just give quick revision). The chapter then moves on to explaining the idea of first order structures, and truth-in-a-structure. There is a good amount of motivational chat as we go through, and the exercises – as elsewhere in the book – seem particularly well-designed to aid understanding. (The solutions to exercises added to the new edition makes the book even more suitable for self-study.)
Ch. 2, ‘Deductions’, introduces an essentially Hilbertian logical system and proves its soundness: it also considers systems with additional non-logical axioms. The logical primitives are ‘ ∨ ’, ‘¬’, ‘∀’ and ‘ = ’. Logical axioms are just the identity axioms, an axiom-version of ∀-elimination (and its dual, ∃-introduction): the inference rules are ∀-introduction (and its dual) and a rule which allows us to infer φ from a finite set of premisses Γ if it is an instance of a tautological entailment. I don’t think this is the friendliest ever logical system (and no doubt for reasons of brevity, the authors don’t pause to consider alternative options); but it certainly is not horrible either. If you take it slowly, the exposition here should be quite manageable even for the not-very-mathematical.
Ch. 3, ‘Completeness and compactness’, gives a nice version of a Henkin-style completeness theorem for the described deductive system, then proves compactness and the upward and downward Löwenheim-Skolem theorems (the latter in the version ‘if L is a countable language and 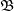 is an L-structure, then
is an L-structure, then 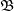 has a countable elementary substructure’ [the proof might be found just a bit tricky though]). So there is a little model theory here as well as the completeness proof: and you could well read this chapter without reading the previous ones if you are already reasonably up to speed on structures, languages, and deductive systems. And so, in a hundred pages, we wrap up what is indeed a pretty friendly introduction to FOL.
has a countable elementary substructure’ [the proof might be found just a bit tricky though]). So there is a little model theory here as well as the completeness proof: and you could well read this chapter without reading the previous ones if you are already reasonably up to speed on structures, languages, and deductive systems. And so, in a hundred pages, we wrap up what is indeed a pretty friendly introduction to FOL.
Ch. 4, ‘Incompleteness, from two points of view’ is a helpful bridge chapter, outlining the route ahead, and then defining 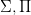 and
and 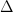 wffs (no subscripts in their usage, and exponentials are atomic — maybe a footnote would have been wise, to help students when they encounter other uses). Then in Ch. 5, ‘Syntactic Incompleteness—Groundwork’, the authors (re)introduce the theory they call N, a version of Robinson Arithmetic with exponentiation built in. They then show that (given a scheme of Gödel coding) that the usual numerical properties and relations involved in the arithmetization of syntax – such as, ultimately, Prf(m, n), i.e. m codes for an N-proof of the formula numbered n – can be represented in N. They do this by the direct method. That is to say, instead of [like my IGT] showing that those properties/relations are (primitive) recursive, and that N can represent all (primitive) recursive relations, they directly write down
wffs (no subscripts in their usage, and exponentials are atomic — maybe a footnote would have been wise, to help students when they encounter other uses). Then in Ch. 5, ‘Syntactic Incompleteness—Groundwork’, the authors (re)introduce the theory they call N, a version of Robinson Arithmetic with exponentiation built in. They then show that (given a scheme of Gödel coding) that the usual numerical properties and relations involved in the arithmetization of syntax – such as, ultimately, Prf(m, n), i.e. m codes for an N-proof of the formula numbered n – can be represented in N. They do this by the direct method. That is to say, instead of [like my IGT] showing that those properties/relations are (primitive) recursive, and that N can represent all (primitive) recursive relations, they directly write down 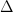 wffs which represent them. This is inevitably gets more than a bit messy: but they have a very good stab at motivating every step working up to showing that N can express Prf(m, n) by a
wffs which represent them. This is inevitably gets more than a bit messy: but they have a very good stab at motivating every step working up to showing that N can express Prf(m, n) by a 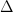 wff. If you want a full-dress demonstration of this result, then this is one of the most user-friendly available.
wff. If you want a full-dress demonstration of this result, then this is one of the most user-friendly available.
Ch. 6, ‘The Incompleteness Theorems’, is then pretty short: but all the groundwork has been done to enable the authors now to give a brisk but very clear presentation, at least after they have proved the Diagonalization Lemma. I did complain that, in the first edition, the proof of the Lemma was slightly too rabbit-out-of-a-hat for my liking. This edition I think notably softens the blow (one of many such small but significant improvements, as well as the major additions). And with the Lemma in place, the rest of the chapter goes very nicely and accessibly. We get the first incompleteness theorem in its semantic version, the undecidability of arithmetic, Tarksi’s theorem, the syntactic version of incompleteness and then Rosser’s improvement. Then there is nice section giving Boolos’s proof of incompleteness echoing the Berry paradox. Finally, the second theorem is proved by assuming (though not proving) the derivability conditions.
The newly added Ch. 7, ‘Computability theory’ starts with a very brief section on historical origins, mentioning Turing machines etc.: but we then settle to exploring the $\latex \mu$-recursive functions. We get some way, including the S-m-n theorem and a full-dress proof of Kleene’s Normal Form Theorem (with due apologies for the necessary hacking though details) and meet the standard definition of the set  where
where  is the domain of the computable function with index
is the domain of the computable function with index  . The uncomputability of
. The uncomputability of  is then used, in the usual sort of way, to prove the undecidability of the Entscheidungsproblem, to re-prove the incompleteness theorem, and in tackling Hilbert’s 10th problem. This is all nicely done in the same spirit and with the same level of accessibility as the previous chapters.
is then used, in the usual sort of way, to prove the undecidability of the Entscheidungsproblem, to re-prove the incompleteness theorem, and in tackling Hilbert’s 10th problem. This is all nicely done in the same spirit and with the same level of accessibility as the previous chapters.
Summary verdict If you have already briefly met a formally presented deductive system for first-order logic, and some account of its semantics, then you’ll find the opening two chapters of this book very manageable (if you haven’t they’ll be a bit more work). The treatment of completeness etc. in Ch. 3 would make for a nice stand-alone treatment even if you don’t read the first two chapters. Or you could just start the book by reading §2.8 (where N is first mentioned), and then read the excellent ensuing chapters on incompleteness and computability with a lot of profit. A Friendly Introduction is indeed in many ways a very unusually likeable introduction to the material it covers, and has a great deal to recommend it. Very warmly recommended (so ensure that your library gets a copy!)
December 13, 2015
Postcard from Florence

Bronzino meets the Ponte Vecchio
To Florence for the better part of six days. The city is as usual wonderful in December, far from the summer heat and the summer crowds of foreign tourists (though we forgot about the Immacolata Concezione holiday, so there are Italian crowds for a couple of days). Blue skies and bright sun too.
The Uffizi is at long last being renovated and pictures rehung (the parts so far done are a huge improvement): the Leonardo Annunciation particularly beautifully displayed — On a sunny winter’s day, the view from San Miniato is breathtaking — Buy soap in that most beautiful shop, the Officina Profumo-Farmaceutica di Santa Maria Novella, complete with its own frescos — The Magi Chapel in the Palazzo Medici Riccardi as stunning as ever, and almost empty, so we can stay as long as we want — Night time walks round Florence, with added light shows (as above) — Rigoletto, conducted by Zubin Mehta, wonderfully sung with a fine cast and only slightly daft staging, then walking back along the Arno late on a fine night — A fresco day (Santa Croce, the Brancacci Chapel, and not least Ghirlandaio at Santa Maria Novella) — Fiesole — and more …
We eat and drink very well too (notably at Olio e Convivium and Il Santo Bevitore). So we have an exceptionally good time. We know we are lucky to be able to do this kind of thing.
December 4, 2015
Book Note: Tony Roy, Symbolic Logic, #2
To continue, then, with the comments on Tony Roy’s Symbolic Logic: An Accessible Introduction to Serious Mathematical Logic, Part II is called “Transition: Reasoning about Logic”, and is almost another 100 pages, though it consists of just two chapters.
Chapter 7 is a curious affair. It’s called “Direct Semantic Reasoning”, and the aim is to get the student to be able to use their understanding of the official semantics to demonstrate that, e.g., (i) 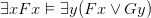 or more challengingly (ii)
or more challengingly (ii) 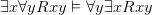 , while also being able to show e.g. (iii)
, while also being able to show e.g. (iii)  . And yes, we of course want students to be able to do these things. Or rather more carefully, we want a student to able to produce informal but rigorous proofs of entailments given the definition of semantic consequence, and to produce counterexamples to witness non-entailments. This amounts to learning how to do some bits of (pretty elementary) mathematical reasoning, and students coming from a non-maths background need to be given some exemplars and models of this sort of informal reasoning done with the right amount of detail to pass muster.
. And yes, we of course want students to be able to do these things. Or rather more carefully, we want a student to able to produce informal but rigorous proofs of entailments given the definition of semantic consequence, and to produce counterexamples to witness non-entailments. This amounts to learning how to do some bits of (pretty elementary) mathematical reasoning, and students coming from a non-maths background need to be given some exemplars and models of this sort of informal reasoning done with the right amount of detail to pass muster.
But Roy is keen to replace informal proofs with formal derivations set out in natural deduction style, and the results seem to me to be rebarbative and consequently unhelpful. It is difficult to believe that students will find their abilities at informal reasoning actually improved by the sort of messy regimentations we find in this chapter. Have a look at p. 364 and ask if this is likely to help a student who doesn’t immediately see why, morally, (ii) should be true.
In his Preface, Roy tries to make a case for his approach in this chapter, but I’m not convinced. And to the extent that the idea is to give students an example of working formally in reasoning about logic, then we have to hand a framework for formalizing semantic reasoning which is much, much more elegant — i.e. use semantic tableaux, which are designed for the job!
Chapter 8 is on Mathematical Induction. This starts with a general discussion of induction, with some simple arithmetical and geometrical examples. Roy then goes on to give some applications of induction to prove syntactic and semantic facts about his formal languages. The chapter seems pretty clear, though as before things are perhaps rather stretched out. However, philosophy students needing to get their heads round the idea of induction and struggling with brisker presentations could very well find this a useful compendium.
To be continued.
December 3, 2015
How about editing ANALYSIS?
The philosophy journal Analysis has only had three editors in the last forty years (a rather remarkable record, I suppose). Christopher Kirwan edited it from late 1976 to 1987; I was editor from 1988 to 1999; and Michael Clark has been editor ever since 2000.
But Michael has now announced he wishes to relinquish the editorship next year. I hope his successor will be as devoted to that so-time-consuming job as he has been.
It is surely good for philosophy to have a range of different journals with their own quirks and individual flavours; and so it is surely good for philosophy too if there is someone (or maybe some small team) willing to take charge of an editor-run journal like Analysis. Yet — unless things have radically changed just recently — editing a journal counts for very little in the metrics by which either individuals or their departments are judged. And other pressures on people’s time of course get only worse. So good luck to the Analysis Committee in finding someone else to take on the editorship.
I guess I’m glad I did the job (though I carried on a couple of years too long). That earlier timeslice of myself enjoyed it — though I wouldn’t see the attraction now, since I’ve so lost the taste for most philosophy. But maybe that change of heart isn’t as radical as it sounds. What made me quite a good editor (which people said I was) can’t be disconnected from fact that even then I thought that a lot of philosophy is very dull indeed, and of the potentially interesting stuff, lots is just not very good. Being very hard to please made it rather easier, perhaps, to crack on with the business of selecting out what eventually got published. And when I did get enthused, I was correspondingly willing to put in (when needed) a lot of editorial effort to help improve the paper.
It all seems a long time ago. But for anyone who might think about picking up the torch, the headline from the official notice is that interested parties (expected to be from the UK) should contact Dr Ben Colburn, at analysistrust.secretary@oup.com (soon).
December 2, 2015
‘But pardon, and gentles all …’
November was a busy month. A wonderful week out in Vienna (not to mention the time out before and after, getting ready and recovering from the excitements!). Peter Johnstone’s tough category theory lectures to keep on top of. Reading for the 2016 version of the Teach Yourself Logic guide to be done.
The Gentle Introduction to matters categorial has, therefore, not had anywhere near as much attention as I would have liked. Pardon, gentles all.
I have, however, uploaded a new version — now 171 pages, with two short new chapters (one either side of the chapter on exponentials). Prompted by Paolo Giarrusso, I’ve completely recast what was a short and potentially misleading section on subobjects into a standalone chapter. And I’ve added another chapter on some mathematical gadgets to be found inside categories, namely group objects and natural number objects (though as you’ll see the current version stops short of giving a clean proof of the final stated theorem on recursion). I have also tinkered elsewhere with the first dozen chapters — the ones preceding the introduction of functors — at quite a few scattered points, not least in sorting some typos. The later chapters from functors onwards, by contrast, remain untouched. As I say, not the state that I’d like the Gentle Introduction to have got to. But I won’t have much time to look at it again over the next few weeks (for various nice reasons), so I thought I should at least make available such improvements/corrections/additions as I have been able to make. Here, then, is the latest version.
So please do continue to “piece out our imperfections with your thoughts” and let me know of corrections, obscurities, possible improvements etc. And I “your humble patience pray/Gently to hear, kindly to judge” these efforts so far!



