Is 5x3 the same as 3x5?

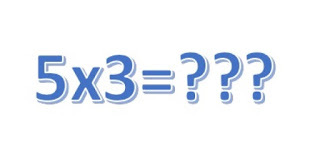The Internet has gone mildly bonkers over a child in America who was marked down in a test because when asked to work out 5x3 by repeated addition he/she used 5+5+5 instead of 3+3+3+3+3.

Those who support the teacher say that 5x3 means 'five lots of 3' where the complainants say that 'times' is commutative (reversible) so the distinction is meaningless as 5x3 and 3x5 are indistinguishable.
It's certainly true that not all mathematical operations are commutative. I think we are all comfortable that 5-3 is not the same as 3-5. 
However. This not true of multiplication (of numbers). And so if there is to be any distinction, it has to be in the use of English to interpret the 'x' sign.

Unfortunately, even here there is no logical way of coming up with a definitive answer. I suspect most primary school teachers would expands 'times' as 'lots of' as mentioned above. So we get 5 x 3 as '5 lots of 3'. Unfortunately that only works because they are using childish language. A secondary school teacher is more like to expand 'times' as 'multiplied by'. And so we get '5 multiplied by 3' - if you think about it, this clearly means 'take 5 and reproduce it three times.' So it means 5x5x5.

I think an excellent last word can be given to a Dr Petersen on the Math [sic] Forum: [Multiplication] is a commutative operation that can be modeled in two symmetrical ways as repeated addition (when applied to whole numbers).

Conclusion? The child was as correct to use this formulation as the one being taught, and the teacher was wrong to mark him/her down.