The Kepler Problem (Part 6)

In Part 4 we saw that the classical Kepler problem—the problem of a single classical particle in an inverse square force—has symmetry under the group of rotations of 4-dimensional space 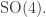Since the Lie algebra of this group is

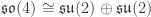
we must have conserved quantities

and

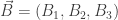
corresponding to these two copies of 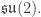The physical meaning of these quantities is a bit obscure until we form linear combinations

Then is the angular momentum of the particle, while 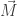is a subtler conserved quantity: it’s the ecc...