பொற்சுழல்

அன்புள்ள ஜெயமோகன் அவர்களுக்கு,

வணக்கம்

இரண்டாவது தாவரவியல் அறிமுக வகுப்பும் சிறப்பாக நடைபெற்றது. கோடை விடுமுறைக் காலமாகையால் நிறைய சிறுவர் சிறுமியர் கலந்து கொண்டிருந்தார்கள்.

இப்போது நிலவும் botanical illiteracy அடுத்த தலைமுறையிலும் தொடருமோ என நான் எப்போதும் கவலைப்படுவேன். எனவே கலந்துகொண்ட குழந்தைகளுக்குப் பிரத்யேகமான வகுப்பை நடத்தினேன், குறிப்பாகத் தாவரங்களின் கணித கணக்கீடுகள்குறித்து.

எனக்குத் தாவரங்கள்மீதான பிரமிப்புக்கும், பிரியத்துக்கும், மரியாதைக்கும் பல காரணங்கள் இருந்தாலும் அவற்றின் கணித அறிவு  அவற்றில் மிக முதன்மையானது. பூஜ்ஜியத்தை கண்டுபிடித்தோம் கணக்கைக் கண்டுபிடித்தோம், கணிதமேதைகள் நாங்கள் என்றெல்லாம் சொல்லிக் கொண்டிருக்கும் நமக்கு 700 மில்லியன்  வருடங்களுக்கு முன்பு தோன்றிய , ஒரே இடத்தில் வேர்கொண்டு நின்றிருப்பதால் நம்மைப் போலச் சிந்திக்கத் தெரியாது எனவே  மனிதர்களைவிடக் கீழான உயிரினங்கள் என்று நாம் நம்பும்   தாவரங்களின் துல்லியமான கணிதக்கணக்கீடுகள் மிகவும் ஆச்சரியம் அளிப்பவை.

நம்மில் இன்னும் அலாரம் வைத்துக் காலையில் எழுந்திருப்பவர்கள் இருக்கையில் 12 வருட காலக்கணக்கை துல்லியமாக நினைவில் வைத்து பெருங்கூட்டமாகக் காடுகளிலும், மலைச்சரிவுகளிலும் மலரும் குறிஞ்சி, 50/60 வருடங்கள் கழித்து உலகெங்கிலும் சொல்லி வைத்தது போல ஒரே சமயத்தில் பெருமலர்வை அளிக்கும் மூங்கில், வருடா வருடம் தவறாமல் குறித்த காலத்தில் மலர்ந்து கனியளிக்கும் மரங்கள் போன்ற காலக்கணக்கீடுகள் மட்டுமல்ல கணிதமும் அறிந்தவை.

மிகச் சாதாரணமாக நம் காலடியில் மிதிபடும் ஒரு சிறு செடியை எடுத்துக்கொண்டால் அதன் தண்டில் கணுவிடை வெளிகளின் துல்லியமான நீளம், மலர்களின் சமச்சீர் அமைப்பு,  இதழ்களின்  நீள அகலங்கள், சமச்சீரான கனிகளும் மஞ்சரிகளும், ஒரே நீளத்தில் அமைந்திருக்கும் மகரந்தத்தாள்கள்,  மிகச்சரியான அளவிலும் எடையிலும் இருக்கும் விதைகள் என அவற்றின் நுட்பமான கணக்கீடுகளை சொல்லிக் கொண்டே போகலாம். அவை அனைத்தும் இந்த மண்ணிலிருந்து, மண்ணுக்கடியிலிருந்து வெளிவந்த ஒரு உயிரினத்தின் அறிவினால் உருவானவை என்னும் பிரமிப்பு எனக்கு எப்போதும் இருக்கிறது.

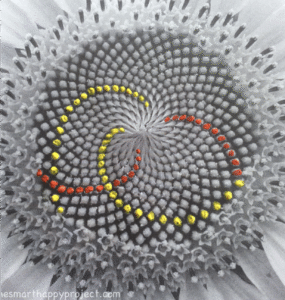
தாவரவியல் அறிமுக வகுப்பில் சூரியகாந்திப் பூக்களின் golden angle என்னும் மிகச்சரியான, துல்லியமான கணக்கீட்டில் விதைகள் அமைந்திருக்கும் புகைப்படங்களைச் சிறுவர்களுக்குக்  காட்டி விளக்கினேன்.

உண்மையில் அது மிக மிக ஆச்சரியமான நம்ப முடியாத தொன்று. எல்லாவற்றிலும் உயர்ந்தவர்களாகச் சொல்லிக்கொள்ளும் நம்மில் பலருக்கும் கணிதம் கடினமான பாடம். மாதா மாதம் பால் கணக்கைக்கூட பத்துத்தரம் போடுபவர்கள் இருக்கிறார்கள். கல்லூரிப் பாடங்களில் கணிதத்தை தேர்வு செய்யாமல் கணிதம் இல்லாத பிரிவுகளைக் கவனமாகத் தேர்வுசெய்து படிப்போர் பலலட்சம் பேர் இருக்கிறார்கள்

ஆனால் சூரியகாந்தி மலர்களின் (உண்மையில் அவை மலர்களல்ல மலர்த்தலைகள்) நடுவில் தட்டுப்போல அமைந்திருக்கும், விதைகள் உருவாகும் பகுதியில் இருக்கும் ஃபிபொனாச்சி கணித அடிப்படையிலான அமைப்பைக் கவனித்துப் புரிந்துகொண்டவர்கள் ஒருபோதும் தாவரங்கள் மனிதர்களைக் காட்டிலும் கீழ்நிலை உயிரினங்கள் என்று சொல்லவும் நினைக்கவும் மாட்டார்கள்.

12-ம் நூற்றாண்டைச் சேர்ந்த இத்தாலிய கணிதவியலாளர் லியனார்டோ.  அவரது தந்தைக்கு ’’நல்லியல்புகொண்ட’’ என்னும் பொருளில் பொனாச்சி என்னும் பட்டப்பெயர் இருந்தது. தந்தை இறந்த பின்னர் லியனார்டோவுக்கு ’பொனாச்சியின்  மகன்’ என்னும் பொருளில் ஃபிபொனாச்சி என்னும் புனை பெயர் அமைந்தது.  இந்து-அரபிக் எண்முறையை ஐரோப்பாவில் அறிமுகப் படுத்திய பிபொனாச்சி 13-ம் நூற்றாண்டில் வெளியிட்ட எண் கணித நூலான Liber Abaci யில் குறிப்பிட்டிருந்த  இந்தத் தொடரும் எண் வரிசை (அதை அவர் கண்டுபிடிக்கவில்லை என்றாலும்) அவர் பெயராலேயே பிபொனச்சி எண் வரிசையென அழைக்கப்பட்டது.

கணிதத்தில், ஃபிபொனாச்சி எண் தொடரில் உள்ள எண்களின் பட்டியல் 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ……..,∞ என்ற வரிசையில் குறிப்பிடப்படுகிறது. ஒவ்வொரு ஃபிபொனச்சி எண்ணும் முந்தைய இரண்டு எண்களைக் கூட்டுவதன் மூலம் பெறப்படுகிறது. பிபொனாச்சி நாள் கொண்டாடப்படும் நவம்பர் 23-ம் தேதியும் அதே எண் தொடர் வரிசையின் முதல் நான்கு எண்களில் தான் அமைந்திருக்கிறது  11/23 (November 23).

சூரியகாந்தி மலரின் நடுவில் அமைந்திருக்கும்   தட்டுப் போன்ற அமைப்பில் விதைகள் இந்த ஃபிபொனாச்சி எண்தொடரில் மிகச்சரியாக அமைந்திருக்கிறது

சூரியகாந்தியில் ஒவ்வொரு விதையும் ஒன்றுடன் ஒன்று உரசிக்கொள்ளாமல் ஒவ்வொரு விதையும் சரியாக வளர்வதற்கு இடம் அமைந்து , அனைத்து விதைகளுக்கும் சூரிய ஒளி சீராகக் கிடைக்கும் படி தங்கக்கோணம் (golden angle) என்று கணித்தத்தில் குறிப்பிடப்படும்  137.5° கோணத்தில் அமைந்திருக்கும் இரு பொற்சுழல்களும் (Golden spirals) உள்ளன.

சூரியகாந்தியின் மையத்தில் விதைகளால் ஆன எதிரெதிர் திசைகளில் வளைந்த இந்த இரண்டு தொடர்ச் சுழல்களும் ஒன்றை ஒன்று தழுவிக்கொண்டும் இடையிட்டும் மிக அழகாக ஒவ்வொரு விதைக்குமான இடத்தை உறுதி செய்து அமைந்திருக்கின்றன.

மலரின் மையத்தட்டில் வலதுபுறமாக  21  சுழல்பிரிகளும் இடதுபுறமாக 34 சுழல்பிரிகளுமாக மொத்தம் 55 சுழல்கள் இரு வெவ்வேறு திசைகளில் அமைந்திருக்கின்றன.

(சிறிய சூரியகாந்தி மலர்களில் இது 8 மற்றும் 13 என அமைந்திருக்கும்.)

இந்த நுட்பமான கணித அடிப்படையிலான அமைப்பு, இனப்பெருக்கம்  100 சதவீதம் நடைபெறுவதற்கும், ஒவ்வொரு விதைக்கும் சூரிய ஒளி சீராகக்கிடப்பதற்கும்,  மலருக்கு க்காற்றின் அழுத்தத்தைத் தாங்கும் வலிமை அளிப்பதற்குமாக அமைந்திருக்கிறது

இப்படியான சுழலமைப்புக்கள் இலைகளை, செதில்களை  விதைகளை மைய அச்சில் அல்லது தண்டின் மீது சுழற்சி அமைப்பில் பொருத்துவது தாவரவியலில் parastichies என்னும் பொதுவான பெயரிட்டு குறிப்பிடப்படுகிறது.

நுட்பமான எண்கணிதக் கணக்கீடொன்றை ஒரு அழகிய மலரில் காண்பது பெரும் வியப்பளிப்பது. இன்னும் ஏராளமான உதாரணங்கள் தாவரங்களின் கணித அறிவுக்கு இருக்கிறது.

இந்தப் பொற்சுழல் அமைப்பு தாழை மடல்களில், பைன் கோன்களில், அன்னாசியின் செதிலமைப்பில், கள்ளியின் முட்களில், DNA இரட்டைச்சுழல் அமைப்பில் என்று ஏராளமாக இயற்கையில்  அமைந்திருக்கிறது.

முதன்முதலாக ஊட்டி மார்க்கெட்டில் ரொமெனெஸ்கோ பூக்கோஸை பார்த்தபோது அப்படித்தான் உண்மையிலேயே திகைத்து விட்டேன். அத்தனை துல்லியமான கணிதக்கணக்கீட்டில் அமைந்திருக்கும் குட்டிக்குட்டி பூத்தலைகளை எப்படி பிய்த்துச் சமைத்து சாப்பிடுவதென்றே தெரியவில்லை.

கடந்த வாரம் பெங்களூருவிலும் அதே ரொமெனெஸ்கோ பூக்கோசை ஒரு பெரிய மாலில் பார்த்தேன்.கணிதத்தின்  பின்னப்பரிமாண அமைப்பில் ஒவ்வொரு பூக்கோசின் தலையும் ஃபிபொனாச்சி எண் வரிசைத்தொடரில் அத்தனை அற்புதமாக அமைந்திருக்கிறது.

வெண்டைக்காய் சாப்பிட்டால் கணக்கு நன்றாக வரும் என்று சொல்வதெல்லாம் எந்த அறிவியல் அடிப்படையும் இல்லாத ‘’கிளப்பி விடுதல்’’ வகை தகவல்தான். ஆனால் எனக்கென்னவோ இந்த ரொமெனெஸ்கோ பூக்கோசை சாப்பிட்டால் கணக்கு வரலாமெனத் தோன்றும். அத்தனை கணக்காக அது அமைந்திருக்கிறது.

பகலில் ஒளிச்சேர்க்கை மூலம் உணவைத் தயாரிக்கும் தாவரங்கள் இரவில் சேமிப்பில் இருக்கும் மாவுச்சத்தை அளந்து, விடியும் வரை தேவைப்படும் இடங்களுக்கு அவற்றைப் பங்கு போட்டு விநியோகிப்பது கண்டறியப்பட்டிருக்கிறது. வலசை போகும் பறவைகள் இப்படி உடலின் கொழுப்பளவை கணக்கிடுகின்றன

ஆப்பிளைப் போலச் சமச்சீரான கனிகள், கோடிக்கணக்கில் சிற்றிலைகளைக் கொண்டிருக்கும் ஒற்றை மரத்தில் மி மீ அளவில் இருக்கும் இலைக்காம்புகள் அத்தனையும் ஒரே அளவில் இருப்பது

மகரந்த சேர்க்கை செய்ய வரும் பூச்சிகள் அமர்ந்து மலரமுதை உண்ண வசதியான, அவை அமர்ந்தால் மலரமுதை உண்ணுகையில் மகரந்தம் அவற்றில் உடலில் படும்படியாகக் கணக்கிட்டு அளந்து வைத்த இடம் அளிப்பது

இலைக்காம்புகளின் நீளத்தைக் கூட்டியும் குறைத்தும் ஒரு அழகிய மலர்க்கொத்து போலச் செடியின் நுனியில் மட்டும் இலைகள் இருக்கும்படி அமைத்ச்து சூரிய ஒளியை வாங்கிக்கொள்ளும் குப்பை மேனிச்செடி.

பப்பாளிமரத்தின் கணித அடிப்படியில் அமைந்திருக்கும் இலைகளின் சுருளமைப்பு,

மக்காச்சோளக்கதிரில் விதைமணிகள் அமைந்திருக்கும் வரிசைச்சுழலும், வரிசைகளில் மணிகள் அமைந்திருக்கும்  கணக்கும்,

பெரணிகளின் இலைகளின் அடிப்புறம் இருக்கும் வித்துக்கள் அமைந்திருக்கும் வரிசையும் அப்படித்தான் மிகச்சீரான இடைவெளியில் செய்துவைத்தது போலவே அமைந்திருக்கும்.

அது போலவேதான் மரங்களின் கிளையமைப்பும். Branching architecture என்பது  மரங்களில் மிக அற்புதமான ஒரு அமைப்பு. winter habit இதை என்று  சொல்லப்படும் இலையுதிர்காலங்களில் மிகத்தெளிவாகக் காணலாம். எல்லா கிளைகளும் இலைகளுக்குச் சூரிய ஒளி கிடைக்கும்படி, ஒன்றுடன் ஒன்று குறுக்கிடாமல் மிக அழகிய அடுக்கிலும் சுழலிலும் அமைந்திருக்கும். இந்தக் கணித வடிவத்துக்கேற்றபடி கிளைகளின் தடிமன் கூடத் துல்லியமாகக் கணக்கிடப்பட்டிருக்கும்

அடிப்படை கணித விதிகளுக்குட்பட்ட  இப்படியான கிளைவளர்ச்சியும் விரிதலும் (branching fractals) தாவரங்களின் புத்திசாலித்தனதுக்கு மிக வெளிப்படையான ஒரு உதாரணமாக இருக்கிறது.

இந்தக் கணித வடிவங்களும் அமைப்புக்களும்  சவால்களை எதிர்கொண்டு அவற்றின் வாழ்தலை உறுதிப்படுத்தவும், இனப்பெருக்கம், ஒளிச்சேர்க்கை ஆகியவை சரியாக நடக்கவும் பல லட்சம் வருடங்களாக மெல்ல மெல்ல பரிணாம வளர்ச்சியில் உருவாகி வந்திருப்பவை.

தாவரங்களின் கணித அறிவை அறிந்து கொள்ளும்போது அவற்றின் மீதான மதிப்பும் அன்பும் மேலும் மேலும் அதிகமாகிறது.

தாவரங்களின் தண்டில் கணுவிடைவெளிகளின் நீளம், இலைக்காம்பின் நீளம், மலரிதழ்களின் ஒத்த அளவும் எண்ணிக்கையும் இவற்றைக் கணக்கிட்டு தாவரங்களின் கணித அறிவை கற்றுக்கொடுக்க என மிக எளிமையாக  சிறார்களுக்கான் ஒரு நாள் பயிலரங்கம் ஒன்றை நடத்தலாமென்றிருக்கிறேன். இதைக்குறித்து தமிழில் ஒரு நூலும் எழுதலாமென்றிருக்கிறேன்.

சிறார்களுக்கு  தாவரங்கள் குறித்த மிக முக்கியமானவற்றை கற்றுக் கொடுப்பதில் எனக்கும் பெரும் மனநிறைவு.  அவர்களுடன் நானும் புதிது புதிதாக கற்றுக்கொண்டே இருக்கிறேன். இந்த வாய்ப்புக்கென உங்களுக்கு எனது தனிப்பட்ட நன்றிகள்.

அன்புடன்

லோகமாதேவி

அன்புள்ள லோகமாதேவி,

பல ஆண்டுகளாக என் கையருகே இருந்துகொண்டிருக்கும் நூல்  Douglas Hofstadter எழுதிய Gödel, Escher, Bach. எனக்கு இது படித்துத் தீராத புத்தகம், நாய்பெற்ற தெங்கம்பழம் என்றும் ஒருவகையில் சொல்லலாம். முழுக்க புரியவுமில்லை, விடவும் மனமில்லை.

இது கணிதத்தின் அழகியலைப் பற்றியது. ஓவியம், இசை கணிதம் ஆகிய மூன்றும் சந்திக்கும் புள்ளி பற்றிய ஓர் ஆய்வு. உயர்நிலைக் கவிதைக்கு இணையாகச் சென்றுகொண்டிருக்கும் ஒரு நூல். அவ்வப்போது எடுத்து ஓரிரு பக்கங்களை வாசித்து ஓர் அழகியல் எழுச்சியை அடைவது என் வழக்கம். பிதகரஸ், யூக்லிட், மைக்கலாஞ்சலோ, கதே, பிகாஸோ என அனைவருமே ஓரிடத்தில் குவியும் நூல்.

ஈஷர்

எனக்கு அதில் பெருவியப்பு அளிப்பவர் ஈஷர்(M. C. Escher) விந்தையான அவருடைய காட்சியுலகம் என்னை கனவுகளில் எல்லாம் துரத்திக்கொண்டிருப்பது. அது ஜியோமிதி விந்தைகளாலானது. ஆனால் இயற்கையின் பேரழகை வெளிப்படுத்துவது. கலை எப்படி கணிதமாகிறது, கணிதம் எப்படிக் கலையாகிறது என்பதை வெளிப்படுத்தும் மகத்தான ஓவியங்கள் என்று அவற்றைச் சொல்லமுடியும். நவீன கணிப்பொறி வரைகலை உருவானபின் ஈஷரின் கற்பனைகளை மிகமிக முன்னெடுத்துச் சென்றுவிட்டார்கள். ஆனால் தொடக்கம் அவர்தான்.

(ஈஷரின் ஓவியங்களை அறிந்தவர்கள் Inception போன்ற படங்களை முற்றிலும் வேறொரு முழுமைக் கோணத்தில் ரசிக்க முடியும். அந்தப் படம் வந்தபோது நான் மீண்டும் ஈஷரின் உலகுக்குள் அலைந்தேன். ஆனால் தமிழில் எழுதப்பட்ட எந்த திரைவிமர்சனத்திலும் ஈஷர் பற்றி குறிப்பு இல்லை. எல்லாமே கதைச்சுருக்கம் மற்றும் கருத்து மட்டுமே, வழக்கம்போல)

ஈஷரின் ஓவியங்களுக்கு ஸ்வரங்களின் ஆடலில் உள்ள கணக்குகள் வழியாக பாக் கொண்டுள்ள ஒருமையை இந்நூல் விளக்குகிறது, எனக்கு புரியவில்லை. அஜிதனுக்குப் பிடிகிடைக்கலாம். ஆனால் அந்த ஓவியங்களைப் பார்த்தபின் பாக் இசையை கேட்டால் அவை மிகச்சரியாக நினைவில் வந்து இணைந்துகொள்கின்றன. என் கற்பனையில் ஈஷர் ஓவியத்தில் ஒரு போர்ஹெ. போர்ஹெதான் இலக்கியத்தில் சுழற்பாதைகளுக்கு இவ்வளவு பெரிய இடத்தை அளித்தவர்.

இயற்கையின் பொற்சுழல்களை உங்கள் கட்டுரை வழியாகப் பார்த்துக் கொண்டிருக்கிறேன். இவையனைத்தும் சீர்மை (symmetry) என்ற இயற்கையின் மகத்தான நெறியை நாம் கண்ணால் காணும் அனுபவங்களே என்று படுகிறது.

ஜெ