Carnap and the Diagonalization Lemma (Continued)
Let's distinguish what I'll call the Diagonalization Equivalence from the familiar Diagonalization Lemma. The former is a semantic claim: in the right conditions, for any one-place predicate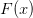 
of theory T there is a corresponding sentence 
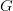such that 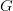is true if and only if 
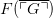is true. The latter is a syntactic claim: in the right conditions, for any one-place predicate 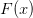of theory T there is a corresponding sentence 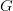such that 
.
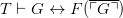In the previous post, I claimed that in his §35 Carnap proves the semantic Diagonalization Equivalence, which he uses in §36 to prove the semantic version of Gödel's First Theorem. But I said he doesn't prove the Lemma there or give the now canonical syntactic version of the Theorem (the one depending on the syntactic assumption of 
-consistency).
Well, no one has protested yet. So, thus emboldened, let me now stick my neck out further!
What happens later in the book? Carnap's notation and terminology together don't make for an easy read. But as far as I can see, when he returns to Gödelian matters later, he still is using the semantic Diagonalization Equivalence and not the syntactic Diagonalization Lemma. If the latter was going to appear anywhere, you'd expect to find it in §60 when Carnap returns to the incompleteness of arithmetics: but it isn't there. (An indication: Carnap here talks of provability being 'definable' in arithmetics, and it is indeed expressible — but we know it isn't capturable/representable by a trivial argument from the Diagonalization Lemma proper. So Carnap hereabouts is still dealing with semantic expressibility, and doesn't seem to invoke the syntactic notion of capturing/representing needed for the Lemma.)
So, in summary: Yes, Carnap gives a nice tweak to the argument in §1 of Gödel 1931 for the semantic incompleteness theorem, by generalizing the basic idea to give the Diagonalization Equivalence. But this isn't the modern Diagonalization Lemma. Which isn't to say that we can't get the Lemma easily using the wff Carnap constructs: however, as far as I can see, Carnap didn't explicitly take the step in 1934, even though he is often credited with it.
What am I missing?
