Carnap and the Diagonalization Lemma
Let me boldly fly a kite: this may be quite wrong, but do help me out if so! Anyway …
Carnap is often credited with proving the Diagonalization Lemma in Logische Syntax der Sprache. But, I claim, this is actually false if we understand 'Diagonalization Lemma' in what I take to be the usual modern sense. Why so?
Well, in §35 Carnap notes the general recipe for taking a one-place predicate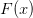 
and constructing a sentence 
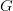such that 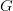is true if and only if 
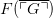is true, where as usual 
is the formal numeral for the Gödel number for .
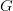Fine. But that claim about constructing a semantic equivalence isn't the Diagonalization Lemma as normally understood, which is a syntactic thesis, not about truth-value equivalence but about provability. It is the claim that, in the setting of the right kind of theory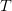 
, then for any one-place predicate 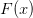we can construct a sentence 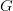such that 
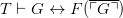. And Carnap doesn't prove that.
When we turn to §36, where Carnap proves the incompleteness of his system II, again he appeals to his semantic result not the syntactic Diagonalization Lemma. We now take the relevant predicate to be NOT-PROVABLE: so we get a sentence 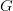which is true if and only if it isn't provable. And then Carnap appeals to the soundness of his system II to argue in the elementary way that 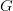isn't provable. So his is a version of the semantic incompleteness argument sketched in the opening section of Gödel 1931 (the one that appeals to a soundness assumption), and not a version of Gödel's official syntactic incompleteness argument which appeals to 
-consistency. Indeed, Carnap doesn't even mention -consistency in the §36 incompleteness proof. He doesn't need to.
Carnap doesn't use the theorem that his system II proves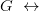 
NOT-PROVABLE
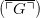, i.e. he doesn't appeal to an application of the Diagonalization Lemma in the modern sense. He doesn't need it, and he doesn't prove it.
So it is at best misleading to credit Carnap with the Lemma (unless that is qualified with a clear explanation that what is meant is a semantic result, not the syntactic one people usually mean).
If that's off-beam, do explain why!
