Greg Ross's Blog, page 4

Square Deal

From Catriona Agg’s endlessly rewarding Twitter feed:

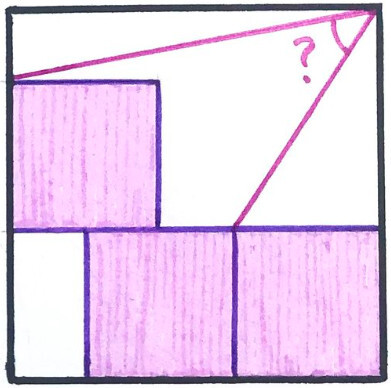
The three smaller squares are the same size. What’s the angle? (The outermost shape too is a square.)

At first it seems we have too little information, but it turns out the angle is invariant with the size of the larger square — grab point H and drag it left and right:

(GeoGebra resource by John Golden.)

Two Meetings

On Aug. 6, 1945, 24-year-old Jacob Beser was the radar specialist aboard the Enola Gay when it dropped the atomic bomb on Hiroshima.

Three days later, Beser was aboard the B-29 Bockscar when it dropped the bomb on Nagasaki.

He is the only person who served as a strike crew member on both missions.

Below him, Japanese marine engineer Tsutomu Yamaguchi endured the first bombing during a business trip to Hiroshima, then returned home to Nagasaki in time to receive the second.

He is the only person acknowledged by the Japanese government to have survived both bombings.

Up and Down

A remarkably simple question by Russian scientist A. Savin, from the September/October 1995 issue of Quantum:

A ping-pong ball is tossed into the air. Will it take longer to go up or to come back down?

The ball is always working against air resistance, so it’s losing energy all the time; at a given height, its total energy while rising is greater than while falling. The ball’s potential energy at this height is the same in both cases, so its kinetic energy (and hence its speed) is greater when it’s rising. So it takes longer to fall than to rise.

Black and White

By Sigurd Clausén. White to mate in three moves.

1. Kf5! Now the bishop must move, and then 2. h8=Q+ Bb8 3. Qh1#

Note that the king’s waiting move must be to f5. Moving to a black square leaves him vulnerable to a check; moving to the h-file blocks the queen’s access to h1; and moving to f3 blocks the queen’s final checkmate.

If 1. Kf5 Be5 then 2. h8=Q+ Bxh8 3. f8=Q#.

From Eskilstuna-Kuriren, 1931.

Never Mind

In 1812, inventor Charles Redheffer caused a sensation in Philadelphia when he announced a perpetual motion machine. Residents could view the device for a fee, he said, but none could approach it lest they damage the apparatus. When city commissioner Nathan Sellers arrived to observe the device, he happened to bring his son Coleman, who noticed something that all the adults had missed: The machine’s cogs were worn on the wrong side. The device that the machine was ostensibly driving was itself impelling the whole apparatus.

Redheffer decamped to New York City and tried again with an altered machine, but Robert Fulton noticed that this one ran unsteadily. He traced a catgut cord to an upper room, where an old man was turning a hand crank. Spectators destroyed the machine, and Redheffer fled the city.

Unquote

“Nothing, to my way of thinking, is better proof of a well-ordered mind than a man’s ability to stop just where he is and pass some time in his own company.” — Seneca, Letters From a Stoic

An Upper Stove

A problem by Soviet physicist Viktor Lange:

“By lifting up a bucket of coal to a third floor stove we increase the potential energy of the coal by about 800 J (the force of gravity on the coal is about 80 N and it is raised by about 10 m). Where will this additional potential energy go to when this coal is burnt in the stove?”

“If coal is burnt on the third floor height, the potential energy of the combustion products (water, ashes, carbon dioxide, carbon monoxide, and unburnt coal particles) will increase exactly as much as the coal potential energy.”

From Lange’s 1987 book Physical Paradoxes and Sophisms.

“Collective Farm”

In the best collective use,
Geese afoot are gaggles
(Even when one goose gets loose,
Falls behind and straggles);

Skein‘s the word for geese in flight.
Turtledoves form dools.
Barren‘s right (though impolite)
For a pack of mules.

Starlings join in murmuration,
Pheasants in a rye,
Larks in lovely exaltation,
Leopards, leap (they’re spry).

Ducks in flight are known as teams;
Paddings when they swim.
Herrings in poetic gleams
Please the wordsmith’s whim.

Cats collect into a clowder,
Kittens make a kindle.
Sloths of bears growl all the louder
As their forces dwindle.

Lapwings gather in deceit,
Apes convene in shrewdness,
Mares in stud (an odd conceit
Bordering on lewdness).

Foxes muster in a skulk,
Squirrels run in drays
While collectives in the bulk
Make up word bouquets.

— Felicia Lamport

An NSA Puzzle

A problem by National Security Agency mathematician Wendell W., from the agency’s March 2018 Puzzle Periodical:

Consider the following equations:

a2 × b × c2 × g = 5,100

a × b2 × e × f2 = 33,462

a × c2 × d3 = 17,150

a3 × b3 × c × d × e2 = 914,760

Find positive integers a, b, c, d, e, f, and g, all greater than 1, that satisfy all the equations.

If all four equations are satisfied, then multiplying all four equations together will produce another valid equation. We obtain:

a7 × b6 × c5 × d4 × e3 × f2 × g = 2,677,277,333,530,800,000.

The number on the right factors into prime powers as 2,677,277,333,530,800,000 = 27 × 36 × 55 × 74 × 113 × 132 × 17, as can be determined by trial division by the small primes 2, 3, 5, 7, 11, 13, and 17, for instance. So we have the new equation:

a7 × b6 × c5 × d4 × e3 × f2 × g = 27 × 36 × 55 × 74 × 113 × 132 × 17.

If p is any prime dividing a, then p7 divides the right hand side. Since only 2 appears to the seventh power, the only value p can take is 2. Since a must be greater than 1, we see that 2 must divide a. Because 2 appears to exactly the seventh power on the right, we see that a = 2. Canceling a7 on the left with 27 on the right leaves:

b6 × c5 × d4 × e3 × f2 × g = 36 × 55 × 74 × 113 × 132 × 17.

Repeating the same argument shows that b = 3, c = 5, d = 7, e = 11, f = 13, g = 17 is the unique solution to the new equation. However, it is still necessary that these values actually satisfy the original four equations, which in fact they do as can be checked easily. (To see why this last step is necessary, try using the same reasoning on the equations: x = 10, y2 = 9, z3 = 25, which clearly has no solutions in integers.)

In Brief

When H.P. Re of Coldwater, Mich., died in 1931, his claim to have the world’s shortest name was up for grabs, and the Associated Press held a sort of contest to find his successor. J. Ur of Torrington, Conn., expressed early confidence because he had no middle initial, but, AP reported:

C. Ek and J. Ek, brothers from Duluth, promptly entered the lists as cochampions. Mrs. V. Ek, not to be outdone, claimed not only the woman’s title, but the mixed doubles championship. A former Duluth policeman said his name was C. Sy.

Then Fairmount, Minnesota, entered E. Py, farmer; Clinton, Iowa, put forward C. Au, J. Au, and W. Au, triple threats; Indiana offered Ed Py, inmate of Newcastle Jail; and Indianapolis made a poor try with Fix Ax.

In the end the palm went to Aaron A of Chicago, who went by A.A., a name that AP noted “leads all others in the Chicago telephone directory, alphabetically as well as longitudinally.” A’s ancestors had been jewelers in Saxony, and a philologist speculated that the surname derived from an old German word for river.