John C. Baez's Blog, page 71

Twitter

I’m now going to try to announce all my new writings in one place: on Twitter.

Why? Well, someone I respect said he’s been following my online writings, off and on, ever since the old days of This Week’s Finds. He wishes it were easier to find my new stuff all in one place. Right now it’s spread out over several locations:

• Azimuth: serious posts on environmental issues and applied mathematics, fairly serious popularizations of diverse scientific subjects.

• Google+: short posts of all kinds...

Topological Crystals (Part 4)

Okay, let’s look at some examples of topological crystals. These are what got me excited in the first place. We’ll get some highly symmetrical crystals, often in higher-dimensional Euclidean spaces. The ‘triamond’, above, is a 3d example.

Review

First let me remind you how it works. We start with a connected graph 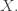This has a space 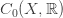of 0-chains, which are formal linear combinations of vertices, and a space 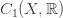of 1-chains, which are formal linear combinations of edges.

We choose a vertex in...

Topological Crystals (Part 3)

Last time I explained how to create the ‘maximal abelian cover’ of a connected graph. Now I’ll say more about a systematic procedure for embedding this into a vector space. That will give us a topological crystal, like the one above.

Some remarkably symmetrical patterns arise this way! For example, starting from this graph:

we get this:

Nature uses this pattern for crystals of graphene.

Starting from this graph:

we get this:

Nature uses this for crystals of diamond! Since the c...

Renewable Energy News

Some good news:

• Ed Crooks, Balance of power tilts from fossil fuels to renewable energy, Financial Times, 26 July 2016.

These are strange days in the energy business. Startling headlines are emerging from the sector that would have seemed impossible just a few years ago.

The Dubai Electricity and Water Authority said in May it had received bids to develop solar power projects that would deliver electricity costing less than three cents per kilowatt hour. This established a new worldwide l...

Topological Crystals (Part 2)

We’re building crystals, like diamonds, purely from topology. Last time I said how: you take a graph and embed its maximal abelian cover into the vector space 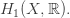Now let me say a bit more about the maximal abelian cover. It’s not nearly as famous as the universal cover, but it’s very nice.

First I’ll whiz though the basic idea, and then I’ll give the details.

The basic idea

By ‘space’ let me mean a connected topological space that’s locally nice. The basic idea is that if is some space, it...

Topological Crystals (Part 1)

A while back, we started talking about crystals:

• John Baez, Diamonds and triamonds, Azimuth, 11 April 2016.

In the comments on that post, a bunch of us worked on some puzzles connected to ‘topological crystallography’—a subject that blends graph theory, topology and mathematical crystallography. You can learn more about that subject here:

• Tosio Sunada, Crystals that nature might miss creating, Notices of the AMS 55 (2008), 208–215.

Greg Egan and I got so interested that we wrote a pa...

Frigatebirds

Frigatebirds are amazing!

They have the largest ratio of wing area to body weight of any bird. This lets them fly very long distances while only rarely flapping their wings. They often stay in the air for weeks at time. And one being tracked by satellite in the Indian Ocean stayed aloft for two months.

Surprisingly for sea birds, they don’t go into the water. Their feathers aren’t waterproof. They are true creatures of the air. They snatch fish from the ocean surface using their long, hoo...

Operads for “Systems of Systems”

“Systems of systems” is a fashionable buzzword for complicated systems that are themselves made of complicated systems, often of disparate sorts. They’re important in modern engineering, and it takes some thought to keep them from being unmanageable. Biology and ecology are full of systems of systems.

David Spivak has been working a lot on operads as a tool for describing systems of systems. Here’s a nice programmatic talk advocating this approach:

• David Spivak, Operads as a potential found...

Large Countable Ordinals (Part 3)

Last time we saw why it’s devilishly hard to give names to large countable ordinals.

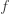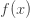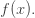An obvious strategy is to make up a function from ordinals to ordinals that grows really fast, so that is a lot bigger than the ordinal indexing it. This is indeed a good idea. But something funny tends to happen! Eventually catches up with In other words, you eventually hit a solution of

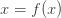
This is called a fixed point of 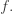At this point, there’s no way to use 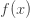as a name for unless you already have a name...

Large Countable Ordinals (Part 2)

Last time I took you on a road trip to infinity. We zipped past a bunch of countable ordinals

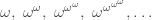
and stopped for gas at the first one after all these. It’s called Heuristically, you can imagine it like this:

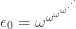
More rigorously, it’s the smallest ordinal obeying the equation

Beyond εo

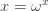
But I’m sure you have a question. What comes after ?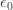

Well, duh! It’s

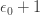
Then comes

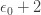
and then eventually we get to

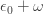
and then

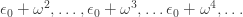
and after a long time

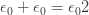
and then eventually

and then eventually….

Oh, I see! You wanted...