John C. Baez's Blog, page 70

Complex Adaptive System Design (Part 1)

In January of this year, I was contacted by a company called Metron Scientific Solutions. They asked if I’d like to join them in a project to use category theory to design and evaluate complex, adaptive systems of systems.

What’s a ‘system of systems’?

It’s a system made of many disparate parts, each of which is a complex system in its own right. The biosphere is a system of systems. But so far, people usually use this buzzword for large human-engineered systems where the different components...

Struggles with the Continuum (Part 8)

We’ve been looking at how the continuum nature of spacetime poses problems for our favorite theories of physics—problems with infinities. Last time we saw a great example: general relativity predicts the existence of singularities, like black holes and the Big Bang. I explained exactly what these singularities really are. They’re not points or regions of spacetime! They’re more like ways for a particle to ‘fall off the edge of spacetime’. Technically, they are incomplete timelike or null geod...

Struggles with the Continuum (Part 7)

Combining electromagnetism with relativity and quantum mechanics led to QED. Last time we saw the immense struggles with the continuum this caused. But combining gravity with relativity led Einstein to something equally remarkable: general relativity.

Gravitational lensing by a non-rotating black hole

In general relativity, infinities coming from the continuum nature of spacetime are deeply connected to its most dramatic successful predictions: black holes and the Big Bang. In this theory,...

Struggles with the Continuum (Part 6)

Last time I sketched how physicists use quantum electrodynamics, or ‘QED’, to compute answers to physics problems as power series in the fine structure constant, which is

I concluded with a famous example: the magnetic moment of the electron. With a truly heroic computation, physicists have used QED to compute this quantity up to order 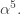If we also take other Standard Model effects into account we get agreement to roughly one part in

However, if we continue adding up terms in this power ser...

Struggles with the Continuum (Part 5)

Quantum field theory is the best method we have for describing particles and forces in a way that takes both quantum mechanics and special relativity into account. It makes many wonderfully accurate predictions. And yet, it has embroiled physics in some remarkable problems: struggles with infinities!

I want to sketch some of the key issues in the case of quantum electrodynamics, or ‘QED’. The history of QED has been nicely told here:

⢠Silvian Schweber, QED and the Men who Made it: Dyson, Fe...

The Circular Electron Positron Collider

Chen-Ning Yang is perhaps China’s most famous particle physicists. Together with Tsung-Dao Lee, he won the Nobel prize in 1957 for discovering that the laws of physics known the difference between left and right. He helped create Yang–Mills theory: the theory that describes all the forces in nature except gravity. He helped find the Yang–Baxter equation, which describes what particles do when they move around on a thin sheet of matter, tracing out braids.

Right now the world of particle physi...

Struggles with the Continuum (Part 4)

In this series we’re looking at mathematical problems that arise in physics due to treating spacetime as a continuum—basically, problems with infinities.

In Part 1 we looked at classical point particles interacting gravitationally. We saw they could convert an infinite amount of potential energy into kinetic energy in a finite time! Then we switched to electromagnetism, and went a bit beyond traditional Newtonian mechanics: in Part 2 we threw quantum mechanics into the mix, and in Part 3 we t...

Struggles with the Continuum (Part 3)

In these posts, we’re seeing how our favorite theories of physics deal with the idea that space and time are a continuum, with points described as lists of real numbers. We’re not asking if this idea is true: there’s no clinching evidence to answer that question, so it’s too easy to let ones philosophical prejudices choose the answer. Instead, we’re looking to see what problems this idea causes, and how physicisists have struggled to solve them.

We started with the Newtonian mechanics of poin...

Struggles with the Continuum (Part 2)

Last time we saw that that nobody yet knows if Newtonian gravity, applied to point particles, truly succeeds in predicting the future. To be precise: for four or more particles, nobody has proved that almost all initial conditions give a well-defined solution for all times!

The problem is related to the continuum nature of space: as particles get arbitrarily close to other, an infinite amount of potential energy can be converted to kinetic energy in a finite amount of time.

I left off by aski...

Struggles with the Continuum (Part 1)

Is spacetime really a continuum? That is, can points of spacetime really be described—at least locally—by lists of four real numbers 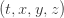? Or is this description, though immensely successful so far, just an approximation that breaks down at short distances?

Rather than trying to answer this hard question, let’s look back at the struggles with the continuum that mathematicians and physicists have had so far.

The worries go back at least to Zeno. Among other things, he argued that that an arrow can...